§170 正項級数の積
ディリクレの定理から次の系が直ちに得られる:
\(u_{0} + u_{1} + u_{2} + \cdots\) と \(v_{0} + v_{1} + v_{2} + \cdots\) が収束する正項級数で和が \(s,\ t\) なら、級数 \[ u_{0} v_{0} + (u_{1} v_{0} + u_{0} v_{1}) + (u_{2} v_{0} + u_{1} v_{1} + u_{0} v_{2}) + \cdots \] は収束し、その和は \(st\) である。
\(u_{m}v_{n}\) の積を全て並べた二次元の無限配列
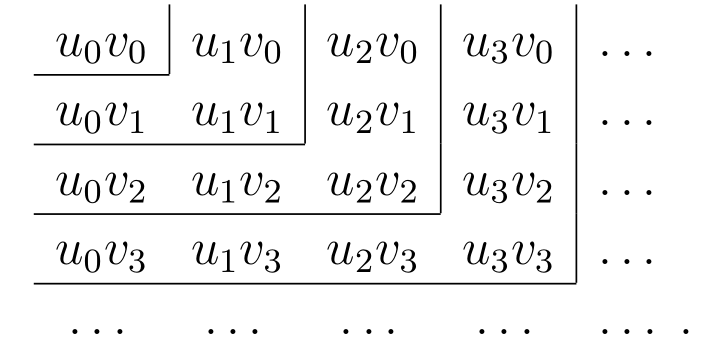
を考える。この配列を並べ替えて得られる通常の無限級数は無数にあるが、それらのうち次の二つに注目する:
-
\(m + n = 0\) となる唯一の項 \(u_{0}v_{0}\) を最初に取り、次に \(m + n = 1\) となる二つの項 \(u_{1}v_{0},\ u_{0}v_{1}\) を取る。次は \(m + n = 2\) となる三つの項 \(u_{2}v_{0},\ u_{1}v_{1},\ u_{0}v_{2}\) と以降同様に取る。こうして得られる級数 \[ u_{0}v_{0} + (u_{1}v_{0} + u_{0}v_{1}) + (u_{2}v_{0} + u_{1}v_{1} + u_{0}v_{2}) + \cdots \] は今考えている級数である。
-
添え字が \(0\) だけからなる \(u_{0}v_{0}\) を最初に取り、次に添え字が \(1\) を含み \(1\) より大きい数字を含まない項 \(u_{1}v_{0},\ u_{1}v_{1},\ u_{0}v_{1}\) を取る。次は添え字が \(2\) を含み \(2\) より大きい数字を含まない項 \(u_{2}v_{0},\ u_{2}v_{1},\ u_{2}v_{2},\ u_{1}v_{2},\ u_{0}v_{2}\) と以降同様に取る。こういったグループの和はそれぞれ \[ \begin{gathered} u_{0}v_{0},\quad (u_{0} + u_{1})(v_{0} + v_{1}) - u_{0}v_{0},\\ (u_{0} + u_{1} + u_{2})(v_{0} + v_{1} + v_{2}) - (u_{0} + u_{1})(v_{0} + v_{1}), \cdots \end{gathered} \] であり、最初の \(n + 1\) グループの和は \[ (u_{0} + u_{1} + \cdots + u_{n})(v_{0} + v_{1} + \cdots + v_{n}) \] となる。よってこの和は \(n \to \infty\) で \(st\) に向かう。なおこうして級数の和を求めると、一つ目・二つ目・三つ目 \(\cdots\) のグループの和は上図の一つ目・二つ目・三つ目 \(\cdots\) の四角形の内側にある項の和に対応する。
このように形成される級数の和は \(st\) である。ここで一つ目の級数は二つ目の級数の順序を入れ替えたものだから、ディリクレの定理より、\(st\) に収束する。よって示すべき事実が証明された。
-
\(r \lt 1\) で次の等式が成り立つことを確認せよ: \[ 1 + r^{2} + r + r^{4} + r^{6} + r^{3} + \cdots = 1 + r + r^{3} + r^{2} + r^{5} + r^{7} + \cdots = \frac{1}{1 - r} \]
-
級数1 \(u_{0} + u_{1} + \cdots\) と \(v_{0} + v_{1} + \cdots\) のどちらかが発散するなら、\(u_{0}v_{0} + (u_{1}v_{0} + u_{0}v_{1}) + (u_{2}v_{0} + u_{1}v_{1} + u_{0}v_{2}) + \cdots\) も発散する。ただし片方の級数が全て \(0\) となる場合は除く。
-
三つの級数 \(u_{0} + u_{1} + \cdots,\ v_{0} + v_{1} + \cdots,\ w_{0} + w_{1} + \cdots\) がそれぞれ \(r,\ s,\ t\) に収束するなら、\(\lambda_{k} = \sum u_{m}v_{n}w_{p}\) としたときの級数 \(\sum \lambda_{k}\) は \(rst\) に収束する。ただし総和は \(m + n + p = k\) となる全ての \(m,\ n,\ p\) に対して取る。
-
\(\sum u_{n}\) と \(\sum v_{n}\) が \(s\) と \(t\) に収束するなら、\(w_{n} = \sum u_{l} v_{m}\) としたときの級数 \(\sum w_{n}\) は \(st\) に収束する。ただし総和は \(lm = n\) となる \(l,\ m\) に対して取る。
-
問題 2–4 ではこれまでと同じように正項級数を考える。[return]