§22 極座標

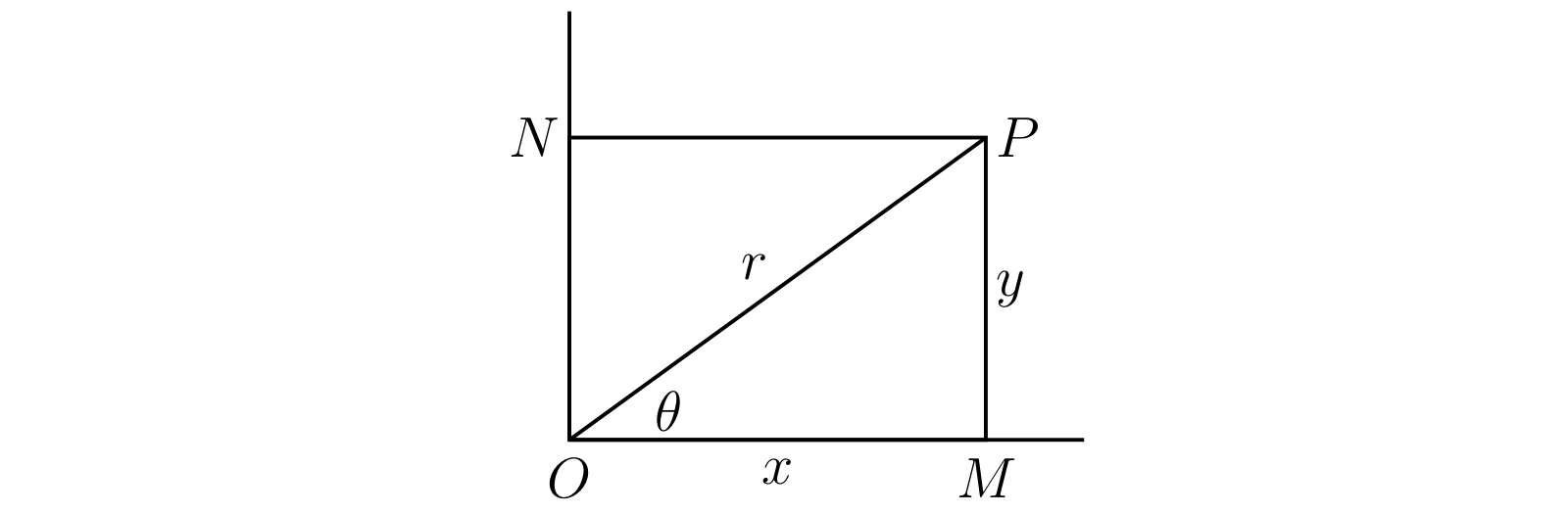
前節では \(P\) の座標の大きさ \(OM = x\) と \(MP = y\) で \(P\) の位置を特定した。\(OP = r\) および \(\angle MOP = \theta\) として、\(\theta\) は (正の方向に測って) \(0\) から \(2\pi\) だとする。このとき \[ \begin{aligned} x & = r\cos\theta, \quad y & = r\sin\theta, \quad r & = \sqrt{x^{2} + y^{2}}, \quad \cos\theta : \sin\theta : 1 & = x : y : r \end{aligned} \] が成り立ち、\(r\) と \(\theta\) からも \(P\) の位置を決定できると分かる。加えて\(r\) は必ず \(0\) 以上となる¹。

\(P\) がとある軌跡上を動くなら、\(r\) と \(\theta\) の間には関係が生まれる。これを \(r = f(\theta)\) あるいは \(\theta = F(r)\) と表記し、軌跡の極方程式 (polar equation) と呼ぶ。上記の関係を使えば極方程式を \((x, y)\) の方程式から求められる (逆もできる)。

例えば直線の極方程式は次の形をしていると示せる: \[ r\cos(\theta - \alpha) = p \] ここで \(p\) と \(\alpha\) は定数である。また方程式 \(r = 2a\cos\theta\) は原点を通る円を表す。この方程式は定数 \(A,\ c,\ \alpha\) を使った \[ r^{2} + c^{2} - 2rc\cos(\theta - \alpha) = A^{2} \] から得られる。

1. 極座標は \(r\) が正でも負でもあり得るように定義されることもある。こうすると二つの座標 —例えば \((1, 0)\) と \((-1, \pi)\)— が同じ点を表す。二つの座標系の違いは \(l \gt 0\) と \(e \gt 1\) を使った方程式 \(l/r = 1 - e\cos\theta\) を考えると明らかになる。私たちの定義では \(r\) は正なので \(\cos\theta \lt 1/e\) が成り立ち、方程式は双曲線の一方の枝だけを表す。一方で負の \(r\) を許す座標系なら \(-l/r = 1 - e\cos\theta\) も含まれるので、双曲線全体が表される。^[return]