§5 無理数 (その 3)
前節では正の有理数を二つのクラス と に分割した。このとき (i) の全ての要素は のどんな要素よりもより大きく、(ii) の要素と の要素の組であって差が好きなだけ小さいものを取ることができ、(iii) は最大要素を持たず、 は最小要素を持たない。直線の常識的な性質や初等幾何と初等代数からの要請といったものを考えると、 の全ての要素よりも大きく の全ての要素よりも小さい数 、および に対応する点と に対応する点を分ける 上の点 の存在が必要となる。
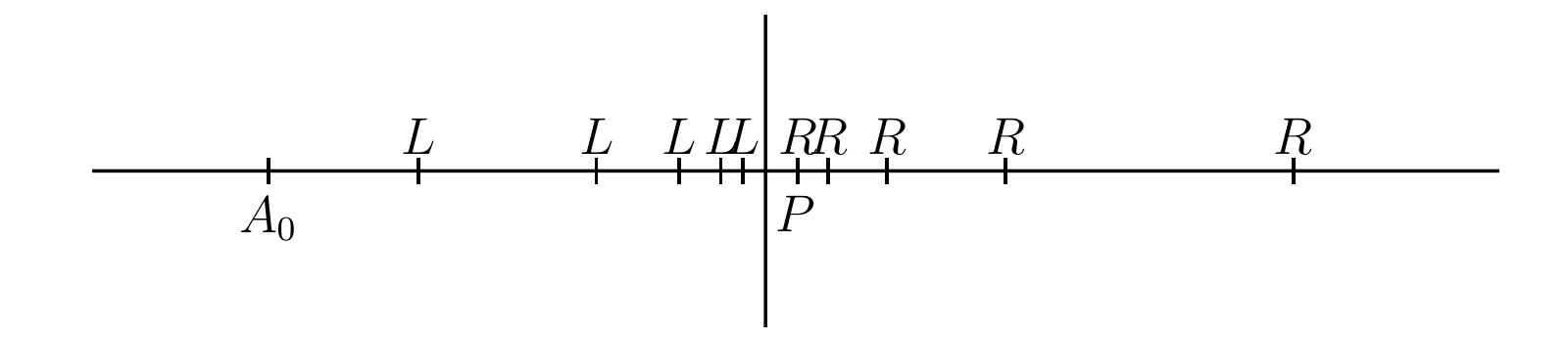
そのような数 が存在して代数法則に従うと一時的に仮定する。この仮定の下では例えば が明確な意味を持ち、 は とちょうど等しい。もし が よりも小さいとすると、前節の議論から有理数 であって が と の間にあるものが存在する、つまり よりも大きい の要素を見つけられるが、これは が と の要素を分けるという仮定と矛盾する。したがって は より小さくなりえず、同様に よりも大きくなりえない。よって と結論でき、代数ではこの数 を と表記する。二乗して になる有理数は存在しないので、もちろん は有理数でない。 は無理数 (irrational number) の一番単純な例である。
以上の議論は 以外の方程式にもそのまま適用できる。例えば完全平方数でない自然数 についての 、あるいは といった方程式、さらに後述するように のような方程式にも適用できる。そのためこういった方程式を満たす無理数 やそれに対応する 上の点 の存在も私たちは信じることになる。こういった長さは ( と違って) 初等幾何学の方法で構成できないにもかかわらずである。
知っての通り、初等代数では という方程式の根を あるいは と表記する。さらに という式は という意味を持つ。こういった定義から「指数法則 (laws of indices)」 が と が有理数の場合へと拡張される。
読者は他の講義も受けているかもしれない。もし望むなら、 や といった「無理数」が存在して、読者もよく知っているであろう代数法則も成り立つものだと仮定してしまってもよい1。もしそうするなら、次の節からの抽象的な議論を飛ばして §13 まで進んで構わない。
一方でそのような素朴な態度を取る気にならないのであれば、こういった問題をより詳しく議論する以降の節を注意深く読むよう強く勧める2。
-
§4 で の近似値として示した小数の二乗と の差を求めよ。
-
次の有理数の二乗と の差を求めよ:
-
が の良い近似なら は のより良い近似であること、そして二つの値の誤差の方向が逆であることを示せ。この結果を用いて前問の近似値の列を延長せよ。
-
と が の近似値で、それぞれ下からの近似値と上からの近似値とする。このとき かつ なら が成り立つ。
-
方程式 は のとき満たされる。これまでの節の議論をどこまでこの方程式に当てはめられるか調べよ (全ての を に書き換える)。 [クラス と を同様に定義すると、この二つのクラスは全ての有理数を含まない。有理数 の二乗は より小さくもなければ大きくもないので、有理数 が例外となる]