第九章 実数変数に対する対数関数と指数関数

§196 対数関数

これまでの章で考えた本質的に異なる関数の数というのはそれほど多くない。ここまでに登場した普通の用途で最も重要な関数をあげれば、多項式・有理関数・陽な代数関数・陰な代数関数・三角関数・三角関数の逆関数となる。

しかし数学で重要な関数がこれで全て揃ったとはとても言えない。数学的な知識の範囲は、新しい関数のクラスを一つずつ解析の対象に加えること段階的に拡張されてきた。新しい関数が対象に加わる一般的な理由は、そのとき数学者の注意を引いていた問題がそれまでに知られていた関数では解けないように思えるためである。この考え方は無理数や複素数を最初に導入した議論とよく似ている。こういった数はとある代数方程式がそれまでに認識されていた数では解けなかったために定義されていた。新しい関数を最も数多く生み出している問題の一つが積分であり、次のようにして新しい関数が導入される: とある関数 \(f(x)\) の積分をこれまでに知られた関数を使って計算する試みがなされるも、全て失敗する。失敗が何度も繰り返されるにつれ、積分が解けない可能性が現実性を帯びてくる。ときには解けないことが証明されることもあるが、一般的に言ってそういった命題の厳密な証明はもっと後になってから表れる。普通は数学者が十分に納得した段階でその積分は解けないものだとみなし、新しい関数 \(F(x)\) をその性質 \(F'(x) = f(x)\) で定義してしまう。数学者はこの定義からはじめて \(F(x)\) の様々な性質を調べ、その結果として \(F(x)\) には既知の関数を有限回組み合わせた関数が持たない性質を持っていることが判明し、最初の積分の問題がどうやっても解けないという仮定が正当化される。この本にもこういった関数は現れている。第六章では次の等式を使って関数 \(\log x\) を定義した: \[ \log x = \int \frac{dx}{x} \]

§197 対数関数の定義

\(x\) の対数 \(\log x\) は次の等式で定義される: \[ \log x = \int_{1}^{x} \frac{dt}{t} \] 例 76.2 からは積分範囲が \(x = 0\) を含むときこの積分が意味を持たないと分かるので、\(x\) は正である必要がある。積分の下端は \(1\) でなくても構わないが、\(1\) とすれば \(\log 1 = 0\) となるので都合がいい。

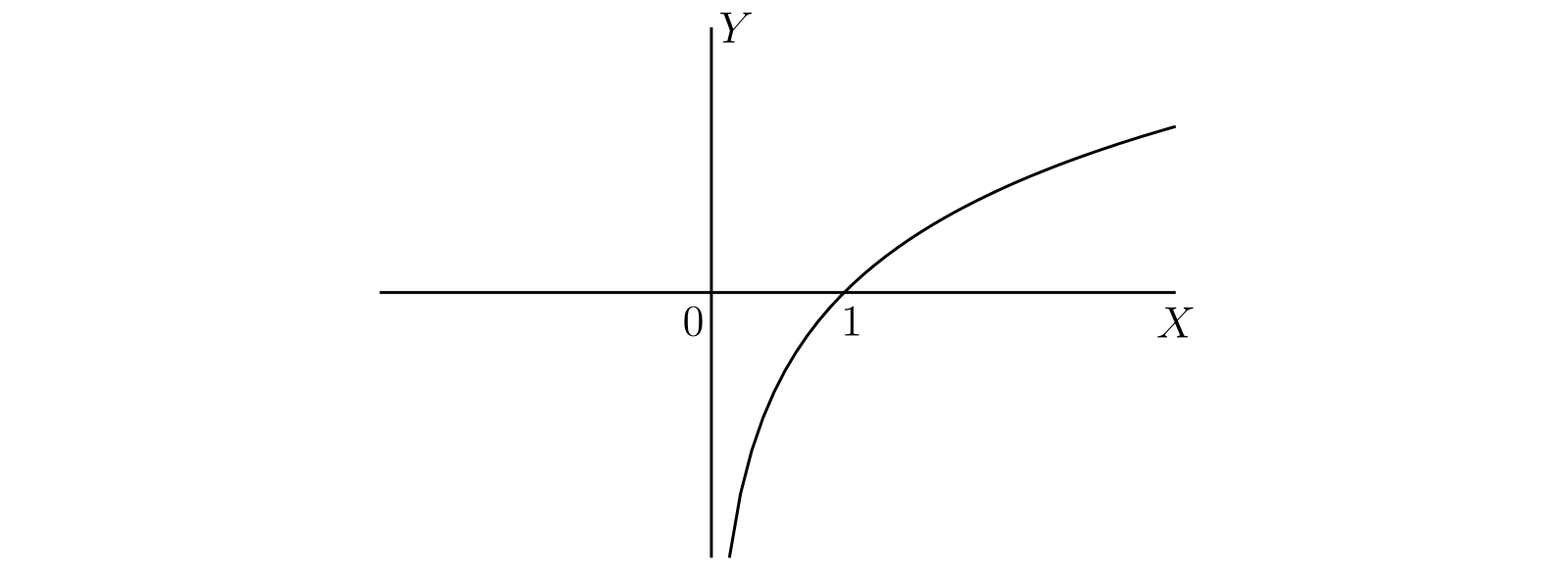
では \(x\) が \(0\) から \(\infty\) まで変化するときの \(\log x\) の振る舞いを考えよう。\(\log x\) が \(x\) の連続関数であり、\(x\) に関して単調増加であり、次の導関数を持つことが定義から直ちに従う: \[ D_{x} \log x = \frac{1}{x} \] さらに §175 から \(x \to \infty\) のとき \(\log x\) が \(\infty\) に向かうと分かる。

\(x\) が \(1\) より小さい正の実数のとき \(\log x\) は負となる。これは \[ \log x = \int_{1}^{x} \frac{dt}{t} = -\int_{x}^{1} \frac{dt}{t} \lt 0 \] から従う。さらにこの積分で \(t = 1/u\) と置換すると \[ \log x = \int_{1}^{x} \frac{dt}{t} = -\int_{1}^{1/x} \frac{du}{u} = -\log \dfrac{1}{x} \] を得る。つまり \(x\) が \(1\) から \(0\) へ減少するとき \(\log x\) は単調に \(-\infty\) へ向かう。

対数関数のグラフの概形を 図 52 に示す。\(\log x\) の導関数は \(1/x\) だから、曲線の傾きは \(x\) が大きいとき非常になだらかで、\(x\) が小さいとき非常に急になる。

§198 \(\log x\) が満たす関数方程式

\(\log x\) は次の関数方程式を満たす: \[ f(xy) = f(x) + f(y) \qquad \text{(1)} \] 置換 \(t = yu\) を使うと \[ \begin{aligned} \log xy & = \int_{1}^{xy} \frac{dt}{t} = \int_{1/y}^{x} \frac{du}{u} = \int_{1}^{x} \frac{du}{u} - \int_{1}^{1/y} \frac{du}{u}\\ & = \log x - \log \dfrac{1}{y} = \log x + \log y \end{aligned} \] となり、この関係が証明される。

§199 \(\log x\) が無限大に向かうときの振る舞い

例 36.6 で \(x\) の関数が \(x\) と共に無限大に向かうときの向かい方を定義した。\(x\) が大きいときに一次・二次・三次 \(\cdots\) の大きさを持つ関数を区別し、\(x \to \infty\) で \(f(x)/x^{k}\) が \(0\) でない極限に向かうとき \(f(x)\) は \(k\) 次の大きさを持つと定めた。

\(x\) と共に無限大に向かう関数で一次より小さい大きさを持つ関数を定義するのは難しくない。例えば \(\sqrt{x},\ \sqrt[3]{x},\ \sqrt[4]{x},\ \ldots\) は全て一次より小さい大きさを持つ。有理数 \(\alpha\) に対しても \(x^{\alpha}\) が \(\alpha\) 次の大きさを持つと言うことにすると、好きなだけ小さい \(\alpha\) に対する大きさが定義される。例えば \(.0000001\) 次の大きさが存在する。これを持って \(f(x)\) の "大きさの次元" は有理数の \(\alpha\) で全てを表せると考えるかもしれない。つまり \(x\) と共に無限大に向かう任意の \(f(x)\) に対して、\(x^{\alpha}\) が \(f(x)\) よりゆっくりと無限大に向かう有理数 \(\alpha\) および \(x^{\beta}\) が \(f(x)\) よりも速く無限大に向かう有理数 \(\beta\) が存在すると思っても不思議ではない。

\(\log x\) の特徴でおそらく最も興味深いのが、\(x\) が無限大に向かうときの振る舞いである。この特徴によると、上述の非常に自然に見える命題は成り立たない。つまり\(\bm{\log x}\) は \(\bm{x}\) と共に無限大に向かうが、その速度は \(\bm{x}\) の任意の (整数および有理数の) 正のべきより遅い。言い換えると、\(\log x \to \infty\) だが \[ \frac{\log x}{x^{\alpha}} \to 0 \] が全ての \(\alpha\) で成り立つ。この事実は「\(\log x\) の無限大の次元は無限に小さい」とくだけて表現されることもあるが、ここまで読み進めた読者に対してこの言い回しの意味を注意する必要はほとんどないだろう。

§200 \(\log x\) の無限大の次元が小さいことの証明

\(\beta\) を任意の正の実数とすると、\(t \gt 1\) に対して \(\dfrac{1}{t} \lt \dfrac{1}{t^{1-\beta}}\) が成り立つ。よって \[ \log x = \int_{1}^{x} \frac{dt}{t} \lt \int_{1}^{x} \frac{dt}{t^{1-\beta}} \] であり、ここから \(x \gt 1\) なら \[ \log x \lt \frac{x^{\beta} - 1}{\beta} \lt \frac{x^{\beta}}{\beta} \] だと分かる。\(\alpha\) を任意の正の実数とすれば、\(\alpha\) より小さい \(\beta\) に対して \[ 0 \lt \frac{\log x}{x^{\alpha}} \lt \frac{x^{\beta-\alpha}}{\beta} \quad (x \gt 1) \] となる。一方で \(\alpha \gt \beta\) より \(x \to \infty\) のとき \(\dfrac{x^{\beta-\alpha}}{\beta} \to 0\) だから、 \[ \frac{\log x}{x^{\alpha}} \to 0 \] が得られる。

§201 \(x \to +0\) における \(\log x\) の振る舞い

\(x = \dfrac{1}{y}\) なら \[ \dfrac{\log x}{x^{\alpha}} = -y^{\alpha} \log y \] が成り立つから、前節の結果より \[ \lim_{y\to +0} y^{\alpha} \log y = -\lim_{x\to +\infty} \frac{\log x}{x^{\alpha}} = 0 \] を得る。つまり \(x\) が正の値を取りながら \(0\) に近づくとき \(\log x\) は \(-\infty\) に、\(\log(1/x) = -\log x\) は \(\infty\) に向かうが、\(\log(1/x)\) が \(\infty\) に向かう速度は \(1/x\) の (整数および有理数の) どんなべきよりも遅い。

§202 無限大の大きさの尺度としての対数

関数の列 \[ x,\quad \sqrt{x},\quad \sqrt[3]{x},\ \ldots,\quad \sqrt[n]{x},\ \ldots \] をもう一度考える。この列に含まれる二つの関数を \(f(x)\) と \(\phi(x)\) とすれば、\(x \to \infty\) のとき \(f(x)\) と \(\phi(x)\) は両方とも \(\infty\) に向かい、\(f(x)/\phi(x)\) は \(f(x)\) が \(\phi(x)\) の右にあるなら \(0\) に、\(\phi(x)\) の左にあるなら \(\infty\) に向かう。ここまでの結果を使えば、 上に書かれた列の左に新しい項を追加できると分かる。最初に追加されるのは \(\log x\) であり、この関数は最初からある項のどれよりも遅く無限大に向かう。次が \(\log x\) よりも遅く \(\infty\) に向かう \(\sqrt{\log x}\) であり、さらにその次に \(\sqrt{\log x}\) よりも遅い \(\sqrt[3]{\log x}\) と続く。こうして次の列が得られる: \[ x,\quad \sqrt{x},\quad \sqrt[3]{x},\quad \ldots, \quad \sqrt[n]{x},\quad \ldots, \quad \log x,\quad \sqrt{\log x},\quad \sqrt[3]{\log x},\quad \ldots, \quad \sqrt[n]{\log x},\quad \ldots \] この列は無限の列が二つ並んでいるだけだが、これで終わりではない。\(\log x\) の対数を取った関数 \(\log\log x\) を考える。任意の正の \(\alpha\) で \((\log x)/x^{\alpha} \to 0\) だから、\(x = \log y\) とすると \[ \frac{\log\log y}{(\log y)^{\alpha}} = \frac{\log x}{x^{\alpha}} \to 0 \] を得る。つまり \(\log\log y\) は \(y\) と共に無限大に向かうが、その速度は \(\log y\) の任意のべきより遅い。よってこの列を \[ \begin{gathered} x,\quad \sqrt{x},\quad \sqrt[3]{x},\quad \ldots,\qquad \log x,\quad \sqrt{\log x},\quad \sqrt[3]{\log x},\quad \ldots,\\ \log\log x,\quad \sqrt{\log\log x},\quad \ldots,\quad \sqrt[n]{\log\log x},\quad \ldots \end{gathered} \] とさらに延長できる。\(\log\log\log x,\ \log\log\log\log x,\ \ldots\) を使えばこの列をさらに好きなだけ伸ばせるのも明らかだろう。また \(x = 1/y\) とすれば、\(y\) が正の値を取りながら \(0\) に向かうときに \(\infty\) に向かう関数で異なる無限大の尺度を持つものが得られる²。

§203 実数 \(e\)

ここでとある実数を新しく定義する。通常 \(e\) で表されるこの実数は高等数学において途方もなく重要であり、\(\pi\) と同じように解析学の基礎的な定数の一つである。

\(e\) を対数が \(\bm{1}\) となる実数と定義する。違う表現を使うと、\(e\) は \[ 1 = \int_{1}^{e} \frac{dt}{t} \] という等式で定義される。\(\log x\) は (§95 の意味で) \(x\) の狭義単調増加関数だから、値 \(1\) を一度しか取らない。よってこの定義は一つの実数を確かに定義する。

ここで \(\log xy = \log x + \log y\) から \[ \log x^{2} = 2\log x,\quad \log x^{3} = 3\log x,\ \ldots,\quad \log x^{n} = n\log x \] が全ての正の整数 \(n\) に対して成り立つと分かる。よって \[ \log e^{n} = n\log e = n \] となる。また \(p,\ q\) を正の整数とすれば、\(e^{p/q}\) は \(e^{p}\) の \(q\) 乗根を表す。そして \[ p = \log e^{p} = \log(e^{p/q})^{q} = q\log e^{p/q} \] より \(\log e^{p/q} = p/q\) が分かる。よって正の有理数 \(y\) に対して \(e^{y}\) で \(e\) の \(y\) 次のべきを表すとすれば \[ \log e^{y} = y \qquad \text{(1)} \] となる。さらに \(\log e^{-y} = -\log e^{y} = -y\) が成り立つから、等式 \(\text{(1)}\) は正負を問わず全ての有理数 \(y\) に対して成り立つ。これを言い換えれば、二つの等式 \[ y = \log x,\quad x = e^{y} \qquad \text{(2)} \] は片方からもう一方を導ける。ただし \(y\) は有理数で、\(e^{y}\) は正とする。今の段階では指数が無理数のべき \(e^{y}\) を定義していないので、\(e^{y}\) は有理数の \(y\) に対してだけ定義される。

§204 指数関数の定義

続いて全ての実数 \(y\) に対する指数関数 (exponential function) \(e^{y}\) を対数関数の逆関数として定義する。つまり \(y = \log x\) のとき \[ x = e^{y} \] と書く。

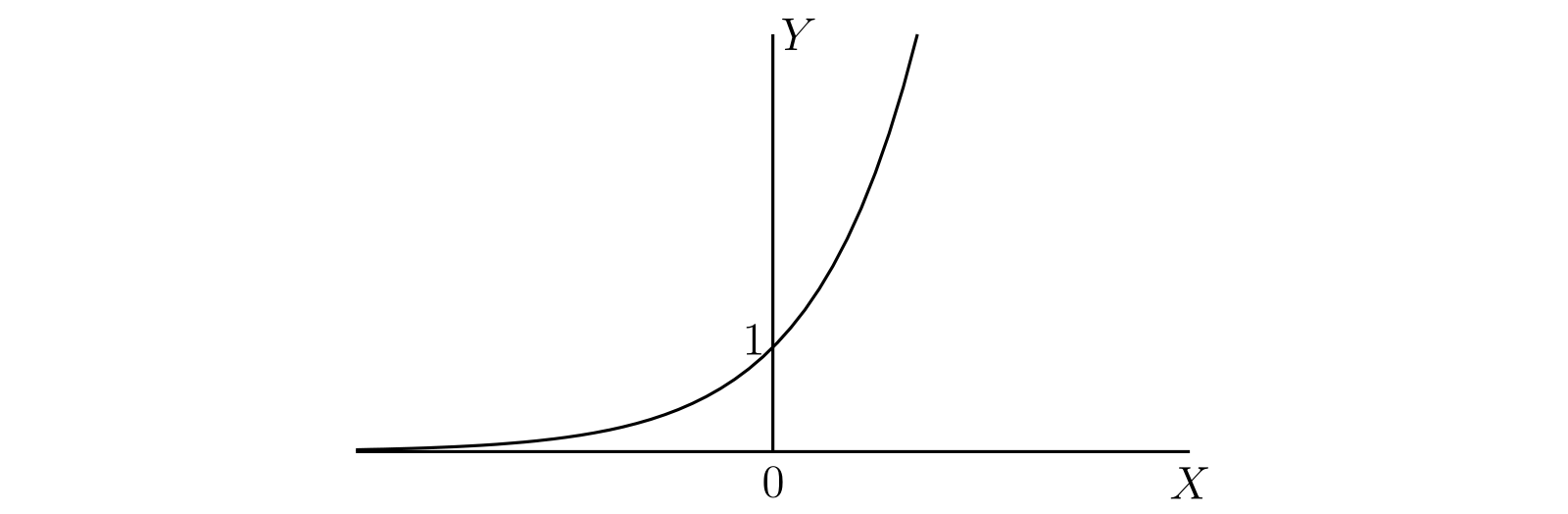
前に見たように、\(x\) が \(0\) から \(\infty\) に向かって変化すると \(y\) は \(-\infty\) から \(\infty\) へ狭義に単調増加する。よって一つの \(y\) の値には一つの \(x\) の値が対応し、その逆も成り立つ。同様に \(y\) は \(x\) の連続関数であり、§109 から \(x\) が \(y\) の連続関数だと分かる。

したがって \(e^{y}\) は \(y\) に関して連続で常に正な関数で、\(y\) が \(-\infty\) から \(\infty\) に変化するとき \(0\) から \(\infty\) へ単調に増加する。さらに \(y\) が有理数なら、\(e^{y}\) は \(e\) の初等的な意味での \(y\) 次の正のべきと等しくなる。\(e^{y}\) のグラフの概形を 図 53 に示す。

§205 指数関数の特徴 (その 1)

1. \(x = e^{y}\) なら \(y = \log x\) であり、このとき \(dy/dx = 1/x\) が成り立つ。ここから \[ \frac{dx}{dy} = x = e^{y} \] を得る。つまり指数関数の導関数は指数関数に等しい。より一般には \(x = e^{ay}\) なら \(dx/dy = ae^{ay}\) となる。

2. 指数関数は次の関数方程式を満たす: \[ f(y + z) = f(y)f(z) \]

   \(y\) と \(z\) が有理数なら、この等式は初等的な指数法則から従う。\(y\) と \(z\) の片方または両方が無理数なら、\(\lim y_{n} = y\) および \(\lim z_{n} = z\) を満たす二つの有理数列 \(y_{1},\ y_{2},\ \ldots,\ y_{n},\ \ldots\) と \(z_{1},\ z_{2},\ \ldots,\ z_{n},\ \ldots\) を考えると、指数関数は連続だから \[ e^{y} × e^{z} = \lim e^{y_{n}} × \lim e^{z_{n}} = \lim e^{y_{n}+z_{n}} = e^{y+z} \] を得る。特に \(e^{y} × e^{-y} = e^{0} = 1\) つまり \(e^{-y} = 1/e^{y}\) が成り立つ。

   あるいは \(\log x\) が満たす関数方程式から \(e^{y}\) が満たす関数方程式を導くこともできる。\(y_{1} = \log x_{1},\ y_{2} = \log x_{2}\) なら \(x_{1} = e^{y_{1}},\ x_{2} = e^{y_{2}}\) であり、\(y_{1} + y_{2} = \log x_{1} + \log x_{2} = \log x_{1}x_{2}\) から次を得る: \[ e^{y_{1}+y_{2}} = e^{\log x_{1}x_{2}} = x_{1}x_{2} = e^{y_{1}} × e^{y_{2}} \]

§206 指数関数の特徴 (その 2)

3. \(y\) が無限大に向かうときに \(e^{y}\) が無限大に向かう速度は \(y\) のどんなべきよりも速い。つまり \(y \to \infty\) のとき \[ \lim \frac{y^{\alpha}}{e^{y}} = \lim e^{-y}y^{\alpha} = 0 \] がどんなに大きい \(\alpha\) に対しても成り立つ。

   任意に小さい正の有理数 \(\beta\) に対して \(x \to \infty\) で \((\log x)/x^{\beta} \to 0\) だと前に見たので、\(\alpha = 1/\beta\) とすれば任意に大きい \(\beta\) に対して \((\log x)^{\alpha}/x \to 0\) が分かり、\(x = e^{y}\) とすれば上の式を得る。また \(e^{\gamma y}\) は \(\gamma \gt 0\) なら \(\infty\) に、\(\gamma \lt 0\) なら \(0\) に向かい、いずれの場合でもその速度は \(y\) の任意のべきより速い。

§207 一般の指数 \(a^{x}\)

関数 \(a^{x}\) は \(a = e\) の場合を除いて有理数の \(x\) に対してしか定義されていない。ここで \(a\) が任意の正の実数である場合を考える。\(x\) を正の有理数 \(p/q\) として、\(y\) が \(y^{q} = a^{p}\) で与えられる \(a^{p/q}\) を表すとする。ここから \[ q\log y = p\log a,\quad \log y = \frac{p}{q}\log a = x\log a \] が分かるので、 \[ y = e^{x\log a} \] が成り立つ。この等式を無理数 \(x\) に対する \(a^{x}\) の定義として採用する。例えば \(10^{\sqrt{2}} = e^{\sqrt{2}\log 10}\) である。また無理数 \(x\) に対する \(a^{x}\) は正の \(a\) に対してしか定義されず、\(a^{x}\) は正の値を取り、\(\log a^{x} = x\log a\) を満たすことが確認できる。\(a^{x}\) の最も重要な性質を次に示す。

1. \(a\) がどんな値でも \(a^{x} × a^{y} = a^{x+y}\) と \((a^{x})^{y} = a^{xy}\) が成り立つ。つまり指数法則は有理数だけではなく無理数に対しても成り立つ。証明は指数関数の性質を使って \[ a^{x} × a^{y} = e^{x\log a} × e^{y\log a} = e^{(x+y)\log a} = a^{x+y} \] \[ (a^{x})^{y} = e^{y\log a^{x}} = e^{xy\log a} = a^{xy} \] と変形する。

2. \(a \gt 1\) なら正の \(\alpha\) が存在して \(a^{x} = e^{x\log a} = e^{\alpha x}\) が成り立つ。つまり \(a^{x}\) のグラフは \(e^{x}\) のグラフと相似となる。さらに \(x \to \infty\) で \(a^{x} \to \infty\) であり、その速度は \(x\) の任意のべきよりも速い。

   \(a \lt 1\) なら正の \(\beta\) が存在して \(a^{x} = e^{x\log a} = e^{-\beta x}\) が成り立つ。つまり \(a^{x}\) のグラフは \(e^{x}\) のグラフと相似だが、左右が反転する。さらに \(x \to \infty\) で \(a^{x} \to 0\) であり、その速度は \(1/x\) の任意のべきより早い。

3. \(a^{x}\) は \(x\) に関して連続で次が成り立つ: \[ D_{x} a^{x} = D_{x} e^{x\log a} = e^{x\log a} \log a = a^{x} \log a \]

4. \(a^{x}\) は \(a\) に関しても連続で次が成り立つ: \[ D_{a} a^{x} = D_{a} e^{x\log a} = e^{x\log a} \frac{x}{a} = xa^{x-1} \]

5. \(x \to 0\) のとき \((a^{x} - 1)/x \to \log a\) が成り立つ。当然これは \(D_{x}a^{x} = a^{x}\log a\) という結果の系に過ぎないが、このように表現しておくと便利な場合がある。また 例 85.3 の \(x \to 0\) で \((e^{\alpha x} - 1)/x \to \alpha\) という命題からも示せる。

§208 極限を使った指数関数の表現

第四章の §73 では \(\{1 + (1/n)\}^{n}\) が \(n \to \infty\) のとき極限に向かうと示し、この極限を仮に \(e\) と表記した。ここまでの議論で定義した \(e\) がこの極限と等しいことを示そう。さらに、次の等式が表すより一般的な結果も得られる: \[ \lim_{n\to\infty} \left(1 + \frac{x}{n}\right)^{n} = \lim_{n\to\infty} \left(1 - \frac{x}{n}\right)^{-n} = e^{x} \qquad \text{(1)} \] この結果は非常に重要なので、二つの証明を示す。

1. 等式 \[ \frac{d}{dt} \log(1 + xt) = \frac{x}{1 + xt} \] から \[ \lim_{h\to 0} \frac{\log(1 + xh)}{h} = x \] が分かる。\(h = 1/\xi\) とすれば、\(h \to \infty\) および \(h \to -\infty\) のとき \[ \lim \xi \log\left(1 + \frac{x}{\xi}\right) = x \] が分かる。指数関数の連続性より \[ \left(1 + \frac{x}{\xi}\right)^{\xi} = e^{\xi\log\{1+(x/\xi)\}} \to e^{x} \] が \(h \to \infty\) および \(h \to -\infty\) で成り立つ。つまり \[ \lim_{\xi\to\infty} \left(1 + \frac{x}{\xi}\right)^{\xi} = \lim_{\xi\to -\infty} \left(1 + \frac{x}{\xi}\right)^{\xi} = e^{x} \qquad \text{(2)} \] である。

   \(\xi \to \infty\) および \(\xi \to -\infty\) で整数の値だけを考えれば、等式 \(\text{(1)}\) が表す結果が得られる。

2. \(n\) を任意の正の整数とする。どれだけ大きくても構わない。\(x \gt 1\) に対して \[ \int_{1}^{x} \frac{dt}{t^{1+(1/n)}} \lt \int_{1}^{x} \frac{dt}{t} \lt \int_{1}^{x} \frac{dt}{t^{1-(1/n)}} \] だから、 \[ n(1 - x^{-1/n}) \lt \log x \lt n(x^{1/n} - 1) \qquad \text{(3)} \] が成り立つ。

   \(y = \log x\) とすれば \(y\) は正で \(x = e^{y}\) であり、簡単な変形から \[ \left(1 + \frac{y}{n}\right)^{n} \lt x \lt \left(1 - \frac{y}{n}\right)^{-n} \qquad \text{(4)} \] が得られる。さらに \[ 1 + \frac{y}{n} = \eta_{1},\quad 1 - \frac{y}{n} = \frac{1}{\eta_{2}} \] とすれば十分大きい \(n\) で \(0 \lt \eta_{1} \lt \eta_{2}\) だから、§74 の \(\text{(9)}\) から \[ \eta_{2}^{n} - \eta_{1}^{n} \lt n\eta_{2}^{n-1} (\eta_{2} - \eta_{1}) = \frac{y^{2}\eta_{2}^{n}}{n} \] が分かり、これは \(n \to \infty\) で \(0\) に向かう。よって \(\text{(4)}\) から示すべき結果が得られる。\(1/n\) を連続変数 \(h\) に置き換えればより一般的な \(\text{(2)}\) も同様に示せる。

§209 極限を使った対数関数の表現

§75 の内容を使って次の等式を示そう: \[ \lim n(1 - x^{-1/n}) = \lim n(x^{1/n} - 1) = \log x \]

\(n \to \infty\) のとき \(n(x^{1/n} - 1)\) は極限に向かい (§75) \(x^{1/n}\) は \(1\) に向かう (例 27.10) ので、 \[ n(x^{1/n} - 1) - n(1 - x^{-1/n}) = n(x^{1/n} - 1)(1 - x^{-1/n}) \] は \(0\) に向かう。よって §208 の不等式 \(\text{(3)}\) から結果が得られる。

§210 一般の対数

対数が数値計算で使われることを読者は知っているだろう。初等代数では \(a\) を底とした \(x\) の対数 \(\log_{a} x\) を次の等式で定義する: \[ x = a^{y},\quad y = \log_{a} x \] 見過ごされることも多いが、この定義は \(y\) が有理数のときしか意味を持たない。

今まで使ってきた対数は底が \(e\) であり、数値計算では底が \(10\) の対数が使われる。ここで \[ y = \log x = \log_{e} x,\quad z = \log_{10} x \] とすれば \(x = e^{y}\) かつ \(x = 10^{z} = e^{z\log 10}\) となる。よって \[ \log_{10} x = \frac{\log_{e} x}{\log_{e} 10} \] であり、\(\log_{e} 10\) さえ計算されていれば底が異なる対数の間で変換が可能になる。

対数の実際的な利用法について細かく議論するのはこの本の目的ではない。この話題について知らない場合には、初等代数や三角法の教科書を参照するとよい⁴。

§211 対数を使った収束判定法

第八章の §175 と §176 では \[ \sum_{1}^{\infty} \frac{1}{n^{s}},\quad \int_{a}^{\infty} \frac{dx}{x^{s}}\qquad (a \gt 0) \] が \(s \gt 1\) なら収束し、\(s \leq 1\) なら発散すると示した。例えば \(\sum (1/n)\) は発散するが、任意の正の実数 \(\alpha\) に対する \(\sum n^{-1-\alpha}\) は収束する。

しかし §200 で見たように、対数関数を使うと \(n \to \infty\) のときに \(0\) に向かう速度が \(1/n\) よりも速く任意に小さい正の \(\alpha\) に対して \(n^{-1-\alpha}\) よりも遅い関数を作れる。例えば \(1/(n\log n)\) はそのような関数であり、そのため \[ \sum \frac{1}{n\log n} \] が収束するのか発散するのかという問題には \(\sum n^{-s}\) という形をした級数との比較では答えを出せない。

あるいは次の級数でも同じことが言える: \[ \sum \frac{1}{n(\log n)^{2}},\quad \sum \frac{\log\log n}{n\sqrt{\log n}} \] こういった級数の収束または発散を判定する問題に興味が生まれる。その判定法は §174 の積分判定法から導ける。

次の等式が成り立つ: \[ D_{x}(\log x)^{1-s} = \frac{1 - s}{x(\log x)^{s}},\quad D_{x}\log\log x = \frac{1}{x\log x} \] ここから \(a \gt 1\) に対して \[ \int_{a}^{\xi} \frac{dx}{x(\log x)^{s}} = \frac{(\log\xi)^{1-s} - (\log a)^{1-s}}{1 - s},\quad \int_{a}^{\xi} \frac{dx}{x\log x} = \log\log \xi - \log\log a \] だと分かる。\(\xi \to \infty\) のとき一つ目の積分は \(s \gt 1\) なら極限 \(-(\log a)^{1-s}/(1 - s)\) に向かい、\(s \lt 1\) なら \(\infty\) に向かう。二つ目の積分は常に \(\infty\) に向かう。よって \(1\) より大きい \(n_{0}\) と \(a\) に対する級数および積分 \[ \sum_{n_{0}}^{\infty} \frac{1}{n(\log n)^{s}},\quad \int_{a}^{\infty} \frac{dx}{x(\log x)^{s}} \] は \(s \gt 1\) なら収束し、\(s \leq 1\) なら発散する。

ここから、ある \(s \gt 1\) があって全ての \(n\) に対して \(\phi(n)\) が \(K/\{n(\log n)^{s}\}\) より小さいなら \(\sum \phi(n)\) が収束すること、およびある有限の値より大きい全ての \(n\) で \(\phi(n)\) が \(K/(n\log n)\) より大きいなら \(\sum \phi(n)\) が発散することが分かる。積分についても同様の結果が得られるが、これは読者に任せる。

§212 指数関数と対数関数に関する級数

指数関数の任意の次数の導関数は指数関数に等しいから、とある \(\theta\) (\(0 \lt \theta \lt 1\)) で \[ e^{x} = 1 + x + \frac{x^{2}}{2!} + \cdots + \frac{x^{n-1}}{(n - 1)!} + \frac{x^{n}}{n!} e^{\theta x} \] が成り立つ。例 27.12 からは \(x\) の値に関わらず \(n \to \infty\) で \(\dfrac{x^{n}}{n!} \to 0\) が分かるので、\(n\) を \(\infty\) に向かわせることで \[ e^{x} = 1 + x + \frac{x^{2}}{2!} + \cdots + \frac{x^{n}}{n!} + \cdots \qquad \text{(1)} \] を得る。

右辺の級数を指数級数 (exponential series) と呼ぶ。特に \[ e = 1 + 1 + \frac{1}{2!} + \cdots + \frac{1}{n!} + \cdots \qquad \text{(2)} \] であり、ここから指数定理 (exponential theorem) として知られる等式 \[ \left(1 + 1 + \frac{1}{2!} + \cdots + \frac{1}{n!} + \cdots\right)^{x} = 1 + x + \frac{x^{2}}{2!} + \cdots + \frac{x^{n}}{n!} + \cdots \qquad \text{(3)} \] を得る。また \[ a^{x} = e^{x\log a} = 1 + (x\log a) + \frac{(x\log a)^{2}}{2!} + \cdots \qquad \text{(4)} \] が全ての正の \(a\) に対して成り立つ。

§213 対数級数

関数のべき級数への展開で重要なものにもう一つ \(\log(1 + x)\) の展開がある。等式 \[ \log(1 + x) = \int_{0}^{x} \frac{dt}{1 + t} \] と \(-1 \lt t \lt 1\) で成り立つ展開 \(1/(1 + t) = 1 - t + t^{2} - \cdots\) から、級数 \(1 - t + t^{2} - \cdots\) を項ごとに \(t = 0\) から \(t = x\) まで積分した級数 \(x - \frac{1}{2} x^{2} + \frac{1}{3} x^{3} - \cdots\) が \(\log(1 + x)\) の展開になっていると予想できる。これが実際に正しいことを示そう。 \[ \frac{1}{1 + t} = 1 - t + t^{2} - \cdots + (-1)^{m-1} t^{m-1} + \frac{(-1)^{m} t^{m}}{1 + t} \] が成り立つから、\(x \gt -1\) で \[ \log(1 + x) = \int_{0}^{x} \frac{dt}{1 + t} = x - \frac{x^{2}}{2} + \cdots + (-1)^{m-1} \frac{x^{m}}{m} + (-1)^{m} R_{m} \] が分かる。ここで \(R_{m}\) は次の通りである: \[ R_{m} = \int_{0}^{x} \frac{t^{m}\, dt}{1 + t} \]

\(m\) が \(\infty\) に向かうときの \(R_{m}\) の極限が \(0\) だと示す必要があるが、これは \(0 \lt x \leq 1\) ならほぼ自明に分かる: このとき \(R_{m}\) は正で \[ \int_{0}^{x} t^{m}\, dt = \frac{x^{m+1}}{m + 1} \] より小さい。つまり \(1/(m + 1)\) より小さい。一方で \(-1 \lt x \lt 0\) なら \(t = -u\) および \(x = -\xi\) と置換すれば \[ R_{m} = (-1)^{m} \int_{0}^{\xi} \frac{u^{m}\, du}{1 - u} \] が成り立つ。よって \(R_{m}\) は \((-1)^{m}\) と同じ符号を持つ。さらに積分区間内の \(1/(1 - u)\) の最大値は \(1/(1 - \xi)\) だから \[ 0 \lt |R_{m}| \lt \frac{1}{1 - \xi} \int_{0}^{\xi} u^{m}\, du = \frac{\xi^{m}}{(m + 1)(1 - \xi)} \lt \frac{1}{(m + 1)(1 - \xi)} \] であり、ここから \(R_{n} \to 0\) が分かる。

したがって \[ \log(1 + x) = x - \dfrac{1}{2} x^{2} + \dfrac{1}{3} x^{3} - \cdots \] が \(-1 \lt x \leq 1\) で成り立つ。\(x\) がこの区間外にあるなら級数は収束しない。また \(x = 1\) とした \[ \log 2 = 1 - \dfrac{1}{2} + \dfrac{1}{3} - \cdots \] は前に別の方法で示した (例 89.7)。

§214 \(\arctan x\) の級数展開

同様に \(-1 \leq x \leq 1\) で \[ \begin{aligned} \arctan x = \int_{0}^{x} \frac{dt}{1 + t^{2}} & = \int_{0}^{x}(1 - t^{2} + t^{4} - \cdots)\, dt\\ & = x - \dfrac{1}{3} x^{3} + \dfrac{1}{5} x^{5} - \cdots \end{aligned} \] だと容易に示せる。\(\log (1 + x)\) の展開と比べると、この等式の証明の方が簡単になる点が唯一異なる。というのも \(\arctan x\) は \(x\) の奇関数なので、正の \(x\) だけを考えればよい。またこの級数は \(x = 1\) だけでなく \(x = -1\) でも収束する。この級数で表される \(\arctan x\) の値は \(-1 \leq x \leq 1\) に対応する \(-\frac{1}{4}\pi\) と \(\frac{1}{4}\pi\) の間となる。この積分の値は第七章の 例 63.3 で求めた。また \(x = 1\) とすれば次の等式を得る: \[ \dfrac{1}{4}\pi = 1 - \dfrac{1}{3} + \dfrac{1}{5} - \cdots \]

§215 二項級数

§163 では、二項定理 \[ (1 + x)^{m} = 1 + \binom{m}{1}x + \binom{m}{2}x^{2} + \cdots \] が \(-1 \lt x \lt 1\) と有理数 \(m\) に対して成り立つことを見た。\(m\) が無理数なら \[ \begin{gathered} (1 + x)^{m} = e^{m\log(1+ x)},\\ D_{x}(1 + x)^{m} = \{m/(1 + x)\} e^{m\log(1 + x)} = m(1 + x)^{m-1} \end{gathered} \] が成り立つので、\((1 + x)^{m}\) の導関数を表す等式は変わらない。よって §163 で示した二項定理の証明をここでも適用できる。本書では \(x = 1\) と \(x = -1\) における収束性は議論しない¹⁰。

§216 対数および指数の理論の異なる構築方法

\(e^{x}\) と \(\log x\) の性質をこれまでとは全く異なる論理展開で調べる方法の概略をここに示す。この方法は指数級数 \(1 + x + \dfrac{x^{2}}{2!} + \cdots\) の考察から始まる。この級数が全ての \(x\) で収束することは分かっているので、関数 \(\exp x\) を次の等式で定義する: \[ \exp x = 1 + x + \frac{x^{2}}{2!} + \cdots \qquad \text{(1)} \]

そして 例 81.7 と同様に \[ \exp x × \exp y = \exp(x + y) \qquad \text{(2)} \] を証明する。

さらに \[ \frac{\exp h - 1}{h} = 1 + \frac{h}{2!} + \frac{h^{2}}{3!} + \cdots = 1 + \rho(h) \] とすれば、\(\rho(h)\) の絶対値は \[ \left|\dfrac{1}{2}h\right| + \left|\dfrac{1}{2}h\right|^{2} + \left|\dfrac{1}{2}h\right|^{3} + \cdots = \left|\dfrac{1}{2}h \right| \bigg/ \left(1 - |\dfrac{1}{2}h| \right) \] よりも小さい。ここから \(h \to 0\) のとき \(\rho(h) \to 0\) と分かる。よって \(h \to 0\) で \[ \frac{\exp(x + h) - \exp x}{h} = \exp x \left(\frac{\exp h - 1}{h}\right) \to \exp x \] つまり \[ D_{x} \exp x = \exp x \qquad \text{(3)} \] が成り立つ。ここでは \(\exp x\) が連続関数であることも同時に証明されている。

ここからはいくつか方法がある。\(\exp 0 = 1\) だから、\(y = \exp x\) と書けば \[ \frac{dy}{dx} = y,\quad x = \int_{1}^{y} \frac{dt}{t} \] となる。よって対数関数を指数関数の逆関数として定義すれば、この章の最初のスタート地点に戻れる。

異なる議論もできる。\(\text{(2)}\) から正の整数 \(n\) に対して \[ (\exp x)^{n} = \exp nx,\quad (\exp 1)^{n} = \exp n \] が分かる。よって \(x\) が正の有理数 \(m/n\) なら \[ \{\exp(m/n)\}^{n} = \exp m = (\exp 1)^{m} \] が成り立つ。つまり \(\exp(m/n)\) は \(\exp 1^{m/n}\) の正の値となる。この結果は次の等式を使えば負の有理数にも拡張できる: \[ \exp x \exp(-x) = 1 \] ここから \[ \exp x = (\exp 1)^{x} = e^{x} \] が導かれる。ここで \[ e = \exp 1 = 1 + 1 + \frac{1}{2!} + \frac{1}{3!} + \cdots \] であり、\(x\) は任意の有理数を表す。\(x\) が無理数のときには \(e^{x}\) を \(\exp x\) として定義し、対数は \(\exp x\) つまりは \(e^{x}\) の逆関数として定義する。

第九章に関するその他の例

1. \(2^{10}\) と \(3^{21}\) の桁数がほぼ等しい事実と \(\log_{10} e = .4343\) という近似を使って、\(\log_{10} 2\) と \(\log_{10} 3\) の値を小数点以下第四位まで計算せよ。

   (Math. Trip. 1905.)

2. \((\frac{1}{2}e)^{\sqrt{3}}\) と \((\sqrt{2})^{\frac{1}{2}\pi}\) のどちらが大きいか答えよ。 [対数を取って \(\sqrt{3}/(\sqrt{3} + \frac{1}{4}\pi) \lt \frac{2}{5} \sqrt{3} \lt .6929 \lt \log 2\) を使う]

3. \(\log_{10} n\) は \(n\) が \(10\) のべきでない限り整数とならない。 [\(10\) の倍数でない \(n\) に対して \(\log_{10}n = p/q\) が成り立つなら \(10^{p} = n^{q}\) となるが、\(10^{p}\) は \(0\) で終わるのに対して \(n^{q}\) はそうでないので、これはあり得ない。また \(10\) の倍数でない \(N\) を使って \(n = 10^{a}N\) と書けるなら \[ \log_{10}n = a + \log_{10}N \] は有理数でない]

4. 関数 \(\log x,\ \log\log x,\ \log\log\log x,\ \ldots\) が (a) \(0\) になる (b) \(1\) になる (c) 定義されない \(x\) の値は何か？ \(lx = \log |x|\) に対する \(lx,\ llx,\ lllx,\ \ldots\) についても同様のことを考えよ。

5. \(x\) が \(0\) から \(\infty\) に増加するとき \[ \log x - \binom{n}{1} \log(x + 1) + \binom{n}{2} \log(x + 2) - \cdots + (-1)^{n} \log(x + n) \] が常に負で、\(0\) に向かって単調に増加することを示せ。

   [この関数の導関数は \[ \sum_{0}^{n} (-1)^{r} \binom{n}{r} \frac{1}{x + r} = \frac{n!}{x(x + 1) \cdots (x + n)} \] である。この等式は右辺を部分分数分解すれば容易に分かる。ここから導関数が常に正と分かる。またこの関数が \(x \to \infty\) で \(0\) に向かうことは、 \[ \log(x + r) = \log x + \varepsilon_{x} \] とすれば \(\varepsilon_{x} \to 0\) となること、および \(1 - \dbinom{n}{1} + \dbinom{n}{2} - \cdots = 0\) から分かる]

6. 次を示せ: \[ \left(\frac{d}{dx}\right)^{n} \frac{\log x}{x} = \frac{(-1)^{n} n!}{x^{n+1}} \left(\log x - 1 - \frac{1}{2} - \cdots - \frac{1}{n}\right) \]

   (Math. Trip. 1909.)

7. \(x \gt -1\) で \(x^{2} \gt (1 + x) \{\log(1 + x)\}^{2}\) が成り立つ。

   (Math. Trip. 1906.)

   [\(1 + x = e^{\xi}\) として、\(\xi \gt 0\) で \(\sinh \xi \gt \xi\) となる事実を使う]

8. \(x\) が \(0\) から \(\infty\) まで増加するとき \(\dfrac{\log(1 + x)}{x}\) と \(\dfrac{x}{(1 + x)\log(1 + x)}\) の両方が単調に減少することを示せ。

9. \(x\) が \(-1\) から \(\infty\) に増加するとき、関数 \((1 + x)^{-1/x}\) が \(0\) から \(1\) の値を一度ずつ取ることを示せ。

   (Math. Trip. 1910.)

10. \(x \to 0\) のとき \(\dfrac{1}{\log(1 + x)} - \dfrac{1}{x} \to \dfrac{1}{2}\) だと示せ。

11. \(x\) が \(-1\) から \(\infty\) に増加するとき \(\dfrac{1}{\log(1 + x)} - \dfrac{1}{x}\) が \(1\) から \(0\) へ単調に減少することを示せ。 [この関数は \(x = 0\) で定義されないが、\(x = 0\) で \(\dfrac{1}{2}\) と定めれば \(x = 0\) で連続となる。導関数が負であることを示すには問題 7 を使う]

12. \(\xi\) を正とする。\(x\) が \(0\) から \(\xi\) まで増加するとき \(\dfrac{\log \xi - \log x}{\xi - x}\) が単調に減少することを示せ。\(x \to \xi\) における極限を求めよ。

13. \(M\) と \(N\) を大きな正の実数とする。\(x\) が \(2\log M\) と \(16N^{2}\) の両方より大きいなら \(e^{x} \gt Mx^{N}\) だと示せ。

    [\(\log x \lt 2\sqrt{x}\) は容易に示せる。よって与えられた不等式は \[ x \gt \log M + 2N\sqrt{x} \] なら満たされる。つまり \(\dfrac{1}{2}x \gt \log M\) かつ \(\dfrac{1}{2}x \gt 2N\sqrt{x}\) であればよい]

14. \(x \to \infty\) のとき \(f(x)\) と \(\phi(x)\) が無限大に向かうとする。\(f'(x)/\phi'(x) \to \infty\) なら \(f(x)/\phi(x) \to \infty\) だと示せ。 [第六章に関するその他の例 33 の結果を使う。\(f(x) = x^{\alpha}\) および \(\phi(x) = \log x\) とすれば、任意の正の \(\alpha\) に対して \((\log x)/x^{\alpha} \to 0\) が示せる]

15. \(p\) と \(q\) を正の整数とする。このとき \(n \to \infty\) で \[ \frac{1}{pn + 1} + \frac{1}{pn + 2} + \cdots + \frac{1}{qn} \to \log\left(\frac{q}{p}\right) \] が成り立つ。 [参考: 例 78.6]

16. \(x\) が正なら \(n \to \infty\) で \(n\log\{\dfrac{1}{2}(1 + x^{1/n})\} \to -\dfrac{1}{2}\log x\) だと示せ。 [\(u = \frac{1}{2}(1 - x^{1/n})\) とすれば \[ n\log\{\dfrac{1}{2}(1 + x^{1/n})\} = n\log\{1 - \dfrac{1}{2}(1 - x^{1/n})\} = \dfrac{1}{2}n(1 - x^{1/n}) \frac{\log(1 - u)}{u} \] が成り立つ。§209 と 例 82.4 を使う]

17. \(a\) と \(b\) が正なら \[ \left\{\dfrac{1}{2}(a^{1/n} + b^{1/n})\right\}^{n} \to \sqrt{ab} \] だと示せ。 [対数を取って問題 16 を使う]

18. 次を示せ: \[ 1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{2n - 1} = \dfrac{1}{2}\log n + \log 2 + \dfrac{1}{2} \gamma + \varepsilon_{n} \] ここで \(\gamma\) はオイラーの定数 (例 89.1) で、\(n \to \infty\) のとき \(\varepsilon_{n} \to 0\) とする。

19. 次を示せ: \[ 1 + \dfrac{1}{3} - \dfrac{1}{2} + \dfrac{1}{5} + \dfrac{1}{7} - \dfrac{1}{4} + \dfrac{1}{9} + \cdots = \dfrac{3}{2} \log 2 \] これは級数 \(1 - \dfrac{1}{2} + \dfrac{1}{3} - \cdots\) から二つの正の項と一つの負の項を順に取ることで得られる。 [最初の \(3n\) 項の和は \[ \begin{aligned} & 1 + \frac{1}{3} + \frac{1}{5} + \cdots + \frac{1}{4n - 1} - \frac{1}{2} \left(1 + \frac{1}{2} + \cdots + \frac{1}{n}\right)\\ & \qquad \qquad = \dfrac{1}{2}\log 2n + \log 2 + \dfrac{1}{2}\gamma + \varepsilon_{n} - \dfrac{1}{2}(\log n + \gamma + \varepsilon_{n}') \end{aligned} \] となる (参考: 例 78.6)。ここで \(\varepsilon_{n}\) と \(\varepsilon'_{n}\) は \(n \to \infty\) のとき \(0\) に向かう]

20. \(1 - \dfrac{1}{2} - \dfrac{1}{4} + \dfrac{1}{3} - \dfrac{1}{6} - \dfrac{1}{8} + \dfrac{1}{5} - \dfrac{1}{10} - \cdots = \dfrac{1}{2}\log 2\) を示せ。

21. 次を示せ: \[ \sum_{1}^{n} \frac{1}{\nu(36\nu^{2} - 1)} = -3 + 3\Sigma_{3n+1} - \Sigma_{n} - S_{n} \] ここで \(S_{n} = 1 + \dfrac{1}{2} + \cdots + \dfrac{1}{n},\ \Sigma_{n} = 1 + \dfrac{1}{3} + \cdots + \dfrac{1}{2n - 1}\) とする。これを使って、 級数を無限に伸ばしたときの和が次に等しいと示せ: \[ -3 + \dfrac{3}{2}\log 3 + 2\log 2 \]

    (Math. Trip. 1905.)

22. 次を示せ: \[ \sum_{1}^{\infty} \frac{1}{n(4n^{2} - 1)} = 2\log 2 - 1, \quad \sum_{1}^{\infty} \frac{1}{n(9n^{2} - 1)} = \dfrac{3}{2}(\log 3 - 1) \]

23. 次の四つの級数を考える: \[ \sum_{1}^{\infty} \frac{1}{4n^{2} - 1},\quad \sum_{1}^{\infty} \frac{(-1)^{n-1}}{4n^{2} - 1},\quad \sum_{1}^{\infty} \frac{1}{(2n + 1)^{2} - 1},\quad \sum_{1}^{\infty} \frac{(-1)^{n-1}}{(2n + 1)^{2} - 1} \] これらの和がそれぞれ \(\dfrac{1}{2},\ \dfrac{1}{4}\pi - \dfrac{1}{2},\ \dfrac{1}{4},\ \dfrac{1}{2}\log 2 - \dfrac{1}{4}\) だと示せ。

24. \(n!\, (a/n)^{n}\) が \(a \lt e\) なら \(0\) に向かい、\(a \gt e\) なら \(\infty\) に向かうと示せ。

    [\(u_{n} = n!\, (a/n)^{n}\) とすれば \(u_{n+1}/u_{n} = a\{1 + (1/n)\}^{-n} \to a/e\) が成り立つ。\(a = e\) ならこの関数は \(\infty\) に向かうと示せるが、その証明はこの章で示した定理の範囲を超える。ブロムウィッチ著 Infinite Series, pp. 261, et seq. を参照]

25. \(x \to \infty\) における \[ \left(\frac{a_{0} + a_{1} x + \cdots + a_{r} x^{r}} {b_{0} + b_{1} x + \cdots + b_{r} x^{r}}\right)^{\lambda_{0}+\lambda_{1}x} \] の極限を求めよ。生じうる場合を全て分けて考えること。

    (Math. Trip. 1886.)

26. 次の級数が発散すると示せ: \[ \sum \log \left(1 + \frac{x}{n}\right)\quad (x \gt 0) \] [\(\sum (x/n)\) と比較する] これを使って、\(x\) が正なら \(n \to \infty\) で \[ \frac{(1 + x)(2 + x) \cdots (n + x)}{n!} \to \infty \] だと示せ。 [この関数の対数は \(\sum\limits_{1}^{n} \log \left(1 + \dfrac{x}{\nu}\right)\) である]

27. \(x \gt -1\) なら \[ \begin{aligned} \frac{1}{(x + 1)^{2}} & = \frac{1}{(x + 1) (x + 2)} + \frac{1!}{(x + 1) (x + 2) (x + 3)}\\ & \qquad + \frac{2!}{(x + 1) (x + 2) (x + 3) (x + 4)} + \cdots \end{aligned} \] だと示せ。

    (Math. Trip. 1908.)

    [級数の最初の \(n\) 項の和と \(1/(x + 1)^{2}\) の差は \[ \frac{1}{(x + 1)^{2}}\, \frac{n!}{(x + 2) (x + 3) \cdots (x + n + 1)} \] と表せる]

28. 次の等式が全ての \(x\) に対して成り立つことはないと示せ: \[ Ae^{\alpha x} + Be^{\beta x} + \cdots = 0 \] \(A,\ B,\ \ldots\) は多項式、\(\alpha,\ \beta,\ \ldots\) は異なる実数とする。 [\(\alpha\) を \(\alpha,\ \beta,\ \ldots\) の最大値とすると、\(x \to \infty\) において \(Ae^{\alpha x}\) が他の項より圧倒的に大きくなる]

29. 数列 \[ a_{1} = e,\quad a_{2} = e^{e^{2}},\quad a_{3} = e^{e^{e^{3}}},\ \ldots \] が任意の指数尺度よりも速く無限大に向かうと示せ。

    [\(e_{1}(x) = e^{x},\ e_{2}(x) = e^{e_{1}(x)},\ \ldots\) とすると、任意の指数尺度 \(e_{k}(x)\) に対して \(n \gt k\) で \(a_{n} \gt e_{k}(n)\) が成り立つ]

30. 次を示せ: \[ \frac{d}{dx} \{\phi(x)\}^{\psi(x)} = \frac{d}{dx} \{\phi(x)\}^{\alpha} + \frac{d}{dx} \{\beta^{\psi(x)}\} \] 右辺では微分を計算してから \(\alpha\) に \(\psi(x)\) を、\(\beta\) に \(\phi(x)\) を代入する。\(\phi(x)^{[\{\psi(x)\}^{\chi(x)}]}\) に対する同様の微分公式を示せ。

31. \(D_{x}^{n} e^{-x^{2}} = e^{-x^{2}} \phi_{n}(x)\) とする。このとき (i) \(\phi_{n}(x)\) が次数 \(n\) の多項式であること (ii) \(\phi_{n+1} = -2x\phi_{n} + \phi_{n}'\) が成り立つこと (iii) \(\phi_{n} = 0\) の根が相異なる実数であり、\(\phi_{n-1} = 0\) の根で分離されることをそれぞれ示せ。 [(iii) の証明では \(\kappa = 1,\ 2,\ \ldots,\ n\) に対する成立を仮定し、\(\phi_{n} = 0\) が成立する \(n\) 個の \(x\) および十分大きな正と負の \(x\) における \(\phi_{n+1}\) の符号を考える]

32. 微分可能な関数 \(f\) に対する関数方程式 \(f(xy) = f(x)f(y)\) の解が \(x^{a}\) だと示せ。\(a\) は定数とする。さらに \[ f(x + y) + f(x - y) = 2f(x)f(y) \] の根が、\(f''(0)\) の正負に応じて \(\cosh ax\) または \(\cos ax\) だと示せ。 [二つ目の結果の証明では \(f\) が三次までの導関数を持つと仮定する。このとき \[ 2f(x) + y^{2}\{f''(x) + \varepsilon_{y}\} = 2f(x)[f(0) + yf'(0) + \dfrac{1}{2} y^{2}\{f''(0) + \varepsilon_{y}'\}] \] であり、\(\varepsilon_{y}\) と \(\varepsilon_{y}'\) は \(y\) と共に \(0\) に向かう。ここから \(f(0) = 1,\ f'(0) = 0f''(x) = f''(0)f(x)\) が導かれ、\(a = \sqrt{f''(0)}\) または \(a = \sqrt{-f''(0)}\) と分かる]

33. 関数 \(x^{\sin(1/x)},\ x^{\sin^{2}(1/x)},\ x^{\cosec(1/x)}\) は \(x \to +0\) でどう振る舞うか？

34. 曲線 \(y = \tan x e^{\tan x},\ y = \sin x \log \tan \dfrac{1}{2}x\) を描け。

35. 方程式 \(e^{x} = ax + b\) は \(a \lt 0\) または「\(a = 0,\ b \gt 0\)」のとき一つの実根を持つ。\(a \gt 0\) の場合は \(a\log a \gt b - a\) か \(a\log a \lt b - a\) かに応じて二つまたは零個の実根を持つ。

36. 幾何学的な考察によって、方程式 \(e^{x} = ax^{2} + 2bx + c\) の実根の数が \(a \gt 0\) なら \(1,\ 2,\ 3\) のどれかであり、\(a \lt 0\) なら \(0,\ 1,\ 2\) のどれかだと示せ。それぞれの場合を区別する方法を説明せよ。

37. 曲線 \(y = \dfrac{1}{x} \log\left(\dfrac{e^{x} - 1}{x}\right)\) を描け。この曲線が点 \((0, \frac{1}{2})\) に関して対称であり、\(x\) が全ての実数の値を取りながら増加するとき \(y\) は \(0\) から \(1\) へ単調に増加することを示せ。グラフから方程式 \[ \frac{1}{x} \log\left(\frac{e^{x} - 1}{x}\right) = \alpha \] には \(0 \lt \alpha \lt 1\) でない限り実根が存在しないこと、そして実根が存在するなら符号が \(\alpha - \frac{1}{2}\) と等しいことを導け。 [まず \[ y - \dfrac{1}{2} = \frac{1}{x} \left\{\log\left(\frac{e^{x} - 1}{x}\right) - \log e^{\frac{1}{2} x}\right\} = \frac{1}{x} \log\left(\frac{\sinh \frac{1}{2}x}{\frac{1}{2}x}\right) \] は明らかに \(x\) の奇関数である。また \[ \frac{dy}{dx} = \frac{1}{x^{2}} \left\{\dfrac{1}{2} x\coth \dfrac{1}{2}x - 1 - \log\left(\frac{\sinh \frac{1}{2}x}{\frac{1}{2}x}\right)\right\} \] であり、中括弧の中の関数は \(x \to 0\) で \(0\) に向かう。さらにこの導関数 \[ \frac{1}{x} \left\{1 - \left(\frac{\frac{1}{2}x}{\sinh \frac{1}{2}x}\right)^2\right\} \] は \(x\) と同じ符号を持つので、全ての \(x\) で \(dy/dx \gt 0\) が成り立つ]

38. 曲線 \(y = e^{1/x} \sqrt{x^{2} + 2x}\) を描き、方程式 \[ e^{1/x} \sqrt{x^{2} + 2x} = \alpha \] が \(\alpha\) が負のとき実根を持たないことを示せ。さらに \[ 0 \lt \alpha \lt a = e^{1/\sqrt{2}} \sqrt{2 + 2\sqrt{2}} \] なら一つの負の根を、\(\alpha \gt a\) なら二つの正の根と一つの負の根を持つと示せ。

39. 方程式 \(f_{n}(x) = 1 + x + \dfrac{x^{2}}{2!} + \cdots + \dfrac{x^{n}}{n!} = 0\) は \(n\) が奇数なら実根を一つ持ち、\(n\) が偶数なら実根を持たないことを示せ。

    [この命題が \(n = 1,\ 2,\ \ldots 2k\) で成り立つと仮定する。\(f_{2k+1}(x) = 0\) の次数は奇数だから、少なくとも一つの実根を持つ。仮に実根が一つより多いなら \(f'_{2k+1}(x)\) つまり \(f_{2k}(x)\) が少なくとも一度 \(0\) にならなければならないので、実根は一つしか存在しない。よって \(f_{2k+1}(x) = 0\) の実根は一つだけであり、\(f_{2k+2}(x) = 0\) の実根は二つ以下である。もし実根が \(\alpha\) と \(\beta\) の二つだとすると、\(f'_{2k+2}(x)\) つまり \(f_{2k+1}(x)\) が \(\alpha\) と \(\beta\) の間で少なくとも一回 \(0\) になる。この点を \(\gamma\) とすると \[ f_{2k+2}(\gamma) = f_{2k+1}(\gamma) + \frac{\gamma^{2k+2}}{(2k + 2)!} \gt 0 \] が成り立つ。一方で \(f_{2k+2}(x)\) は正および負の大きい \(x\) で正だから、グラフを一瞥すればこの結果が矛盾すると分かる。よって \(f_{2k+2}(x) = 0\) は実根を持たない]

40. \(a\) と \(b\) が正でほぼ等しいなら近似的に \[ \log \frac{a}{b} = \frac{1}{2}(a - b) \left(\frac{1}{a} + \frac{1}{b}\right) \] であり、誤差が \(\frac{1}{6}\{(a - b)/a\}^{3}\) にほぼ等しいと示せ。 [対数級数を使う。これはネイピアが対数の数値計算に利用した歴史的に重要な公式である]

41. 級数の積を使って、\(-1 \lt x \lt 1\) で \[ \begin{aligned} \dfrac{1}{2}\{\log(1 + x)\}^{2} & = \dfrac{1}{2} x^{2} - \dfrac{1}{3}(1 + \dfrac{1}{2})x^{3} + \dfrac{1}{4}(1 + \dfrac{1}{2} + \dfrac{1}{3})x^{4} - \cdots,\\ \dfrac{1}{2}(\arctan x)^{2} & = \dfrac{1}{2} x^{2} - \dfrac{1}{4}(1 + \dfrac{1}{3})x^{4} + \dfrac{1}{6}(1 + \dfrac{1}{3} + \dfrac{1}{5})x^{6} - \cdots \end{aligned} \] が成り立つと示せ。

42. 次を示せ: \[ (1 + a x)^{1/x} = e^{a}\{1 - \dfrac{1}{2} a^{2}x + \dfrac{1}{24}(8 + 3a)a^{3}x^{2}(1 + \varepsilon_{x})\} \] \(\varepsilon_{x}\) は \(x\) と共に \(0\) へ向かうとする。

43. \(\log\left(1 + x + \dfrac{x^{2}}{2!} + \cdots + \dfrac{x^{n}}{n!}\right)\) を \(x\) のべき級数に展開したときの最初の \(n + 2\) 項は \[ x - \frac{x^{n+1}}{n!} \left\{\frac{1}{n + 1} - \frac{x}{1!\, (n + 2)} + \frac{x^{2}}{2!\, (n + 3)} - \cdots + (-1)^{n} \frac{x^{n}}{n!\, (2n + 1)} \right\} \] である。

    (Math. Trip. 1899.)

44. 関数 \[ \exp \left(-x - \frac{x^{2}}{2} - \cdots - \frac{x^{n}}{n}\right) \] の \(x\) のべき級数への展開が \[ 1 - x + \frac{x^{n+1}}{n + 1} - \sum_{s=1}^{n} \frac{x^{n+s+1}}{(n + s)(n + s + 1)} \] で始まると示せ。

    (Math. Trip. 1909.)

45. \(-1 \lt x \lt 1\) で次が成り立つと示せ: \[ \begin{aligned} \frac{1}{3}x + \frac{1·4}{3·6}2^{2}x^{2} + \frac{1·4·7}{3·6·9}3^{2}x^{3} + \cdots & = \frac{x(x + 3)}{9(1 - x)^{7/3}},\\ \frac{1}{3}x + \frac{1·4}{3·6}2^{3}x^{2} + \frac{1·4·7}{3·6·9}3^{3}x^{3} + \cdots & = \frac{x(x^{2} + 18x + 9)}{27(1 - x)^{10/3}} \end{aligned} \] [例 92.6 の方法を使う。微分を使えばより簡単にこの結果を得られるが、無限級数の微分に関する話題は本書の範囲を超える]

46. 次を示せ: \[ \begin{aligned} \int_{0}^{\infty} \frac{dx}{(x + a)(x + b)} & = \frac{1}{a - b} \log\left(\frac{a}{b}\right), \\ \int_{0}^{\infty} \frac{dx}{(x + a)(x + b)^{2}} & = \frac{1}{(a - b)^{2}b}\left\{a - b - b\log\left(\frac{a}{b}\right)\right\},\\ \int_{0}^{\infty} \frac{x\, dx}{(x + a)(x + b)^{2}} & = \frac{1}{(a - b)^{2}} \left\{a\log\left(\frac{a}{b}\right) - a + b\right\},\\ \int_{0}^{\infty} \frac{dx}{(x + a)(x^{2} + b^{2})} & = \frac{1}{(a^{2} + b^{2})b} \left\{\dfrac{1}{2}\pi a - b\log\left(\frac{a}{b}\right)\right\},\\ \int_{0}^{\infty} \frac{x\, dx}{(x + a)(x^{2} + b^{2})} & = \frac{1}{a^{2} + b^{2}} \left\{\dfrac{1}{2}\pi b + a\log\left(\frac{a}{b}\right)\right\} \end{aligned} \] \(a\) と \(b\) は正とする。この結果を使って、次の関数が全ての正の \(a\) に対して常に正だと示せ: \[ a - 1 - \log a,\quad a\log a - a + 1,\quad \dfrac{1}{2}\pi a - \log a,\quad \dfrac{1}{2}\pi + a\log a \] さらに同じことを独立に確認せよ。

47. \(\alpha,\ \beta,\ \gamma\) が全て正で \(\beta^{2} \gt \alpha\gamma\) なら \[ \int_{0}^{\infty} \frac{dx}{\alpha x^{2} + 2\beta x + \gamma} = \frac{1}{\sqrt{\beta^{2} - \alpha\gamma}} \log \left\{\frac{\beta + \sqrt{\beta^{2} - \alpha\gamma}} {\sqrt{\alpha\gamma}} \right\} \] であり、\(\alpha\) が正で \(\alpha\gamma \gt \beta^{2}\) なら積分の値は \[ \frac{1}{\sqrt{\alpha\gamma - \beta^{2}}} \arctan \left\{\frac{\sqrt{\alpha\gamma - \beta^{2}}}{\beta}\right\} \] だと示せ。タンジェントの逆関数は \(0\) から \(\pi\) の値を取るとする。この二つと本質的に異なる場合に積分が収束することはあるか？

48. \(a \gt -1\) とする。 \[ \int_{1}^{\infty} \frac{dx}{(x + a)\sqrt{x^{2} - 1}} = \int_{0}^{\infty} \frac{dt}{\cosh t + a} = 2\int_{1}^{\infty}\frac{du}{u^{2} + 2au + 1} \] を示し、この積分の値が \(-1 \lt a \lt 1\) なら \[ \frac{2}{\sqrt{1 - a^{2}}} \arctan \sqrt{\frac{1 - a}{1 + a}} \] であり、\(a \gt 1\) なら \[ \frac{1}{\sqrt{a^{2} - 1}} \log\frac{\sqrt{a + 1} + \sqrt{a - 1}} {\sqrt{a + 1} - \sqrt{a - 1}} = \frac{2}{\sqrt{a^{2} - 1}} \text{argtanh} \sqrt{\frac{a - 1}{a + 1}} \] だと示せ。\(a = 1\) の場合を議論せよ。

49. 同様の方法で \(a \gt 0\) に対する積分 \(\displaystyle\int_{0}^{\infty} \frac{dx}{(x + a) \sqrt{x^{2} + 1}}\) を変形し、この値が \[ \frac{1}{\sqrt{a^{2} + 1}} \log\frac{a + 1 + \sqrt{a^{2} + 1}}{a + 1 - \sqrt{a^{2} + 1}} = \frac{2}{\sqrt{a^{2} + 1}} \text{argtanh} \frac{\sqrt{a^{2} + 1}}{a + 1} \] に等しいと示せ。

50. 次を示せ: \[ \int_{0}^{1} \arctan x\, dx = \dfrac{1}{4}\pi - \dfrac{1}{2}\log 2 \]

51. \(0 \lt \alpha \lt 1,\ 0 \lt \beta \lt 1\) で次が成り立つと示せ: \[ \int_{-1}^{1} \frac{dx}{\sqrt{(1 - 2\alpha x + \alpha^{2})(1 - 2\beta x + \beta^{2})}} = \frac{1}{\sqrt{\alpha\beta}} \log \frac{1 + \sqrt{\alpha\beta}}{1 - \sqrt{\alpha\beta}} \]

52. \(a \gt b \gt 0\) なら \[ \int_{-\infty}^{\infty} \frac{d\theta}{a\cosh \theta + b\sinh \theta} = \frac{\pi}{\sqrt{a^{2} - b^{2}}} \] だと示せ。

53. 次を示せ: \[ \int_{0}^{1} \frac{\log x}{1 + x^{2}}\, dx = -\int_{1}^{\infty} \frac{\log x}{1 + x^{2}}\, dx,\quad \int_{0}^{\infty} \frac{\log x}{1 + x^{2}}\, dx = 0 \] ここから \(a \gt 0\) なら \[ \int_{0}^{\infty} \frac{\log x}{a^{2} + x^{2}}\, dx = \frac{\pi}{2a}\log a \] だと導け。

    [置換 \(x = 1/t\) および \(x = au\) を使う]

54. \(a \gt 0\) として次を示せ: \[ \int_{0}^{\infty} \log \left(1 + \frac{a^{2}}{x^{2}}\right) dx = \pi a \] [部分積分を使う]

1. 証明は §133 で示した文献を参照。^[return]

2. "無限大の尺度" に関するさらなる情報は拙著 "Orders of Infinity", Camb. Math. Tracts, No. 12 を参照。^[return]

3. 指数関数は等式 \(y = \log x\) を逆にして \(x = e^{y}\) と書くことで導入されたので、これまでその性質の議論では \(y\) を独立変数として、\(x\) を従属変数としてきた。 しかしここからは \(x\) を独立変数とする通常の表記に戻ることにする。ただし \(y = \log x\) と \(x = e^{y}\) の等式の組を同時に考えるときや何らかの特別な理由がある場合は除く。^[return]

4. 例えばクリスタル著 Algebra, vol. i, ch xxi. など。\(\log_{e} 10\) の値は \(2.302\ldots\) であり、これは \(.434\ldots\) の逆数である。^[return]

5. 訳注: 原文の誤りを修正。^[return]

6. \(\cosh\) はハイパボリックコサイン (hyperbolic cosine) を略している。この言い回しの意味についてはホブソン著 Trigonometry, ch. xvi. を参照。^[return]

7. 言うまでもないが、この "非常に大きい" は第四章で説明した特殊な意味では使われていない。ここでの意味は「初等数学で普通に目にする方程式の根よりずっと大きい」である。"少しだけ大きい" についても同様。^[return]

8. §202 の脚注を参照。^[return]

9. \(D_{x}^{n} \arctan x\) の式には \(\arctan(1/x)\) が含まれるので、\(x = 0\) で定義されない。しかしこの場合の \(\arctan(1/x)\) が \(\frac{1}{2}\pi\) を意味していることは容易に分かる (参考: 例 45.11)。^[return]

10. Bromwich, Infinite Series, pp. 150 et seq. および Hobson, Plane Trigonometry (3rd edition), p. 271. を参照。^[return]