§25 有理関数 (その 2)

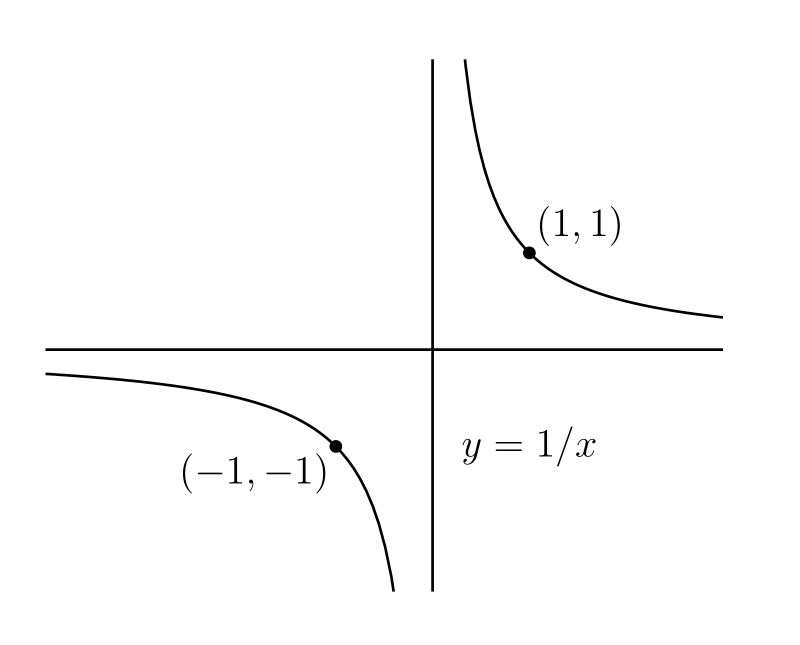
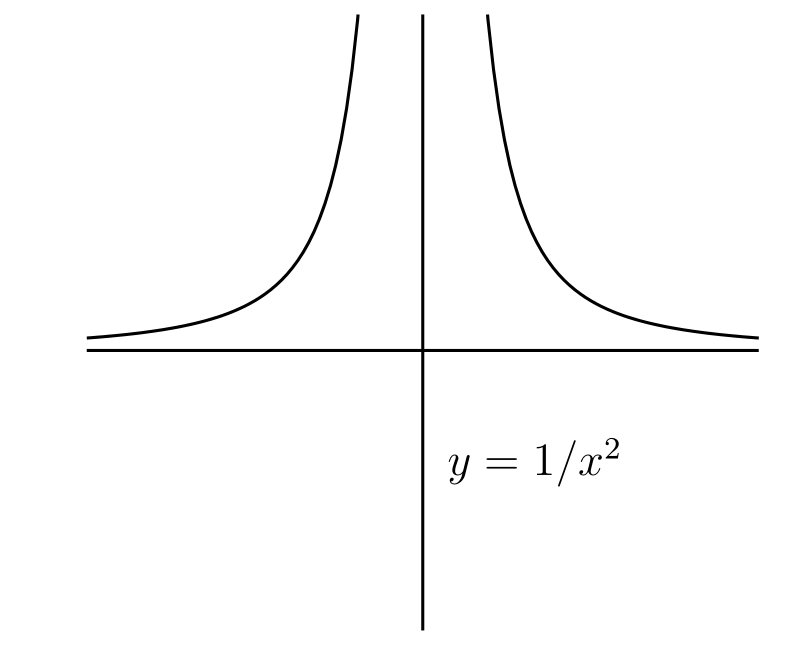
\(y = 1/x,\ y = 1/x^{2},\ y = 1/x^{3},\ \ldots\) のグラフを描け。

[最初の二つの関数のグラフを次の図に示す。\(1/0,\ 1/0^{2},\ \ldots\) といった表現は意味をなさないので、これらの関数は \(x = 0\) で定義されないことに注意してほしい]

\(y = x + (1/x),\ x - (1/x),\ x^{2} + (1/x^{2}),\ x^{2} - (1/x^{2}),\ ax + (b/x)\) が通る点を調べよ。正の値、負の値、\(a,\ b\) など様々な値を試すこと。

次の関数の通る点を調べよ: \[ y = \frac{x + 1}{x - 1},\quad \left(\frac{x + 1}{x - 1}\right)^{2},\quad \frac{1}{(x - 1)^{2}},\quad \frac{x^{2} + 1}{x^{2} - 1} \]

\(y = 1/(x - a)(x - b),\ 1/(x - a)(x - b)(x - c)\) の通る点を調べよ。ただし \(a \lt b \lt c\) とする。

\(m\) が極端に大きいときの曲線 \(y = 1/x^{m}\) の一般的な形を示せ。\(m\) が偶数の場合と奇数の場合を分けて考えること。