第三章 複素数
§34 平面上の直線に沿った変位
ここまでの二つの章で考えてきた「実数」は、様々な視点から捉えることができる。実数を幾何学的な意味を持たない純粋な数と捉えることもできるし、幾何学的な意味を持たせるにしてもその方法は少なくとも三つある。まず実数を長さの表現、つまり第一章で考えた基準直線 \(\Lambda\) に沿った長さ \(A_{0}P\) とみなす方法がある。次に実数を点の別名、つまり \(A_{0}\) からの距離が \(x\) である点 \(P\) を表すとみなす方法がある。そして実数を \(\Lambda\) 上における変位の表現つまり位置の変化量とみなす方法がある。ここでは最後の考え方についてさらに考える。
直線 \(\Lambda\) 上の点 \(P\) に置かれた小さい粒子が点 \(Q\) に移動したとする。このとき粒子を \(P\) から \(Q\) に移動させるのに必要な位置の差分あるいは位置の変動を変位 (displacement) \(\bm{\overline{PQ}}\) と呼ぶ。粒子の位置の変動を完全に記述するには、次の三つの要素が必要になる: 変位の量、直線に沿って前か後ろという変位の向き、そして変位を適用する点である。しかし粒子の移動による位置の変化だけを考えるなら、変位を適用する点を無視して、同じ長さと向きを持つ変位を同一視した方が自然である。すると変位はその長さ \(PQ = x\) と \(x\) の符号で表される向きによって完全に決定されるので、変位 \(\bm{[x]}\) と表現しても曖昧さは生じない1ことになる。よって \(\overline{PQ} = [x]\) と書いても問題ない。
鍵括弧を使って長さおよび数字 \(x\) と変位 \([x]\) を区別する2。もし \(P\) の座標が \(a\) なら、\(Q\) の座標は \(a + x\) となる。そして変位 \([x]\) は点 \(a\) にある粒子を点 \(a + x\) まで移動させる。
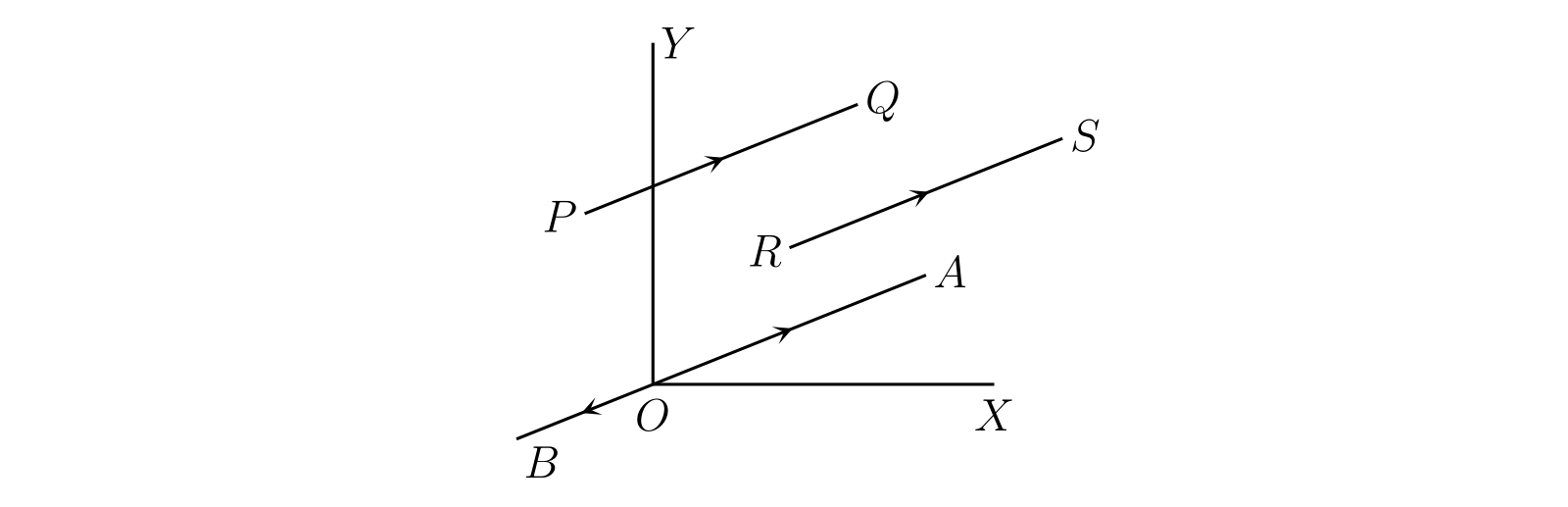
次に平面上の変位を考える。直線上の変位と同様に平面上の変位 \(\overline{PQ}\) を定義するが、変位を完全に特定するために必要な情報が増える。必要な情報は四つある: (i) 変位の量、すなわち直線 \(PQ\) の長さ、(ii) 変位の方向、すなわち平面上に固定された直線と \(PQ\) がなす角度、(iii) 変位の向き、そして (iv) 適用する点である。同じ長さ・方向・向きを持つ変位を同一視するなら、もちろん四つ目は無視できる。つまり \(PQ\) と \(RS\) の長さが同じで、平行で、\(P\) から \(Q\) への運動の向きと \(R\) から \(S\) への運動の向きが同じなら、変位 \(\overline{PQ}\) と変位 \(\overline{PQ}\) は同一だとみなし、次のように表記する: \[ \overline{PQ} = \overline{RS} \]
平面上に座標軸の組を (図 19 の \(OX,\ OY\) のように) 取る。\(PQ\) と同じ長さで平行な直線 \(OA\) を、\(O\) から \(A\) の向きが \(P\) から \(Q\) の向きと同じになるように取る。すると \(\overline{PQ}\) と \(\overline{OA}\) は同じ変位となる。\(x\) と \(y\) を \(A\) の座標とすると、\(\overline{OA}\) は \(x\) と \(y\) で曖昧さなく特定できる。\(\overline{OA}\) を変位 \(\bm{[x, y]}\) と呼び、次のように表記する: \[ \overline{OA} = \overline{PQ} = \overline{RS} = [x, y] \]
§35 変位の同値性および実数との積
前節の設定で \(P\) の座標が \((\xi, \eta)\) で \(Q\) の座標が \((\xi', \eta')\) なら、次の式が直ちに分かる: \[ x = \xi' - \xi,\quad y = \eta' - \eta \] つまり \((\xi, \eta)\) から \((\xi', \eta')\) への変位は次のように表記できる: \[ [\xi' - \xi, \eta' - \eta] \]
二つの変位 \([x, y],\ [x', y']\) は \(x = x'\) かつ \(y = y'\) のとき等しく、等しいのはこの場合に限る。よって \([x, y] = [x', y']\) が成り立つための必要十分条件が分かる: \[ x = x',\quad y = y' \qquad \text{(1)} \]
\(\overline{PQ}\) の逆の変位 \(\overline{QP}\) は \([\xi - \xi', \eta - \eta']\) であり、次のように定めるのが自然である: \[ \begin{aligned} [\xi - \xi', \eta - \eta'] & = -[\xi' - \xi, \eta' - \eta],\\ \overline{QP} & = -\overline{PQ} \end{aligned} \] この二つの式が \(-[\xi' - \xi, \eta' - \eta],\ -\overline{PQ}\) という表記の意味を定義する。こうして \[ -[x, y] = [-x, -y] \] を定義したなら、続いて符号を問わない任意の実数 \(\alpha\) について \[ \alpha[x, y] = [\alpha x, \alpha y] \qquad \text{(2)} \] と自然に定義できる。この定義を使えば、図 19 で \(OB = -\frac{1}{2}OA\) とき次が成り立つと分かる: \[ \overline{OB} = -\frac{1}{2}\overline{OA} = -\frac{1}{2}[x, y] = [-\frac{1}{2}x, -\frac{1}{2}y] \]
方程式 (1) と (2) は、変位の同値性と変位と実数の乗算という変位に関する二つの重要な概念を表している。
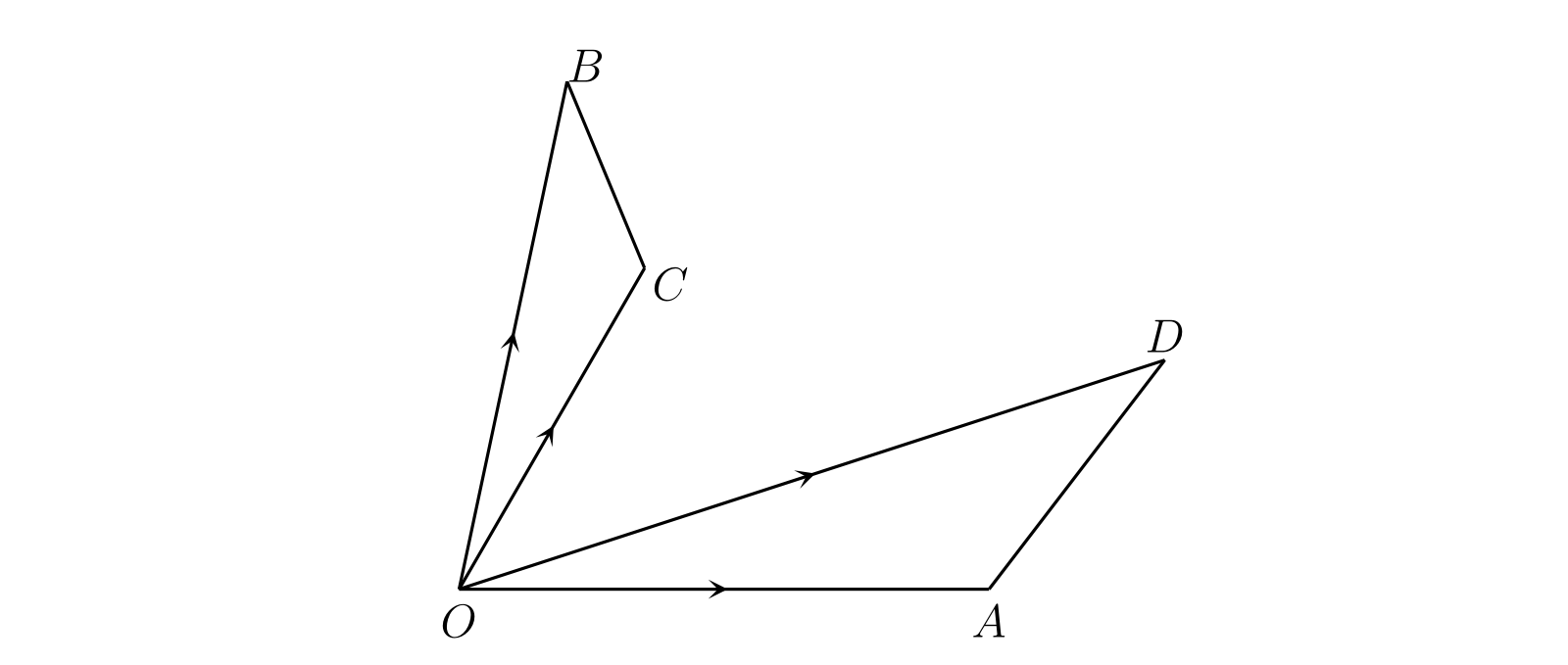
§36 変位の加算
次の式にはまだ意味が与えられていない: \[ \overline{PQ} + \overline{P'Q'},\quad [x, y] + [x', y'] \] 常識的に考えて、二つの変位の和はそれらを連続して適用したときの結果を表す変位として定義される必要がある。\(P'Q'\) と長さが同じで平行な \(QQ_{1}\) を書く。\(P\) に対して \(\overline{PQ}\) と \(\overline{P'Q'}\) を連続して適用すると、\(P\) はまず \(Q\) に移動しその後 \(Q_{1}\) に移動する。よって \(\overline{PQ}\) と \(\overline{P'Q'}\) の和は \(\overline{PQ_{1}}\) として定義するべきと分かる。\(PQ\) と長さが同じで平行な \(OA\)、および \(P'Q'\) と長さが同じで平行な \(OB\) を書いて平行四辺形 \(OACB\) を完成させれば、次が成り立つ: \[ \overline{PQ} + \overline{P'Q'} = \overline{PQ_{1}} = \overline{OA} + \overline{OB} = \overline{OC} \]
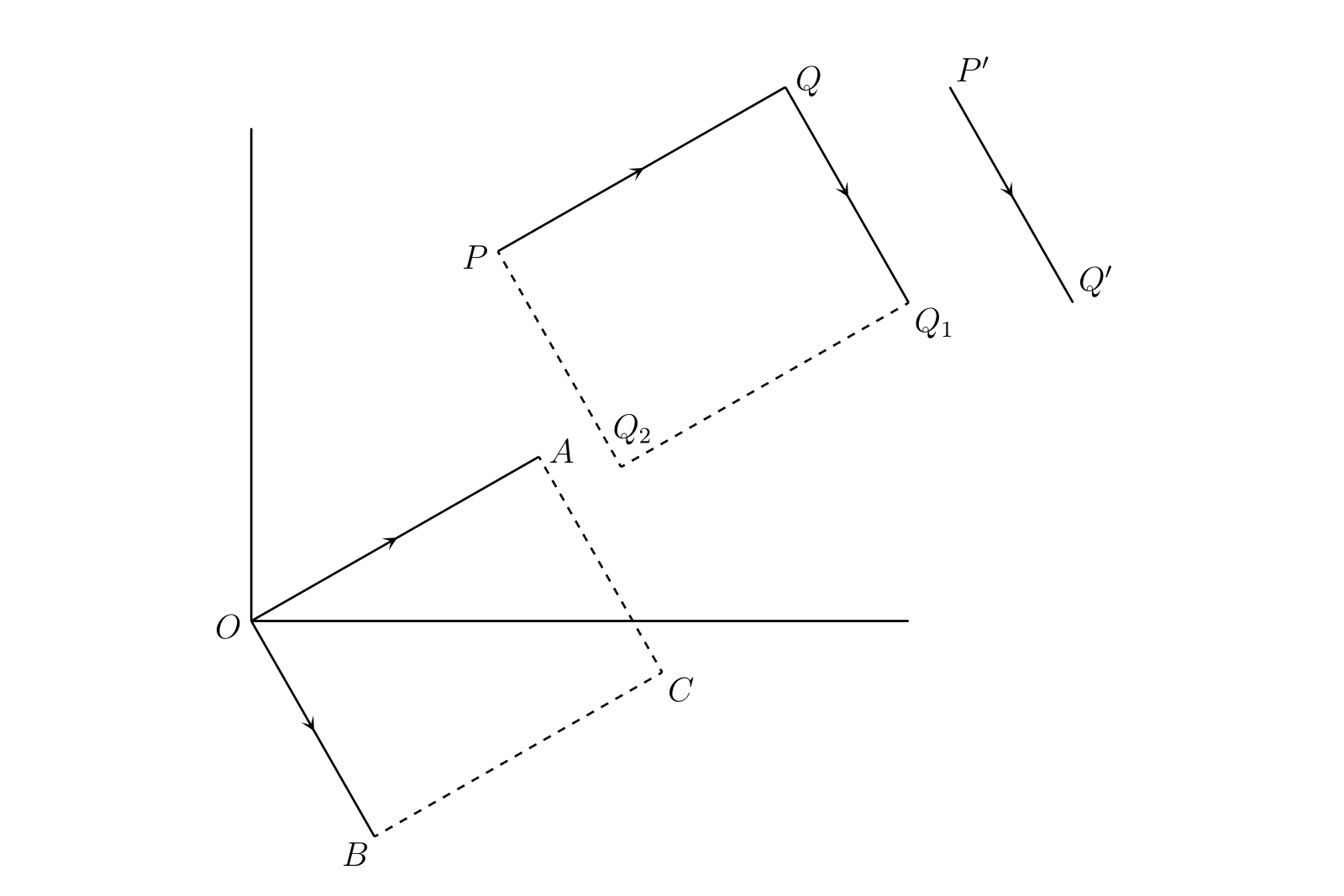
この定義から導かれることを考える。\(B\) の座標が \(x', y'\) なら、\(AB\) の中点の座標は \((\frac{1}{2}(x + x'),\ \frac{1}{2} (y + y'))\)、\(C\) の座標は \((x + x',\ y + y')\) となる。よって \[ [x, y] + [x', y'] = [x + x', y + y'] \qquad \text{(3)} \] が成り立つ。これは変位の和の記号による定義ともみなせる。さらに \[ \begin{aligned} [x', y'] + [x, y] & = [x' + x, y' + y] \\ & = [x + x', y + y'] \\ & = [x, y] + [x', y'] \end{aligned} \qquad \text{(4)} \] も成り立つ。つまり通常の代数における等式 \(a + b = b + a\) と同様に変位の和は交換法則を満たす。\(P\) を最初に \(P'Q'\) と同じ方向と長さだけ移動させ、それから \(PQ\) と同じ方向と長さだけ移動させた場合にも \(P\) が \(Q_{1}\) に到達するというのは幾何学的に明らかであり、変位の交換法則がこの事実を表していると言える。
変位の減算を次のように定義する: \[ [x, y] - [x', y'] = [x, y] + (-[x', y']) \qquad \text{(5)} \] これは \([x, y] + [-x', -y']\) および \([x - x', y - y']\) と同じことである。特に次が成り立つ: \[ [x, y] - [x, y] = [0, 0] \]
変位 \([0, 0]\) は粒子を移動させない。これはゼロ変位 (zero displacement) であり、\([0, 0] = 0\) と表記する。
-
次の等式を示せ:
- \(\alpha [\beta x, \beta y] = \beta [\alpha x, \alpha y] = [\alpha \beta x, \alpha \beta y]\)
- \(([x, y] + [x', y']) + [x'', y''] = [x, y] + ([x', y'] + [x'', y''])\)
- \([x, y] + [x', y'] = [x', y'] + [x, y]\)
- \((\alpha + \beta) [x, y] = \alpha [x, y] + \beta [x, y]\)
- \(\alpha \{[x, y] + [x', y']\} = \alpha [x, y] + \alpha [x', y']\)
[(iii) は前に示した。他の等式も定義から容易に従う。(iii) に対して行ったような幾何学的な意味の考察をそれぞれのケースについて行うこと]
-
\(M\) が \(PQ\) の中点なら \(\overline{OM} = \frac{1}{2}(\overline{OP} + \overline{OQ})\) が成り立つ。一般的に言えば、\(M\) が \(PQ\) を \(\mu : \lambda\) の比に分割するとき、次の式が成り立つ: \[ \overline{OM} = \frac{\lambda}{\lambda + \mu}\, \overline{OP} + \frac{\mu}{\lambda + \mu}\, \overline{OQ} \]
-
\(G\) が同一の粒子 \(P_{1},\ P_{2},\ \ldots,\ P_{n}\) の重心なら、次の式が成り立つ: \[ \overline{OG} = \frac{\overline{OP_{1}} + \overline{OP_{2}} + \cdots + \overline{OP_{n}}}{n} \]
-
\(P,\ Q,\ R\) を同一直線上にある点とすると、\(0\) でない実数 \(\alpha,\ \beta,\ \gamma\) を使って次のように書ける: \[ \alpha · \overline{OP} + \beta · \overline{OQ} + \gamma · \overline{OR} = 0 \] 加えて逆も成り立つ。 [これは問題 2 の言い換えに過ぎない]
-
\(\overline{AB}\) と \(\overline{AC}\) が同一直線上にない二つの変位で \[ \alpha · \overline{AB} + \beta · \overline{AC} = \gamma · \overline{AB} + \delta · \overline{AC} \] が成り立つなら、\(\alpha = \gamma\) かつ \(\beta = \delta\) である。
[\(AB_{1} = \alpha · AB,\ AC_{1} = \beta · AC\) を取り、平行四辺形 \(AB_{1}P_{1}C_{1}\) を完成させる。すると \(\overline{AP_{1}} = \alpha · \overline{AB} + \beta · \overline{AC}\) が成り立つ。この形を使った \(\overline{AP_{1}}\) の表現方法は一通りしかないことが分かるので、命題が示せる]
-
\(ABCD\) を平行四辺形とする。平行四辺形内部の点 \(Q\) を取り、直線 \(RQS\) と \(TQU\) を辺に平行に取る。\(RU\) と \(TS\) が \(AC\) 上で交わることを示せ。
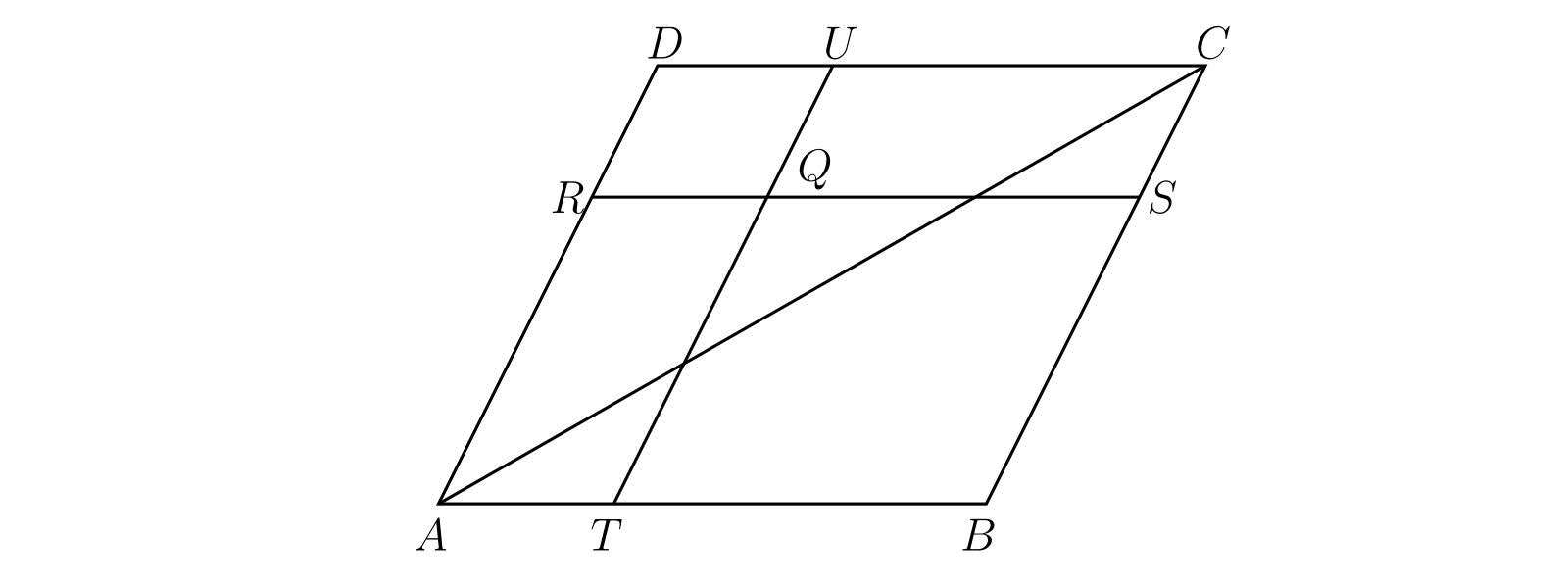 図 21
図 21[比 \(AT:AB\) と \(AR:AD\) を \(\alpha\) と \(\beta\) で表す。このとき次が成り立つ: \[ \begin{gathered} \overline{AT} = \alpha · \overline{AB},\quad \overline{AR} = \beta · \overline{AD}, \\ \overline{AU} = \alpha · \overline{AB} + \overline{AD},\quad \overline{AS} = \overline{AB} + \beta · \overline{AD} \end{gathered} \]
\(RU\) と \(AC\) の交点を \(P\) とすると、三点 \(R,\ U,\ P\) は同一直線上にあるので \[ \overline{AP} = \frac{\lambda}{\lambda + \mu}\, \overline{AR} + \frac{\mu}{\lambda + \mu}\, \overline{AU} \] が成り立つ。ここで \(P\) は \(RU\) を \(\mu : \lambda\) に分割する。ここから次の式が分かる: \[ \overline{AP} = \frac{\alpha\mu}{\lambda + \mu}\, \overline{AB} + \frac{\beta\lambda + \mu}{\lambda + \mu}\, \overline{AD}. \]
一方 \(P\) は \(AC\) 上にあるので、\(\overline{AP}\) は \(\overline{AC}\) の実数倍である。つまり \[ \overline{AP} = k · \overline{AC} = k · \overline{AB} + k · \overline{AD} \] と書ける。よって (問題 5 から) \(\alpha\mu = \beta\lambda + \mu = (\lambda + \mu)k\) が分かり、この式から \[ k = \frac{\alpha\beta}{\alpha + \beta - 1} \] が求まる。この結果の対称性から、\(TS\) と \(AC\) の交点を \(P'\) とすれば同様の議論で \[ \overline{AP'} = \frac{\alpha\beta}{\alpha + \beta - 1}\, \overline{AC} \] が分かる。よって \(P\) と \(P'\) は同一の点を表す]
-
\(ABCD\) を平行四辺形、\(M\) を \(AB\) の中点とする。\(DM\) が \(AC\) を三等分し、\(AC\) が \(DM\) を三等分することを示せ3。
§37 変位の乗算
ここまでは二つの変位の積が持つ意味について考えてこなかった。考えた唯一の積は変位と数値の乗算である。式 \[ [x, y] × [x', y'] \] は意味を持たず、この意味は好きに定義できる。しかし明らかに、定義が少しでも使いものになるためには、二つの変位の積が変位となる必要がある。
積の定義の一例として \[ [x + x', y + y'] \] が考えられる。言い換えると、二つの変位の積を和と同じものとして定義するのである。しかしこの定義には二つの深刻な欠点がある。第一に、この定義には意味がない。以前から表現できているのものを表現する別の方法をわざわざ追加することになる。第二に、次の理由によりこの定義は不便かつミスリーディングとなる。\(\alpha\) が実数なら \(\alpha [x, y]\) は \([\alpha x, \alpha y]\) だと定義した。また §34 で見たように、実数 \(\alpha\) 自身も変位とみなせる: 軸 \(OX\) に沿った変位 \([\alpha]\)、後で定義した記法を使えば変位 \([\alpha, 0]\) である。よって積の定義が次の等式を満たすことが (絶対に必要ではないにせよ) 望ましい: \[ [\alpha, 0] [x, y] = [\alpha x, \alpha y] \] 和と同じ積の定義ではこれが成り立たない。
次の定義なら多少ましと思うかもしれない: \[ [x, y] [x', y'] = [xx', yy'] \] しかしこの定義だと \[ [\alpha, 0] [x, y] = [\alpha x, 0] \] となり、二つ目の欠点を払拭できない。
実は、積 \([x, y] [x', y']\) に与えるのに最も適した意味が何なのかは決して自明でない。確かなのは次の三つである。(1) 定義が役に立つためには、この変位の積も座標が \(x\) と \(y\) から決まる変位となる、つまり \[ [x, y] [x', y'] = [X, Y] \] と書いたときに \(X\) と \(Y\) が \(x,\ y,\ x',\ y'\) の関数となる必要がある。(2) 定義は等式 \[ [x, 0] [x', y'] = [xx', xy'] \] を満たす必要がある。(3) 定義は通常の積と同じ交換法則・分配法則・結合法則、つまり次の等式を満たす必要がある: \[ \begin{aligned} [x, y] [x', y'] & = [x', y'] [x, y],\\ ([x, y] + [x', y']) [x'', y''] & = [x, y] [x'', y''] + [x', y'] [x'', y''],\\ [x, y] ([x', y'] + [x'', y'']) & = [x, y] [x', y'] + [x, y] [x'', y''],\\ [x, y] ([x', y'] [x'', y'']) & = ([x, y] [x', y']) [x'', y''] \end{aligned} \]
§38 変位の積の正しい定義
採用すべき正しい定義は次の通りである。\(\triangle OAB\) と \(\triangle OCD\) を対応する角度がこの順番の相似な三角形とする。このとき \[ OB/OA = OD/OC \] および \(OB · OC = OA · OD\) が成り立つ。ここから次に示す変位の乗算と除算の定義が提案される: \[ \overline{OB}/\overline{OA} = \overline{OD}/\overline{OC},\quad \overline{OB} · \overline{OC} = \overline{OA} · \overline{OD} \]
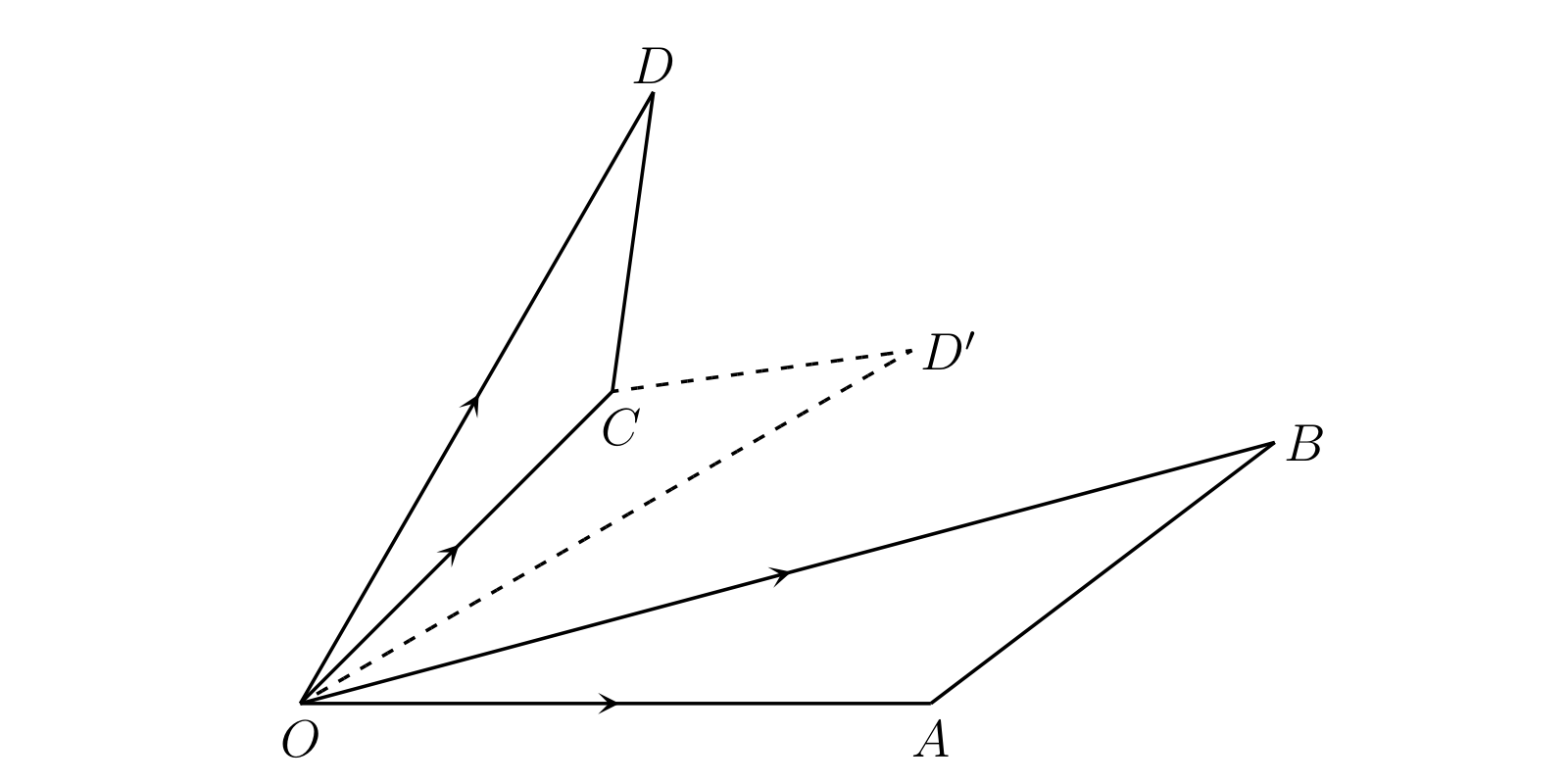
ここで \[ \overline{OB} = [x, y],\quad \overline{OC} = [x', y'],\quad \overline{OD} = [X, Y] \] として、\(A\) を点 \((1, 0)\) と仮定する。すると \(\overline{OA} = [1, 0]\) であり、 \[ \overline{OA} · \overline{OD} = [1, 0] [X, Y] = [X, Y] \] および \[ [x, y] [x', y'] = [X, Y] \] が成り立つ。つまり積 \(\overline{OB} · \overline{OC}\) を \(\overline{OD}\) と定義すれば、\(D\) は \(OC\) 上に \(\triangle OAB\) と相似な三角形を作ったときの頂点となる。ただし定義に曖昧さがあり、\(OC\) から作れる三角形が (\(\triangle OCD\) と \(\triangle OCD'\) の) 二つある点に注意が必要となる。ここでは \(\angle COD\) と \(\angle AOB\) が向きも含めて等しくなるように選ぶ。このとき二つの三角形は向きを含めて相似であると言う。
\(B\) と \(C\) の極座標がそれぞれ \((\rho, \theta)\) と \((\sigma, \phi)\) なら、 \[ x = \rho\cos\theta,\quad y = \rho\sin\theta,\quad x' = \sigma\cos\phi,\quad y' = \sigma\sin\phi \] が成り立つ。このとき \(D\) の極座標は \((\rho\sigma, \theta + \phi)\) なので、 \[ \begin{alignedat}{3} X & = \rho\sigma\cos(\theta + \phi) & & = xx' - yy',\\ Y & = \rho\sigma\sin(\theta + \phi) & & = xy' + yx' \end{alignedat} \] が分かる。よって定義は次のように表せる: \[ [x, y] [x', y'] = [xx' - yy', xy' + yx'] \qquad \text{(6)} \]
この定義は必要とされる通り (1) \(y = 0\) なら \(X = xx',\ Y = xy'\) となる。さらに (2) 右辺は \(x\) と \(x'\) および \(y\) と \(y'\) を入れ替えても変わらず \[ [x, y] [x', y'] = [x', y'] [x, y] \] であることも確認できる。また (3) 次の式も成り立つ: \[ \begin{aligned} \{[x, y] + [x', y']\} [x'', y''] & = [x + x', y + y'] [x'', y'']\\ & = [(x + x') x'' - (y + y') y'', (x + x') y'' + (y + y') x'']\\ & = [xx'' - yy'', xy'' + yx''] + [x'x'' - y'y'', x'y'' + y'x'']\\ & = [x, y] [x'', y''] + [x', y'] [x'', y''] \end{aligned} \]
同様に §37 の最後であげた等式は全て確認できる。よって定義 (6) は §37 で示した要件を全て満たす。
変位の積が交換法則、分配法則、結合法則を満たすことを、上述の幾何学的な定義から直接示せ。 [例として交換法則を示す。\(\overline{OB}\) と \(\overline{OC}\) の積は \(\overline{OD}\) で、\(\triangle COD\) は \(\triangle AOB\) と相似である (図 22)。\(\overline{OC} · \overline{OB}\) を得るには、\(OB\) 上に \(\triangle AOC\) と相似な \(\triangle BOD_{1}\) を取る。後は \(D\) と \(D_{1}\) が等しいこと、つまり \(\triangle BOD\) と \(\triangle AOC\) が相似なことを証明すればよい。これは簡単な初等幾何学の問題である]
§39 複素数 (その 1)
\(OX\) に沿った変位 \([x]\) が点 \((x)\) と実数 \(x\) に対応したように、平面上の変位 \([x, y]\) にも対応する点 \((x, y)\) と実数の組 \(\bm{x,\ y}\) が存在する。
この実数の組 \(x,\ y\) を次のように表記すると便利である: \[ x + yi \] こう表記する理由は後で明らかになる。今は \(x + yi\) を \(\bm{[x, y]}\) の別表記に過ぎないと考えてなくてはならない。\(x + yi\) を複素数 (complex number) と呼ぶ。
次に複素数の同一性、加算、乗算を定義する。任意の複素数には対応する変位が一つ存在する。二つの複素数が同一なのは対応する変位が同一なときと定め、二つの複素数の和および積は対応する変位の和または積に対応する複素数と定める。つまり \[ x + yi = x' + y'i \qquad \text{(1)} \] は \(x = x',\ y = y'\) と同値であり、さらに次が成り立つ: \[ (x + yi) + (x' + y'i) = (x + x') + (y + y')i \qquad \text{(2)} \] \[ (x + yi) (x' + y'i) = xx' - yy' + (xy' + yx')i \qquad \text{(3)} \]
(2) と (3) の特殊ケースとして、次が成り立つ: \[ x + yi = (x + 0i) + (0 + yi) \] \[ (x + 0i) (x' + y'i) = xx' + xy'i \] この式は、複素数を扱うとき \(x + 0i\) の代わりに \(x\)、あるいは \(0 + yi\) の代わりに \(yi\) と書いても問題は起きないことを示している。これからは私たちもこう表記する。
複素数の整数乗と複素数の多項式は初等代数と同様に定義される。例えば (3) で \(x = x',\ y = y'\) とすれば次のようになる: \[ (x + yi)^{2} = (x + yi) (x + yi) = x^{2} - y^{2} + 2xyi \]
複素数の加算と乗算が次の式で表される代数法則を満たすことは簡単に確認できる: \[ \begin{aligned} (x + yi) + (x' + y'i) & = (x' + y'i) + (x + yi)\\ \{(x + yi) + (x' + y'i)\} + (x'' + y''i) & = (x + yi) + \{(x' + y'i) + (x'' + y''i)\}\\ (x + yi) (x' + y'i) & = (x' + y'i) (x + yi)\\ (x + yi)\{(x' + y'i) + (x'' + y''i)\} & = (x + yi)(x' + y'i) + (x + yi)(x'' + y''i)\\ \{(x + yi) + (x' + y'i)\}(x'' + y''i) & = (x + yi)(x'' + y''i) + (x' + y'i)(x'' + y''i)\\ (x + yi) \{(x' + y'i) (x'' + y''i)\} & = \{(x + yi) (x' + y'i)\} (x'' + y''i) \end{aligned} \] これらの証明は対応する変位に対する式の証明と本質的に同一である。
複素数の減算と除算は初等代数と同様に定義される。つまり \((x + yi) - (x' + y'i)\) の定義は \[ (x + yi) + \{- (x' + y'i)\} = x + yi + (-x' - y'i) = (x - x') + (y - y')i \] となる。あるいは次の式を満たす複素数 \(\xi + \eta i\) を定義としても構わない: \[ (x' + y'i) + (\xi + \eta i) = x + yi \] どちらを選んでも結果は変わらない。\((x + yi)/(x' + y'i)\) は次の式を満たす複素数 \(\xi + \eta i\) として定義される: \[ (x' + y'i) (\xi + \eta i) = x + yi \] 書き換えると \[ x' \xi - y' \eta + (x' \eta + y' \xi)i = x + yi \] となり、さらに変形すれば次の等式を得る: \[ x' \xi - y' \eta = x,\quad x' \eta + y' \xi = y \qquad \text{(4)} \]
この方程式を \(\xi\) と \(\eta\) について解くと \[ \xi = \frac{xx' + yy'}{{x'}^{2} + {y'}^{2}},\quad \eta = \frac{yx' - xy'}{{x'}^{2} + {y'}^{2}} \] が得られる。この解は \(x'\) と \(y'\) が両方 \(0\) のとき、つまり \(x' + y'i = 0\) のとき意味をなさない。そのため減算はいつでも行えるが、除算は割る数が \(0\) でないときのみ行える。
-
幾何学的に考えると、\(\overline{OB}\) を \(\overline{OC}\) で割る変位の除算は \(\triangle COB\) と \(\triangle AOD\) が相似になる \(D\) を見つける問題とみなせる。これは \(C\) が \(0\) と等しく \(\overline{OC} = 0\) である場合を除けば可能なことが示せる。
-
\(x + yi\) と \(x - yi\) は共役 (conjugate) であると言う。次の式を確認せよ: \[ (x + yi)(x - yi) = x^{2} + y^{2} \] つまり共役な二つの複素数の積は実数である。さらに次の式も示せ: \[ \begin{aligned} \frac{x + yi}{x' + y'i} & = \frac{(x + yi)(x' - y'i)}{(x' + y'i)(x' - y'i)} \\ & = \frac{xx' + yy' + (x'y - xy')i}{{x'}^{2} + {y'}^{2}} \end{aligned} \]
§40 複素数 (その 2)
最も重要な実数の性質の一つが、二つの数の積が \(\bm{0}\) となるのは少なくとも一方が \(\bm{0}\) のときに限るという因数定理 (factor theorem) である。複素数でもこれが正しいことを証明するために、前節の式 (4) に \(x = 0\) と \(y = 0\) を代入する。すると \[ x'\xi - y'\eta = 0,\quad x'\eta + y'\xi = 0 \] が成り立つ。この方程式から \(\xi = 0,\ \eta = 0\) つまり \[ \xi + \eta i = 0 \] が成り立つか、そうでなければ \(x' = 0\) かつ \(y' = 0\) つまり \(x' + y'i = 0\) が成り立つことが分かる。よって \(x' + y'i\) と \(\xi + \eta i\) のどちらかが \(0\) でない限り \(x + yi\) は \(0\) にならない。
§41 方程式 \(i \times i = -1\)
\(x + 0i\) を \(x\) と表記し、\(0 + yi\) を \(yi\) と表記すると前に定めた。さらに複素数 \(1i\) を \(i\) と表記するとしよう。\(i\) は \(OY\) に沿った単位量の変位に対応する複素数であり、 \[ i^{2} = ii = (0 + 1i) (0 + 1i) = (0 · 0 - 1 · 1) + (0 · 1 + 1 · 0)i = -1 \] つまり \((-i)^{2} = -1\) が成り立つ。よって \(i\) と \(-i\) は方程式 \(x^{2} = -1\) を満たす。
ここまでくれば、次のことを容易に納得できるだろう: 複素数の加算と乗算は、\(\bm{i}\) を実数を表す記号として実数と同様に扱い、計算結果に含まれる \(\bm{ii = i^{2}}\) を \(\bm{-1}\) に変えれば計算できる。例えば次のようになる: \[ \begin{aligned} (x + yi) (x' + y'i) & = xx' + xy'i + yx'i + yy'i^{2}\\ & = (xx' - yy') + (xy'+ yx')i \end{aligned} \]
§42 \(i\) による乗算の幾何学的解釈
等式 \[ (x + yi)i = -y + xi \] が成り立つから、\(x + yi\) が \(\overline{OP}\) に対応するとき \(\angle POQ\) が正の直角になるよう \(Q\) を取ると、\((x + yi)i\) が \(\overline{OQ}\) に対応する。言い換えると、複素数 \(\bm{i}\) による乗算は変位を直角に回転させる。
この考えに基づいて複素数の理論を構築することもできる。\(x\) が \(OX\) 方向の変位を表し、\(i\) を \(x\) を直角に回転させる操作を表すとすれば、量が \(y\) の \(OY\) 方向の変位を \(yi\) と表記することになる。そうすれば \(x + yi\) は §37–§40 と同様に自然に定義され、\((x + yi)i\) は \(x + yi\) を直角に回転させた変位を表す。さらに \((x + yi)x'\) は \(xx' + yx'i\)、\((x + yi)y'i\) は \(-yy' + xy'i\) となり、\((x + yi) (x' + y'i)\) はこれらの和として次のように定義されていただろう: \[ xx' - yy' + (xy' + yx')i \]
§43 実係数の二次方程式
\(z^2 + 1 = 0\) を満たす実数 \(z\) は存在しない。この事実を「方程式は実根を持たない」と表現する。しかし先ほど見た通り、\(i\) と \(-i\) という二つの複素数はこの方程式を満たす。この事実を「方程式は二つの複素根を持つ」と表現する。\(z^{2} = -1\) を満たすこの \(i\) を \(\sqrt{-1}\) と表記する場合がある。
複素数は虚数 (imaginary number) とも呼ばれる4。ただしこう呼ばれているからといって、通常の言葉の意味で虚数が実数よりも「虚 (imaginary)」である、あるいは虚数が数字でないなどと納得してはいけない。ここまでの議論から分かるように、二つの記号を並べて表記される実数の組 \(\bm{(x, y)}\) を、考える上で便利なように \(x + yi\) と表記したのが虚数である。この実数の組の「リアルさ」は、\(\frac{1}{2}\) といった通常の数字、それが印刷された紙、あるいは太陽系の「リアルさ」と全く変わらない。例えば \[ i = 0 + 1i \] は数字の組 \((0, 1)\) の別表記であり、点あるいは変位 \([0, 1]\) として幾何学的に表すこともできる。あるいは \(i\) が方程式 \(z^{2} + 1 = 1\) の根だと言った場合、それは数字の組 (あるいは変位) を組み合わせる「乗算」という操作が定義されていて、二つの \((0, 1)\) をその操作で組み合わせたときの結果が \((-1, 0)\) になる、ということを意味している。
より一般的な次の方程式を考える: \[ az^{2} + 2bz + c = 0 \] ここで \(a,\ b,\ c\) は実数である。\(b^{2} \gt ac\) なら、通常の解の公式で二つの実根が求まる: \[ \frac{-b ± \sqrt{b^{2} - ac}}{a} \] \(b^{2} \lt ac\) のときこの方程式は実根を持たない。しかし \[ \left\{z + \left(\frac{b}{a}\right)\right\}^{2} = -\frac{ac - b^{2}}{a^{2}} \] であり、\(z + (b/a)\) を \(±i\sqrt{ac - b^{2}}/a\) とすればこの式は満たされる5。よってこの方程式には次の二つの複素根があると言う: \[ \frac{-b ± i\sqrt{ac - b^{2}}}{a} \]
\(b^{2} = ac\) のとき (方程式が \(x = -b/a\) でのみ成り立つとき) この方程式は二つの等しい根があると言うことにすれば、実係数の二次方程式はどんなときにも二つの根 (二つの異なる実根・二つの等しい実根・二つの異なる複素根のどれか) を持つとみなせる。
複素根を認めた場合に二次方程式が二つより多い根を持ちうるか、という疑問が自然に生じる。この答えは否であり、それは簡単に示せる。この証明の格子は初等代数において \(n\) 次方程式が最大でも \(n\) 個の実根を持つことの証明に使ったものと同じである。\(z = x + yi\) として複素数 \(x + yi\) を \(z\) という一文字で表す。\(f(z)\) を任意の \(z\) の多項式とし、その係数は実数でも複素数でもあり得るとする。証明は次の命題を順に示す:
- \(a\) を実数または複素数とすると、\(f(z)\) を \(z - a\) で割ったときの余りは \(f(a)\) である
- \(a\) が方程式 \(f(z) = 0\) の根なら \(f(z)\) は \(z - a\) で割り切れる
- もし \(f(z)\) の次数が \(n\) で \(f(z) = 0\) が \(n\) 個の根 \(a_{1},\ a_{2},\ \ldots,\ a_{n}\) を持つなら、 \[ f(z) = A(z - a_{1}) (z - a_{2}) \cdots (z - a_{n}) \] が成り立つ。ここで \(A\) は実数または複素数の定数であり、具体的には \(f(z)\) における \(z^{n}\) の係数である。
この結果と §40 の定理を合わせれば、\(f(z)\) の根が \(n\) 個以下であると分かる。
実係数の二次方程式にはちょうど二つの根があると分かった。これが係数が実数でも複素数でもあり得る任意の次数の方程式についても正しいことを後で見る: つまり指数が \(\bm{n}\) の方程式はちょうど \(\bm{n}\) 個の根を持つ。この証明で唯一の障害となるのは最初の部分、つまり任意の多項式が少なくとも一つの根を持つことを示す部分である。証明の詳細は後回しにする6。しかしこの定理から得られる非常に興味深い結果についてここで触れておく。私たちは数の理論を正の整数とそれに対する加算と乗算から始めて減算と除算を定義し、この演算が常に行えるためには新しい種類の数を認めなければならないことを見た。例えば \(3 - 7\) に意味を持たせるには負の数を認める必要があり、\(\frac{3}{7}\) の意味付けには有理数が必要だった。さらに根号や方程式の解として表される数を考えるために代数演算のリストを拡張するたびに、数の概念を広げない限り不可能な操作が生まれてしまうのを見た。例えば第一章では、完全平方数でない数 (\(2\) など) の平方根を考えるために無理数の存在を認めた。
\(-1\) の平方根を取るといった操作のためには数の概念のさらなる拡張が必要であり、この章では複素数の存在を認めた。とすれば、次数の高い方程式の中には複素数でも解けないものがあるのではないか、そして超複素数とでも呼ぶべき高階の数を次々と作れるのではないかと思っても不思議ではない。しかし任意の代数方程式の根が複素数であるという事実から、これは正しくない。通常の代数演算のどれを複素数に行っても、得られるのは複素数だけである。これを専門用語で「複素数の体は代数演算について閉じている」と言う。
他の話題に移る前に、加算と乗算の規則だけを使って示せる初等代数の定理は全て、数が実数であっても複素数であっても正しいことを付け加えておく。代数の規則は実数だけではなく複素数にも通用するからである。例えば \(\alpha\) と \(\beta\) が \[ az^{2} + 2bz + c = 0 \] の根なら、次が成り立つ: \[ \alpha + \beta = -(2b/a),\quad \alpha\beta = (c/a) \]
同様に \(\alpha,\ \beta,\ \gamma\) が \[ az^{3} + 3bz^{2} + 3cz + d = 0 \] の根なら \[ \alpha + \beta + \gamma = -(3b/a),\quad \beta\gamma + \gamma\alpha + \alpha\beta = (3c/a),\quad \alpha\beta\gamma = -(d/a) \] となる。こういった定理は \(a,\ b,\ \ldots,\ \alpha,\ \beta,\ \ldots\ \) が実数でも複素数でも成り立つ。
§44 アルガン図
図 24 で \(P\) を点 \((x, y)\) とし、\(r\) を \(OP\) の長さ、\(\theta\) を \(\angle XOP\) とすると次が成り立つ: \[ x = r\cos\theta,\quad y = r\sin\theta,\quad r = \sqrt{x^{2} + y^{2}},\quad \cos\theta : \sin\theta : 1 = x : y : r \]
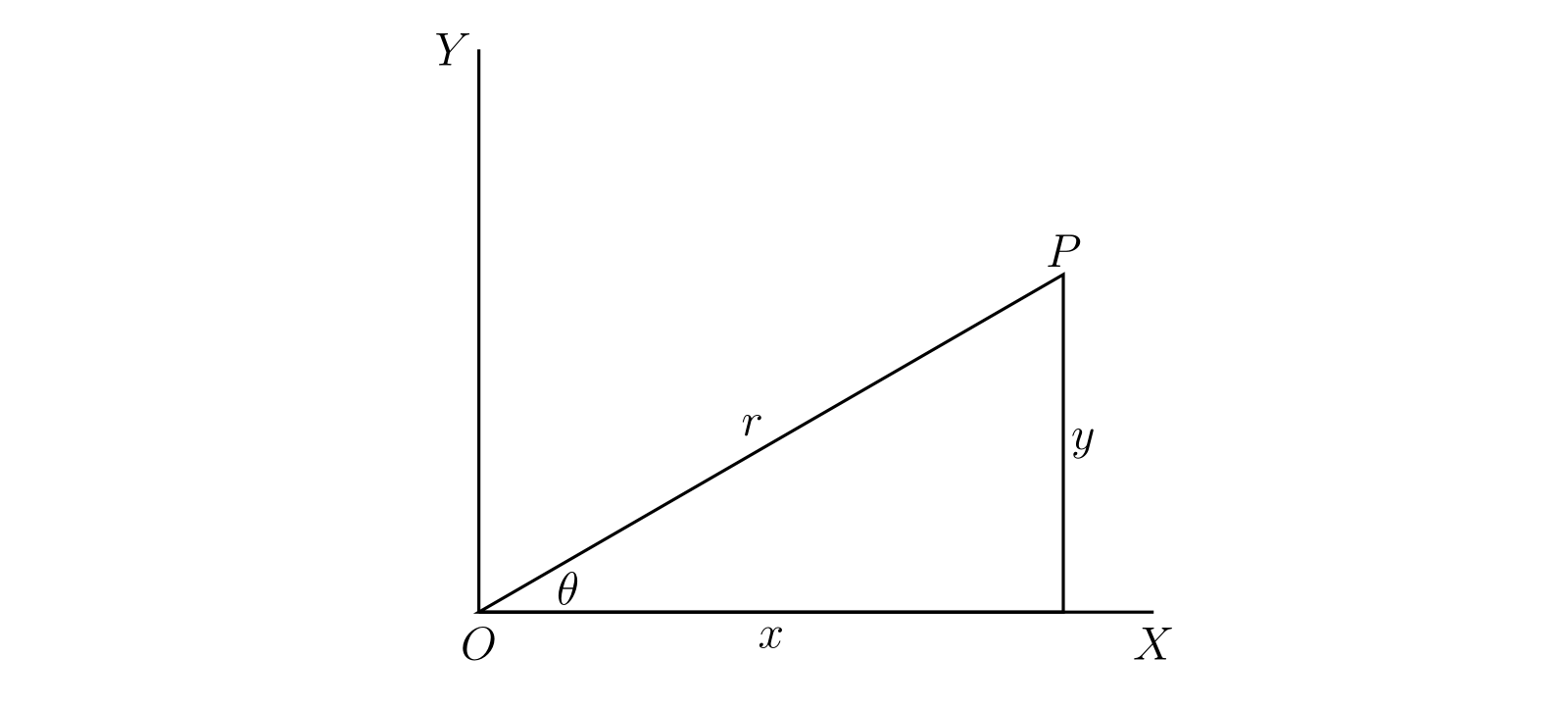
§43 と同様に \(x + yi\) を \(z\) と表記し、\(z\) を複素変数 (complex variable) と呼ぶ。そして \(P\) は点 \(\bm{z}\)、あるいは \(z\) に対応する点と呼び、\(z\) は \(P\) の引数 (argument)、\(x\) は \(z\) の実部 (real part)、\(y\) は \(z\) の虚部 (imaginary part)、\(r\) は \(z\) の大きさ (modulus)、\(\theta\) は \(z\) の 偏角 (argument)7 と呼ぶ。そして次のように表記する: \[ x = \operatorname{Re}(z),\quad y = \operatorname{Im}(z),\quad r = |z|,\quad \theta = \arg z \]
\(y = 0\) のとき \(z\) を実数と呼び、\(x = 0\) のとき \(z\) を純虚数 (pure imaginary number)と呼ぶ。虚部の符号だけが異なる二つの複素数 \(x + yi\) と \(x - yi\) は共役 (conjugate) であると言う。共役な複素数の和 \(2x\) と積 \(x^{2} + y^{2}\) は両方とも実数であり、二つの大きさ \(\sqrt{x^{2} + y^{2}}\) は等しく、大きさは積の二乗に等しい。例えば実数係数二次方程式の二つの根が実数でない場合、それらは共役となる。
\(\theta\) すなわち \(\arg z\) は \(x\) と \(y\) の多値関数であり、\(2\pi\) だけ離れた値を無限に取ることに注意する必要がある8。\(OX\) 上にある直線を原点を中心にこれらの角度だけ回転させると、その直線は \(OP\) に向くようになる。この中で \(-\pi\) から \(\pi\) にある角度を、\(z\) の偏角の主値 (principal value) と呼ぶ。どの値を主値とするかは事前に決めておかなくてはならない。これからは、明示的に示さない限り、「\(z\) の偏角」で \(z\) の偏角の主値を表す。
図 24 をアルガン図 (Argand's diagram) と呼ぶ。
§45 ド・モアブルの定理
次の命題は加算と乗算の定義から直ちに従う:
- 二つの複素数の和の実部 (および和の虚部) は二つの実部の和 (および虚部の和) に等しい。
- 二つの複素数の積の大きさは二つの大きさの積に等しい。
- 二つの複素数の積の偏角は二つの偏角の和に等しいか、二つの偏角の和から \(2\pi\) 離れた値に等しい。
\(\arg(zz')\) の主値が常に \(\arg z\) の主値と \(\arg z'\) の主値の和であるとは限らない。例えば \(z = z' = -1 + i\) とすれば \(z\) と \(z'\) の偏角の主値はどちらも \(\frac{3}{4}\pi\) となる。しかし \(zz' = -2i\) なので \(\arg(zz')\) の主値は \(-\frac{1}{2}\pi\) であり、\(\frac{3}{2}\pi\) ではない。
最後の二つの定理は次の等式として表せる: \[ r(\cos\theta + i\sin\theta) × \rho(\cos\phi + i\sin\phi) = r\rho\{\cos(\theta + \phi) + i\sin(\theta + \phi)\} \] 証明は左辺を計算して \(\cos(\theta + \phi)\) と \(\sin(\theta + \phi)\) に関する三角関数の公式を使えば簡単に行える。さらに一般的に言うと、次が成り立つ: \[ \begin{gathered} r_{1}(\cos\theta_{1} + i\sin\theta_{1}) × r_{2}(\cos\theta_{2} + i\sin\theta_{2}) × \cdots × r_{n}(\cos\theta_{n} + i\sin\theta_{n})\\ = r_{1}r_{2} \cdots r_{n} \{\cos(\theta_{1} + \theta_{2} + \cdots + \theta_{n}) + i \sin(\theta_{1} + \theta_{2} + \cdots + \theta_{n})\} \end{gathered} \]
特に重要なのが \[ r_{1} = r_{2} = \cdots = r_{n} = 1, \quad \theta_{1} = \theta_{2} = \cdots = \theta_{n} = \theta \] とした場合であり、次の式が得られる: \[ (\cos\theta + i\sin\theta)^{n} = \cos n\theta + i\sin n\theta \] ここで \(n\) は正の整数を表す。この結果はド・モアブルの定理 (De Moivre's Theorem) として知られる9。
また \[ z = r(\cos\theta + i\sin\theta) \] であれば \[ \frac{1}{z} = \frac{1}{r}(\cos\theta - i\sin\theta) \] となる。つまり \(z\) の逆数の大きさは \(z\) の大きさの逆数であり、\(z\) の逆数の偏角は \(z\) の偏角の符号を反転させたものである。ここから (2) と (3) に対応する商に関する定理を導ける:
- 二つの複素数の商の大きさは二つの大きさの商に等しい。
- 二つの複素数の商の偏角は二つの偏角の差に等しいか、二つの偏角の差から \(2\pi\) 離れた値に等しい。
また \[ \begin{aligned} (\cos\theta + i\sin\theta)^{-n} & = (\cos\theta - i\sin\theta)^{n}\\ & = \{\cos(-\theta) + i\sin(-\theta)\}^{n}\\ & = \cos(-n\theta) + i\sin(-n\theta) \end{aligned} \] だから、ド・モアブルの定理は正と負の整数 \(\bm{n}\) 全てに対して成立する。
定理 (1)–(5) に次の定理を加える。これも同じく非常に重要である。
- 任意個の複素数の和の大きさは、大きさの和と等しいかそれより小さい。
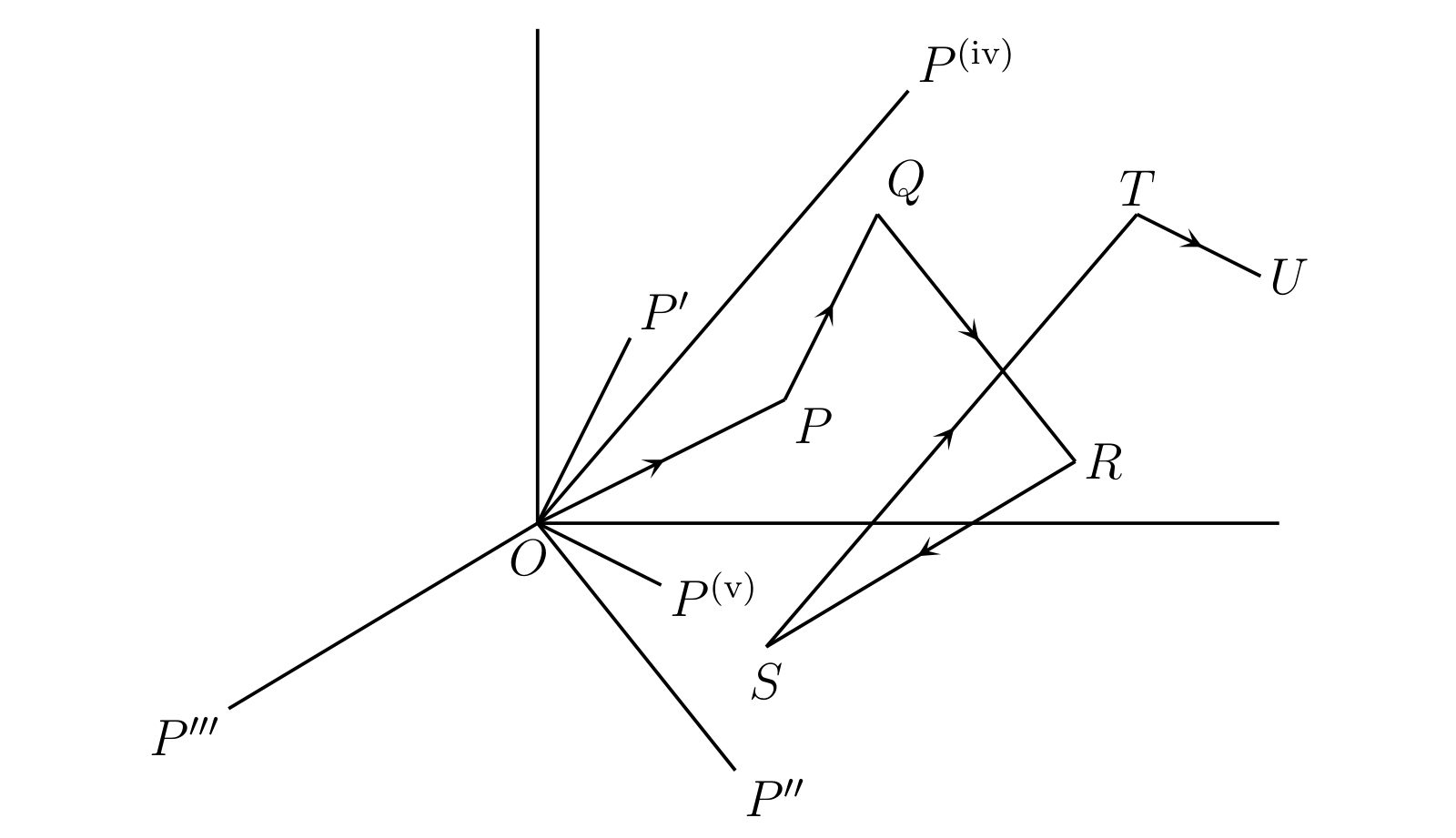
証明は次の通り。\(\overline{OP},\ \overline{OP'},\ \ldots\ \) を複素数に対応する変位とする。\(PQ\) を \(OP'\) と平行で長さが等しいよう取り、\(QR\) を \(OP''\) と平行で長さが等しいように取る。以降も続けて取っていくと、最後の点 \(U\) では次が成り立つ: \[ \overline{OU} = \overline{OP} + \overline{OP'} + \overline{OP''} + \cdots \] \(OU\) の長さは考えている複素数の和の大きさと等しい。一方で複素数の大きさの和は折れ線 \(OPQR \ldots U\) の全長なので、\(OU\) より大きくはならない。
代数だけを使ったこの定理の証明の概略が 例 21.1 にある。
§46 複素変数の有理関数
複素数の有理関数に関する定理をさらにいくつか紹介する。複素変数 \(z\) の有理関数 (rational function) の定義は実変数 \(x\) の有理関数の定義と全く同じであり、二つの \(z\) の多項式の商と定義される。
任意の有理関数 \(R(z)\) は \(x\) と \(y\) の実数係数有理関数 \(X\) と \(Y\) を使って \(X + Yi\) と書ける。
まず加算と乗算の定義から、任意の多項式 \(P(x + yi)\) が \(x\) と \(y\) の実数係数多項式 \(A\) と \(B\) を使って \(A + Bi\) と書けることが分かる。同様に \(Q(x + yi)\) も \(C + Di\) と書ける。よって \[ R(x + yi) = \frac{P(x + yi)}{Q(x + yi)} \] は次のように変形できる: \[ \begin{aligned} \frac{A + Bi}{C + Di} & = \frac{(A + Bi) (C - Di)}{(C + Di) (C - Di)}\\ & = \frac{AC + BD}{C^{2} + D^{2}} + \frac{BC - AD}{C^{2} + D^{2}} i \end{aligned} \] 上述の定理はここから従う。
\(R(z)\) が実数係数の有理関数で、\(R(x + yi) = X + Yi\) が一つ前の定理で示した形のとき、\(R(x - yi) = X - Yi\) が成り立つ。
まず \((x + yi)^{n}\) に対するこの定理は実際に展開すれば容易に得られる。それを足せば実数係数の多項式に対しても成り立つことが分かる。よって一つ前の定理と同じ表記を使えば \[ R(x - yi) = \frac{A - Bi}{C - Di} = \frac{AC + BD}{C^{2} + D^{2}} - \frac{BC - AD}{C^{2} + D^{2}}i \] となる。これは \(i\) の符号が反転している点以外は \(R(x + yi)\) と等しい。この二つの定理は複素変数の数がいくつでも成り立つ。
実数係数の方程式 \[ a_{0}z^{n} + a_{1}z^{n-1} + \cdots + a_{n} = 0 \] の実数でない根は、共役な複素数の組からなる。
\(x + yi\) が根のときは \(x - yi\) も根であることが二番目の定理から分かる。この定理の特殊な場合として、実数係数二次方程式の根が実数または共役な複素数であるという §43 で示した結果が得られる。
この定理は次のように表現されることもある: 実数係数の多項式では、複素根は共役な組として表れる。これを 例 8.7 で示した有理数係数の多項式では、無理根が共役な組として現れるという事実と比較するとよい10。
-
§45 の定理 (6) を定義から直接、幾何学的な手段を使わずに示せ。
[まず \(|z + z'| \leq |z| + |z'|\) を示すために \[ (x + x')^{2} + (y + y')^{2} \leq \left\{\sqrt{x^{2} + y^{2}} + \sqrt{{x'}^{2} + {y'}^{2}}\right\}^{2} \] を示す。一般の場合へは簡単に拡張できる]
-
等式 \[ |z| + |z'| + \cdots = |z + z' + \cdots| \] が成り立つのは \(z,\ z',\ \ldots\ \) が全て同じ偏角を持つ場合に限ることを示せ。幾何学的な証明と解析的な証明の両方を示すこと。
-
任意個の複素数の和の大きさは、その実部 (または虚部) の和より大きくない。
-
二つの複素数の和と積がどちらも実数とする。このとき両方とも実数であるか、そうでなければ共役である。
-
もし \[ a + b\sqrt{2} + (c + d \sqrt{2})i = A + B\sqrt{2} + (C + D\sqrt{2})i \] で \(a,\ b,\ c,\ d,\ A,\ B,\ C,\ D\) が全て有理数の実数なら、以下が成り立つ: \[ a = A,\quad b = B,\quad c = C,\quad d = D \]
-
次の数を実数 \(A,\ B\) を使った \(A + Bi\) という形で表せ: \[ (1 + i)^{2},\quad \left(\frac{1 + i}{1 - i}\right)^{2},\quad \left(\frac{1 - i}{1 + i}\right)^{2},\quad \frac{\lambda + \mu i}{\lambda - \mu i},\quad \left(\frac{\lambda + \mu i}{\lambda - \mu i}\right)^{2} - \left(\frac{\lambda - \mu i}{\lambda + \mu i}\right)^{2} \] \(\lambda\) と \(\mu\) は実数とする。
-
次の \(z = x + yi\) の関数を、\(x\) と \(y\) の実関数 \(X\) と \(Y\) を使って \(X + Yi\) という形で表せ。\(\alpha,\ \beta,\ \gamma,\ \delta\) は実数とする: \[ z^{2},\quad z^{3},\quad z^{n},\quad \frac{1}{z},\quad z + \frac{1}{z},\quad \frac{\alpha + \beta z}{\gamma + \delta z} \]
-
上の二つの例に登場する複素数と関数の大きさを求めよ。
-
\(z = a\) と \(z = b\) および \(z = c\) と \(z = d\) をつないだ二つの直線が直行するのは \[ \arg\left(\frac{a - b}{c - d}\right) = ±\frac{1}{2} \pi \] が成り立つとき、つまり \((a - b)/(c - d)\) が純虚数なときだと示せ。二つの直線が平行になるための条件は何か?
-
三角形の三頂点が複素数 \(\alpha,\ \beta,\ \gamma\) を使って \(z = \alpha,\ z = \beta,\ z = \gamma\) と与えられる。次の命題を示せ:
- 重心は \(z = \frac{1}{3}(\alpha + \beta + \gamma)\) を満たす。
- 外心は \(|z - \alpha| = |z - \beta| = |z - \gamma|\) を満たす。
- 各頂点から反対側の辺に引いた垂線が交わる点は次の式を満たす: \[ \operatorname{Im}\left(\frac{z - \alpha}{\beta - \gamma}\right) = \operatorname{Im}\left(\frac{z - \beta}{\gamma - \alpha}\right) = \operatorname{Im}\left(\frac{z - \gamma}{\alpha - \beta}\right) = 0 \]
- 三角形の内部にある点 \(P\) であって \[ \angle CBP = \angle ACP = \angle BAP = \omega \] および次の式を満たすものが存在する: \[ \cot\omega = \cot A + \cot B + \cot C \]
[(iii) の証明では、\(z\) が表す点を \(P\) としたときに \(AP\) と \(BC\) が垂直となるための条件が「\((z - \alpha)/(\beta - \gamma)\) が純虚数」つまり次の式であることを利用する: \[ \operatorname{Re}(z - \alpha) \operatorname{Re}(\beta - \gamma) + \operatorname{Im}(z - \alpha) \operatorname{Im}(\beta - \gamma) = 0 \] この方程式の \(\alpha,\ \beta,\ \gamma\) を巡回させた三つの方程式は、全て同じ \(z\) によって満たされる。これは三つの左辺の和が \(0\) なことから分かる。
(iv) の証明は次のようにする。\(BC\) を \(x\) 軸正方向と平行に取ると11、次が成り立つ: \[ \gamma - \beta = a,\quad \alpha - \gamma = - b \operatorname{Cis}(-C),\quad \beta - \alpha = - c \operatorname{Cis} B \]
\(z\) と \(\omega\) は次の方程式から求めなければならない: \[ \frac{(z - \alpha)(\beta_{0} - \alpha_{0})} {(z_{0} - \alpha_{0})(\beta - \alpha)} = \frac{(z - \beta)(\gamma_{0} - \beta_{0})} {(z_{0} - \beta_{0})(\gamma - \beta)} = \frac{(z - \gamma)(\alpha_{0} - \gamma_{0})} {(z_{0} - \gamma_{0})(\alpha - \gamma)} = \operatorname{Cis} 2\omega \] ここで \(z_{0},\ \alpha_{0},\ \beta_{0},\ \gamma_{0}\) は \(z,\ \alpha,\ \beta,\ \gamma\) の共役を表す。
三つの式の分母と分子を足して、さらに \[ i\cot\omega = \frac{1 + \operatorname{Cis} 2\omega}{1 - \operatorname{Cis} 2\omega} \] を使えば \[ i\cot\omega = \frac{(\beta - \gamma)(\beta_{0} - \gamma_{0}) + (\gamma - \alpha)(\gamma_{0} - \alpha_{0}) + (\alpha - \beta)(\alpha_{0} - \beta_{0})} {\beta\gamma_{0} - \beta_{0}\gamma + \gamma\alpha_{0} - \gamma_{0}\alpha + \alpha\beta_{0} - \alpha_{0}\beta} \] が分かる。よって \(\Delta\) を三角形の面積とすれば、\(\cot\omega\) の値が \((a^{2} + b^{2} +c^{2})/4\Delta\) だと容易に示せる。これは示したい式と同値である。
\(z\) を求めるには、分数の等式の分母と分子にそれぞれ \((\gamma_{0} - \beta_{0})/(\beta - \alpha),\ (\alpha_{0} - \gamma_{0})/(\gamma - \beta),\ (\beta_{0} - \alpha_{0})/(\alpha - \gamma)\) を乗じる。すると最終的に \[ z = \frac{a\alpha \operatorname{Cis} A + b\beta \operatorname{Cis} B + c\gamma \operatorname{Cis} C} {a\operatorname{Cis} A + b\operatorname{Cis} B + c\operatorname{Cis} C} \] が求まる]
-
複素数 \(a,\ b,\ c\) と \(x,\ y,\ z\) からなる二つの三角形は、次の等式が成り立つとき相似となる: \[ \begin{vmatrix} 1 & 1 & 1\\ a & b & c \\ x & y & z \end{vmatrix} = 0 \]
[必要な条件は \(\overline{AB}/\overline{AC} = \overline{XY}/\overline{XZ}\) (小文字を引数に持つ点を大文字で表す) あるいは \((b - a)/(c - a) = (y - x)/(z - x)\) である]
-
\(x,\ y,\ z\) が一直線上にあるときには \(\alpha + \beta + \gamma = 0\) かつ \(\alpha x + \beta y + \gamma z = 0\) となるように実数 \(\alpha,\ \beta,\ \gamma\) を取れることを前問を使って示せ。またこの逆も示せ (参考: 例 20.4)。 [この設定では \(x,\ y,\ z\) からなる三角形が軸 \(OX\) 上にある潰れた三角形と相似になるので、前問の結果が適用できる]
-
複素係数の一般的な線形方程式: 方程式 \(\alpha z + \beta = 0\) は \(\alpha \neq 0\) なら唯一の解 \(z = -(\beta/\alpha)\) を持つ。もし \[ \alpha = a + Ai,\quad \beta = b + Bi,\quad z = x + yi \] なら、実部と虚数を等号で結ぶことで二つの実数 \(x\) と \(y\) を決定する二つの方程式を得る。\(y = 0\) なら方程式は実根を持ち、\(ax + b = 0,\ Ax + B = 0\) が成り立つ。この連立方程式が矛盾しない解を持つ条件は \(aB - bA = 0\) である。
-
複素係数の一般的な二次方程式は次の形をしている: \[ (a + Ai)z^{2} + 2(b + Bi)z + (c + Ci) = 0 \]
\(a\) と \(A\) が両方ともゼロでないなら \(a + iA\) で両辺を割れるので、 \[ z^{2} + 2(b + Bi)z + (c + Ci) = 0 \qquad \text{(1)} \] が一般的な形となる。\(z = x + yi\) を代入して実部と虚部をそれぞれ等号で結べば、\(x\) と \(y\) に関する連立方程式を得る: \[ x^{2} - y^{2} + 2(bx - By) + c = 0, \quad 2xy + 2(by + Bx) + C = 0 \]
さらに \[ x + b = \xi, \quad y + B = \eta, \quad b^{2} - B^{2} - c = h, \quad 2bB - C = k \] と置けば、次の式が得られる: \[ \xi^{2} - \eta^{2} = h, \quad 2\xi\eta = k \]
二乗して足せば \[ \begin{gathered} \xi^{2} + \eta^{2} = \sqrt{h^{2} + k^{2}}, \\ \xi = ±\sqrt{\tfrac{1}{2}\{\sqrt{h^{2} + k^{2}} + h\}}, \quad \eta = ±\sqrt{\tfrac{1}{2}\{\sqrt{h^{2} + k^{2}} - h\}} \end{gathered} \] を得る。ここで \(\xi\) と \(\eta\) の符号は \(\xi\eta\) の符号が \(k\) と同じになるよう選ぶ。つまり \(k\) が正なら同じ符号を、\(k\) が負なら違う符号を取る。
-
重根の条件: 二つの根が等しいのは「\(h = 0\) かつ \(k = 0\)」すなわち「\(c = b^{2} - B^{2}\) かつ \(C = 2bB\)」が成り立つときに限る。この条件は単一の式 \(c + Ci = (b + Bi)^{2}\) と同値であり、方程式 (1) の左辺が完全平方になることを意味する。
-
実根の条件: \(x^{2} + 2(b + Bi) x + (c + Ci) = 0\) を満たす \(x\) が実数なら、\(x^{2} + 2bx + c = 0\) かつ \(2Bx + C = 0\) となる。\(x\) を削除すればこの条件を単純化できる: \[ C^{2} - 4bBC + 4cB^{2} = 0 \]
-
純虚数根の条件: これは容易に分かる: \[ C^{2} - 4bBC - 4b^{2}c = 0 \]
-
共役な複素根の組の条件: 二つの共役な複素数の和と積はどちらも実数なので、\(b + Bi\) と \(c + Ci\) は両方とも実数である。つまり \(B = 0\) かつ \(C = 0\) でなければならない。よって (1) が共役な複素根を持つのは係数が実数のときに限る。根の明示的な表現を見てもこのことを確認できる。加えてもし \(b^2 \geq c\) ならこの場合でも根は実数となるので、共役な複素根のための条件は「\(B = 0\) かつ \(C = 0\) かつ \(b^{2} \lt c\)」となる。
-
-
三次方程式: \(G,\ H\) を複素数として \[ z^{3} + 3Hz + G = 0 \] を考える。この方程式にあり得るのは (i) 実根 (ii) 純虚根 (iii) 共役な複素根である。\(H = \lambda + \mu i\) および \(G = \rho + \sigma i\) とすれば、次が分かる:
-
実根の条件: \(\mu\) が \(0\) でないなら実根は \(-\sigma/3\mu\) であり、加えて \(\sigma^{3} + 27\lambda\mu^{2}\sigma - 27\mu^{3}\rho = 0\) が成り立つ。一方 \(\mu = 0\) なら \(\sigma = 0\) でもないと方程式の係数が実数とならない。後者の場合には三つの実根が存在する。
-
純虚根の条件: \(\mu\) が \(0\) でないなら純虚根は \((\rho/3\mu)i\) であり、\(\rho^{3} - 27\lambda\mu^{2}\rho - 27\mu^{3}\sigma = 0\) が成り立つ。一方 \(\mu = 0\) なら \(\rho = 0\) であり、純虚根は実数係数を持つ三次方程式 \(y^{3} - 3\lambda y - \sigma = 0\) の解 \(y\) を使って \(yi\) と表せる。後者の場合には三つの純虚根が存在する。
-
共役な複素根の組の条件: 根を \(x + yi,\ x - yi\) とすると、三つの根の和が \(0\) であることから三つ目の根は \(-2x\) となる。多項式の係数と根の関係から \[ y^{2} - 3x^{2} = 3H,\quad 2x(x^{2} + y^{2}) = G \] が分かる。よって \(G\) と \(H\) はどちらも実数でなくてはならない。
いずれの場合でも、実数係数の三次方程式への帰着もしくは根そのものが見つかる (見つかった根で方程式を割れば二次方程式に帰着できる)。
-
- \(a_{1} = A_{1} + A_{1}'i,\ \ldots\) として三次方程式 \(x^{3} + a_{1}x^{2} + a_{2}x + a_{3} = 0\) を考える。この方程式が共役な複素根の組を持つとき、\(A_{3}' \neq 0\) なら最後の根が \(-A_{1}'a_{3}/A_{3}'\) だと示せ。\(A_{3}' = 0\) のケースも調べよ。
-
\(z^{3} + 3Hz + G = 0\) が二つの虚数根を持つなら、方程式 \[ 8\alpha^{3} + 6\alpha H - G = 0 \] は一つの実根を持ち、それは一つ目の方程式の複素根の実部 \(\alpha\) であることを証明せよ。さらに \(\alpha\) の符号が \(G\) と同じことを示せ。
-
複素係数の方程式は、その次数に関わらず一般には実根や共役な複素根を持つとは限らない。方程式が (a) 実根あるいは (b) 共役な複素根の組を持つために係数が満たすべき条件はそれぞれ何か?
-
同軸円: 図 26 で \(A,\ B,\ P\) の引数を \(a,\ b,\ z\) とする。このとき主値を考えれば、 \[ \arg\frac{z - b}{z - a} = \angle APB \] が成り立つ。図中二つの円が等しいとする。\(P',\ P_{1},\ P_{1}'\) の引数が \(z',\ z_{1},\ z_{1}'\) で \(\angle APB = \theta\) なら \[ \arg\frac{z' - b}{z' - a} = \pi - \theta,\quad \arg\frac{z_{1} - b}{z_{1} - a} = -\theta \] および次が成り立つ: \[ \arg\frac{z_{1}' - b}{z_{1}' - a} = -\pi + \theta \]
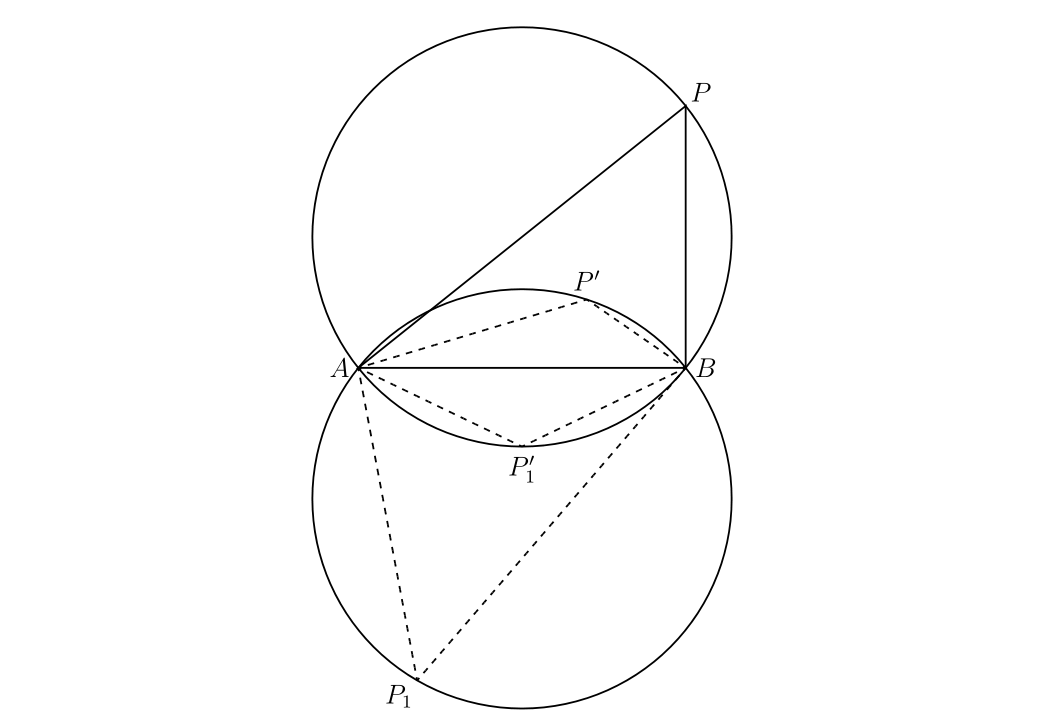 図 26
図 26\(\theta\) を定数とすると、方程式 \[ \arg\frac{z - b}{z - a} = \theta \] で定まる軌跡は弧 \(APB\) である。\(\theta\) の代わりに \(\pi - \theta,\ -\theta,\ -\pi + \theta\) とすれば、他の三つの弧も得られる。
\(\theta\) がパラメータだとする。このとき \(\theta\) を \(-\pi\) から \(\pi\) まで変化させて得られる方程式の系は二点 \(\bm{A,\ B}\) を通る円全体を表す。ここで一つの円は異なる \(\theta\) に対応する二つの部分から構成される。
-
方程式 \[ \left|\frac{z - b}{z - a}\right| = \lambda \qquad \text{(1)} \] を考える。\(\lambda\) は定数とする。
\(P\) を適当な点とし、三点 \(A\, B\, P\) を通る円の \(P\) を通る接線が \(AB\) と交わる点を \(K\) とする。このとき \(\triangle KPA\) と \(\triangle KBP\) は相似だから、次の式が成り立つ: \[ AP/PB = PK/BK = KA/KP = \lambda \] よって \(KA/KB = \lambda^{2}\) であり、方程式 (1) を満たす任意の \(P\) について \(K\) は固定点だと分かる。また \(KP^{2} = KA · KB\) であり、これは定数となる。よって \(\bm{P}\) の軌跡は \(\bm{K}\) を中心とする円である。
\(\lambda\) を変化させたときに得られる方程式の系は円の系を定義し、その円の全てが問題 19 で考えた系に含まれる全ての円と直行する。
問題 19 の系は共通点を持つ同軸円の系 (system of coaxal circles of the common point kind) と呼ばれる。問題 20 の系は 極限点を持つ同軸円の系 (system of coaxal circles of the limiting point kind) と呼ばれ、\(A\) と \(B\) を極原点 (limiting point) と呼ぶ。\(\lambda\) が非常に小さいあるいは非常に大きい場合、極限点 \(A,\ B\) を持つ同軸円は \(A\) または \(B\) を内部に含む非常に小さい円となる。
-
双一次変換: 次の方程式を考える: \[ z = Z + a \qquad \text{(1)} \] ここで \(z = x + yi\) と \(Z = X + Yi\) は複素変数であり、それぞれ平面 \(xoy\) と平面 \(XOY\) という異なる平面上にあるとする。全ての \(z\) の値には一つの \(Z\) の値が対応し、逆も成り立つ。\(a = \alpha + \beta i\) とすれば \[ x = X + \alpha,\quad y = Y + \beta \] であり、\((x, y)\) に \((X, Y)\) が対応する。もし \((x, y)\) が \(xoy\) 平面上のある曲線を表しているなら、\((X, Y)\) は \(XOY\) 平面における何らかの曲線を表す。つまり一方の平面上の任意の図形がもう一方の平面上の何らかの図形に対応する。(1) のような関係を使って平面 \(xoy\) 上の図形を平面 \(XOY\) 上の図形に対応付けるこの変形処理を、変換 (transformation) と呼ぶ。この例では二つの図形の間の関係が非常に簡単に定義されている。具体的に言うと \((X, Y)\) が表す図形は \((x, y)\) が表す図形と同じ大きさ・形・傾きを持ち、\(\alpha\) だけ左に、\(\beta\) だけ下に移動している。このような変換を移動 (translation) と呼ぶ。
次に方程式 \[ z = \rho Z \qquad \text{(2)} \] を考える (\(\rho\) は実数)。このとき \(x = \rho X,\ y = \rho Y\) が成り立つ。二つの図形は相似で、任意の点はそれぞれの原点から見て相似な点に配置される。\((x, y)\) の図形の大きさは \((X, Y)\) の図形の大きさの \(\rho\) 倍となる。こういった変換を拡大 (magnification) と呼ぶ。
最後に方程式 \[ z = (\cos\phi + i \sin\phi)Z \qquad \text{(3)} \] を考える。明らかに \(|z| = |Z|\) であり、\(\arg z\) と \(\arg Z + \phi\) はどこかで等しい。\((x, y)\) の図形と \((X, Y)\) の図形の唯一の違いは図形が原点中心に正方向に \(\phi\) だけ回転している点である。こういった変換を回転 (rotation) と呼ぶ。
一般的な線形変換 \[ z = aZ + b \qquad \text{(4)} \] は変換 (1), (2), (3) を組み合わせたものである。実際 \(|a| = \rho\) および \(\text{am a} = \phi\) とすれば、(4) を次の三つの式で表せる: \[ z = z' + b, \quad z' = \rho Z', \quad Z' = (\cos\phi + i\sin\phi)Z \] つまり一般的な線形変換は、移動・拡大・回転を組み合わせたものと等しい。
続いて次の変換を考える: \[ z = \frac{1}{Z} \qquad \text{(5)} \] \(|Z| = R\) および \(\arg Z = \Theta\) とすれば、\(|z| = 1/R\) と \(\arg z = -\Theta\) が成り立つ。\((x, y)\) の図形から \((X, Y)\) の図形を得るには、まず前者を原点中心に単位円に関して反転させ、次に軸 \(ox\) に関して図を反転させればよい。
最後に変換 \[ z = \frac{aZ + b}{cZ + d} \qquad \text{(6)} \] を考える。これは次の変換を組み合わせたものと等しい: \[ \begin{aligned} z & = (a/c) + (bc - ad)(z'/c), \\ z' & = 1/Z', \\ Z' & = cZ + d \end{aligned} \] 言い換えると、これまでに考えた全ての種類の変換をとある順番で組み合わせたものは式 (6) で表せる。
変換 (6) を一般双一次変換 (general bilinear transformation) と呼ぶ。\(Z\) について解けば次を得る: \[ Z = \frac{dz - b}{cz - a} \]
全ての \(z\) の値がちょうど一つの \(Z\) の値に対応し、さらにその逆も成り立つような変換を考えた場合、一般双一次変換はその中で最も一般的な変換である。
-
一般双一次変換は円を円に変換する: 証明は何種類かある。反転が円を円に (特殊ケースでは直線に) 変換するというよく知られた幾何学の定理を使うこともできるし、問題 19 と問題 20 の結果を使うこともできる。例えば点 \((x, y)\) から構成される円が \[ \left| \frac{z - \sigma}{z - \rho} \right| = \lambda \] なら、\(z\) に \(Z\) を代入すれば \[ \left|\frac{Z - \sigma'}{Z - \rho'} \right| = \lambda' \] を得る。新しい記号は次の通り: \[ \sigma' = -\frac{b - \sigma d}{a - \sigma c}, \quad \rho' = -\frac{b - \rho d}{a - \rho c}, \quad \lambda' = \left|\frac{a - \rho c}{a - \sigma c}\right|\lambda \]
-
変換 \(z = 1/Z,\ z = (1 + Z)/(1 - Z)\) について、(1) 原点中心の円および (2) 原点を通る直線のそれぞれに対応する曲線 \((X, Y)\) を描け。
-
変換 \(z = (aZ + b)/(cZ + d)\) が円 \(x^{2} + y^{2} = 1\) を直線に変換するための条件は \(|a| = |c|\) である。
-
複比 (cross ratio) \((z_{1}, z_{2}; z_{3}, z_{4})\) は次のように定義される: \[ \frac{(z_{1} - z_{3}) (z_{2} - z_{4})}{(z_{1} - z_{4}) (z_{2} - z_{3})} \]
四点 \(z_{1},\ z_{2},\ z_{3},\ z_{4}\) が同じ直線にあるなら、この定義は初等幾何学のものと同様になる。\(z_{1},\ z_{2},\ z_{3},\ z_{4}\) の添え字を入れ替えると \(24\) 個の複比を作れるが、その中には異なる値が \(6\) 個含まれる。複比の一つを \(\lambda\) とすれば、六つの複比は \(\lambda,\ 1 - \lambda,\ 1/\lambda,\ 1/(1 - \lambda,\ ) (\lambda - 1)/\lambda,\ \lambda/(\lambda - 1)\) である。これらの値のどれかが \(-1\) に等しいとき、四点は調和 (harmonic) である、あるいは調和関係にある (harmonically related) と言う。このとき六つの複比は \(-1,\ 2,\ -1,\ \frac{1}{2},\ 2,\ \frac{1}{2}\) となる。
複比のいずれかが実数なら全て実数であり、そのとき四点は同一円周上にある。なぜならこのとき \[ \arg\frac{(z_{1} - z_{3}) (z_{2} - z_{4})}{(z_{1} - z_{4}) (z_{2} - z_{3})} \] が \(-\pi,\ 0,\ \pi\) のいずれかであり、\(\arg\{(z_{1} - z_{3})/(z_{1} - z_{4})\}\) と \(\arg\{(z_{2} - z_{3})/(z_{2} - z_{4})\}\) は等しいか \(\pi\) だけ離れた値になるためである (参考: 問題 19)。
もし \({(z_{1}, z_{2}; z_{3}, z_{4})} = - 1\) なら、二つの条件 \[ \arg\frac{z_{1} - z_{3}}{z_{1} - z_{4}} = ±\pi + \arg\frac{z_{2} - z_{3}}{z_{2} - z_{4}},\quad \left|\frac{z_{1} - z_{3}}{z_{1} - z_{4}}\right| = \left|\frac{z_{2} - z_{3}}{z_{2} - z_{4}}\right| \] が満たされる。つまり四点 \(A_{1},\ A_{2},\ A_{3},\ A_{4}\) は同一円周上に存在し、\(A_{1}\) と \(A_{2}\) の間に \(A_{3}\) と \(A_{4}\) がある。さらに \(A_{1}A_{3}/A_{1}A_{4} = A_{2}A_{3}/A_{2}A_{4}\) が成り立つ: \(A_{3}A_{4}\) の中点を \(O\) とする。仮定の式 \[ \frac{(z_{1} - z_{3}) (z_{2} - z_{4})}{(z_{1} - z_{4}) (z_{2} - z_{3})} = -1 \] を変形すると \[ (z_{1} + z_{2}) (z_{3} + z_{4}) = 2(z_{1}z_{2} + z_{3}z_{4}) \] となり、さらに \[ \{z_{1} - \frac{1}{2}(z_{3} + z_{4})\} \{z_{2} - \frac{1}{2}(z_{3} + z_{4})\} = \{\frac{1}{2}(z_{3} - z_{4})\}^{2} \] とも書ける。これは \(\overline{OA_{1}} · \overline{OA_{2}} = \overline{OA_{3}}^{2} = \overline{OA_{4}}^{2}\) と同値である。よって \(OA_{1}\) が \(A_{3}A_{4}\) となす角度は \(OA_{2}\) が \(A_{3}A_{4}\) となす角度と等しく、さらに \(OA_{1} · OA_{2} = OA_{3}^{2} = OA_{4}^{2}\) と分かる。この議論における \(A_{1}, A_{2}\) と \(A_{3}, A_{4}\) の対称性に注目すれば、\(A_{1}A_{2}\) の中点 \(O'\) について \(O'A_{3}\) と \(A_{1}A_{2}\) がなす角度と \(O'A_{4}\) と \(A_{1}A_{2}\) がなす角度も等しく、さらに \(O'A_{3} · O'A_{4} = O'A_{1}^{2} = O'A_{2}^{2}\) も成り立つことが分かる。
-
点 \(A_{1},\ A_{2}\) が \(az^{2} + 2bz + c = 0\) で与えられ、点 \(A_{3},\ A_{4}\) が \(a'z^{2} + 2b'z + c' = 0\) で与えられ、\(A_{3}A_{4}\) の中点が \(O\) であり、\(ac' + a'c - 2bb' = 0\) とする。このとき \(OA_{1}\) と \(OA_{2}\) が \(A_{3}A_{4}\) となす角度は等しく、\(OA_{1} · OA_{2} = OA_{3}^{2} = OA_{4}^{2}\) が成り立つ。
(Math. Trip. 1901.)
-
アルガン図において \(AB,\ CD\) を交点を持つ二つの線分とし、\(P,\ Q\) をそれらの中点とする。もし \(AB\) が \(\angle CPD\) を二等分して \(PA^{2} = PB^{2} = PC · PD\) なら、\(CD\) は \(\angle AQB\) を二等分して \(QC^{2} = QD^{2} = QA · QB\) なことを示せ
(Math. Trip. 1909.)
-
四点が円周上にある条件: 十分条件は複比のどれか (結局は全て) が実数なこと (問題 25) だが、この条件は必要でもある。別の表現を使うと、この条件は「次の式が成り立つように実数 \(\alpha,\ \beta,\ \gamma\) を選べること」となる: \[ \begin{vmatrix} 1 & 1 & 1\\ \alpha & \beta & \gamma\\ z_{1}z_{4} + z_{2}z_{3} & z_{2}z_{4} + z_{3}z_{1} & z_{3}z_{4} + z_{1}z_{2} \end{vmatrix} = 0 \] [証明には、変換 \(Z = 1/(z - z_{4})\) が点 \(z_{4}\) に関する反転処理に等しいことを使う (問題 21)。\(z_{1},\ z_{2},\ z_{3}\) が \(z_{4}\) を通る円周上にあるなら、変換先の点 \(Z_{1} = 1/(z_{1} - z_{4}),\ Z_{2} = 1/(z_{2} - z_{4}),\ Z_{3} = 1/(z_{3} - z_{4})\) は一直線上にある。よって (問題 12 から) 実数 \(\alpha',\ \beta',\ \gamma'\) であって \(\alpha' + \beta' + \gamma' = 0\) かつ \(\alpha'/(z_{1} - z_{4}) + \beta'/(z_{2} - z_{4}) + \gamma'/(z_{3} - z_{4}) = 0\) を満たすものが取れる。これが示したい式と同値なことは簡単に示せる]
-
ド・モアブルの定理と似た実数に対する次の命題を示せ: \(\phi_{1},\ \phi_{2},\ \phi_{3},\ \ldots\ \) が正の鋭角であり \[ \tan\phi_{m+1} = \tan\phi_{m} \sec\phi_{1} + \sec\phi_{m} \tan\phi_{1} \] を満たすなら、次の三つの式が成り立つ: \[ \tan\phi_{m+n} = \tan\phi_{m} \sec\phi_{n} + \sec\phi_{m} \tan\phi_{n}, \] \[ \sec\phi_{m+n} = \sec\phi_{m} \sec\phi_{n} + \tan\phi_{m} \tan\phi_{n} \] \[ \tan\phi_{m} + \sec\phi_{m} = (\tan\phi_{1} + \sec\phi_{1})^{m} \] [数学的帰納法を使う]
-
変換 \(\bm{z = Z^{m}}\): この変換では \(r = R^{m}\) であり、\(\theta\) は \(m\Theta\) から \(2\pi\) の整数倍だけ離れている。\(Z\) が単位円を一周する運動を表すなら、\(z\) は単位円を \(m\) 回周る運動を表す。
このとき \((X, Y)\) 平面を原点を中心に \(2\pi/m\) の角度で \(m\) 個に分割したものそれぞれに \((x, y)\) 平面全体が対応する。逆に \((x, y)\) 平面の各点には \((X, Y)\) 平面の \(m\) 点が対応する。
-
実数の複素関数: \(f(t)\) と \(\phi(t)\) を実変数 \(t\) のとある区間に対して定義された二つの実関数とする。このとき \[ z = f(t) + i\phi(t) \qquad \text{(1)} \] を \(t\) の複素関数 (complex function) と呼ぶ。この関数は次のようにすると曲線として幾何学的に表せる: \[ x = f(t),\quad y = \phi(t) \] この方程式から \(t\) を削除すれば曲線の方程式が得られる。\(z\) が \(t\) の多項式あるいは有理関数で係数が複素数なら、(1) の形に変形することで関数の表す曲線を求められる。
-
\(a\) と \(b\) が複素数で \[ z = a + (b - a)t \] とする。\(a = \alpha + \alpha' i,\ b = \beta + \beta' i\) なら \[ x = \alpha + (\beta - \alpha)t, \quad y = \alpha' + (\beta' - \alpha')t \] となる。関数が表す曲線は \(z = a\) と \(z = b\) を結ぶ直線である。二つの点の間の線分は \(0\) から \(1\) の \(t\) の値の区間に対応する。他の二つの半直線に対応する \(t\) の値を求めよ。
-
もし \[ z = c + \rho\left(\frac{1 + ti}{1 - ti}\right) \] で \(\rho\) が正なら、この関数が表すのは \(c\) を中心とした半径 \(\rho\) の円である。\(t\) が実数全体を動くと、\(z\) は円を一度だけ回る。
-
\(z = (a + bt)/(c + dt)\) という一般的な方程式は円を表す。\(x\) と \(y\) を代入して \(t\) を削除すれば示せるが、これは面倒である。問題 22 の結果を使えばより簡単に示せる: \(z = (a + bZ)/(c + dZ),\ Z = t\) とすれば、実数 \(t\) が動くと \(Z\) は \(X\) 軸上を動く。これは直線だから、\(z\) は円となる。
-
方程式 \[ z = a + 2bt + ct^{2} \] は一般に放物線を表す。\(b/c\) が実数なら直線となる。
-
\(\alpha,\ \beta,\ \gamma\) が実数なら、\(z = (a + 2bt + ct^{2})/(\alpha + 2\beta t + \gamma t^{2})\) は円錐曲線を表す。
[次の式から \(t\) を削除すればよい: \[ \begin{aligned} x & = (A + 2Bt + Ct^{2})/(\alpha + 2\beta t + \gamma t^{2}), \\ y & = (A' + 2B't + C't^{2})/(\alpha + 2\beta t + \gamma t^{2}) \end{aligned} \] ただし \(A + A'i = a,\ B + B'i = b,\ C + C'i = c\) である]
-
§47 複素数の根号
複素数 \(a\) と整数 \(m,\ n\) に対する \(\sqrt[n]{a}\) や \(a^{m/n}\) の意味を今まで定義してこなかった。初等代数における実数 \(a\) に対する根号の定義と同じもの採用するのが自然である。そこで整数 \(n\) に対する \(\sqrt[n]{a}\) および \(a^{1/n}\) を \(z^{n} = a\) を満たす複素数 \(z\) として定義し、整数 \(n,\ m\) に対する \(a^{m/n}\) を \((a^{1/n})^{m}\) として定義する。ただしこの定義からは、方程式の根がいくつ存在するのか、あるいはそもそも存在するのかは明らかでない。
§48 \(z^{n} = a\) の解
正の実数 \(\rho\) と \(-\pi \lt \phi \leq \pi\) を満たす \(\phi\) について \[ a = \rho(\cos\phi + i\sin\phi) \] とする。\(z = r(\cos\theta + i\sin\theta)\) とおけば、前節の方程式は \[ r^{n}(\cos n\theta + i\sin n\theta) = \rho(\cos\phi + i \sin\phi) \] となり、次の関係が成り立つ: \[ r^{n} = \rho,\quad \cos n\theta = \cos\phi,\quad \sin n\theta = \sin\phi \qquad \text{(1)} \]
\(r\) として可能なのは通常の \(\rho\) の \(n\) 乗根 \(\sqrt[n]{\rho}\) のみである。そして後ろの二つの関係が満たされるには、整数 \(k\) に対して \(n\theta = \phi + 2k\pi\) すなわち \[ \theta = \frac{\phi + 2k\pi}{n} \] が必要となる。整数 \(p,\ q\ \) (\(0 \leq q \lt n\)) を使って \(k = pn + q\) とすれば \(\theta = 2p\pi + (\phi + 2q\pi)/n\) であり、\(p\) の値は重要でない。つまり方程式 \[ \bm{z^{n} = a = \rho(\cos\phi + i\sin\phi)} \] はちょうど \(\bm{n}\) 個の解 \(\bm{z = r(\cos\theta + i\sin\theta)}\) を持つ。ここで \(r\) と \(\theta\) は次の関係を満たす: \[ r = \sqrt[n]{\rho},\quad \theta = \frac{\phi + 2q\pi}{n}\quad (q = 0,\ 1,\ 2,\ \ldots,\ n - 1) \]
この \(n\) 個の根が本当に異なる点であることはアルガン図に点をプロットすればすぐに分かる。根の一つ \[ \sqrt[n]{\rho}\{\cos(\phi/n) + i\sin(\phi/n)\} \] を \(\sqrt[n]{a}\) の主値 (principal value) と呼ぶ。
\(a = 1,\ \rho = 1,\ \phi = 0\) である場合が特に興味深い。方程式 \(x^{n} = 1\) の \(n\) 個の根は \[ \cos(2q\pi/n) + i\sin(2q\pi/n)\quad (q = 0,\ 1,\ \ldots,\ n - 1) \] である。これらの複素数を \(1\) の \(n\) 乗根と呼ぶ。主値は \(1\) となる。\(\cos(2\pi/n) + i\sin(2\pi/n)\) を \(\omega_{n}\) と書けば、\(1\) の \(n\) 乗根は次のように表せる: \[ 1,\quad \omega_{n},\quad \omega_{n}^{2},\ \ldots,\quad \omega_{n}^{n-1} \]
-
\(1\) の二乗根は \(1\) と \(-1\) の二つであり、\(1\) の三乗根は \(1,\ \frac{1}{2}(-1 + i\sqrt{3}),\ \frac{1}{2}(-1 - i\sqrt{3})\) の三つ、\(1\) の四乗根は \(1,\ i,\ -1,\ -i\) の四つ、五乗根は次の五つである: \[ \begin{aligned} 1,\quad & & \frac{1}{4} \left[\hphantom{-} \sqrt{5} - 1 + i\sqrt{10 + 2\sqrt{5}}\right],\quad \frac{1}{4} \left[-\sqrt{5} - 1 + i\sqrt{10 - 2\sqrt{5}}\right],\\ & & \frac{1}{4} \left[-\sqrt{5} - 1 - i\sqrt{10 - 2\sqrt{5}}\right],\quad \frac{1}{4} \left[\hphantom{-} \sqrt{5} - 1 - i\sqrt{10 + 2\sqrt{5}}\right]\hphantom{.} \end{aligned} \]
-
次を示せ: \[ 1 + \omega_{n} + \omega_{n}^{2} + \cdots + \omega_{n}^{n-1} = 0 \]
-
次を示せ: \[ (x + y\omega_{3} + z\omega_{3}^{2}) (x + y\omega_{3}^{2} + z\omega_{3}) = x^{2} + y^{2} + z^{2} - yz - zx - xy \]
-
\(a\) の \(n\) 乗根は主値 \(\sqrt[n]{a}\) の積として表せる。
-
例 21.14 から、 \[ z^{2} = \alpha + \beta i \] の根が \[ ± \sqrt{\tfrac{1}{2} \{\sqrt{\alpha^{2} + \beta^{2}} + \alpha\}} ± i\sqrt{\tfrac{1}{2} \{\sqrt{\alpha^{2} + \beta^{2}} - \alpha\}} \] だと分かる。符号が同じか異なるかは \(\beta\) の正負によって決まる。これが §48 の結果と矛盾しないことを示せ。
-
\(\dfrac{x^{2m} - a^{2m}}{x^{2} - a^{2}}\) が次式と等しいことを示せ: \[ \Bigl(x^{2} - 2ax\cos\frac{\pi}{m} + a^{2}\Bigr) \Bigl(x^{2} - 2ax\cos\frac{2\pi}{m} + a^{2}\Bigr) \cdots \Bigl(x^{2} - 2ax\cos\frac{(m - 1)\pi}{m} + a^{2}\Bigr) \] [\(x^{2m} - a^{2m}\) の因数は \[ (x - a),\quad (x - a\omega_{2m}),\quad (x - a\omega_{2m}^{2}),\ \ldots, \quad (x - a\omega_{2m}^{2m-1}) \] である。因数 \(x - a\omega_{2m}^{m}\) は \(x + a\) と等しく、\((x - a\omega_{2m}^{s})\) と \((x - a\omega_{2m}^{2m-s})\) の積が因数 \(x^{2} - 2ax \cos(s\pi/m) + a^{2}\) となる]
-
\(x^{2m+1} - a^{2m+1},\ x^{2m} + a^{2m},\ \) \(x^{2m+1} + a^{2m+1}\) を前問と同じ方法で因数分解せよ。
-
\(x^{2n} - 2x^{n}a^{n} \cos\theta + a^{2n}\) が次式と等しいことを示せ: \[ \begin{aligned} \left(x^{2} - 2xa\cos\frac{\theta}{n} + a^{2}\right) & \left(x^{2} - 2xa\cos\frac{\theta + 2\pi}{n} + a^{2}\right) \cdots \\ & \cdots \left(x^{2} - 2xa\cos\frac{\theta + 2(n - 1)\pi}{n} + a^{2}\right) \end{aligned} \] [等式 \[ x^{2n} - 2x^{n}a^{n} \cos\theta + a^{2n} = \{x^{n} - a^{n}(\cos\theta + i\sin\theta)\} \{x^{n} - a^{n}(\cos\theta - i\sin\theta)\} \] を使い、右辺の二つの式をそれぞれ \(n\) 個の因数に分解する]
-
\(x^{6} - 2x^{3} + 2 = 0\) の根を全て求めよ。
(Math. Trip. 1910.)
-
\(\omega_{n}\) の正確な値を \(\omega_{3} = \frac{1}{2}(-1 + i\sqrt{3})\) のように二乗根だけを使った数値的な形で得る問題は、ユークリッドの構成を使って単位円の中に正 \(n\) 角形を作図する幾何学の問題の代数版と言える。この作図が可能なのは \(\cos(2\pi/n)\) と \(\sin(2\pi/n)\) の長さが作図できるときであり、これは (第二章に関連する例 22 で示したように) 数字が二乗根だけを使って表せるときに限って可能になる。
ユークリッドは \(n = 3,\ 4,\ 5,\ 6,\ 8,\ 10,\ 12,\ 15\) に対する作図を示した。これらの数に \(2\) のべきを乗じた値についても同じ方法を使って作図できる。これ以外にも正多角形の作図が可能な値は存在し、その中で最も興味深いのは \(n = 17\) である。
§49 ド・モアブルの定理の一般形
前節の結果から、\(1\) より大きい正の整数 \(q\) に対する \((\cos\theta + i\sin\theta)^{1/q}\) の一つが \[ \cos(\theta/q) + i\sin(\theta/q) \] だと分かる。正負を問わない整数を \(p\) として両辺を \(p\) 乗すると、\((\cos\theta + i\sin\theta)^{p/q}\) の一つが \(\cos(p\theta/q) + i\sin(p\theta/q)\) となるという定理が得られる。つまり \(\bm{1}\) より大きい任意の有理数 \(\bm{\alpha}\) について、\(\bm{(\cos\theta + i\sin\theta)^{\alpha}}\) の一つは \[ \bm{\cos\alpha\theta + i\sin\alpha\theta} \] に等しい。 これはド・モアブルの定理 (§45) を一般化したものである。
第三章に関するその他の例
-
三角形 \(xyz\) が正三角形となる条件は次の等式で表せる: \[ x^{2} + y^{2} + z^{2} - yz - zx - xy = 0 \] [\(XYZ\) を正三角形とする。変位 \(\overline{ZX}\) と \(\overline{YZ}\) は正または負の方向に \(\frac{2}{3}\pi\) の角度をなす。\(\operatorname{Cis}\frac{2}{3}\pi = \omega_{3}\) より \(\operatorname{Cis}(-\frac{2}{3}\pi) = 1/\omega_{3} = \omega_{3}^{2}\) なので、\(x - z = (z - y)\omega_{3}\) または \(x - z = (z - y)\omega_{3}^{2}\) が成り立つ。したがって \(x + y\omega_{3} + z\omega_{3}^{2} = 0\) または \(x + y\omega_{3}^{2} + z\omega_{3} = 0\) であり、例 22.3 より示すべき結果が得られる]
-
\(XYZ,\ X'Y'Z'\) が三角形で \[ \overline{YZ} · \overline{Y'Z'} = \overline{ZX} · \overline{Z'X'} = \overline{XY} · \overline{X'Y'} \] が成り立つなら、両方とも正三角形である。[仮定から \[ (y - z)(y' - z') = (z - x)(z' - x') = (x - y)(x' - y') = \kappa^{2} \] が分かるので、\(\sum 1/(y' - z') = 0\) すなわち \(\sum {x'}^{2} - \sum y'z' = 0\) を得る。前問を使えば示すべき式が得られる]
-
相似な三角形 \(BCX,\ CAY,\ ABZ\) が三角形 \(ABC\) に隣接しているなら、\(ABC\) と \(XYZ\) の重心が一致することを示せ。
[仮定から \((x - c)/(b - c) = (y - a)/(c - a) = (z - b)/(a - b) = \lambda\) となる。\(\frac{1}{3}(x + y + z)\) を \(a,\ b,\ c\) を使って表す]
-
三角形 \(ABC\) の辺上に \(X,\ Y,\ Z\) を \[ BX/XC = CY/YA = AZ/ZB = r \] となるように取る。三角形 \(ABC\) と \(XYZ\) が相似なら、「両方の三角形が相似である」または「\(r = 1\)」が成り立つ。
-
\(A,\ B,\ C,\ D\) を平面上の点とする。このとき次の不等式が成り立つ: \[ AD · BC \leq BD · CA + CD · AB \] [\(A,\ B,\ C,\ D\) に対応する複素数を \(z_{1},\ z_{2},\ z_{3},\ z_{4}\) とする。等式 \[ (x_{1} - x_{4})(x_{2} - x_{3}) + (x_{2} - x_{4})(x_{3} - x_{1}) + (x_{3} - x_{4})(x_{1} - x_{2}) = 0 \] から、次が成り立つ: \[ \begin{aligned} |(x_{1} - x_{4})(x_{2} - x_{3})| & = |(x_{2} - x_{4})(x_{3} - x_{1}) + (x_{3} - x_{4})(x_{1} - x_{2})|\\ & \leq |(x_{2} - x_{4})(x_{3} - x_{1})| + |(x_{3} - x_{4})(x_{1} - x_{2})|] \end{aligned} \]
-
頂点が同一円周上にある四角形に関するプトレマイオスの定理を、共円な四点の複比が実数であることから導け。 [前問と同じ等式を使う]
-
\(z^{2} + z'^{2} = 1\) のとき \(z,\ z'\) はとある楕円の軸の両端点を表す。さらにその楕円の焦点は点 \(1\) と点 \(-1\) である。 [楕円の半軸を \(CP,\ CD\)、焦点を \(S,\ H\) とする。このとき \(CD\) は \(\angle SPH\) の外角の二等分線と平行であり、さらに \(SP · HP = CD^{2}\) が成り立つ]
-
\(|a + b|^{2} + |a - b|^{2} = 2\{|a|^{2} + |b|^{2}\}\) を示せ。 [これは「\(PQ\) の中点 \(M\)について \(OP^{2} + OQ^{2} = 2OM^{2} + 2MP^{2}\)」という幾何学の命題を解析学の言葉で表したものである]
-
問題 8 を使って次の式を示せ: \[ | a + \sqrt{a^{2} - b^{2}} | + | a - \sqrt{a^{2} - b^{2}} | = | a + b | + | a - b | \] [\(a + \sqrt{a^{2} - b^{2}} = z_{1},\ a - \sqrt{a^{2} - b^{2}} = z_{2}\) とすれば \[ |z_{1}|^{2} + |z_{2}|^{2} = \tfrac{1}{2}|z_{1} + z_{2}|^{2} + \tfrac{1}{2}|z_{1} - z_{2}|^{2} = 2|a|^{2} + 2|a^{2} - b^{2}| \] および \[ (|z_{1}| + |z_{2}|)^{2} = 2\{|a|^{2} + |a^{2} - b^{2}| + |b|^{2}\} = |a + b|^{2} + |a - b|^{2} + 2|a^{2} - b^{2}| \] が成り立つ。こう言い換えることもできる: \(z_{1}\) と \(z_{2}\) を \(\alpha z^{2} + 2\beta z + \gamma = 0\) の根とすれば \[ |z_{1}| + |z_{2}| = \frac{1}{|\alpha|} \{(|-\beta + {\sqrt{\alpha\gamma}}|) + (|-\beta - {\sqrt{\alpha\gamma}}|)\} \] が成り立つ]
-
方程式 \(z^{2} + az + b = 0\) の二つの根がどちらも大きさ \(1\) となる必要十分条件が \[ |a| \leq 2,\quad |b| = 1,\quad \arg b = 2\arg a \] であることを示せ。
[偏角が主値である必要はない]
-
実数係数の方程式 \(x^{4} + 4a_{1}x^{3} + 6a_{2}x^{2} + 4a_{3}x + a_{4} = 0\) が二つの実根と二つの虚数根を持ち、それらが全て同一円周上にあるとする。このとき \[ a_{3}^{2} + a_{1}^{2}a_{4} + a_{2}^{3} - a_{2}a_{4} - 2a_{1}a_{2}a_{3} = 0 \] を示せ。
-
次の条件が成り立つなら、\(a_{0}x^{4} + 4a_{1}x^{3} + 6a_{2}x^{2} + 4a_{3}x + a_{4} = 0\) の四つの根は調和関係にある: \[ a_{0}a_{3}^{2} + a_{1}^{2}a_{4} + a_{2}^{3} - a_{0}a_{2}a_{4} - 2a_{1}a_{2}a_{3} = 0 \] [\(z_{1},\ z_{2},\ z_{3},\ z_{4}\) を方程式の根とする。\(Z_{ab, cd} = (z_{c} - z_{a}) (z_{b} - z_{d}) + {}(z_{c} -z_{b}) (z_{a} - z_{d})\) として、\(Z_{23, 14} Z_{31, 24} Z_{12, 34}\) を係数を使って表す。]
-
直線と虚数点: \(ax + by + c = 0\) を複素係数の方程式とする (もちろん特殊ケースとして実係数でもよい)。
\(x\) に具体的な実数または複素数の値を与えれば、対応する \(y\) の値が得られる。方程式を満たす複素数 \(x\) と \(y\) の組の集まりを虚直線 (imaginary straight line) と呼び、\(x\) と \(y\) の組を虚点 (imaginary point) と呼ぶ。\(x\) と \(y\) は点 \((x, y)\) の座標 (coordinate) である。\(x\) と \(y\) が実数の点を実点 (real point) と呼び、\(a,\ b,\ c\) が全て実数の (または共通因数で割るとそうなる) 直線を実直線と呼ぶ。\(x = \alpha + \beta i,\ y = \gamma + \delta i\) と \(x = \alpha - \beta i,\ y = \gamma - \delta i\) の二点、および次の二つの虚直線を共役 (conjugate) であると言う: \[ \begin{aligned} (A + A'i)x + (B + B'i)y + C + C'i & = 0, \\ (A - A'i)x + (B - B'i)y + C - C'i & = 0 \end{aligned} \]
任意の実直線は無限に多くの共役な虚点の組を持つこと、一般の虚直線はただ一つの実点を持つこと、虚直線は共役な虚点の組を含まないことを示せ。さらに \(\text{(a)}\) 二つの虚点を結ぶ直線が実直線となる条件、および \(\text{(b)}\) 二つの虚直線の交点が実点となる条件をそれぞれ求めよ。
-
次の等式を示せ: \[ \begin{gathered} (x + y + z) (x + y\omega_{3} + z\omega_{3}^{2}) (x + y\omega_{3}^{2} + z\omega_{3}) = x^{3} + y^{3} + z^{3} - 3xyz,\\ (x + y + z) (x + y\omega_{5} + z\omega_{5}^{4}) (x + y\omega_{5}^{2} + z\omega_{5}^{3}) (x + y\omega_{5}^{3} + z\omega_{5}^{2}) (x + y\omega_{5}^{4} + z\omega_{5})\\ = x^{5} + y^{5} + z^{5} - 5x^{3}yz + 5xy^{2}z^{2} \end{gathered} \]
-
次の方程式を解け: \[ x^{3} - 3ax + (a^{3} + 1) = 0, \] \[ x^{5} - 5ax^{3} + 5a^{2}x + (a^{5} + 1) = 0 \]
-
\(f(x) = a_{0} + a_{1}x + \cdots + a_{k}x^{k}\) のとき \[ \frac{f(x) + f(\omega x) + \cdots + f(\omega^{n-1}x)}{n} = a_{0} + a_{n}x^{n} + a_{2n}x^{2n} + \cdots + a_{\lambda n}x^{\lambda n} \] が成り立つ。ここで \(\omega\) は \(x^{n} = 1\) の任意の (\(1\) でない) 根であり、\(\lambda n\) は \(k\) より小さい最大の \(n\) の倍数を表す。\(a_{\mu} + a_{\mu+n}x^{n} + a_{\mu+2n}x^{2n} + \cdots\) に対する同様の公式を示せ。
-
もし \[ (1 + x)^{n} = p_{0} + p_{1}x + p_{2}x^{2} + \cdots \] で \(n\) が正の整数なら、次が成り立つ: \[ \begin{aligned} p_{0} - p_{2} + p_{4} - \cdots & = 2^{\frac{1}{2} n} \cos\frac{1}{4}n\pi, \\ p_{1} - p_{3} + p_{5} - \cdots & = 2^{\frac{1}{2} n} \sin\frac{1}{4}n\pi \end{aligned} \]
-
次の級数の和を求めよ: \[ \frac{x}{2! (n - 2)} + \frac{x^{2}}{5! (n - 5)!} + \frac{x^{3}}{8! (n - 8)!} + \cdots + \frac{x^{n/3}}{(n - 1)!} \] \(n\) は \(3\) の倍数とする。
(Math. Trip. 1899.)
-
複素数 \(t\) が \(|t| = 1\) を満たしながら変化するとき、\(x = (at + b)/(t - c)\) は直線上を動く。ただし \(|c| = 1\) の場合は除く。
-
前問と同じ制約の下で \(t\) が動くとき、\(x = \frac{1}{2}\{at + (b/t)\}\) は一般に楕円を表す。その焦点は \(x^{2} = ab\) で与えられ、軸は \(|a| + |b|\) と \(|a| - |b|\) である。ただし \(|a| = |b|\) のとき \(x\) は二点 \(-\sqrt{ab}\) と \(\sqrt{ab}\) を結んだ線分を表す。
-
\(t\) が実数で \(z = t^{2} - 1 + \sqrt{t^{4} - t^{2}}\) なら、\(t^{2} \lt 1\) のとき \(z\) は \(x^{2} + y^{2} + x = 0\) で表される円上にある。\(t^{2} \gt 1\) では \(\sqrt{t^{4} - t^{2}}\) が \(t^{4} - t^{2}\) の正の平方根を表すとして、\(t\) が大きな正の整数から大きな負の数に変化するときの \(z\) の動きを議論せよ。
(Math. Trip. 1912.)
-
変換 \(z = (aZ + b)/(cZ + d)\) の係数が \(ad - bc = 1\) を満たすとする。\(c \neq 0\) なら、変換には二つの固定点 (fixed point)、つまり変換の前後で変化しない点 \(\alpha\) と \(\beta\) が存在することを示せ。ただし \((a + d)^{2} = 4\) のときには固定点は \(\alpha\) の一つだけとなる。さらに固定点が存在するこの二つのケースにおける変換がそれぞれ次の形で表せることを示せ: \[ \frac{z - \alpha}{z - \beta} = K\frac{Z - \alpha}{Z - \beta},\quad \frac{1}{z - \alpha} = \frac{1}{Z - \alpha} + K \]
そうでなくて \(c = 0\) なら、\(a = b\) でない限り固定点 \(\alpha\) が存在する。こちらの二つのケースは次のように表せる: \[ z - \alpha = K(Z - \alpha),\quad z = Z + K \]
最後に \(a,\ b,\ c,\ d\) が全て正の整数 (\(0\) 含む) という制限が加わったとする。このとき固定点が二つより少ない変換は \((1/z) = (1/Z) + K\) および \(z = Z + K\) という形に限ると示せ。
(Math. Trip. 1911.)
-
関係 \(z = (1 + Zi)/(Z + i)\) が \(x\) 軸の \(z = 1\) と \(z = -1\) の間の部分を \(Z = 1\) と \(Z = -1\) を通る半円に変形することを示せ。\(x\) 軸のこの部分にこの変形を何度も適用することで得られる図形を全て求めよ。
(Math. Trip. 1912.)
-
もし \(z = 2Z + Z^{2}\) なら、円 \(|Z| = 1\) は \(z\) 平面におけるカージオイドに対応する。
-
\(z = \frac{1}{2}\{Z + (1/Z)\}\) を議論せよ。具体的には円 \(X^{2} + Y^{2} = \alpha^{2}\) が次の楕円に対応することを示せ。この楕円の焦点は \(\alpha\) に関わらず変化しない。 \[ \frac{x^{2}}{\left\{\dfrac{1}{2}\left(\alpha + \dfrac{1}{\alpha}\right)\right\}^{2}} + \frac{y^{2}}{\left\{\dfrac{1}{2}\left(\alpha - \dfrac{1}{\alpha}\right)\right\}^{2}} = 1 \]
-
\((z + 1)^{2} = 4/Z\) のとき、\(z\) 平面上の単位円は \(Z\) 平面上の放物線 \(R\cos^{2} \frac{1}{2}\Theta = 1\) に対応する。円の内側は放物線の外側となる。
-
変換 \(z = \{(Z - ci)/(Z + ci)\}^{2}\) が \(z\) 平面の上半分を \(Z\) 平面上のある半円の内側に対応させることを示せ。
-
\(z = Z^{2} - 1\) とする。\(z\) が円 \(|z| = \kappa\) を表すとき、対応する二つの \(Z\) はカッシーニの卵形線 (Cassinian oval) \(\rho_{1}\rho_{2} = \kappa\) を表す。\(\rho_{1},\ \rho_{2}\) は \(Z\) から \(-1,\ 1\) への長さにそれぞれ等しい。異なる \(\kappa\) の値に対する卵形線を描け。
-
等式 \(az^{2} + 2hzZ + bZ^{2} + 2gz + 2fZ + c = 0\) を考える。対応する \(z\) の値が \(Z\) と等しくなる \(Z\) の値が存在すること、およびその逆を示せ。これらの点をそれぞれ \(Z\) 平面および \(z\) 平面における分岐点 (branch point) と呼ぶ。\(z\) が分岐点を焦点とする楕円を表すとき、\(Z\) も同じ図形を表すことを示せ。
[与えられた等式は一般性を失うことなく \[ z^{2} + 2zZ\cos\omega + Z^{2} = 1 \] と変形できる (自分で確認すること)。それぞれの平面における分岐点は \(\cosec\omega\) と \(-\cosec\omega\) であり、分岐点を焦点とする楕円は次の形で表せる: \[ |z + \cosec\omega| + |z - \cosec\omega| = C \] ここで \(C\) は定数である。問題 9 よりこれは \[ |z + \sqrt{z^{2} - \cosec^{2}\omega}| + |z - \sqrt{z^{2} - \cosec^{2}\omega}| = C \] に等しい。これを \(Z\) で表せば証明すべき命題が示せる]
-
\(m,\ n\) を正の整数、\(a,\ b\) を実数とする。 \(z = aZ^{m} + bZ^{n}\) で \(Z\) が単位円を表すなら、\(z\) はハイポサイクロイド (hypocycloid) またの名をエピサイクロイド (epicycloid) を表す。
-
変換 \[ z = \frac{(a + di)Z_{0} + b}{cZ_{0} - (a - di)} \] を考える。ここで \(a,\ b,\ c,\ d\) は実数で \(a^{2} + d^{2} + bc \gt 0\) が成り立ち、\(Z_{0}\) は \(Z\) の共役を表すとする。この変換が次の円に関する反転に等しいことを示せ: \[ c(x^{2} + y^{2}) - 2ax - 2dy - b = 0 \] 次の条件が成り立つとき、この変換は幾何学的にどう解釈できるか? \[ a^{2} + d^{2} + bc \lt 0 \]
-
変換 \[ \frac{1 - z}{1 + z} = \left(\frac{1 - Z}{1 + Z}\right)^{c} \] を考える。\(c\) が有理数で \(0 \lt c \lt 1\) のとき、この変換で円 \(|z| = 1\) を変換すると角度 \(\pi/c\) の三日月形 (circular lune) の境界が得られる。
-
言うまでもないが、この記号は 例 16.1 と 第二章に関するその他の例 5 で使った \([x]\) とは異なる。[return]
-
厳密に言えば、長さ \(x\) と長さを表す実数 \(x\) の記法も同じように区別する必要がある。そんな区別は衒学的で無駄だと思うかもしれないが、数学を学んでいけば、どんなに強く結びつくものであっても異なっているなら明確に区別しなければならないことを理解できるだろう。クリケットが数学のような科学なら、ウィケットの間のバッツマンの動き、バッツマンの獲得するラン、そしてスコアブックに記録される印を明確に区別することが非常に重要になる。[return]
-
最後の二つの例はウィラード・ギブズ著 Vector Analysis から取った。[return]
-
「実数 (real number)」という言葉は「虚数 (imaginary number)」の逆として作られた。[return]
-
見栄えを考えて \(x + yi\) ではなく \(x + iy\) と書くこともある。[return]
-
訳注: 原文では \(\theta\) を「振幅 (amplitude)」と呼んでいるが、これは標準的ではないので変更した。以降の \(\arg\) も原文では全て \(\text{am}\) となっている。[return]
-
\(|z|\) は \(P\) を極座標で表したときの \(r\) に等しく、極座標のもう一方 \(\theta\) は \(\arg z\) に等しい。ただし \(\theta\) がここで定義される主値であるとは限らない。§22 で定義した極座標は \(0\) から \(2\pi\) の角度を使うが、主値は \(-\pi\) から \(\pi\) なためである。[return]
-
\(\cos \theta + i \sin \theta\) を省略して \(\operatorname{Cis} \theta\) と表記すると便利なことがある。ハークネスとモーレイによって導入されたこの表記を使うと、ド・モアブルの定理は \((\operatorname{Cis}\theta)^{n} = \operatorname{Cis}n\theta\) と表せる。[return]
-
\(a + \sqrt{b},\ a - \sqrt{b}\) という形をした二つの数も「共役」と呼ぶ場合がある (\(a,\ b\) は有理数)。[return]
-
\(\triangle ABC\) の頂点をこの順番でたどると左回りになると仮定している。[return]