第十章 複素数に対する対数関数・指数関数・三角関数
§217 複素数の関数 (その 1)
第三章では複素変数 \[ z = x + iy \] を定義し1、多項式 \(P(z)\) などの \(z\) を使った式のクラスの簡単な性質を考察した。こういった式を \(z\) の関数とみなすのが自然であり、実際多項式 \(P(z)\) と \(Q(z)\) に対する \(P(z)/Q(z)\) は「有理関数」と説明されていた。しかし \(z\) の関数の一般的な定義は与えていない。
複素変数 \(z\) の関数を実変数 \(x\) の関数と同様に定義すればいいと思うかもしれない。つまり \(Z\) が \(z\) の関数であることを、\(z\) と \(Z\) の間に関係が存在して、全てまたは一部の \(z\) に対応する \(Z\) が一つまたは複数存在することとして定義するのである。しかし詳しく考察すると、この定義からは何も得られないことが分かる。というのも、\(z\) が与えられるとき \(x\) と \(y\) も与えられ、その逆も成り立つ: \(z\) に値を割り当てるとは、\(x\) と \(y\) の組に値を割り当てるのと等しい。つまりこの定義における "\(z\) の関数" は 二つの実変数 \(\bm{x}\) と \(\bm{y}\) に関する複素関数 \[ f(x, y) + ig(x, y) \] と同じになる。例えば \[ x - iy,\quad xy,\quad |z| = \sqrt{x^{2} + y^{2}},\quad \arg z = \arctan \frac{y}{x} \] はどれも "\(z\) の関数" となる。この定義に何も問題はないものの、新しい概念を全く定義しておらず、不毛と言える。よって "複素変数 \(z\) の関数" という言葉をもっと制限された意味で使うのが望ましい。つまりこの言葉は二つの実変数 \(x,\ y\) の複素関数からなる一般的なクラスではなく、その一部である特別なクラスを表し、そのクラスに含まれる式は何らかの制限を受けるべきである。しかしこの関数の選び方あるいは特別なクラスに選ばれた関数が持つ性質を説明しようとすると、本書の範囲を超えてしまう。そのため一般的な定義は与えずに、直接的に定義される特殊な関数だけをこれから考えることにする。
§218 複素数の関数 (その 2)
複素数 \(z\) の多項式 (§39)・有理関数 (§46)・根号 (§47) は前に定義した。さらに §26–§27 で数実変数 \(x\) に対して定義した陽および陰の代数関数を複素関数に対して拡張するのも難しくない。これらの全ての場合において、複素数 \(z\) つまり点 \(z\) の引数 (§44) を、関数 \(f(z)\) の引数 (argument) と呼ぶ。この章で私たちの注意を引く問題は、\(z\) の対数関数・指数関数・三角関数の定義と基本的な性質の導出である。これらの関数がこれまで定義されたのは実数の \(z\) に対してだけであり、さらに対数関数では正の値に対してだけだった。
まず対数関数から始める。複素数に対する対数関数は実変数に対する定義 \[ \log x = \int_{1}^{x} \frac{dt}{t}\quad (x \gt 0) \] の拡張としての定義するのが自然であり、このためには積分の概念を拡張したものを少し考える必要がある。
§219 線積分
\(AB\) を次の方程式で定義される曲線の弧 \(C\) とする: \[ x = \phi(t),\quad y = \psi(t) \] ここで \(t\) の関数 \(\phi\) と \(\psi\) は連続な微分係数 \(\phi'\) と \(\psi'\) を持ち、\(t\) が \(t_{0}\) から \(t_{1}\) に変化するとき点 \((x, y)\) は \(A\) から \(B\) へと曲線上を同じ方向に動くとする。
このとき \(x\) と \(y\) の連続関数 \(g,\ h\) に対する線積分 (curvilinear integral) \[ \int_{C} \{g(x, y)\, dx + h(x, y)\, dy\} \qquad \text{(1)} \] を、この積分に対して置換 \(x = \phi(t),\ y = \psi(t)\) を形式的に適用して得られる通常の積分 \[ \int_{t_{0}}^{t_{1}} \{g(\phi, \psi) \phi' + h(\phi, \psi) \psi'\}\, dt \] として定義する。\(C\) を積分路 (path of integration) と呼ぶ。
ここで \[ z = x + iy = \phi(t) + i\psi(t) \] として、\(t\) が変化するときアルガン図において \(z\) が \(C\) の上を動くとする。さらに \[ f(z) = u + iv \] を \(z\) の多項式あるいは \(z\) の有理関数とする。
このとき \[ \int_{C} f(z)\, dz \qquad \text{(2)} \] を \[ \int_{C} (u + iv) (dx + i\, dy) \] として定義する。この積分はさらに次のように定義する: \[ \int_{C} (u\, dx - v\, dy) + i\int_{C} (v\, dx + u\, dy) \]
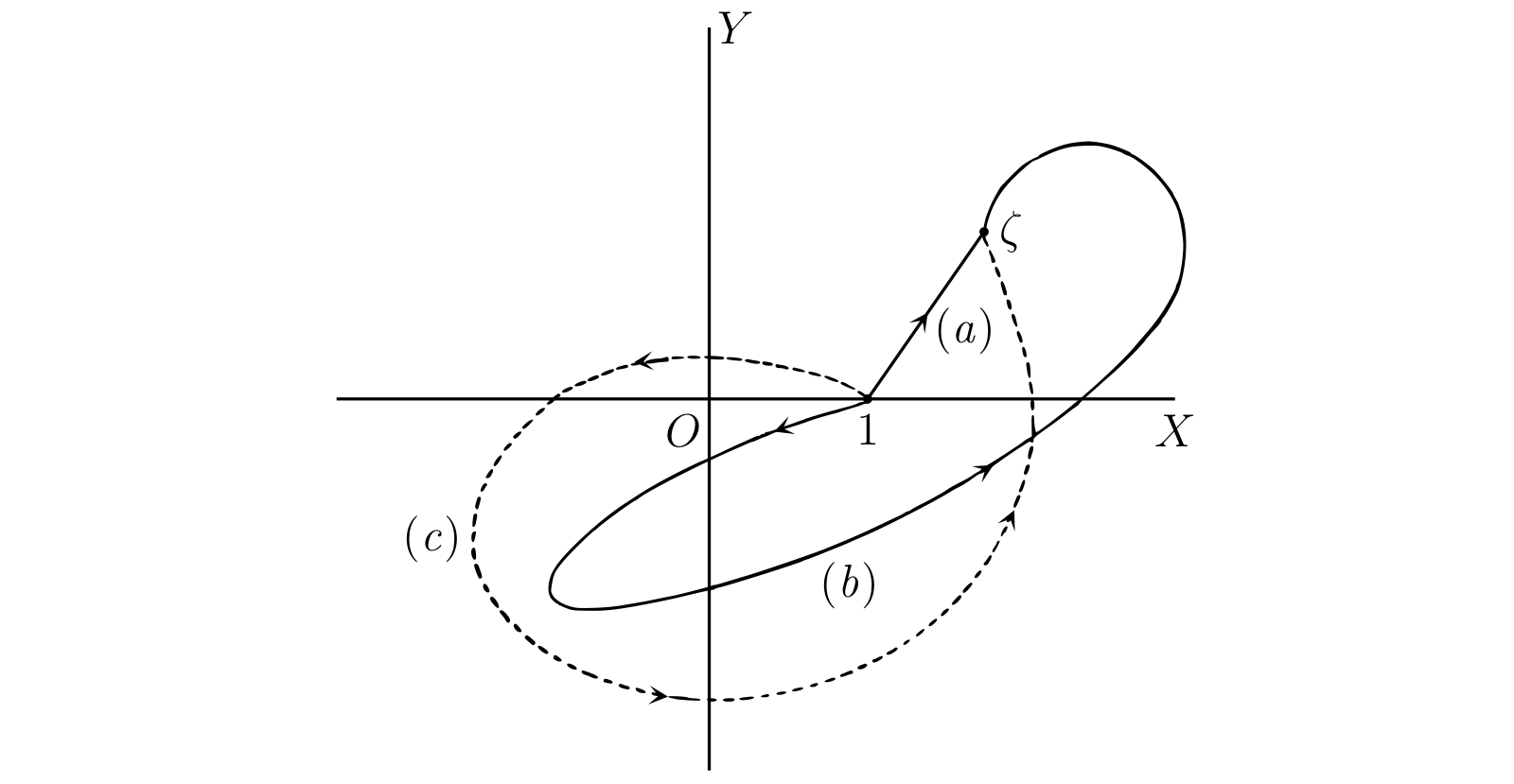
§220 対数関数の定義
\(\zeta = \xi + i\eta\) を任意の複素数とする。一般的な \(\zeta\) の対数 \(\operatorname{Log} \zeta\) を次の等式で定義する: \[ \operatorname{Log} \zeta = \int_{C} \frac{dz}{z} \] ここで \(C\) は \(1\) から始まって \(\zeta\) で終わる、原点を通らない曲線とする。例えば 図 54 の \((a),\ (b),\ (c)\) はどれもこの積分路として利用できる。\(\operatorname{Log} z\) の値は特定の積分路が選ばれたときに定義されるが、今の段階では、こうして定義される \(\operatorname{Log} z\) の値が選ばれる積分路によってどう変化するかは明らかでない。例えば \(\zeta\) が正の実数 \(\xi\) のとき、考えられる積分路の一つとして \(1\) から \(\xi\) への直線がある。方程式 \(x = t,\ y = 0\) で定義されるこの積分路を考えたときの積分は \[ \operatorname{Log} \xi = \int_{1}^{\xi} \frac{dt}{t} \] であり、前章で定義した実数 \(\xi\) の対数 \(\log \xi\) に等しい。つまり \(\xi\) が正の実数なら、\(\operatorname{Log} \xi\) の値の一つが \(\log \xi\) となる。しかしこのとき、そして一般に、積分路には無数の選択肢がある。全ての \(\operatorname{Log} \xi\) が \(\log \xi\) に等しい証拠はなく、後で見るように実際のところ等しくない。表記を \(\log \zeta\) や \(\log \xi\) ではなく \(\operatorname{Log} \zeta\) および \(\operatorname{Log} \xi\) としたのはこのためである。\(\operatorname{Log} \xi\) は多値 (の可能性がある) 関数であり、\(\log \xi\) はその値の一つに過ぎない。今の私たちが持っている知識で考えるとき、一般の \(\operatorname{Log} \zeta\) の値について次の三つの可能性がある:
- \(1\) から \(\zeta\) へのどの路を選んでも同じになる。
- 全ての異なる路に対して異なる値が得られる。
- 特定の路のクラスごとに対応する値が存在する。
これらのどれが正しくどれが間違っているかは定義を見ても全く分からない。
§221 対数関数の値
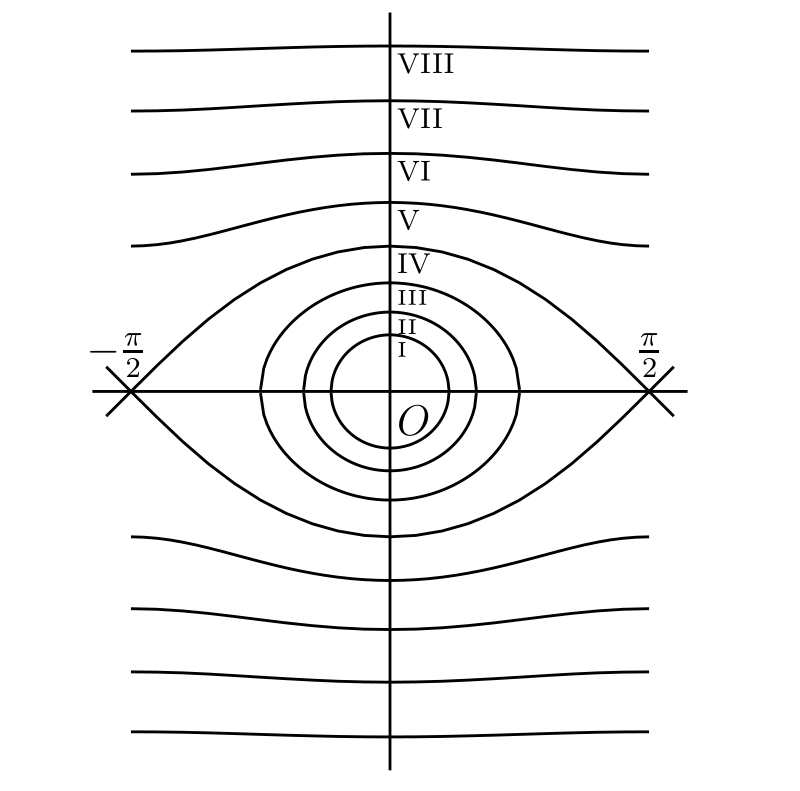
点 \(z = \zeta\) の極座標が \((\rho, \phi)\) で \[ \zeta = \rho(\cos\phi + i\sin\phi) \] が成り立つとして、さらに \(-\pi \lt \phi \lt \pi\) で \(\rho\) は正とする。このとき \(\zeta\) は \(0\) と負の実数以外の全ての値を取る。
路 \(C\) における任意の点の座標 \((x, y)\) は \(t\) の関数であり、その極座標 \((r, \theta)\) も \(t\) の関数である。また §219 の定義からは \[ \operatorname{Log} \zeta = \int_{C} \frac{dz}{z} = \int_{C} \frac{dx + i\, dy}{x + iy} = \int_{t_{0}}^{t_{1}} \frac{1}{x + iy} \left(\frac{dx}{dt} + i\frac{dy}{dt}\right) dt \] が分かる。一方で \(x = r\cos\theta,\ y = r\sin\theta\) だから \[ \begin{aligned} \frac{dx}{dt} + i\frac{dy}{dt} & = \left(\cos\theta\, \frac{dr}{dt} - r\sin\theta\, \frac{d\theta}{dt}\right) + i\left(\sin\theta\, \frac{dr}{dt} + r\cos\theta\, \frac{d\theta}{dt}\right) \\ & = (\cos\theta + i\sin\theta) \left(\frac{dr}{dt} + ir\frac{d\theta}{dt}\right) \end{aligned} \] が成り立つ。よって \[ \operatorname{Log} \zeta = \int_{t_{0}}^{t_{1}} \frac{1}{r}\, \frac{dr}{dt}\, dt + i\int_{t_{0}}^{t_{1}} \frac{d\theta}{dt}\, dt = [\log r] + i[\theta] \] である。ここで \([\log r]\) は \(t = t_{1}\) と \(t = t_{0}\) に対応する点における \(\log r\) の値の差を表し、\([\theta]\) も同様とする。
実部 \([\log r]\) に関しては \[ [\log r] = \log \rho - \log 1 = \log \rho \] が明らかに分かる。しかし虚部 \([\theta]\) についてはさらに議論が必要となる。まず積分路が \(1\) と \(\zeta\) を結ぶ直線の場合を考える。最初の \(\theta\) の値は \(1\) の偏角、正確には \(1\) の偏角の一つであり、整数 \(k\) を使って \(2k\pi\) と表せる。最初の値を \(\theta = 2k\pi\) としよう。すると \(t\) が直線上を移動するとき、\(\theta\) は \(2k\pi\) から \(2k\pi + \phi\) に増加する。よって \[ [\theta] = (2k\pi + \phi) - 2k\pi = \phi \] となる。つまり積分路が直線なら \(\operatorname{Log} \zeta = \log \rho + i\phi\) が成り立つ。

この \(\operatorname{Log} \zeta\) の値を主値 (principal value) と呼ぶ。\(\zeta = \rho\) かつ \(\phi = 0\) で \(\zeta\) が正の実数なら \(\operatorname{Log} \zeta\) の主値は通常の \(\log \zeta\) に等しいので、\(\operatorname{Log} \zeta\) の主値を \(\log \zeta\) と表記すれば一貫性が保たれる。よって \[ \log \zeta = \log \rho + i\phi \] と定めるのが理にかなっている。主値は虚部 \(\phi\) が \(-\pi\) と \(\pi\) の間にあるという事実によって特徴付けられる。
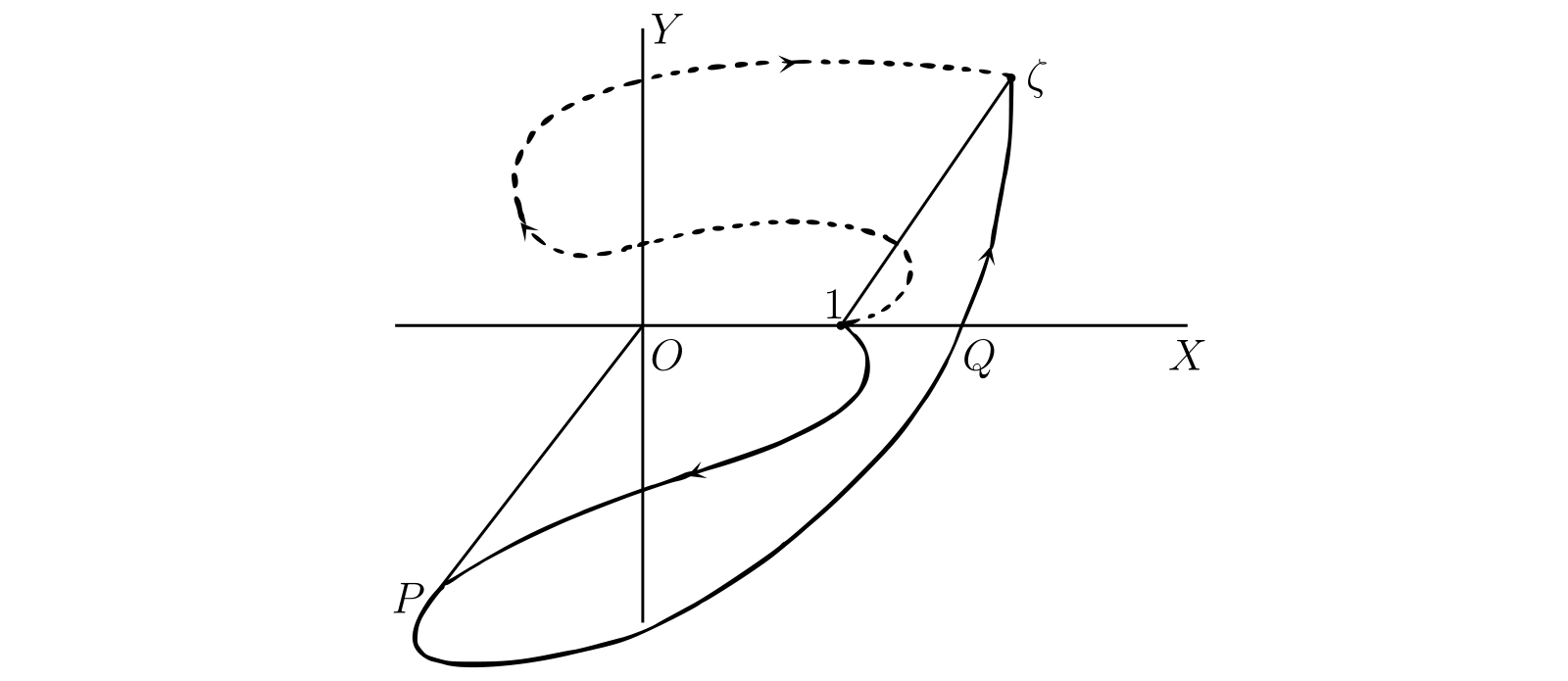
続いて 図 56 のように、\(1\) と \(\zeta\) を結ぶ直線と積分路が囲む領域が原点を含まない場合を考える。\([\theta]\) がこの場合にも \(\phi\) に等しいことは容易に分かる。例えば図中の実線で書かれた積分路では、最初 \(2k\pi\) に等しい \(\theta\) はまず \[ 2k\pi - \angle XOP \] まで減少し、それから増加する。\(\theta\) は点 \(Q\) で \(2k\pi\) に等しくなり、最終的に \(2k\pi + \phi\) となる。破線の積分路では多少複雑になるが、結論は変わらない。ここでは直線と曲線が二つの領域を囲むが、原点は含まない。つまり \(\bm{1}\) と \(\bm{\xi}\) を結んだ直線と積分路からなる閉曲線が原点を含まないなら \[ \bm{\operatorname{Log} \zeta = \log \zeta = \log \rho + i\phi} \] が成り立つ。
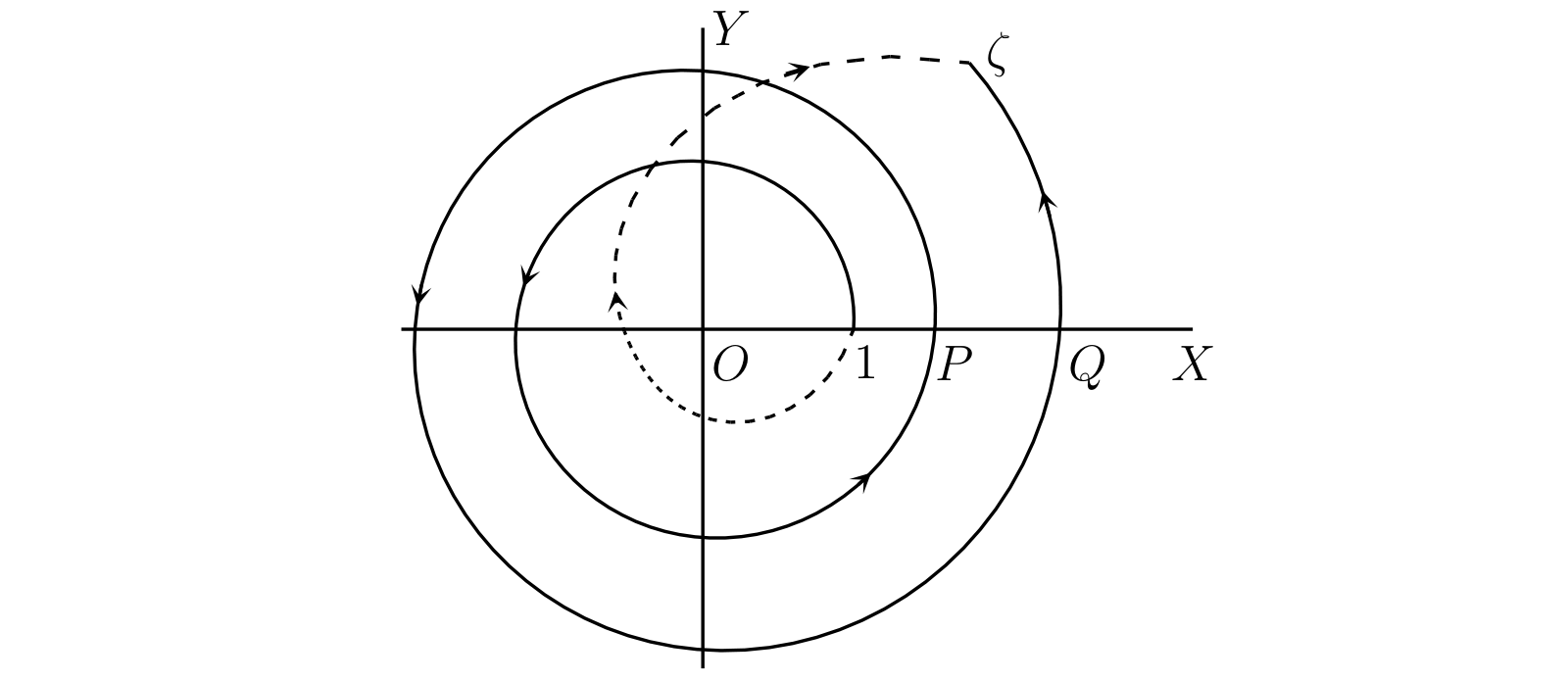
一方で \([\theta]\) が \(\phi\) と等しくならない積分路も簡単に構成できる。例として 図 57 中の実線で示される曲線を考える。\(\theta\) が最初 \(2k\pi\) に等しいとすれば、\(\theta\) は \(P\) に着くまでに \(2\pi\) 増加し、\(Q\) に着くまでに \(4\pi\) 増加する。最終的な \(\theta\) の値は \(2k\pi + 4\pi + \phi\) であり、\([\theta] = 4\pi + \phi\) が得られる。つまりこの積分路を使うと \[ \operatorname{Log} \zeta = \log \rho + i(4\pi + \phi) \] となる。
この場合には積分路が原点の周りを正方向に二回周回する。原点の周りを \(k\) 回周回する路が積分路なら、全く同じ議論によって \([\theta] = 2k\pi+ \phi\) つまり \[ \operatorname{Log} \zeta = \log \rho + i(2k\pi + \phi) \] が分かる。またこの等式で \(k\) は正となっているが、図 57 の破線ように原点の周りを逆方向に周回する積分路を考えれば \(k\) を負とした値も全て得られる。\(|\zeta| = \rho\) で \(2k\pi + \phi\) は \(\arg \zeta\) の異なる値だから、\(\log |\zeta| + i\arg \zeta\) の全ての値が \(\operatorname{Log} \zeta\) だと結論できる。さらにここまでの議論から、\(\operatorname{Log} \zeta\) の全ての値がこの形だとも分かる。
以上を次にまとめる:
\(\operatorname{Log} \zeta\) の一般的な値は \[ \log |\zeta| + i\arg \zeta = \log \rho + i(2k\pi + \phi) \] である。ここで \(k\) は正または負の整数を表し、その値は積分路によって決定される。積分路が直線なら \(k = 0\) であり、次が成り立つ: \[ \operatorname{Log} \zeta = \log \zeta = \log \rho + i\phi \]
ここまでの議論では \(\zeta\) が関数 \(\operatorname{Log}\) の引数で、\((\xi, \eta)\) と \((\rho, \phi)\) が \(\zeta\) の座標、\(z\) が積分路上の点、\((x, y)\) と \((r, \theta)\) が \(z\) の座標としてきた。しかし \(\operatorname{Log}\) の引数を通常通り \(z\) で表してはいけない理由はないため、次の例からは \(\operatorname{Log} z\) を使うことにする。
-
上の議論では \(-\pi \lt \theta \lt \pi\) を仮定したので、\(z\) が負の実数の場合は除かれていた。\(z\) が負の実数だと \(1\) と \(z\) を結ぶ直線が \(0\) を通るために、この直線を積分路とした積分を計算できない。\(\pi\) と \(-\pi\) はどちらも \(\arg z\) で \(\theta\) はどちらかと等しい。また \(r = -z\) である。この場合でも \(\operatorname{Log} z\) は \(\log |z| + i\arg z\) に等しく、整数 \(k\) を使って \[ \log (-z) + (2k + 1)\pi i \] と表せる。\(\log (-z) + \pi i\) と \(\log (-z) - \pi i\) という値はそれぞれ \(1\) と \(z\) を結ぶ積分路であって常に \(x\) 軸より上および下にあるものに対応する。都合に応じてどちらでも \(\operatorname{Log} z\) の主値とみなすことができる。本書では \(x\) 軸よりも上を通る積分路に対応する \(\log (-z) + i\pi\) を主値として採用する。
-
\(\operatorname{Log} z\) の任意の値の実部および虚部は \(x\) と \(y\) の連続関数である。ただし \(x = 0,\ y = 0\) は除く。
-
\(\bm{\operatorname{Log} z}\) の満たす関数方程式: 関数 \(\operatorname{Log} z\) は次の方程式を満たす: \[ \operatorname{Log} z_{1} z_{2} = \operatorname{Log} z_{1} + \operatorname{Log} z_{2} \qquad \text{(1)} \] この等式は左辺または右辺の全ての値がもう一方のある値に等しくなるという意味で成り立つ。証明は \[ z_{1} = r_{1}(\cos\theta_{1} + i\sin\theta_{1}),\quad z_{2} = r_{2}(\cos\theta_{2} + i\sin\theta_{2}) \] とおいて §221 の結果を使う。ただし \[ \log z_{1}z_{2} = \log z_{1} + \log z_{2} \qquad \text{(2)} \] が常に成り立つとは限らない。例えば \[ z_{1} = z_{2} = \dfrac{1}{2}(-1 + i\sqrt{3}) = \cos \dfrac{2}{3}\pi + i \sin \dfrac{2}{3}\pi \] のとき \(\log z_{1} = \log z_{2} = \frac{2}{3}\pi i\) および \(\log z_{1} + \log z_{2} = \frac{4}{3}\pi i\) だが、\(\frac{4}{3}\pi i\) は \(\operatorname{Log} z_{1}z_{2}\) の値の一つであるものの主値ではない。主値は \(\log z_{1}z_{2} = -\frac{2}{3}\pi i\) である。
\(\text{(1)}\) のように片側の全ての値がもう一方のとある値になり、その逆も成り立つ等式を完全な等式 (complete equation) あるいは完全に正しい (completely true) 等式と呼ぶ。
-
整数 \(m\) に対する等式 \(\operatorname{Log} z^{m} = m\operatorname{Log} z\) は完全には正しくない。右辺の値は全て左辺のとある値となるが、逆は正しくない。
-
等式 \(\operatorname{Log} (1/z) = -\operatorname{Log} z\) は完全に正しい。また \(z\) が負の実数でなければ \(\log (1/z) = -\log z\) も成り立つ。
-
等式 \[ \log \left(\frac{z - a}{z - b}\right) = \log (z - a) - \log (z - b) \] が正しくなるのは、点 \(z = a\) と \(z = b\) を結ぶ直線と、これらの点を通り \(x\) 軸負方向に無限に延びる二直線によって囲まれる領域の外側に \(z\) があるときである。
-
等式 \[ \log \left(\frac{a - z}{b - z}\right) = \log \left(1 - \frac{a}{z}\right) - \log \left(1 - \frac{b}{z}\right) \] は \(z\) が三点 \(O,\ a,\ b\) からなる三角形の外側にあるとき正しい。
-
実数変数 \(x\) の関数 \(\operatorname{Im}(\operatorname{Log} x)\) のグラフを描け。 [このグラフは \(y = 2k\pi\) の正の部分と \(y = (2k + 1)\pi\) の負の部分からなる]
-
等式 \[ \pi f(x) = p\pi + (q - p)\operatorname{Im}(\log x) \] で定義される実変数 \(x\) の関数 \(f(x)\) は \(x\) が正のとき \(p\) に等しく、\(x\) が負のとき \(q\) に等しい。
-
等式 \[ \pi f(x) = p\pi + (q - p)\operatorname{Im}\{\log(x - 1)\} + (r - q)\operatorname{Im}(\log x) \] で定義される関数 \(f(x)\) は \(x \gt 1\) で \(p\) に等しく、\(0 \lt x \lt 1\) で \(q\) に等しく、\(x \lt 0\) で \(r\) に等しい。
-
(i) \(\log z\) と (ii) \(\operatorname{Log} z\) の値が (a) 実数あるいは (b) 純虚数になる \(z\) の値はそれぞれ何か?
-
\(z = x + iy\) なら \(\operatorname{Log}\operatorname{Log} z = \log R + i(\Theta + 2k'\pi)\) が成り立つ。ここで \[ R^{2} = (\log r)^{2} + (\theta + 2k\pi)^{2} \] であり、\(\Theta\) は次の等式を満たす最小の正の角度である: \[ \cos\Theta : \sin\Theta : 1 = \log r : \theta + 2k\pi: \sqrt{(\log r)^{2} + (\theta + 2k\pi)^{2}} \] 二重に無限に存在する \(\operatorname{Log}\operatorname{Log}(1 + i\sqrt{3})\) を大まかにプロットせよ。\(\log\operatorname{Log}(1 + i \sqrt{3})\) と \(\operatorname{Log}\log(1 + i\sqrt{3})\) がどれに対応するか示せ。
§222 指数関数の定義
第九章では実数変数 \(y\) の関数 \(e^{y}\) を \(y = \log x\) の逆関数として定義した。ここから複素変数 \(z\) の関数 \(\operatorname{Log} z\) の逆関数の定義が自然に導かれる:
\(\operatorname{Log} z\) のいずれかの値が \(\zeta\) に等しいなら、\(z\) を \(\zeta\) の指数 (exponential) と呼び \[ z = \exp \zeta \] と書く。
つまり \(z = \exp \zeta\) となるのは \(\zeta = \operatorname{Log} z\) が成り立つときとなる。固定された \(z\) に対応する \(\zeta\) が無限に存在するのは明らかである。ここから逆に、固定された \(\zeta\) に対応する \(z\) が無限に存在する、つまり \(\exp \zeta\) が \(\zeta\) の無限多価関数だと考えてもおかしくはない。しかし次の定理が示す通りこの考えは間違っている:
\(\exp \zeta\) は \(\zeta\) の一価関数である。
証明は次の通り。\(\exp \zeta\) の値を \[ z_{1} = r_{1}(\cos\theta_{1} + i\sin\theta_{1}),\quad z_{2} = r_{2}(\cos\theta_{2} + i\sin\theta_{2}) \] とする。このとき \[ \zeta = \operatorname{Log} z_{1} = \operatorname{Log} z_{2} \] が成り立つから、整数 \(m,\ n\) を使って \[ \log r_{1} + i(\theta_{1} + 2m\pi) = \log r_{2} + i(\theta_{2} + 2n\pi) \] と書ける。ここから \[ \log r_{1} = \log r_{2},\quad \theta_{1} + 2m\pi = \theta_{2} + 2n\pi \] が分かる。つまり \(r_{1} = r_{2}\) で、\(\theta_{1}\) と \(\theta_{2}\) は \(2\pi\) の倍数だけ離れている。よって \(z_{1} = z_{2}\) が成り立つ。
\(\zeta\) が実数なら \(\exp \zeta = e^{\zeta}\) であり、\(\exp \zeta\) は 第九章 で定義した実数に対する指数関数に等しい。
\(z = e^{\zeta}\) なら \(\log z = \zeta\) が成り立つ。つまり \(\operatorname{Log} z\) の値の一つが \(\zeta\) だから、\(z = \exp \zeta\) を得る。
§223 指数関数の値
\(\zeta = \xi + i\eta\) として \[ z = \exp \zeta = r(\cos\theta + i\sin\theta) \] を考える。このとき任意の整数 \(m\) に対して \[ \xi + i\eta = \operatorname{Log} z = \log r + i(\theta + 2m\pi) \] が成り立つ。よって \(\xi = \log r,\ \eta = \theta + 2m\pi\) であり、これは \[ r = e^{\xi},\quad \theta = \eta - 2m\pi \] を意味する。よって \[ \exp (\xi + i\eta) = e^{\xi} (\cos\eta + i\sin\eta) \] を得る。
\(\eta = 0\) なら §222 で見た通り \(\exp \xi = e^{\xi}\) となる。また明らかに、\(\exp (\xi + i\eta)\) の実部および虚部は全ての \(\xi\) と \(\eta\) に対して連続となる。
§224 \(\exp ζ\) が満たす関数方程式
\(\zeta_{1} = \xi_{1} + i\eta_{1}\) および \(\zeta_{2} = \xi_{2} + i\eta_{2}\) とすると \[ \begin{aligned} \exp \zeta_{1} × \exp \zeta_{2} & = e^{\xi_{1}} (\cos\eta_{1} + i\sin\eta_{1}) × e^{\xi_{2}} (\cos\eta_{2} + i\sin\eta_{2}) \\ & = e^{\xi_{1}+\xi_{2}} \{\cos(\eta_{1} + \eta_{2}) + i\sin(\eta_{1} + \eta_{2})\} \\ & = \exp(\zeta_{1} + \zeta_{2}) \end{aligned} \] が成り立つ。つまり指数関数は関数方程式 \(f(\zeta_{1} + \zeta_{2}) = f(\zeta_{1}) f(\zeta_{2})\) を満たす。実数の \(\zeta_{1}\) と \(\zeta_{2}\) に対するこの方程式は前に (§205 で) 示した。
§225 一般的な指数 \(a^{x}\) の定義
実数では \(\exp \zeta = e^{\zeta}\) だったから、複素数 \(\zeta\) に対してもこの記法を採用して \(\exp\) は使わないようにできると思うかもしれない。しかし \(e^{\zeta}\) にはより一般的な定義を与えなければならないので、この方針は取らない。これから見るように \(e^{\zeta}\) は無限に多くの値を取る関数であり、\(\exp \zeta\) はその一つに過ぎない。
これまでの議論で、ときには何種類かの方法を使って次の式に意味を与えた: \[ 3^{1/2},\quad (-1)^{1/3},\quad (\sqrt{3} + \dfrac{1}{2}i)^{-1/2},\quad (3.5)^{1+\sqrt{2}} \] しかし次の式に意味を与える定義は示していない: \[ (1 + i)^{\sqrt{2}},\quad 2^{i},\quad (3 + 2i)^{2+3i} \] 私たちはこれから \(a^{\zeta}\) に一般的な定義を与える。この定義は実数および複素数の \(a\) と \(\zeta\) に適用でき、唯一 \(a\) が \(0\) であってはいけないという制限がある。
関数 \(a^{\zeta}\) は次の等式で定義される: \[ a^{\zeta} = \exp (\zeta\operatorname{Log} a) \] \(\operatorname{Log} a\) は任意の \(a\) の対数を表す。
この定義がこれまでの定義と矛盾せず、かつ特殊ケースとしてそれらを含むことを確認する必要がある:
- \(a\) が正で \(\zeta\) が実数なら、\(\zeta\operatorname{Log} a\) の値の一つ \(\zeta\log a\) は実数で \(\exp (\zeta\log a) = e^{\zeta\log a}\) が成り立つ。これは第九章の定義と矛盾せず、以前に第九章の定義は初等代数の定義と矛盾しないと示した。よってこの定義も同様である。
- \(a = e^{\tau} (\cos\psi + i\sin\psi)\) なら任意の整数 \(m\) と有理数 \(p/q\) に対して \[ \begin{gathered} \operatorname{Log} a = \tau + i(\psi + 2m\pi), \\ \exp \{(p/q)\operatorname{Log} a\} = e^{p\tau/q} \operatorname{Cis} \{(p/q)(\psi + 2m\pi)\} \end{gathered} \] が成り立つ。容易に分かるように、\(m\) が全ての整数値を取るときこの式はちょうど \(q\) 個の異なる値を取り、これは §48 で定義した \(a^{p/q}\) と等しい。よってこの定義は第三章で定義したものと矛盾しない。
§226 一般的な指数 \(a^{x}\) の値
\(-\pi \lt \psi \leq \pi\) に対して \[ \zeta = \xi + i\eta,\quad a = \sigma(\cos\psi + i\sin\psi) \] であり、§225 の表記で \(\sigma = e^{\tau}\) つまり \(\tau = \log \sigma\) だとする。
このとき \[ \zeta \operatorname{Log} a = (\xi + i\eta)\{\log \sigma + i(\psi + 2m\pi)\} = L + iM \] とすれば \[ L = \xi \log \sigma - \eta(\psi + 2m\pi),\quad M = \eta\log \sigma + \xi (\psi + 2m\pi) \] であり、 \[ a^{\zeta} = \exp(\zeta\operatorname{Log} a) = e^{L}(\cos M + i\sin M) \] が成り立つ。よって \(a^{\zeta}\) の一般的な値は \[ e^{\xi\log \sigma - \eta(\psi+2m\pi)} [\cos\{\eta\log \sigma + \xi(\psi + 2m\pi)\} + i\sin\{\eta\log \sigma + \xi(\psi + 2m\pi)\}] \] である。
一般に \(a^{\zeta}\) は無限多価関数となる。実際 \[ |a^{\zeta}| = e^{\xi\log \sigma - \eta(\psi+2m\pi)} \] は \(\eta = 0\) でなければ全ての \(m\) に対して異なる値を持つ。一方でもし \(\eta = 0\) なら、\(a^{\zeta}\) の全ての異なる値は大きさが同じになる。二つの \(a^{\zeta}\) の値が等しいとき、大きさが等しいのに加えて偏角が等しいか \(2\pi\) の倍数だけ離れる。そのためには異なる整数 \(m,\ n\) で \(\xi(\psi + 2m\pi)\) と \(\xi(\psi + 2n\pi)\) が \(2\pi\) の倍数だけ離れることが必要であり、もし \[ \xi(\psi + 2m\pi) - \xi(\psi + 2n\pi) = 2k\pi \] なら \(\xi = k/(m - n)\) は有理数となる。よって \(\bm{\zeta}\) が実数の有理数である場合を除いて \(\bm{a^{\zeta}}\) は無限個の値を持つと結論できる。この命題の裏「\(\zeta\) が実数の有理数なら \(a^{\zeta}\) は有限個の値しか取らない」は前に見た。
\(a^{\zeta} = \exp (\zeta\operatorname{Log} a)\) の主値は \(\operatorname{Log} a\) を主値とすることで得られる。つまり上の一般的な公式で \(m = 0\) とすればよい。具体的に言えば \(a^{\zeta}\) の主値は \[ e^{\xi\log \sigma - \eta\psi} \{\cos(\eta\log \sigma + \xi\psi) + i\sin(\eta\log \sigma + \xi\psi)\} \] である。
特に興味深い場合が二つある。一つは \(a\) が正の実数で \(\zeta\) が実数のときで、このとき \(\sigma = a,\ \) \(\psi = 0,\ \) \(\xi = \zeta,\ \) \(\eta = 0\) より \(a^{\zeta}\) の主値は \(e^{\zeta\log a}\) となり、前章で定義した値と一致する。もう一つは \(|a| = 1\) で \(\zeta\) が実数のときで、このとき \(\sigma = 1,\ \) \(\xi = \zeta,\ \) \(\eta = 0\) より \((\cos\psi + i\sin\psi)^{\zeta}\) の主値は \(\cos\zeta\psi + i\sin\zeta\psi\) となる。これはド・モアブルの定理 (§45–§49 ) のさらなる一般化と言える。
-
\(i^{i}\) の値を求めよ。 [定義から \(i^{i} = \exp (i\operatorname{Log} i)\) が分かる。一方で任意の整数 \(k\) に対して \[ i = \cos \dfrac{1}{2}\pi + i\sin \dfrac{1}{2}\pi,\quad \operatorname{Log} i = (2k + \dfrac{1}{2})\pi i \] だから、 \[ i^{i} = \exp\{-(2k + \dfrac{1}{2})\pi\} = e^{-(2k + \frac{1}{2})\pi} \] が分かる。全ての \(i^{i}\) の値は正の実数である]
-
\((1 + i)^{i},\ i^{1+i},\ (1 + i)^{1+i}\) の値を全て求めよ。
-
\(a^{\zeta}\) の値をアルガン図にプロットすると対数螺旋に内接する等角多角路になり、その角度は \(a\) に依存しないことを示せ。
(Math. Trip. 1899.)
[\(a^{\zeta} = r(\cos\theta + i\sin\theta)\) なら次が成り立つ: \[ r = e^{\xi\log \sigma - \eta(\psi + 2m\pi)},\quad \theta = \eta\log \sigma + \xi(\psi + 2m\pi) \] よって \(a^{\zeta}\) に対応する点は全て螺旋 \(r = \sigma^{(\xi^{2} + \eta^{2})/\xi} e^{-\eta \theta/\xi}\) 上にある]
-
関数 \(\bm{e^{\zeta}}\): 一般的な等式で \(a = e\) とすれば \(\log \sigma = 1\) および \(\psi = 0\) だから、 \[ e^{\zeta} = e^{\xi-2m\pi\eta} \{\cos(\eta + 2m\pi\xi) + i\sin(\eta + 2m\pi\xi)\} \] となる。\(e^{\zeta}\) の主値は \(e^{\xi}(\cos\eta + i\sin\eta)\) であり、これは \(\exp \zeta\) (§223) に等しい。特に \(\zeta\) が実数で \(\eta = 0\) なら一般に \[ e^{\zeta} (\cos 2m\pi\zeta + i\sin 2m\pi\zeta) \] で主値は \(e^{\zeta}\) となる。ここで \(e^{\zeta}\) は第九章で定義した正の指数を表す。
-
\(\operatorname{Log} e^{\zeta} = (1 + 2m\pi i)\zeta + 2n\pi i\) を示せ。\(m\) と \(n\) は任意の整数とする。一般に \(\operatorname{Log} a^{\zeta}\) が二重に無限の値を持つと示せ。
-
等式 \(1/a^{\zeta} = a^{-\zeta}\) は完全に正しく (例 93.3)、主値でも正しい。
-
等式 \(a^{\zeta} × b^{\zeta} = (ab)^{\zeta}\) は完全に正しいが、主値では成り立たない場合がある。
-
等式 \(a^{\zeta} × a^{\zeta'} = a^{\zeta+\zeta'}\) は完全には正しくないが、主値では正しい。 [全ての右辺の値は左辺の値になるが、一般に \(a^{\zeta} × a^{\zeta'}\) すなわち \[ \exp \{\zeta(\log a + 2m\pi i) + \zeta'(\log a + 2n\pi i)\} \] は \(a^{\zeta+\zeta'}\) の値とならない。\(m = n\) の場合に限って \(a^{\zeta+\zeta'}\) の値となる]
-
次の等式に関する同様の結果は何か? \[ \operatorname{Log} a^{\zeta} = \zeta\operatorname{Log} a,\quad (a^{\zeta})^{\zeta'} = (a^{\zeta'})^{\zeta} = a^{\zeta\zeta'} \]
-
\(e^{\zeta}\) の (a) 任意の値および (b) 主値が (i) 実数 (ii) 純虚数 (iii) 大きさ \(1\) となる \(\zeta\) の値はそれぞれ何か?
-
\(a^{\zeta}\) が全て実数となるための必要十分条件は、\(2\xi\) と \(\{\eta\log |a| + \xi\arg a\}/\pi\) が両方とも整数になることである。ここで \(\arg a\) は任意の偏角とする。全ての値が大きさ \(1\) となるための必要十分条件は何か?
-
\(x \gt 0\) に対する \(|x^{i} + x^{-i}|\) の一般的な値は \[ e^{-(m-n)\pi} \sqrt{2\{\cosh 2(m + n)\pi + \cos(2\log x)\}} \] である。
-
次の議論の誤謬を指摘せよ: 整数 \(m,\ n\) に対して \(e^{2m\pi i} = e^{2n\pi i} = 1\) が成り立つから、両辺を \(i\) 乗して \(e^{-2m\pi} = e^{-2n\pi}\) を得る。
-
実数 \(x\) に対して \(x^{x}\) のいずれかの値が実数となるのはどんなときか? [\(x \gt 0\) なら \[ x^{x} = \exp (x\operatorname{Log} x) = \exp (x\log x) \operatorname{Cis} 2m\pi x \] が成り立つ。最初の部分は実数だから、\(m = 0\) とした主値は常に実数となる。
\(x\) が無理数または \(p/(2q + 1)\) の形をした有理数なら、これ以外に実数値はない。しかし \(x\) が \(p/2q\) という形をした有理数なら、\(m = q\) が \(-\exp (x\log x)\) というもう一つの実数値を与える。
\(x = -\xi \lt 0\) なら \[ x^{x} = \exp \{-\xi\operatorname{Log} (-\xi)\} = \exp (-\xi\log \xi) \operatorname{Cis}\{-(2m + 1)\pi\xi\} \] であり、\(\xi = p/(2q + 1)\) なら実数の \(x^{x}\) の値が存在する。それは \(m = q\) のときで、値は \[ \exp (-\xi\log \xi) \operatorname{Cis} (-p\pi) = (-1)^{p} \xi^{-\xi} \] となる。具体例を次に示す: \[ \left(\dfrac{1}{3}\right)^{1/3} = \sqrt[3]{\dfrac{1}{3}},\quad \left(\dfrac{1}{2}\right)^{\frac{1}{2}} = ±\sqrt{\dfrac{1}{2}},\quad \left(-\dfrac{2}{3}\right)^{-\frac{2}{3}} = \sqrt[3]{\dfrac{9}{4}},\quad \left(-\dfrac{1}{3}\right)^{-\frac{1}{3}} = -\sqrt[3]{3}] \]
-
任意の底の対数: \(\zeta = \operatorname{Log}_{a} z\) を定義する方法は二つある。\(a^{\zeta}\) の主値が \(z\) のとき \(\zeta = \operatorname{Log}_{a} z\) とする方法と、\(a^{\zeta}\) のいずれかが \(z\) のとき \(\zeta = \operatorname{Log}_{a} z\) とする方法である。
\(a = e\) のときを考えると、最初の定義では \(e^{\zeta}\) の主値が \(z\) に等しいとき、つまり \(\exp \zeta = z\) のとき \(\zeta = \operatorname{Log}_{e} z\) となる。つまり \(\operatorname{Log}_{e} z\) は \(\operatorname{Log} z\) と等しくなる。一方で二つ目の定義で \(\zeta = \operatorname{Log}_{e} z\) となるのは \[ e^{\zeta} = \exp (\zeta\operatorname{Log} e) = z,\quad \zeta\operatorname{Log} e = \operatorname{Log} z \] つまり \(\zeta = (\operatorname{Log} z)/(\operatorname{Log} e)\) のときであり、二つの対数は任意の値を取れる。言い換えれば \[ \zeta = \operatorname{Log}_{e} z = \frac{\log |z| + (\arg z + 2m\pi)i}{1 + 2n\pi i} \] であり、\(\zeta\) は二重に無限の値を取る多価関数となる。この定義では一般に \(\operatorname{Log}_{a} z = (\operatorname{Log} z)/(\operatorname{Log} a)\) となる。
-
任意の整数 \(m\) と \(n\) に対して \(\operatorname{Log}_{e} 1 = \dfrac{2m\pi i}{1 + 2n\pi i}\) と \(\operatorname{Log}_{e}(-1) = \dfrac{(2m + 1)\pi i}{1 + 2n\pi i}\) が成り立つ。
§227 サインとコサインの指数を使った表現
等式 \[ \exp (\xi + i\eta) = \exp \xi(\cos\eta + i\sin\eta) \] からは重要な公式をいくつも導出できる。\(\xi = 0\) とすると \(\exp (i\eta) = \cos\eta + i\sin\eta\) を得る。\(\eta\) の符号を変えれば \(\exp (-i\eta) = \cos\eta - i\sin\eta\) であり、ここから \[ \cos\eta = \dfrac{1}{2} \{\exp (i\eta) + \exp (-i\eta)\},\quad \sin\eta = -\dfrac{1}{2}i\{\exp (i\eta) - \exp (-i\eta)\} \] が分かる。これを使えば任意の \(\eta\) の三角比に対する \(\exp (i\eta)\) を使った表現を導ける。
§228 \(\sin\) と \(\cos\) の定義
前節では実数 \(\zeta\) に対して \[ \begin{alignedat}{5} \cos\zeta & = & & \dfrac{1}{2} & & \{\exp (i\zeta) + \exp (-i\zeta)\}, & &\\ \sin\zeta & = -& & \dfrac{1}{2}i& & \{\exp (i\zeta) - \exp (-i\zeta)\} & & \end{alignedat} \] が成り立つことを見た。
二つの等式の左辺は初等三角法で採用される通常の幾何学的な定義で定義されており、実数の \(\zeta\) に対してのみ定義される。一方で左辺は実数および複素数の全ての \(\zeta\) に対して定義される。よって \(\text{(1)}\) を全ての \(\zeta\) に対する \(\cos \zeta\) と \(\sin \zeta\) の定義として自然に採用できる。§227 よりこの定義は実数に対する初等的な定義と一致する。
\(\cos \zeta\) と \(\sin \zeta\) が定義できれば、他の三角比は次の等式で定義できる: \[ \tan \zeta = \frac{\sin \zeta}{\cos \zeta},\quad \cot \zeta = \frac{\cos \zeta}{\sin \zeta},\quad \sec \zeta = \frac{1}{\cos \zeta},\quad \cosec \zeta = \frac{1}{\sin \zeta} \qquad \text{(2)} \] \(\cos \zeta,\ \sec \zeta\) が偶関数であり、\(\sin \zeta,\ \tan \zeta,\ \cot \zeta,\ \cosec \zeta\) が奇関数であることが定義から分かる。また \(\exp (i\zeta) = t\) とすれば \[ \begin{gathered} \cos \zeta = \dfrac{1}{2} \{t + (1/t)\},\quad \sin \zeta = -\dfrac{1}{2}i \{t - (1/t)\},\\ \cos^{2} \zeta + \sin^{2} \zeta = \dfrac{1}{4}[\{t + (1/t)\}^{2} - \{t - (1/t)\}^{2}] = 1 \end{gathered} \qquad \text{(3)} \] が成り立つと分かる。
さらに \(\zeta + \zeta'\) の三角関数を \(\zeta\) と \(\zeta'\) の三角関数を使って表せば、初等三角法で成り立つのと同じ公式が得られる。\(\exp (i\zeta) = t\) および \(\exp (i\zeta') = t'\) とすれば \[ \begin{aligned} \cos (\zeta + \zeta') & = \dfrac{1}{2} \left(tt' + \frac{1}{tt'}\right) \\ & = \dfrac{1}{4} \left\{ \left(t + \frac{1}{t}\right) \left(t' + \frac{1}{t'}\right) + \left(t - \frac{1}{t}\right) \left(t' - \frac{1}{t'}\right)\right\}\\ & = \cos\zeta \cos\zeta' - \sin\zeta \sin\zeta' \end{aligned} \qquad \text{(4)} \] となり、同様に \[ \sin (\zeta + \zeta') = \sin\zeta \cos\zeta' + \cos\zeta \sin\zeta' \qquad \text{(5)} \] も示せる。特に \[ \cos(\zeta + \dfrac{1}{2}\pi) = -\sin\zeta,\quad \sin(\zeta + \dfrac{1}{2}\pi) = \cos\zeta \qquad \text{(6)} \] が成り立つ。
初等三角法でよく見る公式はどれも \(\text{(2)}\)–\(\text{(6)}\) の代数的な系となる。そういった関係は全て、この節で一般化した三角関数の定義においても成り立つ。
§229 一般化された双曲線関数
例 87.19 で実数 \(\zeta\) に対する \(\cosh \zeta\) と \(\sinh \zeta\) を次の等式で定義した: \[ \cosh\zeta = \dfrac{1}{2} \{\exp \zeta + \exp (-\zeta)\},\quad \sinh\zeta = \dfrac{1}{2} \{\exp \zeta - \exp (-\zeta)\} \qquad \text{(1)} \]
ここまでの知識を使えばこの定義を複素数変数に対して拡張できる。つまり \(\text{(1)}\) を実数および複素数の全ての \(\zeta\) に対する \(\cosh \zeta\) と \(\sinh \zeta\) の定義とする。次の関係は簡単に確認できるだろう: \[ \cos i\zeta = \cosh \zeta,\quad \sin i\zeta = i\sinh \zeta,\quad \cosh i\zeta = \cos \zeta,\quad \sinh i\zeta = i\sin \zeta \]
\(\cos 2\zeta = \cos^{2} \zeta - \sin^{2} \zeta\) といった初等的な三角関数の公式は \(\zeta\) が複素数でも正しい。よって \(\cos \zeta\) を \(\cos i\zeta\) として、\(\sin \zeta\) を \(\sin i\zeta\) として、\(\cos 2\zeta\) を \(\cos 2i\zeta\) とした式も正しい。言い換えると \(\cos \zeta\) を \(\cosh \zeta\) として、\(\sin \zeta\) を \(i \sinh \zeta\) として、\(\cos 2\zeta\) を \(\cosh 2\zeta\) とした \[ \cosh 2\zeta = \cosh^{2} \zeta + \sinh^{2} \zeta \] が成り立つ。同様の変換は任意の三角関数の恒等式に適用できる。例 87.21 で示した三角関数と双曲線関数の間の対応関係を説明するのはこの事実である。
§230 \(\cos(ξ + iη)\) や \(\sin(ξ + iη)\) に関する公式
加法定理から \[ \begin{alignedat}{4} \cos (\xi + i\eta) & = \cos\xi \cos i\eta & & - \sin\xi \sin i\eta & & = \cos\xi \cosh \eta & & - i\sin\xi \sinh \eta,\\ \sin (\xi + i\eta) & = \sin\xi \cos i\eta & & + \cos\xi \sin i\eta & & = \sin\xi \cosh \eta & & + i\cos\xi \sinh \eta \end{alignedat} \] が分かる。この等式は全ての \(\xi\) と \(\eta\) に関して成り立つ。興味深いのは \(\xi\) と \(\eta\) が実数の場合で、このとき複素数に対する三角関数の実部と虚部を示す公式が得られる。
-
\(\cos\zeta\) と \(\sin\zeta\) が実数あるいは純虚数となる \(\zeta\) の値を求めよ。 [例えば \(\cos \zeta\) が実数になるのは \(\eta = 0\) または \(\xi\) が \(\pi\) の倍数のときである]
-
次が成り立つ: \[ \begin{alignedat}{2} \left|\cos (\xi + i\eta) \right| & = \sqrt{\cos^{2} \xi + \sinh^{2} \eta} & & = \sqrt{\dfrac{1}{2} (\cosh 2\eta + \cos 2\xi)}, \\ \left|\sin (\xi + i\eta) \right| & = \sqrt{\sin^{2} \xi + \sinh^{2} \eta} & & = \sqrt{\dfrac{1}{2} (\cosh 2\eta - \cos 2\xi)} \end{alignedat} \] [等式 \(\left|\cos(\xi + i\eta)\right| = \sqrt{\cos(\xi + i\eta) \cos(\xi - i\eta)}\) などを使う]
-
次が成り立つ: \[ \tan (\xi + i \eta) = \dfrac{\sin 2\xi + i\sinh 2\eta}{\cosh 2\eta + \cos 2\xi},\quad \cot (\xi + i \eta) = \dfrac{\sin 2\xi - i\sinh 2\eta}{\cosh 2\eta - \cos 2\xi} \]
[例えば \[ \tan (\xi + i\eta) = \frac{\sin (\xi + i\eta) \cos (\xi - i\eta)} {\cos (\xi + i\eta) \cos (\xi - i\eta)} = \frac{\sin 2\xi + \sin 2i\eta}{\cos 2\xi + \cos 2i\eta} \] を使えば結果が直ちに得られる]
-
次が成り立つ: \[ \begin{aligned} \sec (\xi + i \eta) & = \frac{\cos\xi \cosh\eta + i\sin\xi \sinh\eta} {\frac{1}{2} (\cosh 2\eta + \cos 2\xi)}, \\ \cosec (\xi + i \eta) & = \frac{\sin\xi \cosh\eta - i\cos\xi \sinh\eta} {\frac{1}{2} (\cosh 2\eta - \cos 2\xi)} \end{aligned} \]
-
\(|\cos (\xi + i\eta)| = 1\) なら \(\sin^{2} \xi = \sinh^{2} \eta\) が成り立つ。また \(|\sin (\xi + i\eta)| = 1\) なら \(\cos^{2} \xi = \sinh^{2} \eta\) が成り立つ。
-
\(|\cos (\xi + i\eta)| = 1\) なら次が成り立つ: \[ \sin \{\arg \cos (\xi + i\eta)\} = ±\sin^{2} \xi = ±\sinh^{2} \eta \]
-
\(\operatorname{Log} \cos (\xi + i\eta) = A + iB\) を示せ。ここで \[ A = \dfrac{1}{2} \log \{\dfrac{1}{2} (\cosh 2\eta + \cos 2\xi)\} \] であり、\(B\) は次の条件を満たすとする: \[ \frac{\cos B}{\cos\xi \cosh\eta} = -\frac{\sin B}{\sin\xi \sinh\eta} = \frac{1}{\sqrt{\frac{1}{2} (\cosh 2\eta + \cos 2\xi)}} \] \(\operatorname{Log} \sin (\xi + i\eta)\) に対する同様の等式を求めよ。
-
方程式 \(\bm{\cos \zeta = a}\) (\(\bm{a}\) は実数): \(\zeta = \xi + i\eta\) として実部と虚部をそれぞれ比較すれば次を得る: \[ \cos\xi \cosh\eta = a,\quad \sin\xi \sinh\eta = 0 \] よって \(\eta = 0\) または \(\xi\) が \(\pi\) の倍数となる。\(\eta = 0\) なら \(\cos \xi = a\) だから、\(-1 \leq a \leq 1\) のときに限って解 \[ \zeta = 2k\pi ± \arccos a \] を得る。ここで \(\arccos a\) は \(0\) から \(\frac{1}{2}\pi\) の値を取るとする。\(\xi = m\pi\) なら \(\cosh\eta = (-1)^{m}a\) だから、\(a \geq 1\) で \(m\) が偶数か、\(a \leq -1\) で \(m\) が奇数かである。\(a = ± 1\) なら \(\eta = 0\) となって一つ目の場合に帰着される。\(|a| \gt 1\) なら \(\cosh \eta = |a|\) であり、解は \[ \begin{alignedat}{4} \zeta & =& 2k & \pi ± i\log \{ & & a + \sqrt{a^{2} - 1}\}\quad & & (a \gt 1), \\ \zeta & =& (2k + 1) & \pi ± i\log \{-& & a + \sqrt{a^{2} - 1}\}\quad & & (a \lt -1) \end{alignedat} \] となる。例えば \(\cos\zeta = -\frac{5}{3}\) の解は \(\zeta = (2k + 1)\pi ± i\log 3\) となる。
-
方程式 \(\sin\zeta = \alpha\) を解け。\(\alpha\) は実数とする。
-
方程式 \(\bm{\cos\zeta = \alpha + i\beta}\) (\(\bm{\beta \neq 0}\)): \(\beta \lt 0\) に対する結果は \(i\) の符号を変えれば得られるので、\(\beta \gt 0\) の場合だけを考えればよい。すると \[ \cos\xi \cosh\eta = \alpha,\quad \sin\xi \sinh\eta = -\beta \qquad \text{(1)} \] であり、ここから次が分かる: \[ (\alpha/\cosh\eta)^{2} + (\beta/\sinh\eta)^{2} = 1 \]
\(\cosh^{2} \eta = x\) とすれば \[ x^{2} - (1 + \alpha^{2} + \beta^{2})x + \alpha^{2} = 0 \] が成り立つから、 \[ A_{1} = \dfrac{1}{2}\sqrt{(\alpha + 1)^{2} + \beta^{2}},\quad A_{2} = \dfrac{1}{2}\sqrt{(\alpha - 1)^{2} + \beta^{2}} \] とすれば \(x = (A_{1} ± A_{2})^{2}\) を得る。\(\alpha \gt 0\) と仮定する。このとき \(A_{1} \gt A_{2} \gt 0\) および \(\cosh\eta = A_{1} ± A_{2}\) だから \[ \cos\xi = \alpha/(\cosh\eta) = A_{1} \mp A_{2} \] が成り立つ。加えて \(\cosh\eta \gt \cos\xi\) だから \[ \cosh\eta = A_{1} + A_{2},\quad \cos\xi = A_{1} - A_{2} \] が分かる。この方程式の一般解は \[ \xi = 2k\pi ± \arccos M,\quad \eta = ±\log \{L + \sqrt{L^{2} - 1}\} \qquad \text{(2)} \] である。ここで \(L = A_{1} + A_{2},\ M = A_{1} - A_{2}\) で、\(\arccos M\) は \(0\) と \(\frac{1}{2}\pi\) の間とする。
しかしこうして求まる \(\eta\) と \(\xi\) の式は、方程式 \(\text{(1)}\) の解だけではなく \[ \cos\xi \cosh\eta = \alpha,\quad \sin\xi \sinh\eta = \beta \qquad \text{(3)} \] の解も表している。二乗した後の式しか使っていないためである。二つの解を区別するには、\(\sin \xi\) の符号が \(\text{(2)}\) の一つ目の式にある曖昧な符号と同じで、\(\sinh\eta\) の符号が二つ目の式の曖昧な符号と同じなことを利用する。\(\beta \gt 0\) だから、この二つの符号は異なる。よって一般解は \[ \zeta = 2k\pi ± [\arccos M - i\log \{L + \sqrt{L^{2} - 1}\}] \] となる。
-
\(\alpha \lt 0\) および \(\alpha = 0\) の場合を同様に解け。
-
\(\beta = 0\) なら \(L = \frac{1}{2}|\alpha + 1| + \frac{1}{2}|\alpha - 1|\) および \(M = \frac{1}{2}|\alpha + 1| - \frac{1}{2}|\alpha - 1|\) が成り立つ。この結果が問題 8 と矛盾しないことを示せ。
-
\(\alpha\) と \(\beta\) が両方とも正のとき、\(\sin\zeta = \alpha + i\beta\) の一般解が \[ \zeta = k\pi +(-1)^{k} [\arcsin M + i\log \{L + \sqrt{L^{2} - 1}\}] \] だと示せ。\(\arcsin M\) は \(0\) と \(\frac{1}{2}\pi\) の間の値を取るとする。他の可能な場合についても解を求めよ。
-
\(\tan \zeta = \alpha\) を解け。\(\alpha\) は実数とする。 [全ての根は実数である]
-
\(\beta \neq 0\) とする。\(\tan \zeta = \alpha + i\beta\) の一般解が \[ \zeta = k\pi + \dfrac{1}{2}\theta + \dfrac{1}{4} i\log\left\{ \frac{\alpha^{2} + (1 + \beta)^{2}} {\alpha^{2} + (1 - \beta)^{2}} \right\} \] だと示せ。\(\theta\) は次の等式を満たす絶対値が最小の角度とする: \[ \cos \theta : \sin \theta : 1 = 1 - \alpha^{2} - \beta^{2} : 2\alpha : \sqrt{(1 - \alpha^{2} - \beta^{2})^{2} + 4\alpha^{2}} \]
-
\(\xi\) と \(c\) を実数とする。\(z = \xi\exp(\frac{1}{4}\pi i)\) のとき \(\cos 2\pi z - \cos 2\pi c\) の絶対値が \[ \begin{aligned} \surd[\dfrac{1}{2}\{1 + \cos 4\pi c + \cos(2\pi\xi\sqrt{2}) & + \cosh(2\pi\xi\sqrt{2}) \\ & - 4\cos 2\pi c \cos(\pi\xi\sqrt{2}) \cosh(\pi\xi\sqrt{2})\}] \end{aligned} \] だと示せ。
-
次を示せ: \[ \begin{aligned} |\exp \exp(\xi + i\eta)| &= \exp(\exp\xi \cos\eta), \\ \operatorname{Re} \{\cos\cos(\xi + i\eta)\} & = \cos(\cos\xi \cosh\eta) \cosh(\sin\xi \sinh\eta),\\ \operatorname{Im} \{\sin\sin(\xi + i\eta)\} & = \cos(\sin\xi \cosh\eta) \sinh(\cos\xi \sinh\eta) \end{aligned} \]
-
原点を通る直線で \(x\) 軸正方向との角度が \(\frac{1}{2}\pi\) 以下のものを考える。この直線上を \(\zeta\) が無限遠に向かって進むとき、\(|\exp \zeta|\) が \(\infty\) に向かうと示せ。また \(x\) 軸正方向との角度が \(\frac{1}{2}\pi\) 以上なら同じ式が \(0\) に向かうと示せ。
-
原点を通る実軸でない任意の直線上を \(\zeta\) が無限遠に向かって進むとき、 \(|\cos \zeta|\) と \(|\sin \zeta|\) が \(\infty\) に向かうと示せ。
-
問題 19 の直線上を \(\zeta\) が無限遠に向かって進むとき、\(\tan \zeta\) は \(-i\) あるいは \(i\) に向かうと示せ。たどる直線が実軸の上方にあるなら \(-i\) に向かい、実軸の下方にあるなら \(i\) に向かう。
§231 対数関数と逆三角関数の関係
第六章で見たように、定数 \(\alpha,\ \beta,\ \ldots\) を使った有理関数あるいは代数関数 \(\phi(x, \alpha, \beta,\ \ldots)\) の積分は \(\alpha,\ \beta,\ \ldots\) の値によって異なる形になる場合がある: 積分が対数関数で表されることもあれば、逆三角関数で表されることもある。例えば \(a \gt 0\) なら \[ \int \frac{dx}{x^{2} + \alpha} = \frac{1}{\sqrt{\alpha}} \arctan \frac{x}{\sqrt{\alpha}} \qquad \text{(1)} \] だが、\(\alpha \lt 0\) なら \[ \int \frac{dx}{x^{2} + \alpha} = \frac{1}{2\sqrt{-\alpha}} \log \left|\frac{x - \sqrt{-\alpha}}{x + \sqrt{-\alpha}}\right| \qquad \text{(2)} \] となる。この事実は対数関数と逆三角関数の間に何らかの関数的な関係があることを示唆する。あるいは三角関数を \(\exp i\zeta\) を使って表現でき、対数関数が指数関数の逆関数である事実からもこの関係の存在が導けるだろう。
さらに具体的に \[ \int \frac{dx}{x^{2} - \alpha^{2}} = \frac{1}{2\alpha} \log \left(\frac{x - \alpha}{x + \alpha}\right) \] を考えよう。この等式は \(\alpha\) が実数で \((x - \alpha)/(x + \alpha)\) が正のとき成り立つ。この等式に含まれる \(\alpha\) に \(i\alpha\) を無理やり代入すると、定数 \(C\) が混じった等式 \[ \arctan \left(\frac{x}{\alpha}\right) = \frac{1}{2i} \log\left(\frac{x - i\alpha}{x + i\alpha}\right) + C \qquad \text{(3)} \] が得られる。この章で複素数に対する対数関数を定義したので、この等式が本当に正しいのかという問題を考えることができる。
§221 から \[ \operatorname{Log}(x ± i\alpha) = \dfrac{1}{2} \log(x^{2} + \alpha^{2}) ± i(\phi + 2k\pi) \] が分かる。ここで \(k\) は整数で、\(\phi\) は \(\cos\phi = x/\sqrt{x^{2} + \alpha^{2}}\) と \(\sin\phi = \alpha/\sqrt{x^{2} + \alpha^{2}}\) を満たす最小の角度である。ここから \[ \frac{1}{2i} \operatorname{Log}\left(\frac{x - i\alpha}{x + i\alpha}\right) = -\phi - l\pi \] が整数 \(l\) に対して成り立つと分かる。確かにこれは \(\arctan(x/\alpha)\) の任意の値から定数しか離れていない。
対数関数と逆三角関数を結ぶ標準的な等式を次に示す: \[ \arctan x = \frac{1}{2i} \operatorname{Log}\left(\frac{1 + ix}{1 - ix}\right) \qquad \text{(4)} \] ここで \(x\) は実数を表す。これを確認するには \(x = \tan y\) とするのが一番簡単であり、このとき右辺は \[ \frac{1}{2i} \operatorname{Log}\left(\frac{\cos y + i\sin y}{\cos y - i\sin y}\right) = \frac{1}{2i} \operatorname{Log}(\exp 2iy) = y + k\pi \] となる (\(k\) は任意の整数)。ここから等式 \(\text{(4)}\) は "完全に" 正しいと分かる (例 93.3)。また \(-1 \leq x \leq 1\) に対する \[ \begin{gathered} \arccos x = -i \operatorname{Log}\{x ± i\sqrt{1 - x^{2}}\},\\ \arcsin x = -i \operatorname{Log}\{ix ± \sqrt{1 - x^{2}}\} \end{gathered} \qquad \text{(5)} \] も確認できるはずである。これらの等式も "完全に" 正しい。
\(y = \exp(iu)\) に対する方程式 \[ \cos u = x = \dfrac{1}{2}\{y + (1/y)\} \] を \(y\) について解くと \(y = x ± i\sqrt{1 - x^{2}}\) を得る。よって \[ u = -i \operatorname{Log} y = -i \operatorname{Log}\{x ± i\sqrt{1 - x^{2}}\} \] が成り立つ。これは \(\text{(5)}\) の一つ目の等式に等しい。\(\text{(5)}\) の二つ目の等式と \(\text{(4)}\) を同様の議論によって導け。
§232 \(\exp z\) のべき級数
§212 で見たように、\(z\) が実数なら2 \[ \exp z = 1 + z +\frac{z^{2}}{2!} + \cdots \qquad \text{(1)} \] が成り立つ。さらに §191 からは、\(z\) が複素数のときにも右辺の級数が収束する (実際には絶対収束する)ことが分かる。よって複素数の \(z\) に対しても \(\text{(1)}\) が正しいことが自然に予想される。これを示そう。
\(\text{(1)}\) の級数の和を \(F(z)\) とする。級数は絶対収束するから、級数の積 (例 81.7) を直接考えることで、\(F(z)\) が次の関数方程式を満たすことが分かる: \[ F(z) F(h) = F(z + h) \qquad \text{(2)} \] 実数 \(y\) を使って \(z = iy\) および \(F(z) = f(y)\) とすれば \[ f(y) f(k) = f(y + k) \] だから、 \[ \frac{f(y + k) - f(y)}{k} = f(y) \left\{\frac{f(k) - 1}{k}\right\} \] が成り立つ。
一方で \[ \frac{f(k) - 1}{k} = i\left\{1 + \frac{ik}{2!} + \frac{(ik)^{2}}{3!} + \cdots\right\} \] より、\(|k| \lt 1\) で \[ \left|\frac{f(k) - 1}{k} - i\right| \lt \left(\frac{1}{2!} + \frac{1}{3!} + \cdots\right)|k| \lt (e - 2)|k| \] が成り立つ。よって \(k \to 0\) で \(\{f(k) - 1\}/k\to i\) であり、 \[ f'(y) = \lim_{k \to 0} \frac{f(y + k) - f(y)}{k} = if(y) \qquad \text{(3)} \] を得る。
よって \[ f(y) = F(iy) = 1 + (iy) + \frac{(iy)^{2}}{2!} + \cdots = \phi(y) + i\psi(y) \] とすれば、\(\phi(y)\) は偶関数で \(\psi(y)\) は奇関数となる。この \(\phi(y)\) と \(\psi(y)\) に対して \[ \begin{aligned} |f(y)| & = \sqrt{\{\phi(y)\}^{2} + \{\psi(y)\}^{2}}\\ & = \sqrt{\{\phi(y) + i\psi(y)\}\{\phi(y) - i\psi(y)\}}\\ & = \sqrt{F(iy) F(-iy)} = \sqrt{F(0)} = 1 \end{aligned} \] が成り立つ。したがって \[ f(y) = \cos Y + i \sin Y \] とすれば \(Y\) は \(-\pi \lt Y \leq \pi\) を満たす \(y\) の関数となる。\(f(y)\) は微分係数を持つから、その実部および虚部 \(\cos Y\) と \(\sin Y\) も微分係数を持つ。よって \(Y\) は \(y\) の連続関数と分かる。\(y\) が \(y + k\) まで変化するとき \(Y\) が \(Y + K\) に変化するとすれば、\(K\) は \(k\) と共に \(0\) に向かう。そして \[ \frac{K}{k} = \biggl\{\frac{\cos(Y + K) - \cos Y}{k}\biggr\} \bigg/ \biggl\{\frac{\cos(Y + K) - \cos Y}{K}\biggr\} \] が成り立つ。\(\cos Y\) は \(y\) で微分できるから、右辺の分数の分母は \(k \to 0\) で極限を持つ。また分子は \(-\sin Y\) という極限を持つ。よって \(K/k\) は極限に向かい、\(Y\) は \(y\) で微分できる。
よって \[ f'(y) = (-\sin Y + i\cos Y) \frac{dY}{dy} \] が成り立つ。一方既に示したように \[ f'(y) = if(y) = -\sin Y + i\cos Y \] だから、定数 \(C\) を使って \[ \frac{dY}{dy} = 1,\quad Y = y + C \] つまり \[ f(y) = \cos(y + C) + i\sin(y + C) \] と書ける。
ここで \(y = 0\) で \(f(0) = 1\) より \(C\) は \(2\pi\) の倍数で \(f(y) = \cos y + i\sin y\) だと分かる。したがって全ての実数 \(y\) で \(F(iy) = \cos y + i\sin y\) であり、\(x\) を実数とすれば \[ F(x + iy) = F(x) F(iy) = \exp x(\cos y + i\sin y) = \exp(x + iy) \] が成り立つ。つまり \[ \exp z = 1 + z + \frac{z^{2}}{2!} + \cdots \] が全ての \(z\) に対して成り立つ。
§233 \(\cos z\) と \(\sin z\) のべき級数展開
前節の結果と §228 の等式 \(\text{(1)}\) から、全ての \(z\) に対する等式 \[ \cos z = 1 - \frac{z^{2}}{2!} + \frac{z^{4}}{4!} - \cdots,\quad \sin z = z - \frac{z^{3}}{3!} + \frac{z^{5}}{5!} - \cdots \] を得る。実数 \(z\) に対するこの結果は 例 56.1 で示した。
-
\(\cos z\) と \(\sin z\) のべき級数を使って \(\cos i\) と \(\sin i\) を小数点以下第二位まで計算せよ。
-
\(|\cos z| \leq \cosh|z|\) と \(|\sin z| \leq \sinh|z|\) を示せ。
-
\(|z| \lt 1\) なら \(|\cos z| \lt 2\) および \(|\sin z| \lt \dfrac{6}{5}|z|\) だと示せ。
-
\(\sin 2z = 2\sin z \cos z\) から \[ (2z) - \frac{(2z)^{3}}{3!} + \frac{(2z)^{5}}{5!} - \cdots = 2\left(z - \frac{z^{3}}{3!} + \cdots\right) \left(1 - \frac{z^{2}}{2!} + \cdots\right) \] が分かる。右辺の二つの級数の積 (§195) を計算し、係数を比較 (§194) することで \[ \binom{2n + 1}{1} + \binom{2n + 1}{3} + \cdots + \binom{2n + 1}{2n + 1} = 2^{2n} \] を得る。この結果を二項定理を使って確認せよ。同様の恒等式を次の等式から導け: \[ \cos^{2}z + \sin^{2}z = 1,\quad \cos2z = 2\cos^{2}z - 1 = 1 - 2\sin^{2}z \]
-
次を示せ: \[ \exp\{(1 + i)z\} = \sum_{0}^{\infty} 2^{\frac{1}{2}n} \exp(\dfrac{1}{4}n\pi i) \frac{z^{n}}{n!} \]
-
\(\cos z \cosh z\) を \(z\) のべき級数に展開せよ。 [等式 \[ \begin{aligned} \cos z \cosh z + i\sin z \sinh z & = \cos\{(1 - i)z\}\\ & = \dfrac{1}{2} [\exp\{(1 + i)z\} + \exp\{-(1 + i)z\}]\\ & = \dfrac{1}{2} \sum_{0}^{\infty} 2^{\frac{1}{2}n} \{1 + (-1)^{n}\} \exp(\dfrac{1}{4}n\pi i) \frac{z^{n}}{n!} \end{aligned} \] および \[ \begin{aligned} \cos z \cosh z - i\sin z \sinh z & = \cos (1 + i)z \\ & = \dfrac{1}{2} \sum_{0}^{\infty} 2^{\frac{1}{2}n} \{1 + (-1)^{n}\} \exp(-\dfrac{1}{4}n\pi i) \frac{z^{n}}{n!} \end{aligned} \] から \[ \begin{aligned} \cos z \cosh z & = \dfrac{1}{2} \sum_{0}^{\infty} 2^{\frac{1}{2}n}\{1 + (-1)^{n}\} \cos \dfrac{1}{4}n\pi \frac{z^{n}}{n!} \\ & = 1 - \frac{2^{2}z^{4}}{4!} + \frac{2^{4}z^{8}}{8!} - \cdots \end{aligned} \] が分かる]
-
\(\sin z \sinh z,\ \cos z \sinh z,\ \sin z \cosh z\) を \(z\) のべき級数に展開せよ。
-
\(\sin^{2} z\) と \(\sin^{3} z\) を \(z\) のべき級数に展開せよ。 [等式 \[ \sin^{2} z = \dfrac{1}{2} (1 - \cos 2z),\quad \sin^{3} z = \dfrac{1}{4} (3\sin z - \sin 3z),\ \cdots \] を使う。任意の整数 \(n\) に対する \(\cos^{n} z\) と \(\sin^{n} z\) も同じ方法で展開できる]
-
級数 \[ C = 1 + \frac{\cos z}{1!} + \frac{\cos 2z}{2!} + \frac{\cos 3z}{3!} +\cdots,\quad S = \frac{\sin z}{1!} + \frac{\sin 2z}{2!} + \frac{\sin 3z}{3!} + \cdots \] の和を求めよ。
[ここでは \[ \begin{aligned} C + iS & = 1 + \dfrac{\exp(iz)}{1!} + \dfrac{\exp(2iz)}{2!} + \cdots \\ & = \exp\{\exp(iz)\} = \exp(\cos z) \{\cos(\sin z) + i\sin(\sin z)\} \end{aligned} \] および同様に \[ C - iS = \exp\{\exp(-iz)\} = \exp(\cos z)\{\cos(\sin z) - i\sin(\sin z)\} \] だから、 \[ C = \exp(\cos z)\cos(\sin z),\quad S = \exp(\cos z)\sin(\sin z) \] が分かる]
-
級数 \[ 1 + \frac{a\cos z}{1!} + \frac{a^{2}\cos 2z}{2!} + \cdots,\quad \frac{a\sin z}{1!} + \frac{a^{2}\sin 2z}{2!} + \cdots \] の和を求めよ。
-
級数 \[ 1 - \frac{\cos 2z}{2!} + \frac{\cos 4z}{4!} - \cdots,\quad \frac{\cos z}{1!} - \frac{\cos 3z}{3!} + \cdots \] の和を求め、サインを使った同様の級数の和を求めよ。
-
次を示せ: \[ 1 + \frac{\cos 4z}{4!} + \frac{\cos 8z}{8!} + \cdots = \dfrac{1}{2}\{\cos(\cos z) \cosh(\sin z) + \cos(\sin z) \cosh(\cos z)\} \]
-
\(\cos(x + h)\) と \(\sin(x + h)\) の \(h\) のべき級数への展開 (例 56.1) が実数および複素数の全ての \(x\) と \(h\) で正しいことを示せ。
§234 対数級数 (その 1)
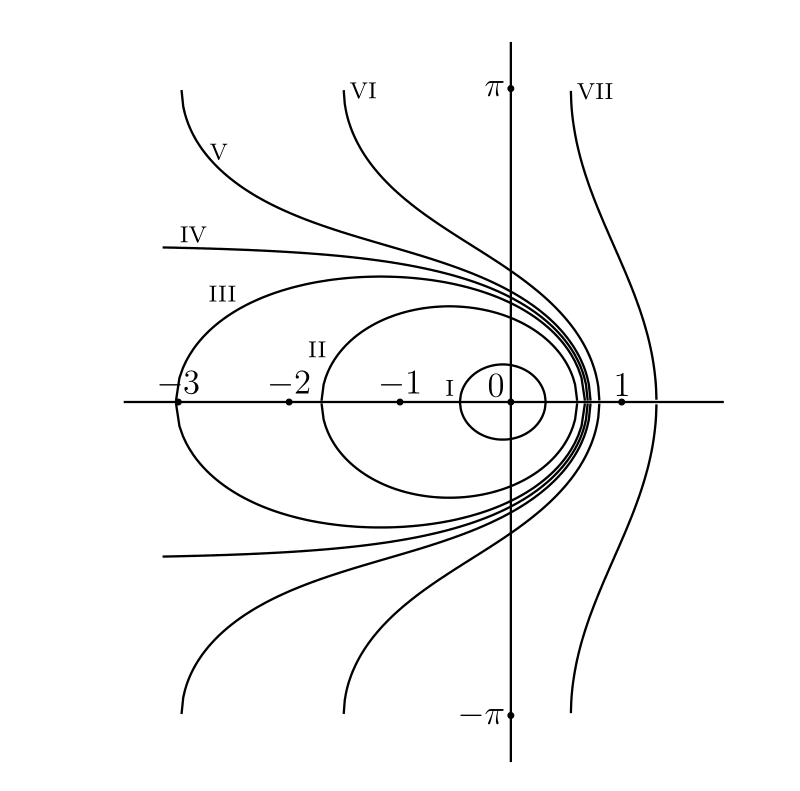
§213 では \[ \log(1 + z) = z - \dfrac{1}{2} z^{2} + \dfrac{1}{3} z^{3} - \cdots \qquad \text{(1)} \] が絶対値が \(1\) より小さい実数 \(z\) で成り立つことを見た。右辺の級数は \(z\) が絶対値が \(1\) より小さい複素数であっても収束し、その収束は絶対収束となる。ここから \(\text{(1)}\) がそういった複素数の \(z\) でも成り立つことが自然に予想されるが、実際それは §213 の議論を変えれば証明できる。これから示すのは、\(\text{(1)}\) が \(|z| \leq 1\) を満たす \(-1\) 以外の全ての \(z\) で成り立つというより強い命題である。
前に定義したように \(\log(1 + z)\) は \(\operatorname{Log}(1 + z)\) の主値であり、複素変数 \(u\) の平面上の点 \(1\) と \(1 + z\) を結ぶ直線 \(C\) に対する \[ \log(1 + z) = \int_{C} \frac{du}{u} \] が定義である。実数変数 \(z\) 対する \(\text{(1)}\) は前に示したので、これから \(z\) は実数でないと仮定する。
ここで \[ z = r(\cos\theta + i\sin\theta) = \zeta r \] とすれば \(|r| \leq 1\) であり、 \[ u = 1 + \zeta t \] とすれば \(t\) が \(0\) から \(r\) まで \(u\) は \(C\) 上を動く。そして \[ \begin{aligned} \int_{C} \frac{du}{u} & = \int_{0}^{r} \frac{\zeta\, dt}{1 + \zeta t} \\ & = \int_{0}^{r} \left\{\zeta - \zeta^{2} t + \zeta^{3} t^{2} - \cdots + (-1)^{m-1} \zeta^{m} t^{m-1} + \frac{(-1)^{m} \zeta^{m+1} t^{m}}{1 + \zeta t}\right\} dt \\ & = \zeta r - \frac{(\zeta r)^{2}}{2} + \frac{(\zeta r)^{3}}{3} - \cdots + (-1)^{m-1} \frac{(\zeta r)^{m}}{m} + R_{m} \\ & = z - \frac{z^{2}}{2} + \frac{z^{3}}{3} - \cdots + (-1)^{m-1} \frac{z^{m}}{m} + R_{m} \end{aligned} \qquad \text{(2)} \] が成り立つ。\(R_{m}\) は次の形をしている: \[ R_{m} = (-1)^{m} \zeta^{m+1} \int_{0}^{r} \frac{t^{m}\, dt}{1 + \zeta t} \qquad \text{(3)} \]
§164 の不等式 \(\text{(1)}\) から \[ |R_{m}| \leq \int_{0}^{r} \frac{t^{m}\, dt}{|1 + \zeta t|} \qquad \text{(4)} \] が分かる。また \(O\) から \(C\) に引いた垂線の長さを \(\varpi\) とすると、\(|1 + \zeta t|\) つまり \(u\) は \(\varpi\) 以下となる3。ここから \[ |R_{m}| \leq \frac{1}{\varpi} \int_{0}^{r} t^{m}\, dt = \frac{r^{m+1}}{(m + 1) \varpi} \leq \frac{1}{(m + 1) \varpi} \] を得る。よって \(m \to \infty\) で \(R_{m} \to 0\) であり、\(\text{(2)}\) から \[ \log(1 + z) = z - \dfrac{1}{2} z^{2} + \dfrac{1}{3} z^{3} - \cdots \qquad \text{(5)} \] が分かる。
もちろんこの証明は級数の収束を仮定しているが、これは前に示した (例 80.4)。この級数は \(|z| \lt 1\) なら絶対収束し、\(|z| = 1\) なら条件収束する。
また \(z\) を \(-z\) に変えると \[ \log \left(\frac{1}{1 - z}\right) = -\log(1 - z) = z + \dfrac{1}{2} z^{2} + \dfrac{1}{3} z^{3} + \cdots \qquad \text{(6)} \] を得る。
§235 対数級数 (その 2)
ここまでの議論から次の等式が分かる: \[ \begin{aligned} \log(1 + z) & = \log\{(1 + r \cos\theta) + ir\sin\theta\} \\ & = \dfrac{1}{2} \log(1 + 2r\cos\theta + r^{2}) + i\arctan \left(\frac{r\sin\theta}{1 + r\cos\theta}\right) \end{aligned} \]
この等式におけるタンジェントの逆関数は \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) の値を取らなければならない。\(1 + z\) が \(-1\) から \(z\) への直線で表されるので、円 \(|z| = 1\) の内部にある \(z\) に対しては \(\arg(1 + z)\) の主値は常にこの範囲にある。
\(z^{m} = r^{m}(\cos m\theta + i\sin m\theta)\) だから、§234 の等式 \(\text{(5)}\) と実部と虚部をそれぞれ比較して \[ \begin{aligned} \dfrac{1}{2} \log(1 + 2r\cos\theta + r^{2}) & = r\cos\theta - \dfrac{1}{2}r^{2} \cos 2\theta + \dfrac{1}{3}r^{3} \cos 3\theta - \cdots, \\ \arctan \left(\frac{r\sin\theta}{1 + r\cos\theta}\right) & = r\sin\theta - \dfrac{1}{2}r^{2} \sin 2\theta + \dfrac{1}{3}r^{3} \sin 3\theta - \cdots \end{aligned} \] を得る。この二つの等式は \(0 \leq r \leq 1\) で全ての \(\theta\) に対して成り立つが、唯一の例外として \(r = 1\) のときは \(\theta\) が \(\pi\) の倍数であってはならない。
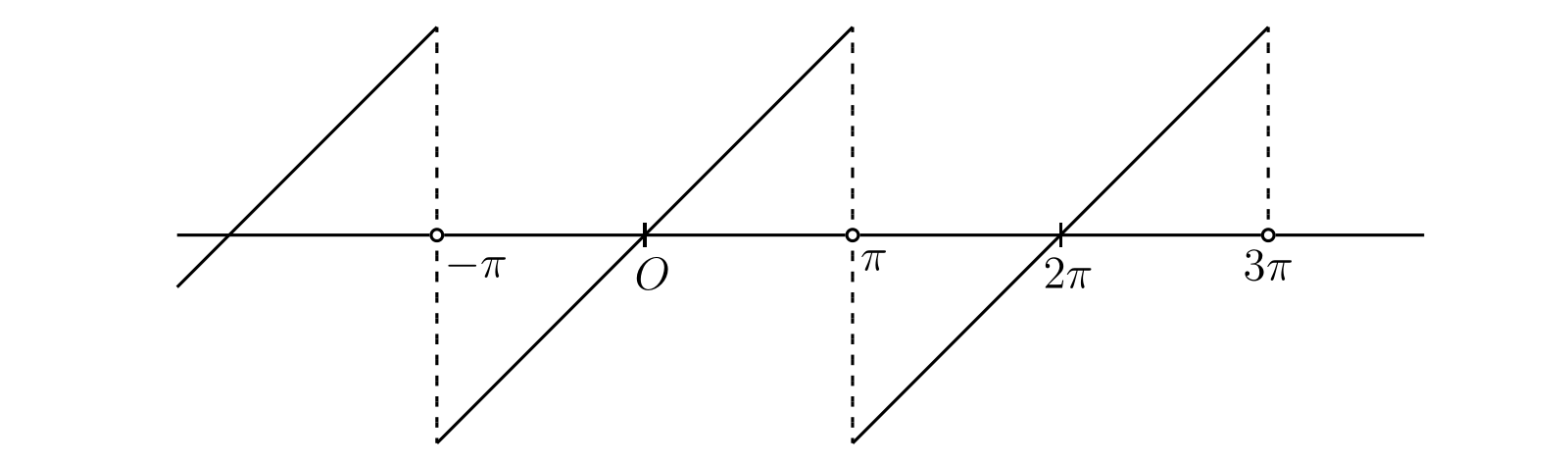
特に興味深いのが \(r = 1\) の場合で、このとき \(-\pi \lt \theta \lt \pi\) で \[ \begin{aligned} \log(1 + z) & = \log(1 + \operatorname{Cis}\theta) \\ & = \dfrac{1}{2} \log(2 + 2\cos\theta) + i\arctan\left(\frac{\sin\theta}{1 + \cos\theta}\right) \\ & = \dfrac{1}{2} \log(4\cos^{2} \dfrac{1}{2}\theta) + \dfrac{1}{2}i\theta \end{aligned} \] が成り立つ。つまり \[ \begin{alignedat}{4} \cos\theta & - \dfrac{1}{2} \cos 2\theta & & + \dfrac{1}{3} \cos 3\theta & & - \cdots & & = \dfrac{1}{2} \log(4\cos^{2} \dfrac{1}{2}\theta), \\ \sin\theta & - \dfrac{1}{2} \sin 2\theta & & + \dfrac{1}{3} \sin 3\theta & & - \cdots & & = \dfrac{1}{2} \theta \end{alignedat} \] である。他の \(\theta\) に対する級数の和を計算するには、二つの級数が \(\theta\) に関する周期 \(2\pi\) の周期関数である事実を使う。するとコサインの級数の和は \(\theta\) が \(\pi\) の奇数倍となる (級数が発散する) 場合を除いた全ての \(\theta\) で \(\frac{1}{2} \log(4\cos^{2} \frac{1}{2}\theta)\) となり、サインの級数の和は \((2k - 1)\pi \lt \theta \lt (2k + 1)\pi\) で \(\frac{1}{2} (\theta - 2k\pi)\) そして \(\theta\) が \(\pi\) の奇数倍なら \(0\) となることが分かる。このサイン級数が表す関数のグラフを 図 58 に示す。この関数は \(\theta = (2k + 1)\pi\) で不連続となる。
\(\text{(5)}\) の \(z\) を \(iz\) および \(-iz\) に書き換えて引くと \[ \frac{1}{2i} \log\left(\frac{1 + iz}{1 - iz}\right) = z - \dfrac{1}{3}z^{3} + \dfrac{1}{5}z^{5} - \cdots \] を得る。§231 の結果から、絶対値が \(1\) より小さい実数 \(z\) に対する \[ \arctan z = z - \dfrac{1}{3}z^{3} + \dfrac{1}{5}z^{5} - \cdots \] が導かれる。これは §214 で異なる方法を使って示した公式である。
-
\(a \gt b\) が成り立つ任意の三角形で \[ \log c = \log a - \frac{b}{a} \cos C - \frac{b^{2}}{2a^{2}} \cos 2C - \cdots \] だと示せ。[等式 \(\log c = \frac{1}{2} \log(a^{2} + b^{2} - 2ab\cos C )\) を使う]
-
\(-1 \lt r \lt 1\) かつ \(-\frac{1}{2}\pi \lt \theta \lt \frac{1}{2}\pi\) なら \[ r\sin 2\theta - \dfrac{1}{2}r^{2} \sin 4\theta + \dfrac{1}{3}r^{3} \sin 6\theta - \cdots = \theta - \arctan \left\{\left(\frac{1 - r}{1 + r}\right) \tan\theta\right\} \] だと示せ。タンジェントの逆関数は \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) の値を取るとする。任意の \(\theta\) に対する級数の和を計算せよ。
-
\(\log(1 + iz)\) と \(\log(1 - iz)\) を \(z\) のべき級数へ展開することで、\(-1 \lt r \lt 1\) に対する \[ \begin{gathered} \begin{alignedat}{4} r\sin\theta & + \dfrac{1}{2}r^{2} \cos 2\theta & & - \dfrac{1}{3}r^{3} \sin 3\theta & & - \dfrac{1}{4}r^{4} \cos 4\theta + \cdots & & = \dfrac{1}{2} \log(1 + 2r \sin\theta + r^{2}),\\ r\cos\theta & + \dfrac{1}{2}r^{2} \sin 2\theta & & - \dfrac{1}{3}r^{3} \cos 3\theta & & - \dfrac{1}{4}r^{4} \sin 4\theta + \cdots & & = \arctan \left(\frac{r\cos\theta}{1 - r\sin\theta}\right), \end{alignedat} \\ \begin{alignedat}{2} r\sin\theta & - \dfrac{1}{3}r^{3} \sin 3\theta + \cdots & & = \dfrac{1}{4} \log\left(\frac{1 + 2r \sin\theta + r^{2}} {1 - 2r \sin\theta + r^{2}}\right),\\ r\cos\theta & - \dfrac{1}{3}r^{3} \cos 3\theta + \cdots & & = \dfrac{1}{2} \arctan \left(\frac{2r\cos\theta}{1 - r^{2}}\right) \end{alignedat} \end{gathered} \] を示せ。タンジェントの逆関数は \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) の値を取るとする。
-
次を示せ: \[ \begin{alignedat}{3} \cos\theta \cos\theta & - \dfrac{1}{2} \cos 2\theta \cos^{2}\theta & & + \dfrac{1}{3} \cos 3\theta \cos^{3} \theta - \cdots & & = \dfrac{1}{2} \log(1 + 3\cos^{2} \theta),\\ \sin\theta \sin\theta & - \dfrac{1}{2} \sin 2\theta \sin^{2}\theta & & + \dfrac{1}{3} \sin 3\theta \sin^{3} \theta - \cdots & & = \operatorname{arccot} (1 + \cot\theta + \cot^{2}\theta) \end{alignedat} \] タンジェントの逆関数は \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) の値を取るとする。次の級数の和に対する同様の表現を求めよ: \[ \cos\theta \sin\theta - \dfrac{1}{2} \cos 2\theta \sin^{2}\theta + \cdots,\quad \sin\theta \cos\theta - \dfrac{1}{2} \sin 2\theta \cos^{2}\theta + \cdots \]
§236 対数級数の指数極限への応用
\(z\) を任意の複素数、\(h\) を十分小さな実数として、\(|hz| \lt 1\) が成り立つとする。このとき \[ \log(1 + hz) = hz - \dfrac{1}{2}(hz)^{2} + \dfrac{1}{3}(hz)^{3} - \cdots \] であり、 \[ \frac{\log(1 + hz)}{h} = z + \phi(h, z) \] とすれば \[ \begin{gathered} \phi(h, z) = -\dfrac{1}{2}hz^{2} + \dfrac{1}{3}h^{2}z^{3} - \dfrac{1}{4}h^{3}z^{4} + \cdots,\\ |\phi(h, z)| \lt |hz^{2}| (1 + |hz| + |h^{2}z^{2}| + \cdots) = \frac{|hz^{2}|}{1 - |hz|} \end{gathered} \] が分かる。\(h \to 0\) で \(\phi(h, z) \to 0\) だから、次が成り立つ: \[ \lim_{h\to 0} \frac{\log(1 + hz)}{h} = z \qquad \text{(1)} \]
特に正の整数 \(n\) を使って \(h = 1/n\) と書けば \[ \lim_{n\to \infty} n\log \left(1 + \frac{z}{n}\right) = z \] を得る。よって \[ \lim_{n\to \infty} \left(1 + \frac{z}{n}\right)^{n} = \lim_{n\to \infty} \exp\left\{n\log\left(1 + \frac{z}{n}\right)\right\} = \exp z \qquad \text{(2)} \] が成り立つ。これは §208 で実数 \(z\) に対して示した命題の一般化である。
\(\text{(1)}\) からは次節で必要になる他の結果も導ける。\(t\) と \(h\) を実数とすると、\(h\) が十分小さければ \[ \frac{\log(1 + tz + hz) - \log(1 + tz)}{h} = \frac{1}{h}\log\left(1 + \frac{hz}{1 + tz}\right) \] が成り立つ。これは \(h \to 0\) で極限 \(z/(1 + tz)\) に向かうので \[ \frac{d}{dt} \{\log(1 + tz)\} = \frac{z}{1 + tz} \qquad \text{(3)} \] を得る。
実数および複素数の任意の \(m\) に対する \((1 + tz)^{m}\) の \(t\) に関する微分の公式も必要になる。まず、実部が \(\phi(t)\) で虚部が \(\chi(t)\) の複素関数 \(\phi(t) = \psi(t) + i\chi(t)\) が導関数を持つなら \[ \begin{aligned} \frac{d}{dt}(\exp\phi) & = \frac{d}{dt}\{(\cos\chi + i\sin\chi) \exp\psi\}\\ & = \{(\cos\chi + i\sin\chi) \psi' + (-\sin\chi + i\cos\chi)\chi'\} \exp\psi\\ & = (\psi' + i\chi')(\cos\chi + i\sin\chi) \exp\psi\\ & = (\psi' + i\chi') \exp(\psi + i\chi) = \phi' \exp\phi \end{aligned} \] が成り立つ。つまり \(\exp \phi\) の微分規則は \(\phi\) が実関数の場合と変わらない。ここから \[ \begin{aligned} \frac{d}{dt}(1 + tz)^{m} & = \frac{d}{dt} \exp\{m\log(1 + tz)\}\\ & = \frac{mz}{1 + tz} \exp\{m\log(1 + tz)\}\\ & = mz(1 + tz)^{m-1} \end{aligned} \qquad \text{(4)} \] を得る。ここで \((1 + tz)^{m}\) と \((1 + tz)^{m-1}\) は主値とする。
§237 二項定理の一般形
§215 では級数 \[ 1 + \binom{m}{1} z + \binom{m}{2} z^{2} + \cdots \] の和が \((1 + z)^{m} = \exp\{m\log(1 + z)\}\) であり、全ての実数 \(m\) と \(-1\) から \(1\) の全ての実数 \(z\) で成り立つことを示した。\(a_{n}\) を \(z^{n}\) の係数とすれば \[ \left|\frac{a_{n+1}}{a_{n}}\right| = \left|\frac{m - n}{n + 1}\right| \to 1 \] が実数および複素数 \(m\) で成立する。よって (例 53.3 より) この級数は大きさが \(1\) より小さい任意 \(z\) で収束することが分かる。その和が \(\exp\{m\log(1 + z)\}\) つまり \((1 + z)^{m}\) の主値で変わらないことをこれから証明しよう。
§236 から実数 \(t\) に対して \[ \frac{d}{dt}(1 + tz)^{m} = mz(1 + tz)^{m-1} \] だと分かる。ここで \(z\) と \(m\) は任意の実数または複素数であり、両辺は主値を考える。よって \(\phi(t) = (1 + tz)^{m}\) とすれば \[ \phi^{(n)}(t) = m(m - 1) \cdots (m - n + 1)z^{n} (1 + tz)^{m-n} \] を得る。これは \(t = 0\) でも成り立つので \[ \frac{\phi^{n}(0)}{n!} = \binom{m}{n} z^{n} \] が分かる。
§164 の最後で指摘したように \[ \phi(1) = \phi(0) + \phi'(0) + \frac{\phi''(0)}{2!} + \cdots + \frac{\phi^{(n-1)}(0)}{(n - 1)!} + R_{n} \] が成り立つ。ここで \[ R_{n} = \frac{1}{(n - 1)!}\int_{0}^{1} (1 - t)^{n-1} \phi^{(n)}(t)\, dt \] である。一方 \(z = r(\cos\theta + i\sin\theta)\) なら \[ |1 + tz| = \sqrt{1 + 2tr\cos\theta + t^{2}r^{2}} \geq 1 - tr \] だから、\(0 \lt \theta \lt 1\) を満たす \(\theta\) に対して \[ \begin{aligned} |R_{n}| & \lt \frac{|m(m - 1) \cdots (m - n + 1)|}{(n - 1)!}\, r^{n} \int_{0}^{1} \frac{(1 - t)^{n-1}}{(1 - tr)^{n-m}}\, dt\\ & \lt \frac{|m(m - 1) \cdots (m - n + 1)|}{(n - 1)!}\, \frac{(1 - \theta)^{n-1} r^{n}}{(1 - \theta r)^{n-m}} \end{aligned} \] を得る。つまり \[ |R_{n}| \lt K\frac{|m(m - 1) \cdots (m - n + 1)|}{(n - 1)!}\, r^{n} = \rho_{n} \] とできる (参考: §163)。そして \[ \frac{\rho_{n+1}}{\rho_{n}} = \frac{|m - n|}{n}r \to r \] だから、(例 27.6 より) \(n \to \infty\) のとき \(\rho_{n} \to 0\) および \(R_{n} \to 0\) となる。ここから上述の結果が得られる。
二項級数 \[ 1 + \binom{m}{1} z + \binom{m}{2} z^{2} + \cdots \] の和は \(\exp\{m\log(1 + z)\}\) である。ここで対数は主値を考え、\(m\) は実数および複素数の任意の値であり、\(z\) は \(|z| \lt 1\) を満たすとする。
より難しい \(|z| = 1\) の場合を含む二項級数に関する完全な議論はブロムウィッチ著 Infinite Series pp. 225 et seq. にある。
-
\(m\) を実数とする。このとき \[ \log(1 + z) = \dfrac{1}{2} \log(1 + 2r\cos\theta + r^{2}) + i\arctan\left(\frac{r\sin\theta}{1 + r\cos\theta}\right) \] が成り立つから、 \[ \begin{aligned} \sum_{0}^{\infty} \binom{m}{n} z^{n} & = \exp\{\dfrac{1}{2}m \log(1 + 2r\cos\theta + r^{2})\} \operatorname{Cis} \left\{m\arctan\left(\frac{r\sin\theta}{1 + r\cos\theta}\right)\right\} \\ & = (1 + 2r\cos\theta + r^{2})^{\frac{1}{2}m} \operatorname{Cis} \left\{m\arctan\left(\frac{r\sin\theta}{1 + r\cos\theta}\right)\right\} \end{aligned} \] を得る。タンジェントの逆関数は \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) の値を取る。特に \(\theta = \frac{1}{2}\pi,\ z = ir\) として実部と虚部をそれぞれ比較すると \[ \begin{aligned} 1 - \binom{m}{2} r^{2} + \binom{m}{4} r^{4} - \cdots & = (1 + r^{2})^{\frac{1}{2}m} \cos(m\arctan r), \\ \binom{m}{1} r - \binom{m}{3} r^{3} + \binom{m}{5} r^{5} - \cdots & = (1 + r^{2})^{\frac{1}{2}m} \sin(m\arctan r) \end{aligned} \] を得る。
-
問題 1 の公式を \(m = 1,\ 2,\ 3\) について確認せよ。 [もちろん \(m\) が正の整数なら級数は有限となる]
-
次の等式を \(0 \leq r \lt 1\) に対して示せ: \[ \begin{aligned} 1 - \frac{1·3}{2·4} r^{2} + \frac{1·3·5·7}{2·4·6·8} r^{4} - \cdots & = \sqrt{\frac{\sqrt{1 + r^{2}} + 1}{2(1 + r^{2})}}, \\ \frac{1}{2} r - \frac{1·3·5}{2·4·6} r^{3} + \frac{1·3·5·7·9}{2·4·6·8·10} r^{5} - \cdots & = \sqrt{\frac{\sqrt{1 + r^{2}} - 1}{2(1 + r^{2})}} \end{aligned} \] [問題 1 の最後の二つの公式で \(m = -\dfrac{1}{2}\) とする]
-
次の等式を \(-\dfrac{1}{4}\pi \lt \theta \lt \dfrac{1}{4}\pi\) に対して示せ: \[ \begin{aligned} \cos m\theta & = \cos^{m} \theta \left\{1 - \binom{m}{2} \tan^{2} \theta + \binom{m}{4} \tan^{4} \theta - \cdots\right\}, \\ \sin m\theta & = \cos^{m} \theta \left\{\binom{m}{1} \tan\theta - \binom{m}{3} \tan^{3} \theta + \cdots\right\} \end{aligned} \] \(m\) は任意の実数とする。 [等式 \[ \cos m\theta + i\sin m\theta = (\cos\theta + i\sin\theta )^{m} = \cos^{m} \theta(1 + i\tan\theta)^{m} \] から直ちに従う]
-
例 81.6 では級数の積を直接計算することで、\(|z| \lt 1\) なら関数 \(f(m, z) = \sum\dbinom{m}{n} z^{n}\) が関数方程式 \[ f(m, z) f(m', z) = f(m + m', z) \] を満たすと示した。ここから §216 と同様の議論で実数の有理数 \(m\) に対する等式 \[ f(m, z) = \exp\{m\log(1 + z)\} \] を §237 の結果を使わずに導け。
-
\(z\) と \(\mu\) が実数で \(-1 \lt z \lt 1\) なら \[ \sum \binom{i\mu}{n} z^{n} = \cos\{\mu\log(1 + z)\} + i\sin\{\mu\log(1 + z)\} \] が成り立つ。
第十章に関するその他の例
-
\(i^{\log(1+i)}\) の実部が \[ e^{(4k+1)\pi^{2}/8 } \cos \{\dfrac{1}{4}(4k + 1)\pi\log 2\} \] だと示せ。\(k\) は任意の整数を表す。
-
\(c^{2} \gt a^{2} + b^{2}\) を満たす実数 \(a,\ b,\ c\) で \(a\cos\theta + b\sin\theta + c = 0\) が成り立つなら \[ \theta = m\pi + \alpha ± i\log \frac{|c| + \sqrt{c^{2} - a^{2} - b^{2}}}{\sqrt{a^{2} + b^{2}}} \] となる。\(m\) は \(c\) が正なら任意の奇数であり、\(c\) が負なら任意の偶数となる。\(\alpha\) はコサインが \(a/\sqrt{a^{2} + b^{2}}\) でサインが \(b/\sqrt{a^{2} + b^{2}}\) である角度を表す。
-
\(\theta\) が実数で \(\sin\theta \sin\phi = 1\) なら \[ \phi = (k + \dfrac{1}{2})\pi ± i\log \cot \dfrac{1}{2}(k\pi + \theta) \] だと示せ。\(k\) は \(\sin\theta\) が正なら任意の偶数を表し、\(\sin\theta\) が負なら任意の奇数を表す。
-
\(x\) が実数なら \[ \begin{gathered} \frac{d}{dx} \exp\{(a + ib)x\} = (a + ib) \exp\{(a + ib) x\}, \\ \int \exp \{(a + ib)x\}\, dx = \frac{\exp{(a + ib)x}}{a + ib} \end{gathered} \] だと示せ。ここから 例 87.3 の結果を導け。
-
\(a \gt 0\) なら \(\displaystyle\int_{0}^{\infty} \exp\{-(a + ib)x\}\, dx = \frac{1}{a + ib}\) だと示し、例 87.5 の結果を導け。
-
\((x/a)^{2} + (y/b)^{2} = 1\) が楕円の方程式で、\(f(x, y)\) が他の代数曲線の方程式の最高次の項とする。楕円と曲線の交点における離心角 (eccentric angle) の和が \[ -i\{\log f(a, ib) - \log f(a, -ib)\} \] から \(2\pi\) の倍数だけ離れることを示せ。 [離心角を \(\alpha\) とすれば \(f(a\cos\alpha, b\sin\alpha) + \cdots = 0\) だから、\(u = \exp i\alpha\) とすれば \[ f\left\{\dfrac{1}{2} a \left(u + \frac{1}{u}\right),\ -\dfrac{1}{2} ib \left(u - \frac{1}{u}\right) \right\} + \cdots = 0 \] が成り立つ。この方程式の根の積を \(P\) とすると \(\sum\alpha\) は \(-i \operatorname{Log} P\) の一つとなる]
-
方程式 \(\tan z = az\) の根の個数を求め、値を近似的に求めよ。\(a\) は実数とする。
[例 17.4 ではこの方程式に実数の根が無限にあることを示した。\(z = x + iy\) として実部と虚部をそれぞれ比較すると \[ \frac{\sin 2x}{\cos 2x + \cosh 2y} = ax,\quad \frac{\sinh 2y}{\cos 2x + \cosh 2y} = ay \] を得る。よって \(x\) と \(y\) がどちらも \(0\) でないなら \[ \frac{\sin 2x}{2x} = \frac{\sinh 2y}{2y} \] となるが、左辺は \(1\) より小さく右辺は \(1\) より大きいのでこれはあり得ない。よって \(x = 0\) または \(y = 0\) であり、もし \(y = 0\) なら最初に考えた実数解が得られる。\(x = 0\) なら方程式は \(\tanh y = ay\) となり、この方程式は \(a \leq 0\) または \(a \geq 1\) なら一つの根 \(0\) を持ち、\(0 \lt a \lt 1\) なら \(0\) 以外に二つの根を持つ。以上より \(0 \lt a \lt 1\) なら二つの純虚根を持ち、それ以外の場合は全ての根が実数となる]
-
\(a\) と \(b\) が実数で \(b\) は \(0\) でないとする。このとき \(a \leq 0\) なら方程式 \(\tan z = az + b\) は複素根を持たない。\(a \gt 0\) なら全ての複素根の実部は \(|b/2a|\) より大きくなる。
-
\(a\) を実数とする。方程式 \(\tan z = a/z\) は複素根を持たないが、\(a \lt 0\) なら二つの純虚根を持つ。
-
\(a\) と \(c\) を実数とする。方程式 \(\tan z = a\tanh cz\) は実根と純虚根を無限に持つが、複素根は持たない。
-
\(x\) が実数なら \[ e^{ax} \cos bx = \sum_{0}^{\infty} \frac{x^{n}}{n!} \left\{ a^{n} - \binom{n}{2} a^{n-2} b^{2} + \binom{n}{4} a^{n-4} b^{4} - \cdots \right\} \] だと示せ。中括弧の中には \(\frac{1}{2}(n + 1)\) 個または \(\frac{1}{2}(n + 2)\) 個の項がある。\(e^{ax} \sin bx\) に対する同様の級数を示せ。
-
\(n \to \infty\) で \(n\phi(z, n) \to z\) なら \(\{1 + \phi(z, n)\}^{n} \to \exp z\) が成り立つ。
-
\(\phi(t)\) を実数変数 \(t\) の複素関数とする。このとき \[ \frac{d}{dt} \log \phi(t) = \frac{\phi'(t)}{\phi(t)} \] が成り立つ。 [等式 \[ \phi = \psi + i\chi,\quad \log \phi = \dfrac{1}{2}\log(\psi^{2} + \chi^{2}) + i\arctan(\chi/\psi) \] を使う]
-
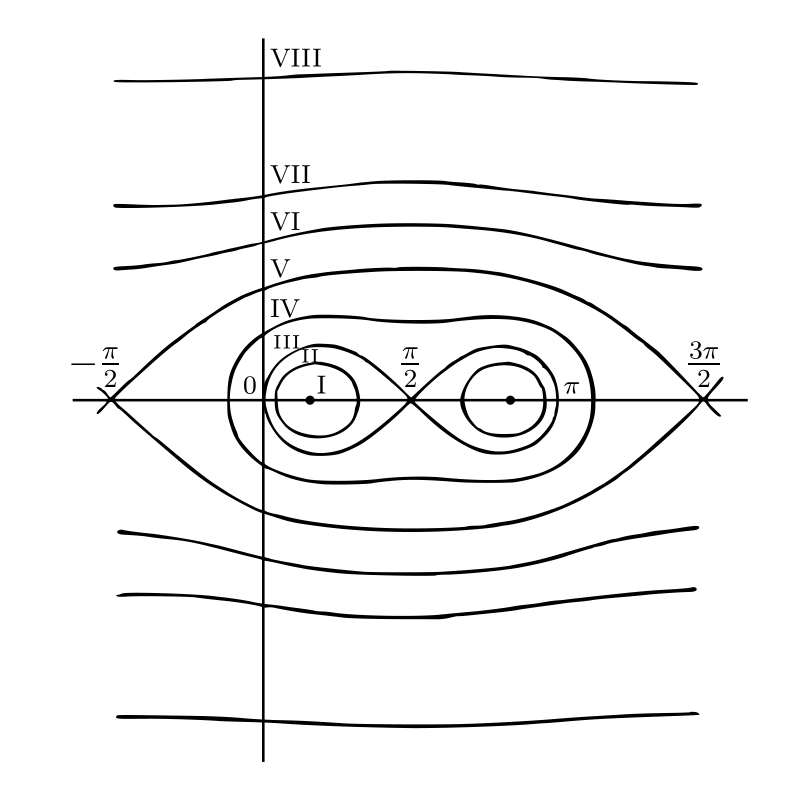
変形: 第三章の 例 21.21 や その他の例 22 では、関係 \(z = F(Z)\) で結び付いた二つの変数 \(z\) と \(Z\) に対して、それぞれの平面上にある図形の幾何学的な対応関係を考えた。ここでは関係が対数関数・指数関数・三角関数を含む場合を考える。
最初に正の \(a\) に対する \[ z = \exp(\pi Z/a),\quad Z = (a/\pi) \operatorname{Log} z \] を考える。一つの \(Z\) には一つの \(z\) が対応するが、一つの \(z\) には無限に多くの \(Z\) が対応する。\(z\) の座標を \(x,\ y,\ r,\ \theta\) として \(Z\) の座標を \(X,\ Y,\ R,\ \Theta\) とすると、\(k\) を任意の整数として \[ \begin{alignedat}{2} x & = e^{\pi X/a} \cos(\pi Y/a),\qquad & y & = e^{\pi X/a} \sin(\pi Y/a),\\ X & = (a/\pi) \log r, & Y & = (a\theta/\pi) + 2ka \end{alignedat} \] が成り立つ。\(-\pi \lt \theta \leq \pi\) で \(\operatorname{Log} z\) が主値 \(\log z\) を取るとする。このとき \(k = 0\) であり、\(Z\) は原点から両方向に \(a\) の幅を持つ \(x\) 軸と平行な領域に収まる。この領域に対応する点 \(z\) を集めると \(z\) 平面全体となり、その逆も成り立つ。\(\operatorname{Log} z\) を主値でない値とすると、\(z\) 平面全体と \(Z\) 平面内の幅 \(2a\) の領域の間の同じような対応関係が得られる。
-
前問の変形において \(Z\) 平面内の直線が \(z\) 平面上の対数螺旋に対応すると示せ。
-
同様に変形 \(z = c\cosh(\pi Z/a)\) を議論せよ。具体的には \(z\) 平面全体が \(Z\) 平面内の無限個の領域に対応し、その領域のそれぞれが \(x\) 軸に平行で幅が \(2a\) だと示せ。さらに直線 \(X = X_{0}\) が楕円 \[ \left\{\frac{x}{c\cosh(\pi X_{0}/a)}\right\}^{2} + \left\{\frac{y}{c\sinh(\pi X_{0}/a)}\right\}^{2} = 1 \] に対応すること、異なる \(X_{0}\) の値に対応する楕円が共通の焦点を持つこと、直線 \(Y = Y_{0}\) が同じ焦点の双曲線に対応することを示せ。二つの焦点を結ぶ線分および \(x\) 軸のそれ以外の部分に対応する退化した楕円および双曲線を \(z\) が移動するとき、\(Z\) はどのように変化するか?
-
問題 16 の結果が問題 14 および第三章のその他の例 25 と合致することを示せ。 [変形 \(z = c\cosh(\pi Z/a)\) は \[ z = cz_{1},\quad z_{1} = \dfrac{1}{2}\{z_{2} + (1/z_{2})\},\quad z_{2} = \exp(\pi Z/a) \] という変形の合成だとみなせる]
-
変形 \(z = c\tanh(\pi Z/a)\) について同様に議論せよ。直線 \(X = X_{0}\) には共通の軸を持つ円 \[ \{x - c\coth(2\pi X_{0}/a)\}^{2} + y^{2} = c^{2} \operatorname{cosech}^{2}(2\pi X_{0}/a) \] が対応することを示せ。さらに直線 \(Y = Y_{0}\) には共通の軸を持つ円が対応し、その軸が \(X = X_{0}\) に対応する円の軸と直行することを示せ。
-
ステレオ投影とメルカトル投影: 原点中心の半径 \(1\) の球の各点が、南極 (座標が \((0,\ 0,\ 1)\) の点) から北極の接平面に向かって射影されている。球上の点の座標は \((\xi,\ \eta,\ \zeta)\) であり、北極の接平面に直交軸 \(OX,\ OY\) が \(\xi\) と \(\eta\) の軸に平行に取られている。射影された点の座標が \[ x = \frac{2\xi}{1 + \zeta},\quad y = \frac{2\eta}{1 + \zeta} \] であることを示せ。さらに考えている球上の点の平面 \(\eta = 0\) から測った経度を \(\phi\)、北極距離 (north polar distance) を \(\theta\) とすれば \(x + iy = 2\tan \frac{1}{2}\theta \operatorname{Cis}\phi\) が成り立つと示せ。
この射影は接平面に球の地図を与える。この地図をステレオ投影 (Stereographic Projection) と呼ぶ。さらに新しい複素変数 \[ Z = X + iY = -i\log \dfrac{1}{2}z = -i\log \dfrac{1}{2}(x + iy) \] を導入すれば \(X = \phi,\ Y = \log \cot \frac{1}{2}\theta\) であり、\(Z\) 平面上にはメルカトル投影 (Mercator's Projection) と呼ばれる異なる地図が得られる。この地図では緯度と経度に平行な直線がそれぞれ \(X\) と \(Y\) に平行な直線となる。
-
次の等式で与えられる変形を議論せよ: \[ z = \operatorname{Log} \left(\frac{Z - a}{Z - b}\right) \] \(x\) と \(y\) が定数になる直線に対応するのが \(Z\) 平面における軸が共通な直行する円の系だと示せ。
-
変形 \[ z = \operatorname{Log} \left\{\frac{\sqrt{Z - a} + \sqrt{Z - b}}{\sqrt{b - a}}\right\} \] を議論せよ。\(x\) と \(y\) が定数になる直線に対応するのが \(Z = a\) と \(Z = b\) を共通の焦点に持つ楕円または双曲線の集合だと示せ。
[仮定から \[ \begin{alignedat}{2} \sqrt{Z - a} + \sqrt{Z - b} & = \sqrt{b - a}\, \exp(& & x + iy), \\ \sqrt{Z - a} - \sqrt{Z - b} & = \sqrt{b - a}\, \exp(& - & x - iy) \end{alignedat} \] であり、ここから \[ \begin{aligned} |Z - a| + |Z - b| & = |b - a|\cosh 2x,\\ |Z - a| - |Z - b| & = |b - a|\cos 2y \end{aligned} \] が得られる]
-
変形 \(\bm{z = Z^{i}}\): \(z = Z^{i}\) で虚部が主値を取るとすれば \[ \exp(\log r + i\theta) = z = \exp(i\log Z) = \exp(i\log R - \Theta) \] より整数 \(k\) に対して \(\log r = -\Theta,\ \theta = \log R + 2k\pi\) を得る。\(k\) をどんな値としても点 \(z\) は変わらないから、\(k = 0\) と定める。すると \[ \log r = -\Theta,\quad \theta = \log R \qquad \text{(1)} \] である。
\(Z\) が \(Z\) 平面全体を覆うには、\(R\) が正の実数全体を動き、\(\Theta\) が \(-\pi\) から \(\pi\) の間を動けばよい。このとき \(r\) は \(\exp(-\pi)\) から \(\exp\pi\) を動き、\(\theta\) は実数全体を動く。そのため \(Z\) 平面全体は \(r = \exp(-\pi)\) と \(r = \exp\pi\) という二つの円の間の環に対応する。この環は無限回覆われるが、もし \(\theta\) が \(-\pi\) と \(\pi\) の間だけを動くとすれば一度だけ覆われる。このとき \(R\) は \(\exp(-\pi)\) から \(\exp \pi\) に動くから、\(Z\) の変動は \(z\) の変動と相似な環に制限される。さらに二つの環のそれぞれは負の \(z\) (および \(Z\)) 軸上に除外される点を持つ。偏角が \(-\pi\) と \(\pi\) を越えられないためである。
よって二つの環の間の対応関係は次の等式で与えられる: \[ z = Z^{i},\quad Z = z^{-i} \] どちらの指数も主値を考える。いずれかの平面における原点を中心とする円はもう一つの平面における原点を通る直線に対応する。
-
前問の変形を考える。\(Z\) が点 \(\exp \pi\) から始まって点 \(-\exp \pi\) まで大円上を移動し、負軸上を移動し、小円上を一周し、負軸上を戻り、大円上のまだ通っていない部分通って \(\exp \pi\) 戻るとき、\(z\) がどう動くか調べよ。
-
半径が次の値の円で \(z\) 平面と \(Z\) 平面を無限個の環に分割する: \[ \ldots, \quad e^{-(2n+1)\pi},\quad\ldots,\quad e^{-\pi},\quad e^{\pi},\quad e^{3\pi},\quad\ldots,\quad e^{(2n+1)\pi},\quad\ldots \] 等式 \(z = Z^{i},\ Z = z^{-i}\) において適切な指数の値を考えることで、いずれかの平面における環をもう一方の平面における任意の環に対応させる方法を示せ。
-
\(z = Z^{i}\) で任意の指数を考えるなら、\(Z\) 平面上の原点が極の対数螺旋上を \(Z\) が動くとき、\(z\) も \(z\) 平面上の原点が極の対数螺旋上を動くことを示せ。
-
\(a\) を実数とする。\(z\) が実軸を通って原点に近づくとき、\(Z = z^{ai}\) はどのように振る舞うか? [\(Z\) は原点中心の円上を動く (\(z^{ai}\) が主値を取るなら単位円となる)。\(Z\) の実部と虚部はどちらも有限に振動する]
-
\(Z = z^{a + bi}\) に対する同じ問題を考えよ。\(a\) と \(b\) は任意の実数とする。
-
\(a\) を実数とする。\(\sum\limits_{-\infty}^{\infty} a_{n}z^{nai}\) という形をした級数が収束する領域が角度で表せる、つまり \(\theta_{0} \lt \arg z \lt \theta_{1}\) という形の不等式で囲まれる領域だと示せ。 [この角度が直線あるいは平面全体になることもある]
-
等位線: 複素変数 \(z\) の関数 \(f(z)\) について、\(|f(z)|\) が定数になる曲線を \(f(z)\) の等位線 (level curve) と呼ぶ。次の関数の等位線を描け: \[ \begin{alignedat}{2} z - a \quad & (\text{同心円}), \qquad& (z - a)(z - b) \quad & (\text{デカルトの卵形線}), \\ (z - a)/(z - b) \quad & (\text{同軸楕円}), \qquad& \exp z \quad & (\text{直線}) \end{alignedat} \]
-
\((z - a)(z - b)(z - c)\) と \((1 + z\sqrt{3} + z^{2})/z\) の等位線を描け。 [後者の等位線を 図 59 に示す。\(\text{(i)}\)–\(\text{(vii)}\) はそれぞれ \(|f(z)|\) が \[ .10,\quad 2 - \sqrt{3} = .27,\quad .40,\quad 1.00,\quad 2.00,\quad 2 + \sqrt{3} = 3.73,\quad 4.53 \] の等位線である。読者はおそらく任意の有理関数の等位線の形を一般的に容易に想像できると思うが、詳細に立ち入るには複素変数の関数の一般理論が必要になる]
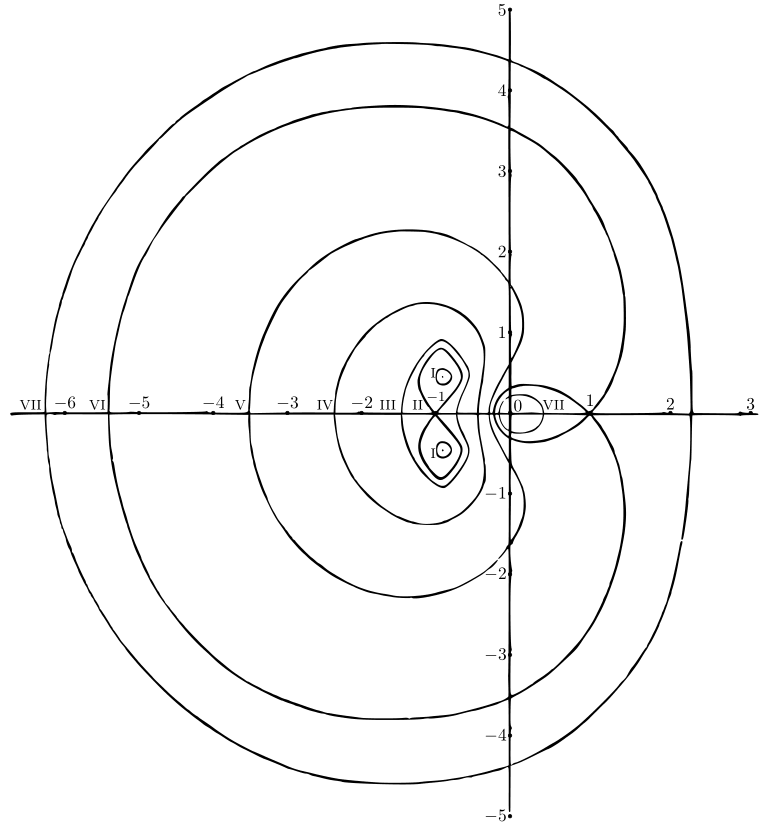 図 59
図 59 -
(i) \(z\exp z\) と (ii) \(\sin z\) の等位線を描け。 [\(\sin z\) の等位線を 図 60 に示す。\(\text{(i)}\)–\(\text{(viii)}\) は \(k = .35,\ .50,\ .71,\ 1.00,\ 1.41,\ 2.00,\ 2.83,\ 4.00\) に対応する等位線である]
-
\(\exp z = c\) の等位線を描け。\(c\) は実数とする。 [\(\exp z - 1\) の等位線を 図 61 に示す。\(\text{(i)}\)–\(\text{(vii)}\) はそれぞれ \(\log k = -1.00,\ -.20,\ -.05,\ 0.00,\ .05,\ .20,\ 1.00\) となる \(k\) に対応する]
-
正の定数 \(c\) に対する \(\sin z - c\) の等位線は 図 62 と 図 63 のようになる。 [この等位線の概形は \(c \lt 1\) か \(c \gt 1\) かによって変わる。図 62 では \(c = .5\) であり、\(\text{(i)}\)–\(\text{(viii)}\) は \(k = .29,\ .37,\ .50,\ .87,\ 1.50,\ 2.60,\ 4.50,\ 7.79\) に対応する。図 63 では \(c = 2\) であり、\(\text{(i)}\)–\(\text{(vii)}\) は \(k = .58,\ 1.00,\ 1.73,\ 3.00,\ 5.20,\ 9.00,\ 15.59\) に対応する。\(c = 1\) の場合の等位線は 図 60 の縮尺と原点を変えたものになる]
-
\(0 \lt \theta \lt \pi\) なら \[ \begin{alignedat}{3} \cos\theta & + \dfrac{1}{3} \cos 3\theta & & + \dfrac{1}{5} \cos 5\theta & & + \cdots = \dfrac{1}{4} \log \cot^{2}\dfrac{1}{2}\theta,\\ \sin\theta & + \dfrac{1}{3} \sin 3\theta & & + \dfrac{1}{5} \sin 5\theta & & + \cdots = \dfrac{1}{4}\pi \end{alignedat} \] だと示し、級数が収束する他の全ての \(\theta\) に対する級数の和を求めよ。 [\(z = \cos\theta + i\sin\theta\) に対する等式 \[ z + \dfrac{1}{3}z^{3} + \dfrac{1}{5}z^{5} + \cdots = \dfrac{1}{2} \log \left(\frac{1 + z}{1 - z}\right) \] を使う。\(\theta\) が \(\pi\) 増加すると、二つの級数の和はそれぞれ符号が逆転する。ここから一つ目の等式は \(\pi\) の倍数の \(\theta\) 以外で成り立ち (\(\pi\) の倍数なら級数は発散する)、二つ目の級数の和は \(2k\pi \lt \theta \lt (2k + 1)\pi\) なら \(\frac{1}{4}\pi\) で \((2k + 1)\pi \lt \theta \lt (2k + 2)\pi\) なら \(-\frac{1}{4}\pi\) だと分かる (\(\theta\) が \(\pi\) の倍数なら和は \(0\) になる)]
-
\(0 \lt \theta \lt \frac{1}{2}\pi\) なら \[ \begin{alignedat}{3} \cos\theta & - \dfrac{1}{3} \cos 3\theta & & + \dfrac{1}{5} \cos 5\theta & & - \cdots = \dfrac{1}{4}\pi,\\ \sin\theta & - \dfrac{1}{3} \sin 3\theta & & + \dfrac{1}{5} \sin 5\theta & & - \cdots = \dfrac{1}{4} \log (\sec\theta + \tan\theta)^{2} \end{alignedat} \] だと示し、級数が収束する他の全ての \(\theta\) に対する和を求めよ。
-
次を示せ: \[ \cos\theta \cos\alpha + \dfrac{1}{2} \cos 2\theta \cos 2\alpha + \dfrac{1}{3} \cos 3\theta \cos 3\alpha + \cdots = -\dfrac{1}{4} \log \{4(\cos\theta - \cos\alpha)^{2}\} \] \(\theta - \alpha\) と \(\theta + \alpha\) はどちらも \(2\pi\) の倍数でないとする。
-
\(a\) と \(b\) がどちらも実数でないとする。このとき \[ \int_{0}^{\infty} \frac{dx}{(x - a)(x - b)} = -\frac{\log(-a) - \log(-b)}{a - b} \] を示せ。二つの対数は主値を取る。正の実数 \(c\) に対する \(a = ci\) および \(b = -ci\) でこの結果を確認せよ。\(a\) と \(b\) が負の実数の場合を同様に議論せよ。
-
\(\alpha\) と \(\beta\) が実数で \(\beta \gt 0\) とする。このとき \[ \int_{0}^{\infty} \frac{d}{x^{2} - (\alpha + i\beta)^{2}} = \frac{\pi i}{2(\alpha + i\beta)} \] を示せ。\(\beta \lt 0\) なら積分の値はどうなるか?
-
\(Ax^{2} + 2Bx + C = 0\) の二つの根が符号が逆の虚部を持つとする。このとき \[ \int_{-\infty}^{\infty} \frac{dx}{Ax^{2} + 2Bx + C} = \frac{\pi i}{\sqrt{B^{2} - AC}} \] だと示せ。ここで \(\sqrt{B^{2} - AC}\) の符号は \(\{\sqrt{B^{2} - AC}\}/Ai\) の実部が正になるように選ぶ。