第十章に関するその他の例
-
\(i^{\log(1+i)}\) の実部が \[ e^{(4k+1)\pi^{2}/8 } \cos \{\dfrac{1}{4}(4k + 1)\pi\log 2\} \] だと示せ。\(k\) は任意の整数を表す。
-
\(c^{2} \gt a^{2} + b^{2}\) を満たす実数 \(a,\ b,\ c\) で \(a\cos\theta + b\sin\theta + c = 0\) が成り立つなら \[ \theta = m\pi + \alpha ± i\log \frac{|c| + \sqrt{c^{2} - a^{2} - b^{2}}}{\sqrt{a^{2} + b^{2}}} \] となる。\(m\) は \(c\) が正なら任意の奇数であり、\(c\) が負なら任意の偶数となる。\(\alpha\) はコサインが \(a/\sqrt{a^{2} + b^{2}}\) でサインが \(b/\sqrt{a^{2} + b^{2}}\) である角度を表す。
-
\(\theta\) が実数で \(\sin\theta \sin\phi = 1\) なら \[ \phi = (k + \dfrac{1}{2})\pi ± i\log \cot \dfrac{1}{2}(k\pi + \theta) \] だと示せ。\(k\) は \(\sin\theta\) が正なら任意の偶数を表し、\(\sin\theta\) が負なら任意の奇数を表す。
-
\(x\) が実数なら \[ \begin{gathered} \frac{d}{dx} \exp\{(a + ib)x\} = (a + ib) \exp\{(a + ib) x\}, \\ \int \exp \{(a + ib)x\}\, dx = \frac{\exp{(a + ib)x}}{a + ib} \end{gathered} \] だと示せ。ここから 例 87.3 の結果を導け。
-
\(a \gt 0\) なら \(\displaystyle\int_{0}^{\infty} \exp\{-(a + ib)x\}\, dx = \frac{1}{a + ib}\) だと示し、例 87.5 の結果を導け。
-
\((x/a)^{2} + (y/b)^{2} = 1\) が楕円の方程式で、\(f(x, y)\) が他の代数曲線の方程式の最高次の項とする。楕円と曲線の交点における離心角 (eccentric angle) の和が \[ -i\{\log f(a, ib) - \log f(a, -ib)\} \] から \(2\pi\) の倍数だけ離れることを示せ。 [離心角を \(\alpha\) とすれば \(f(a\cos\alpha, b\sin\alpha) + \cdots = 0\) だから、\(u = \exp i\alpha\) とすれば \[ f\left\{\dfrac{1}{2} a \left(u + \frac{1}{u}\right),\ -\dfrac{1}{2} ib \left(u - \frac{1}{u}\right) \right\} + \cdots = 0 \] が成り立つ。この方程式の根の積を \(P\) とすると \(\sum\alpha\) は \(-i \operatorname{Log} P\) の一つとなる]
-
方程式 \(\tan z = az\) の根の個数を求め、値を近似的に求めよ。\(a\) は実数とする。
[例 17.4 ではこの方程式に実数の根が無限にあることを示した。\(z = x + iy\) として実部と虚部をそれぞれ比較すると \[ \frac{\sin 2x}{\cos 2x + \cosh 2y} = ax,\quad \frac{\sinh 2y}{\cos 2x + \cosh 2y} = ay \] を得る。よって \(x\) と \(y\) がどちらも \(0\) でないなら \[ \frac{\sin 2x}{2x} = \frac{\sinh 2y}{2y} \] となるが、左辺は \(1\) より小さく右辺は \(1\) より大きいのでこれはあり得ない。よって \(x = 0\) または \(y = 0\) であり、もし \(y = 0\) なら最初に考えた実数解が得られる。\(x = 0\) なら方程式は \(\tanh y = ay\) となり、この方程式は \(a \leq 0\) または \(a \geq 1\) なら一つの根 \(0\) を持ち、\(0 \lt a \lt 1\) なら \(0\) 以外に二つの根を持つ。以上より \(0 \lt a \lt 1\) なら二つの純虚根を持ち、それ以外の場合は全ての根が実数となる]
-
\(a\) と \(b\) が実数で \(b\) は \(0\) でないとする。このとき \(a \leq 0\) なら方程式 \(\tan z = az + b\) は複素根を持たない。\(a \gt 0\) なら全ての複素根の実部は \(|b/2a|\) より大きくなる。
-
\(a\) を実数とする。方程式 \(\tan z = a/z\) は複素根を持たないが、\(a \lt 0\) なら二つの純虚根を持つ。
-
\(a\) と \(c\) を実数とする。方程式 \(\tan z = a\tanh cz\) は実根と純虚根を無限に持つが、複素根は持たない。
-
\(x\) が実数なら \[ e^{ax} \cos bx = \sum_{0}^{\infty} \frac{x^{n}}{n!} \left\{ a^{n} - \binom{n}{2} a^{n-2} b^{2} + \binom{n}{4} a^{n-4} b^{4} - \cdots \right\} \] だと示せ。中括弧の中には \(\frac{1}{2}(n + 1)\) 個または \(\frac{1}{2}(n + 2)\) 個の項がある。\(e^{ax} \sin bx\) に対する同様の級数を示せ。
-
\(n \to \infty\) で \(n\phi(z, n) \to z\) なら \(\{1 + \phi(z, n)\}^{n} \to \exp z\) が成り立つ。
-
\(\phi(t)\) を実数変数 \(t\) の複素関数とする。このとき \[ \frac{d}{dt} \log \phi(t) = \frac{\phi'(t)}{\phi(t)} \] が成り立つ。 [等式 \[ \phi = \psi + i\chi,\quad \log \phi = \dfrac{1}{2}\log(\psi^{2} + \chi^{2}) + i\arctan(\chi/\psi) \] を使う]
-
変形: 第三章の 例 21.21 や その他の例 22 では、関係 \(z = F(Z)\) で結び付いた二つの変数 \(z\) と \(Z\) に対して、それぞれの平面上にある図形の幾何学的な対応関係を考えた。ここでは関係が対数関数・指数関数・三角関数を含む場合を考える。
最初に正の \(a\) に対する \[ z = \exp(\pi Z/a),\quad Z = (a/\pi) \operatorname{Log} z \] を考える。一つの \(Z\) には一つの \(z\) が対応するが、一つの \(z\) には無限に多くの \(Z\) が対応する。\(z\) の座標を \(x,\ y,\ r,\ \theta\) として \(Z\) の座標を \(X,\ Y,\ R,\ \Theta\) とすると、\(k\) を任意の整数として \[ \begin{alignedat}{2} x & = e^{\pi X/a} \cos(\pi Y/a),\qquad & y & = e^{\pi X/a} \sin(\pi Y/a),\\ X & = (a/\pi) \log r, & Y & = (a\theta/\pi) + 2ka \end{alignedat} \] が成り立つ。\(-\pi \lt \theta \leq \pi\) で \(\operatorname{Log} z\) が主値 \(\log z\) を取るとする。このとき \(k = 0\) であり、\(Z\) は原点から両方向に \(a\) の幅を持つ \(x\) 軸と平行な領域に収まる。この領域に対応する点 \(z\) を集めると \(z\) 平面全体となり、その逆も成り立つ。\(\operatorname{Log} z\) を主値でない値とすると、\(z\) 平面全体と \(Z\) 平面内の幅 \(2a\) の領域の間の同じような対応関係が得られる。
-
前問の変形において \(Z\) 平面内の直線が \(z\) 平面上の対数螺旋に対応すると示せ。
-
同様に変形 \(z = c\cosh(\pi Z/a)\) を議論せよ。具体的には \(z\) 平面全体が \(Z\) 平面内の無限個の領域に対応し、その領域のそれぞれが \(x\) 軸に平行で幅が \(2a\) だと示せ。さらに直線 \(X = X_{0}\) が楕円 \[ \left\{\frac{x}{c\cosh(\pi X_{0}/a)}\right\}^{2} + \left\{\frac{y}{c\sinh(\pi X_{0}/a)}\right\}^{2} = 1 \] に対応すること、異なる \(X_{0}\) の値に対応する楕円が共通の焦点を持つこと、直線 \(Y = Y_{0}\) が同じ焦点の双曲線に対応することを示せ。二つの焦点を結ぶ線分および \(x\) 軸のそれ以外の部分に対応する退化した楕円および双曲線を \(z\) が移動するとき、\(Z\) はどのように変化するか?
-
問題 16 の結果が問題 14 および第三章のその他の例 25 と合致することを示せ。 [変形 \(z = c\cosh(\pi Z/a)\) は \[ z = cz_{1},\quad z_{1} = \dfrac{1}{2}\{z_{2} + (1/z_{2})\},\quad z_{2} = \exp(\pi Z/a) \] という変形の合成だとみなせる]
-
変形 \(z = c\tanh(\pi Z/a)\) について同様に議論せよ。直線 \(X = X_{0}\) には共通の軸を持つ円 \[ \{x - c\coth(2\pi X_{0}/a)\}^{2} + y^{2} = c^{2} \operatorname{cosech}^{2}(2\pi X_{0}/a) \] が対応することを示せ。さらに直線 \(Y = Y_{0}\) には共通の軸を持つ円が対応し、その軸が \(X = X_{0}\) に対応する円の軸と直行することを示せ。
-
ステレオ投影とメルカトル投影: 原点中心の半径 \(1\) の球の各点が、南極 (座標が \((0,\ 0,\ 1)\) の点) から北極の接平面に向かって射影されている。球上の点の座標は \((\xi,\ \eta,\ \zeta)\) であり、北極の接平面に直交軸 \(OX,\ OY\) が \(\xi\) と \(\eta\) の軸に平行に取られている。射影された点の座標が \[ x = \frac{2\xi}{1 + \zeta},\quad y = \frac{2\eta}{1 + \zeta} \] であることを示せ。さらに考えている球上の点の平面 \(\eta = 0\) から測った経度を \(\phi\)、北極距離 (north polar distance) を \(\theta\) とすれば \(x + iy = 2\tan \frac{1}{2}\theta \operatorname{Cis}\phi\) が成り立つと示せ。
この射影は接平面に球の地図を与える。この地図をステレオ投影 (Stereographic Projection) と呼ぶ。さらに新しい複素変数 \[ Z = X + iY = -i\log \dfrac{1}{2}z = -i\log \dfrac{1}{2}(x + iy) \] を導入すれば \(X = \phi,\ Y = \log \cot \frac{1}{2}\theta\) であり、\(Z\) 平面上にはメルカトル投影 (Mercator's Projection) と呼ばれる異なる地図が得られる。この地図では緯度と経度に平行な直線がそれぞれ \(X\) と \(Y\) に平行な直線となる。
-
次の等式で与えられる変形を議論せよ: \[ z = \operatorname{Log} \left(\frac{Z - a}{Z - b}\right) \] \(x\) と \(y\) が定数になる直線に対応するのが \(Z\) 平面における軸が共通な直行する円の系だと示せ。
-
変形 \[ z = \operatorname{Log} \left\{\frac{\sqrt{Z - a} + \sqrt{Z - b}}{\sqrt{b - a}}\right\} \] を議論せよ。\(x\) と \(y\) が定数になる直線に対応するのが \(Z = a\) と \(Z = b\) を共通の焦点に持つ楕円または双曲線の集合だと示せ。
[仮定から \[ \begin{alignedat}{2} \sqrt{Z - a} + \sqrt{Z - b} & = \sqrt{b - a}\, \exp(& & x + iy), \\ \sqrt{Z - a} - \sqrt{Z - b} & = \sqrt{b - a}\, \exp(& - & x - iy) \end{alignedat} \] であり、ここから \[ \begin{aligned} |Z - a| + |Z - b| & = |b - a|\cosh 2x,\\ |Z - a| - |Z - b| & = |b - a|\cos 2y \end{aligned} \] が得られる]
-
変形 \(\bm{z = Z^{i}}\): \(z = Z^{i}\) で虚部が主値を取るとすれば \[ \exp(\log r + i\theta) = z = \exp(i\log Z) = \exp(i\log R - \Theta) \] より整数 \(k\) に対して \(\log r = -\Theta,\ \theta = \log R + 2k\pi\) を得る。\(k\) をどんな値としても点 \(z\) は変わらないから、\(k = 0\) と定める。すると \[ \log r = -\Theta,\quad \theta = \log R \qquad \text{(1)} \] である。
\(Z\) が \(Z\) 平面全体を覆うには、\(R\) が正の実数全体を動き、\(\Theta\) が \(-\pi\) から \(\pi\) の間を動けばよい。このとき \(r\) は \(\exp(-\pi)\) から \(\exp\pi\) を動き、\(\theta\) は実数全体を動く。そのため \(Z\) 平面全体は \(r = \exp(-\pi)\) と \(r = \exp\pi\) という二つの円の間の環に対応する。この環は無限回覆われるが、もし \(\theta\) が \(-\pi\) と \(\pi\) の間だけを動くとすれば一度だけ覆われる。このとき \(R\) は \(\exp(-\pi)\) から \(\exp \pi\) に動くから、\(Z\) の変動は \(z\) の変動と相似な環に制限される。さらに二つの環のそれぞれは負の \(z\) (および \(Z\)) 軸上に除外される点を持つ。偏角が \(-\pi\) と \(\pi\) を越えられないためである。
よって二つの環の間の対応関係は次の等式で与えられる: \[ z = Z^{i},\quad Z = z^{-i} \] どちらの指数も主値を考える。いずれかの平面における原点を中心とする円はもう一つの平面における原点を通る直線に対応する。
-
前問の変形を考える。\(Z\) が点 \(\exp \pi\) から始まって点 \(-\exp \pi\) まで大円上を移動し、負軸上を移動し、小円上を一周し、負軸上を戻り、大円上のまだ通っていない部分通って \(\exp \pi\) 戻るとき、\(z\) がどう動くか調べよ。
-
半径が次の値の円で \(z\) 平面と \(Z\) 平面を無限個の環に分割する: \[ \ldots, \quad e^{-(2n+1)\pi},\quad\ldots,\quad e^{-\pi},\quad e^{\pi},\quad e^{3\pi},\quad\ldots,\quad e^{(2n+1)\pi},\quad\ldots \] 等式 \(z = Z^{i},\ Z = z^{-i}\) において適切な指数の値を考えることで、いずれかの平面における環をもう一方の平面における任意の環に対応させる方法を示せ。
-
\(z = Z^{i}\) で任意の指数を考えるなら、\(Z\) 平面上の原点が極の対数螺旋上を \(Z\) が動くとき、\(z\) も \(z\) 平面上の原点が極の対数螺旋上を動くことを示せ。
-
\(a\) を実数とする。\(z\) が実軸を通って原点に近づくとき、\(Z = z^{ai}\) はどのように振る舞うか? [\(Z\) は原点中心の円上を動く (\(z^{ai}\) が主値を取るなら単位円となる)。\(Z\) の実部と虚部はどちらも有限に振動する]
-
\(Z = z^{a + bi}\) に対する同じ問題を考えよ。\(a\) と \(b\) は任意の実数とする。
-
\(a\) を実数とする。\(\sum\limits_{-\infty}^{\infty} a_{n}z^{nai}\) という形をした級数が収束する領域が角度で表せる、つまり \(\theta_{0} \lt \arg z \lt \theta_{1}\) という形の不等式で囲まれる領域だと示せ。 [この角度が直線あるいは平面全体になることもある]
-
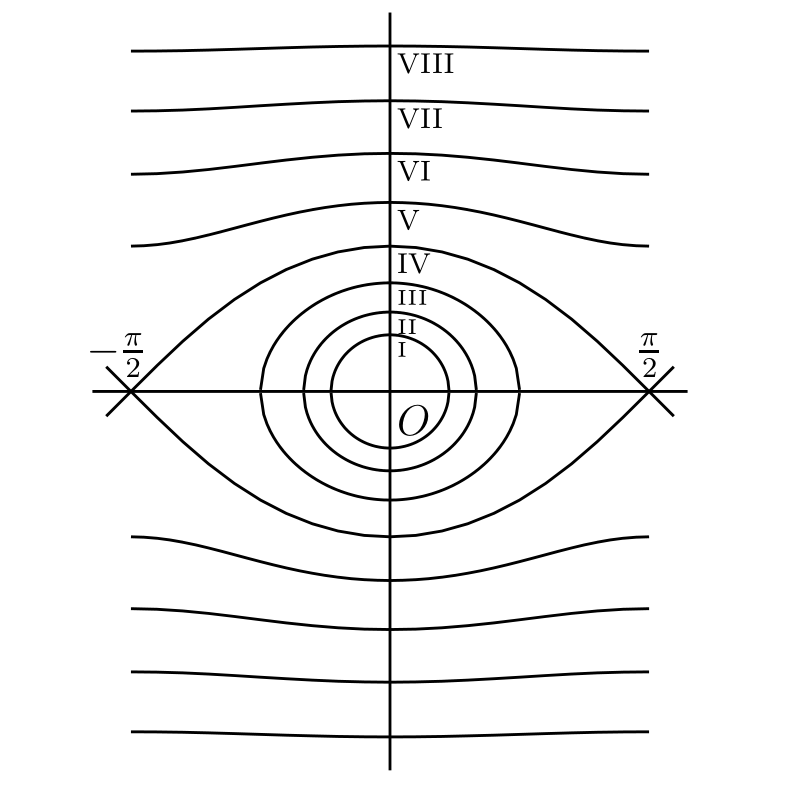
等位線: 複素変数 \(z\) の関数 \(f(z)\) について、\(|f(z)|\) が定数になる曲線を \(f(z)\) の等位線 (level curve) と呼ぶ。次の関数の等位線を描け: \[ \begin{alignedat}{2} z - a \quad & (\text{同心円}), \qquad& (z - a)(z - b) \quad & (\text{デカルトの卵形線}), \\ (z - a)/(z - b) \quad & (\text{同軸楕円}), \qquad& \exp z \quad & (\text{直線}) \end{alignedat} \]
-
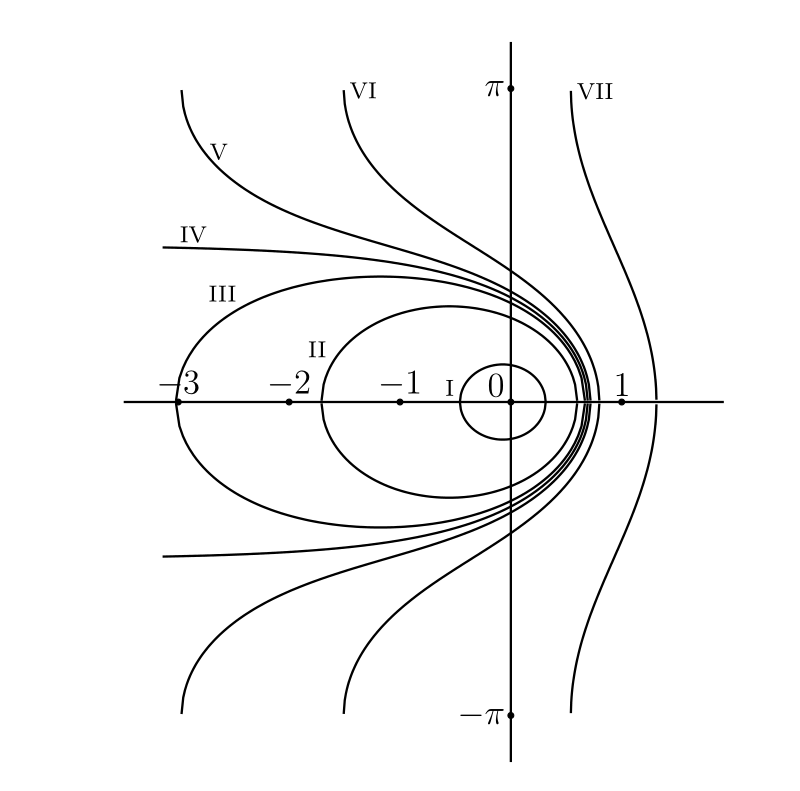
\((z - a)(z - b)(z - c)\) と \((1 + z\sqrt{3} + z^{2})/z\) の等位線を描け。 [後者の等位線を 図 59 に示す。\(\text{(i)}\)–\(\text{(vii)}\) はそれぞれ \(|f(z)|\) が \[ .10,\quad 2 - \sqrt{3} = .27,\quad .40,\quad 1.00,\quad 2.00,\quad 2 + \sqrt{3} = 3.73,\quad 4.53 \] の等位線である。読者はおそらく任意の有理関数の等位線の形を一般的に容易に想像できると思うが、詳細に立ち入るには複素変数の関数の一般理論が必要になる]
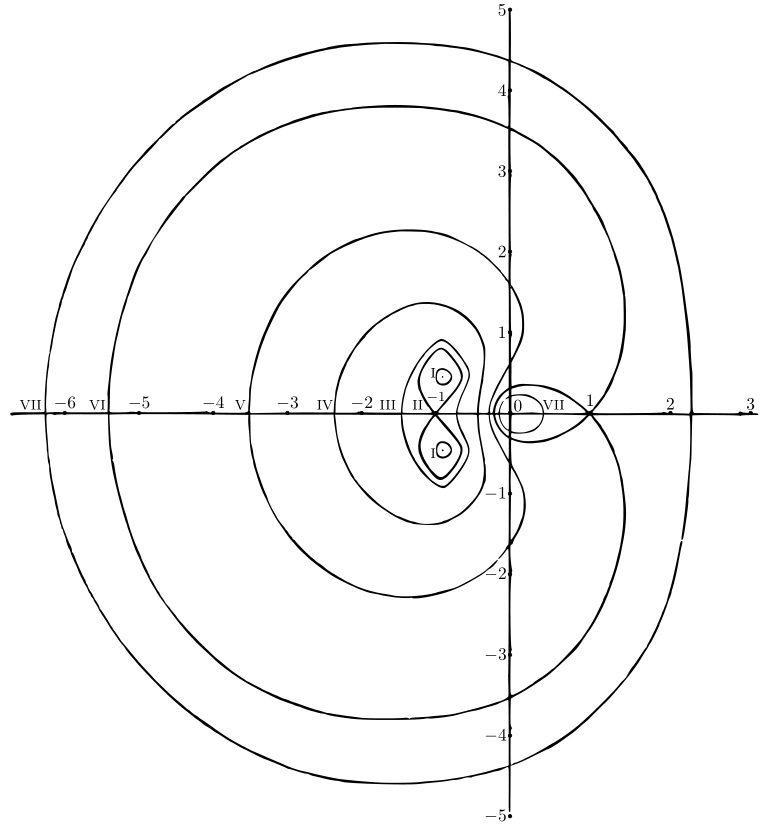 図 59
図 59 -
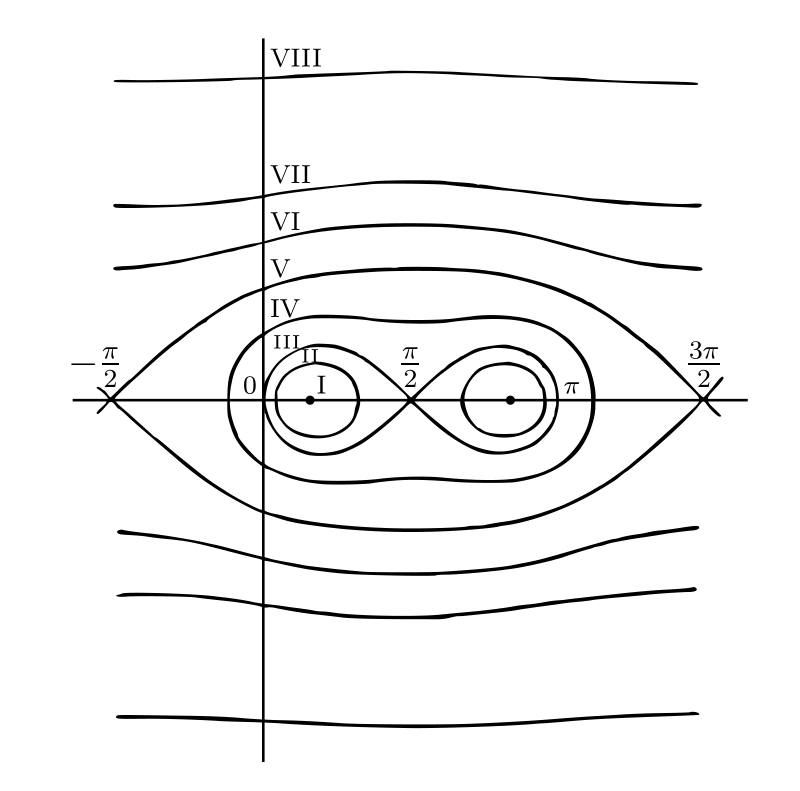
(i) \(z\exp z\) と (ii) \(\sin z\) の等位線を描け。 [\(\sin z\) の等位線を 図 60 に示す。\(\text{(i)}\)–\(\text{(viii)}\) は \(k = .35,\ .50,\ .71,\ 1.00,\ 1.41,\ 2.00,\ 2.83,\ 4.00\) に対応する等位線である]
-
\(\exp z = c\) の等位線を描け。\(c\) は実数とする。 [\(\exp z - 1\) の等位線を 図 61 に示す。\(\text{(i)}\)–\(\text{(vii)}\) はそれぞれ \(\log k = -1.00,\ -.20,\ -.05,\ 0.00,\ .05,\ .20,\ 1.00\) となる \(k\) に対応する]
-
正の定数 \(c\) に対する \(\sin z - c\) の等位線は 図 62 と 図 63 のようになる。 [この等位線の概形は \(c \lt 1\) か \(c \gt 1\) かによって変わる。図 62 では \(c = .5\) であり、\(\text{(i)}\)–\(\text{(viii)}\) は \(k = .29,\ .37,\ .50,\ .87,\ 1.50,\ 2.60,\ 4.50,\ 7.79\) に対応する。図 63 では \(c = 2\) であり、\(\text{(i)}\)–\(\text{(vii)}\) は \(k = .58,\ 1.00,\ 1.73,\ 3.00,\ 5.20,\ 9.00,\ 15.59\) に対応する。\(c = 1\) の場合の等位線は 図 60 の縮尺と原点を変えたものになる]
-
\(0 \lt \theta \lt \pi\) なら \[ \begin{alignedat}{3} \cos\theta & + \dfrac{1}{3} \cos 3\theta & & + \dfrac{1}{5} \cos 5\theta & & + \cdots = \dfrac{1}{4} \log \cot^{2}\dfrac{1}{2}\theta,\\ \sin\theta & + \dfrac{1}{3} \sin 3\theta & & + \dfrac{1}{5} \sin 5\theta & & + \cdots = \dfrac{1}{4}\pi \end{alignedat} \] だと示し、級数が収束する他の全ての \(\theta\) に対する級数の和を求めよ。 [\(z = \cos\theta + i\sin\theta\) に対する等式 \[ z + \dfrac{1}{3}z^{3} + \dfrac{1}{5}z^{5} + \cdots = \dfrac{1}{2} \log \left(\frac{1 + z}{1 - z}\right) \] を使う。\(\theta\) が \(\pi\) 増加すると、二つの級数の和はそれぞれ符号が逆転する。ここから一つ目の等式は \(\pi\) の倍数の \(\theta\) 以外で成り立ち (\(\pi\) の倍数なら級数は発散する)、二つ目の級数の和は \(2k\pi \lt \theta \lt (2k + 1)\pi\) なら \(\frac{1}{4}\pi\) で \((2k + 1)\pi \lt \theta \lt (2k + 2)\pi\) なら \(-\frac{1}{4}\pi\) だと分かる (\(\theta\) が \(\pi\) の倍数なら和は \(0\) になる)]
-
\(0 \lt \theta \lt \frac{1}{2}\pi\) なら \[ \begin{alignedat}{3} \cos\theta & - \dfrac{1}{3} \cos 3\theta & & + \dfrac{1}{5} \cos 5\theta & & - \cdots = \dfrac{1}{4}\pi,\\ \sin\theta & - \dfrac{1}{3} \sin 3\theta & & + \dfrac{1}{5} \sin 5\theta & & - \cdots = \dfrac{1}{4} \log (\sec\theta + \tan\theta)^{2} \end{alignedat} \] だと示し、級数が収束する他の全ての \(\theta\) に対する和を求めよ。
-
次を示せ: \[ \cos\theta \cos\alpha + \dfrac{1}{2} \cos 2\theta \cos 2\alpha + \dfrac{1}{3} \cos 3\theta \cos 3\alpha + \cdots = -\dfrac{1}{4} \log \{4(\cos\theta - \cos\alpha)^{2}\} \] \(\theta - \alpha\) と \(\theta + \alpha\) はどちらも \(2\pi\) の倍数でないとする。
-
\(a\) と \(b\) がどちらも実数でないとする。このとき \[ \int_{0}^{\infty} \frac{dx}{(x - a)(x - b)} = -\frac{\log(-a) - \log(-b)}{a - b} \] を示せ。二つの対数は主値を取る。正の実数 \(c\) に対する \(a = ci\) および \(b = -ci\) でこの結果を確認せよ。\(a\) と \(b\) が負の実数の場合を同様に議論せよ。
-
\(\alpha\) と \(\beta\) が実数で \(\beta \gt 0\) とする。このとき \[ \int_{0}^{\infty} \frac{d}{x^{2} - (\alpha + i\beta)^{2}} = \frac{\pi i}{2(\alpha + i\beta)} \] を示せ。\(\beta \lt 0\) なら積分の値はどうなるか?
-
\(Ax^{2} + 2Bx + C = 0\) の二つの根が符号が逆の虚部を持つとする。このとき \[ \int_{-\infty}^{\infty} \frac{dx}{Ax^{2} + 2Bx + C} = \frac{\pi i}{\sqrt{B^{2} - AC}} \] だと示せ。ここで \(\sqrt{B^{2} - AC}\) の符号は \(\{\sqrt{B^{2} - AC}\}/Ai\) の実部が正になるように選ぶ。