§34 平面上の直線に沿った変位

ここまでの二つの章で考えてきた「実数」は、様々な視点から捉えることができる。実数を幾何学的な意味を持たない純粋な数と捉えることもできるし、幾何学的な意味を持たせるにしてもその方法は少なくとも三つある。まず実数を長さの表現、つまり第一章で考えた基準直線 \(\Lambda\) に沿った長さ \(A_{0}P\) とみなす方法がある。次に実数を点の別名、つまり \(A_{0}\) からの距離が \(x\) である点 \(P\) を表すとみなす方法がある。そして実数を \(\Lambda\) 上における変位の表現つまり位置の変化量とみなす方法がある。ここでは最後の考え方についてさらに考える。

直線 \(\Lambda\) 上の点 \(P\) に置かれた小さい粒子が点 \(Q\) に移動したとする。このとき粒子を \(P\) から \(Q\) に移動させるのに必要な位置の差分あるいは位置の変動を変位 (displacement) \(\bm{\overline{PQ}}\) と呼ぶ。粒子の位置の変動を完全に記述するには、次の三つの要素が必要になる: 変位の量、直線に沿って前か後ろという変位の向き、そして変位を適用する点である。しかし粒子の移動による位置の変化だけを考えるなら、変位を適用する点を無視して、同じ長さと向きを持つ変位を同一視した方が自然である。すると変位はその長さ \(PQ = x\) と \(x\) の符号で表される向きによって完全に決定されるので、変位 \(\bm{[x]}\) と表現しても曖昧さは生じない¹ことになる。よって \(\overline{PQ} = [x]\) と書いても問題ない。

鍵括弧を使って長さおよび数字 \(x\) と変位 \([x]\) を区別する²。もし \(P\) の座標が \(a\) なら、\(Q\) の座標は \(a + x\) となる。そして変位 \([x]\) は点 \(a\) にある粒子を点 \(a + x\) まで移動させる。

次に平面上の変位を考える。直線上の変位と同様に平面上の変位 \(\overline{PQ}\) を定義するが、変位を完全に特定するために必要な情報が増える。必要な情報は四つある: (i) 変位の量、すなわち直線 \(PQ\) の長さ、(ii) 変位の方向、すなわち平面上に固定された直線と \(PQ\) がなす角度、(iii) 変位の向き、そして (iv) 適用する点である。同じ長さ・方向・向きを持つ変位を同一視するなら、もちろん四つ目は無視できる。つまり \(PQ\) と \(RS\) の長さが同じで、平行で、\(P\) から \(Q\) への運動の向きと \(R\) から \(S\) への運動の向きが同じなら、変位 \(\overline{PQ}\) と変位 \(\overline{PQ}\) は同一だとみなし、次のように表記する: \[ \overline{PQ} = \overline{RS} \]

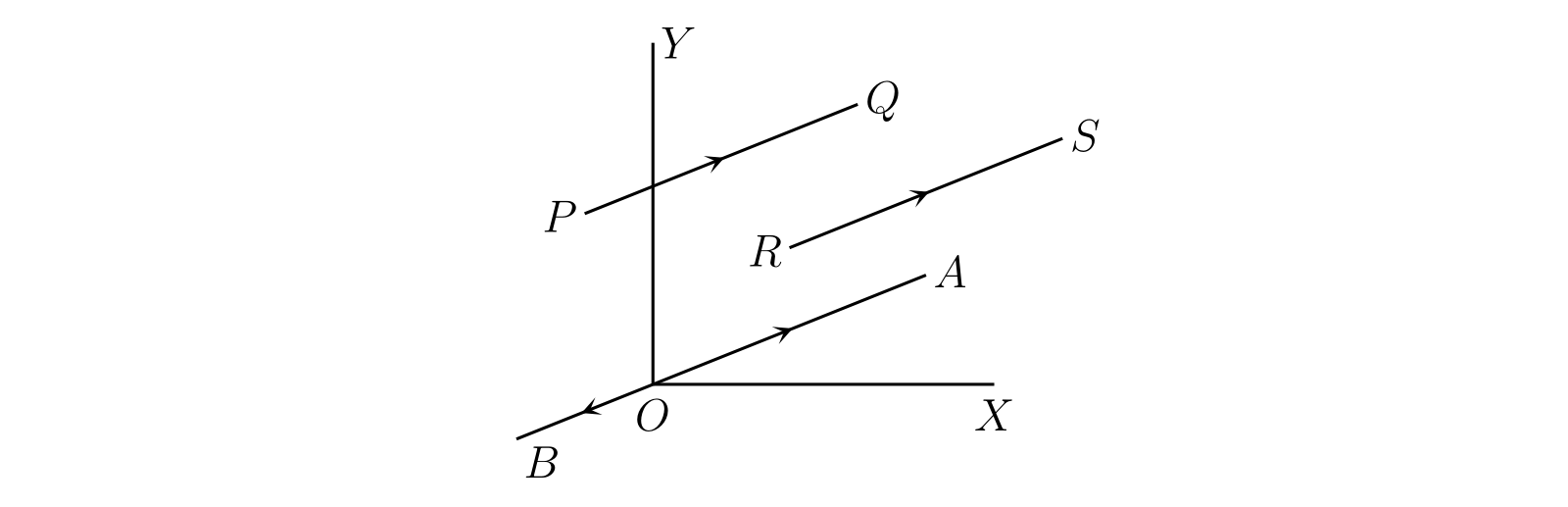
平面上に座標軸の組を (図 19 の \(OX,\ OY\) のように) 取る。\(PQ\) と同じ長さで平行な直線 \(OA\) を、\(O\) から \(A\) の向きが \(P\) から \(Q\) の向きと同じになるように取る。すると \(\overline{PQ}\) と \(\overline{OA}\) は同じ変位となる。\(x\) と \(y\) を \(A\) の座標とすると、\(\overline{OA}\) は \(x\) と \(y\) で曖昧さなく特定できる。\(\overline{OA}\) を変位 \(\bm{[x, y]}\) と呼び、次のように表記する: \[ \overline{OA} = \overline{PQ} = \overline{RS} = [x, y] \]

1. 言うまでもないが、この記号は 例 16.1 と 第二章に関するその他の例 5 で使った \([x]\) とは異なる。^[return]

2. 厳密に言えば、長さ \(x\) と長さを表す実数 \(x\) の記法も同じように区別する必要がある。そんな区別は衒学的で無駄だと思うかもしれないが、数学を学んでいけば、どんなに強く結びつくものであっても異なっているなら明確に区別しなければならないことを理解できるだろう。クリケットが数学のような科学なら、ウィケットの間のバッツマンの動き、バッツマンの獲得するラン、そしてスコアブックに記録される印を明確に区別することが非常に重要になる。^[return]