第一章 実数変数

§1 有理数

正または負の整数 \(p\) と \(q\) に対して、その比 \(r = p/q\) を有理数 (rational number) と呼ぶ。このとき \(p\) と \(q\) に公約数が存在するなら両方を公約数で割ることで、\(p\) と \(q\) が公約数を持たないと仮定できる。さらに次の等式が成り立つので、\(q\) が正だとも仮定できる: \[ \begin{aligned} \frac{p}{-q} & = \frac{-p}{q}, \quad \frac{-p}{-q} & = \frac{p}{q} \end{aligned} \] こうして定義される有理数に、\(p = 0\) とした「有理数 \(0\)」を追加する。以降はこの有理数について考える。

読者は有理数に関する基本的な算術規則を知っているものとする。次の例はそういった基本的な知識しか必要としない。

§2 数直線上の点を使った有理数の表現

数学的な解析の様々な場面において、幾何学的な図を使うと議論が分かりやすくなる。

ただし幾何学的な図を使ったとしても、解析にその図が必要なわけでは決してない。図は図に過ぎず、説明を分かりやすくするためだけに使われる。そのため、初等幾何学の概念を使った論理的な議論は必ずしも必要とならない。図が真実からどれほど離れていたとしても、図の意味することをお互いに理解できれば、それで問題ない。

直線 (straight line)・直線の線分 (segment)・線分の長さ (length) の意味を読者は知っているものとする。両方向に無限に伸びる直線 \(\Lambda\) と適当な長さを持つ線分 \(A_{0}A_{1}\) を取る。\(A_{0}\) を原点 (origin) あるいは点 \(0\)、\(A_{1}\) を点 \(1\) と呼び、この二つの点がそれぞれ数 \(0\) と \(1\) を表すとみなす。

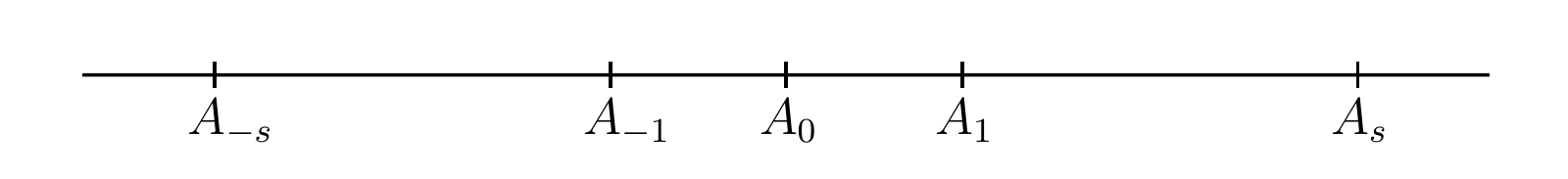
正の有理数 \(r = p/q\) を表す点を得るには、点 \(A_{r}\) を次の等式が満たされるように取る: \[ \frac{A_{0}A_{r}}{A_{0}A_{1}} = r \] ここで \(A_{0}A_{r}\) は \(A_{0}A_{1}\) と同じ方向に伸びるとする。直線を紙上に水平に書くときは、この方向を 図 1 のように左から右とする。負の有理数 \(r = -s\) を表す点を得るには、長さを符号を持つ量とみなし、ある方向 (\(A_{0}A_{1}\) の方向) に伸びるときには正を、それと反対に伸びるときには負を表すとするのが自然であり、このとき \(AB = -BA\) となる。そして \(r\) を表す点 \(A_{-s}\) は次の等式が成り立つように取る: \[ A_{0}A_{-s} = -A_{-s}A_{0} = -A_{0}A_{s} \]

ここから正と負の全ての有理数 \(r\) に対応する直線上の点 \(A_{r}\) が得られ、次式が成り立つ: \[ A_{0}A_{r} = r · A_{0}A_{1} \] \(A_{0}A_{1}\) が単位長を持つとして \(A_{0}A_{1} = 1\) とするのが自然であり、このとき \[ A_{0}A_{r} = r \] が成り立つ。有理数に対応するこの点 \(A_{r}\) を直線上の有理点 (rational points) と呼ぶ。

§3 無理数 (その 1)

分母が \(1,2,3, \ldots\) である有理数に対応する数直線上の点全てに印を付けるところを想像すれば、有理点を使って数直線上に好きなだけ細かく印を付けられることを納得できるだろう。これを正確に表現すれば「\(\Lambda\) 上に任意の線分 \(BC\) を取ると、\(BC\) 上に好きなだけ多くの有理点を見つけられる」となる。

例えば \(BC\) が線分 \(A_{1}A_{2}\) の中に含まれるとする。正の整数 \(k\) を \[ k · BC \gt 1 \qquad \text{(1)} \] が成り立つように選び¹、それから \(A_{1}A_{2}\) を \(k\) 分割すれば、その分割点のうち少なくとも一つは \(BC\) 内部にあり、さらにそれは \(B\) でも \(C\) でもない (これを \(P\) とする)。もしこうならないなら \(A_{1}A_{2}\) を \(k\) 分割した部分を \(BC\) が完全に含むが、これは仮定 \(\text(1)\) と矛盾する。よって少なくとも一つの有理点 \(P\) が \(B\) と \(C\) の間にある。しかしもしそうならば \(B\) と \(P\) の間にも有理点 \(Q\) があり、以下同様に議論できる。つまり上述の通り、有理点を好きなだけ多く見つけられる。この事実を「\(BC\) は無限に多くの (infinitely many) 有理点を含む」と表現する。

こういった考察から、数直線上の有理点だけを考えれば数直線の本質的な概念が得られると思うかもしれない。数直線が有理数のみから構成されるとみなしてその他は (もしあったとしても) 無視するのなら、もちろんこれは正しい。こうして得られる概念は直線に関する常識的な特徴の多くを持ち、直線と同じような見た目をして同じように振る舞う。

しかし考察を少し進めると、この考え方が持つ深刻な問題が明らかになる。

これからしばらくは常識的な目でこの問題を観察し、初等幾何学が扱う性質を満たす直線が当然持つはずの特徴について考える。

直線は、端点の間にある全ての点およびそれらを結んだ線分から構成されるはずである。線分はどれも長さを持ち、長さは基準あるいは単位長を使って数値として表せる量であり、加算と乗算に関する通常の代数法則を使って組み合わせられる必要がある。つまり二つの線分が与えられたときに、長さがその和または積の直線を構築できなければならない。具体的に言えば同じ直線上にある線分 \(PQ,\ QR\) の長さがそれぞれ \(a,\ b\) なら、\(PR\) の長さは \(a + b\) となる。さらに同じ直線上にある線分 \(OP,\ OQ\) の長さがそれぞれ \(1,\ a\) で、他の直線上にある線分 \(OR\) の長さが \(b\) なら、ユークリッドの構成 (Euc. vi. 12) を使って \(OP,\ OQ,\ OR\) に対する第四比例項 (fourth proportional) として長さ \(ab\) の線分 \(OS\) を構成できる必要がある。つまり \(1,\ a,\ b\) に対する代数的な第四比例項である。このように定義される和と積が次の「代数法則」に従わなければならないのは言うまでもない: \[ \begin{gathered} a + b = b + a,\quad a + (b + c) = (a + b) + c,\\ ab = ba,\quad a(bc) = (ab)c,\quad a(b + c) = ab + ac \end{gathered} \] さらに今考えている直線の長さは、等式だけではなく不等式に関する数々の自明な法則も満たす必要がある: 例えば「もし \(A,\ B,\ C\) が直線 \(\Lambda\) 上に左から右にある点なら \(AB \lt AC\)」といった法則が成り立たなくてはならない。また任意の直線上の線分と同じ長さの線分を基準となる直線 \(\Lambda\) 上に取れる必要がある。こういった直線の性質は初等幾何学の公理から要請される。

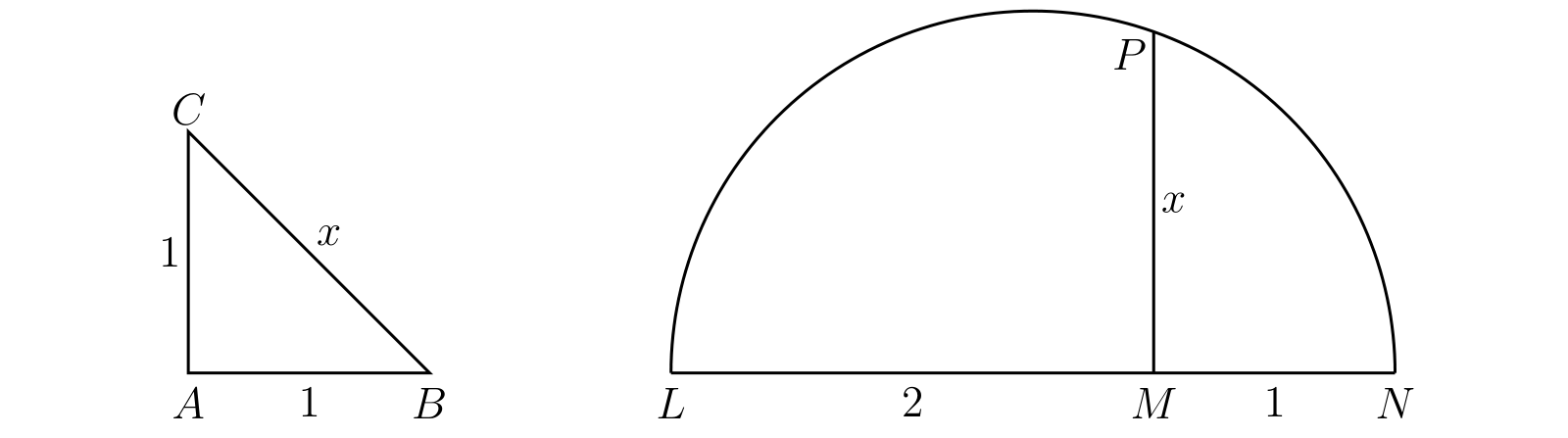
ここまでくれば、有理数に対応する点列から構成される直線の概念がこれまで述べてきた要件の全てを満たせないことが簡単に示せる。長さ \(x\) が \(x^{2} = 2\) を満たす線分を構成する幾何学的操作が存在する。例えば \(AB = AC = 1\) である垂直二等辺三角形 \(ABC\) では \(BC = x\) とすれば \(x^{2} = 2\) となる。あるいはユークリッドの構成 (Euc. vi. 13) を使って \(1\) と \(2\) の比例中項 (mean proportional) として 図 2 のように長さ \(x\) を得ることもできる。したがって先述の要件から、この数 \(x\) で表される長さ、そして次の等式を満たす \(\Lambda\) 上の点 \(P\) が存在しなければならない: \[ A_{0}P = x,\quad x^{2} = 2 \] しかし二乗すると \(\bm{2}\) になる有理数は存在しないことは容易に分かる。実を言えば、二乗すると正の既約分数 \(m/n\) になる有理数は、\(m\) と \(n\) が両方とも完全平方数でない限り存在しない。

証明は次の通り。それが可能だったとして \[ \frac{p^{2}}{q^{2}} = \frac{m}{n} \] と仮定する。ここで \(p\) と \(q\) は共通因数を持たず、\(m\) と \(n\) も共通因数を持たないとする。すると \(q^{2}\) の任意の約数は \(np^{2}\) を割り切らなければならない。\(p\) と \(q\) に共通因数がないので、\(q^{2}\) の任意の約数は \(n\) を割り切らなければならない。よって整数 \(\lambda\) を使って \(n = \lambda q^{2}\) と表せる。しかしこのとき \(m = \lambda p^{2}\) であり、\(m\) と \(n\) に共通因数がないので、\(\lambda\) は \(1\) である必要がある。したがって証明したい式 \(m = p^{2},\ n = q^{2}\) が得られる。ここに具体的な数字 \(n = 1\) を当てはめると、有理数の二乗が整数になるのはその有理数が整数である場合に限られると分かる。

つまり私たちが考えている要件には、前に構築した有理点だけではなく、\(A_{0}P = x\) かつ \(x^{2} = 2\) となる点 \(P\) と数 \(x\) が必要になる。そして初等代数で習った通り、この数 \(x\) を \(x = \sqrt{2}\) と表記する。

§4 無理数 (その 2)

有理数の幾何学的な表現を使ったここまでの議論から、新しい種類の数を追加して「数」の概念を拡張するのが望ましいことが分かった。

幾何学の言葉を使わずとも同じ結論を得ることはできる。代数における中心的な問題の一つは方程式の求解であり、例えば \[ x^{2} = 1,\quad x^{2} = 2 \] などの方程式を扱う。最初の方程式は二つの有理根 \(1\) と \(-1\) を持つが、私たちの数の概念が有理数に制限されるとすれば、二つ目の方程式には根が存在しないとしか言えなくなる。\(x^{3}=2,\ x^{4} = 7\) といった方程式も同様に解を持たなくなる。こういった方程式が解を持つことに証明が必要だと考えるなら、それだけで数の概念の拡張が望ましいと分かる。

方程式 \(x^{2} = 2\) についてさらに考える。

この方程式を満たす有理数 \(x\) は存在しないことは前に示した。任意の有理数の二乗は \(2\) より大きいか小さいかなので、有理数を二つのクラス²に分割できる: 一方のクラスには二乗が \(2\) より小さい数が含まれ、もう一方のクラスには二乗が \(2\) よりも大きい数が含まれる。ここからは正の有理数のみを考え、この二つのクラスをそれぞれ クラス \(L\) (class \(L\))、下クラス (lower class)、左手クラス (left-hand class) および クラス \(R\) (class \(R\))、上クラス (upper class)、右手クラス (right-hand class) と呼ぶ。明らかに、\(R\) に属する任意の数は \(L\) に属する全ての数より大きい。またクラス \(L\) に属する数であって二乗が \(2\) より小さいものの \(2\) に好きなだけ近いものを見つけられること、そしてクラス \(R\) に属する数であって二乗が \(2\) より大きいものの \(2\) に好きなだけ近いものを見つけられることは容易に納得できる。実際、\(2\) を開平する通常の算術処理を行えば、二乗が \(2\) に限りなく近づいていく有理数の列を得られる。つまり \[ 1,\quad 1.4,\quad 1.41,\quad 1.414,\quad 1.4142,\quad \ldots \] の二乗 \[ 1,\quad 1.96, \quad 1.9881, \quad 1.999396,\quad 1.99996164,\quad \ldots \] は全て \(2\) より小さいが、限りなく \(2\) に接近する。桁数を十分多く取れば、望むだけ正確な近似を得られる。そしてこの近似の最後の桁をそれぞれ \(1\) 増やせば、有理数の数列 \[ 2,\quad 1.5,\quad 1.42,\quad 1.415,\quad 1.4143,\quad \ldots \] が得られる。この二乗 \[ 4,\quad 2.25,\quad 2.0164,\quad 2.002225,\quad 2.00024449,\quad \ldots \] は全て \(2\) より大きく、\(2\) に好きなだけ接近する。

ここから「\(L\) の最大要素と \(R\) の最小要素は存在しない」ことも分かる: \(L\) の任意の要素 \(x\) に対して \(x^{2} \lt 2\) が成り立つので、\(x^{2} = 2 - \delta\) とすれば \(L\) の要素 \(x_{1}\) であって \(x_{1}^{2}\) と \(2\) の差が \(\delta\) 未満であるものを取れる。このとき \(x_{1}^{2} \gt x^{2}\) すなわち \(x_{1} \gt x\) である。よって \(L\) には \(x\) より大きい要素がある。\(x\) は \(L\) の任意の要素だったから、\(L\) には他の全ての要素よりも大きい要素が存在しないことが言える。よって \(L\) は最大要素を持たず、同様に \(R\) は最小要素を持たない。

§5 無理数 (その 3)

前節では正の有理数を二つのクラス \(L\) と \(R\) に分割した。このとき (i) \(R\) の全ての要素は \(L\) のどんな要素よりもより大きく、(ii) \(L\) の要素と \(R\) の要素の組であって差が好きなだけ小さいものを取ることができ、(iii) \(L\) は最大要素を持たず、\(R\) は最小要素を持たない。直線の常識的な性質や初等幾何と初等代数からの要請といったものを考えると、\(\bm{L}\) の全ての要素よりも大きく \(\bm{R}\) の全ての要素よりも小さい数 \(\bm{x}\)、および \(\bm{L}\) に対応する点と \(\bm{R}\) に対応する点を分ける \(\bm{\Lambda}\) 上の点 \(\bm{P}\) の存在が必要となる。

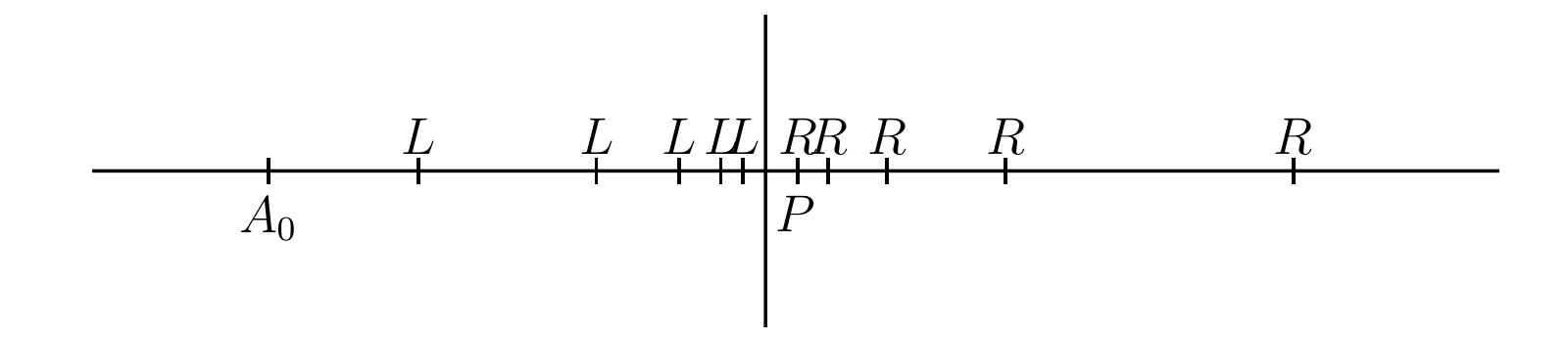
そのような数 \(x\) が存在して代数法則に従うと一時的に仮定する。この仮定の下では例えば \(x^{2}\) が明確な意味を持ち、\(x^{2}\) は \(2\) とちょうど等しい。もし \(x^{2}\) が \(2\) よりも小さいとすると、前節の議論から有理数 \(\xi\) であって \(\xi^{2}\) が \(x^{2}\) と \(2\) の間にあるものが存在する、つまり \(x\) よりも大きい \(L\) の要素を見つけられるが、これは \(x\) が \(L\) と \(R\) の要素を分けるという仮定と矛盾する。したがって \(x^{2}\) は \(2\) より小さくなりえず、同様に \(2\) よりも大きくなりえない。よって \(x^{2} = 2\) と結論でき、代数ではこの数 \(x\) を \(\sqrt{2}\) と表記する。二乗して \(2\) になる有理数は存在しないので、もちろん \(\sqrt{2}\) は有理数でない。\(\sqrt{2}\) は無理数 (irrational number) の一番単純な例である。

以上の議論は \(x^{2} = 2\) 以外の方程式にもそのまま適用できる。例えば完全平方数でない自然数 \(N\) についての \(x^{2} = N\)、あるいは \[ x^{3} = 3,\quad x^{3} = 7,\quad x^{4} = 23 \] といった方程式、さらに後述するように \(x^{3} = 3x + 8\) のような方程式にも適用できる。そのためこういった方程式を満たす無理数 \(x\) やそれに対応する \(\Lambda\) 上の点 \(P\) の存在も私たちは信じることになる。こういった長さは (\(\sqrt{2}\) と違って) 初等幾何学の方法で構成できないにもかかわらずである。

読者は他の講義も受けているかもしれない。もし望むなら、\(\sqrt{2}\) や \(\sqrt[3]{3}\) といった「無理数」が存在して、読者もよく知っているであろう代数法則も成り立つものだと仮定してしまってもよい³。もしそうするなら、次の節からの抽象的な議論を飛ばして §13 まで進んで構わない。

一方でそのような素朴な態度を取る気にならないのであれば、こういった問題をより詳しく議論する以降の節を注意深く読むよう強く勧める⁴。

§6 無理数 (その 4)

§4 では正の有理数 \(x\) を二つのクラスに分割する具体的な方法を説明し、\(x^{2} \lt 2\) を満たすクラスと \(x^{2} \gt 2\) を満たすクラスを考えた。この分割方法を、考えている数の切断 (section) と呼ぶ。二つのクラスの要素を特徴付ける不等式が \(x^{3} \lt 2\) と \(x^{3} \gt 2\)、あるいは \(x^{4} \lt 7\) と \(x^{4} \gt 7\) である場合にも切断を同じように構成できる。こういった正の有理数の「切断」の構築に関するごく自然な法則を示そう。

\(P\) と \(Q\) をとある性質とし、ある正の有理数が両方を同時に満たすことはなく、全ての正の有理数はどちらかを必ず満たすとする。さらに \(P\) を満たす全ての数は \(Q\) を満たすどんな数よりも小さいと仮定する。例えば \(P\) が「\(x^{2} \lt 2\)」という性質で \(Q\) が「\(x^{2} \gt 2\)」という性質かもしれない。このとき \(P\) を満たす数の集まりを下クラス (lower class) あるいは左手クラス (left-hand class) \(L\) と呼び、\(Q\) を満たす数の集まりを上クラス (upper class) あるいは右手クラス (right-hand class) \(R\) と呼ぶ。通常はどちらのクラスも存在するが、一方が要素を持たず、もう片方に全ての有理数が属することも特殊ケースとしてあり得る。例えば \(P\) (あるいは \(Q\)) を「有理数である」や「正である」とすると明らかにこの状況になる。しかし今は、二つのクラスの要素が存在するとして話を進める。このとき §4 で示したように、\(L\) の要素と \(R\) の要素の組でその差が好きなだけ小さいものを見つけられる。

§4 で考えた特殊ケースでは \(L\) は最大要素を持たず、\(R\) は最小要素を持たなかった。二つのクラスの最大要素と最小要素に関するこの問題は非常に重要である。まず、\(L\) が最大要素を持ってかつ \(R\) が最小要素を持つことはあり得ない。もし \(l\) が \(L\) の最大要素で \(r\) が \(R\) の最小要素なら \(l \lt r\) であり、このとき \(\frac{1}{2}(l + r)\) が \(l\) と \(r\) の間にある正の有理数となり、これは \(L\) にも \(R\) にも属さない。しかしこれは全ての正の有理数がどちらかのクラスに属するという仮定と矛盾する。よって可能性は三つある: (i) \(L\) に最大要素 \(l\) がある (ii) \(R\) に最小要素 \(r\) がある (iii) \(L\) の最大要素も \(R\) の最小要素も存在しない。これらが同時に複数起こることはない。

§7 無理数 (その 5)

前節の最後で示した最初の二つのケースでは、切断が正の有理数 \(a\) に対応する。最初のケースでは \(a = l\) で、もう一つでは \(a = r\) となる。逆に正の有理数 \(a\) がある切断に対応するのも明らかなので、その切断を \(\alpha\) と表記する⁵。例えば \(P\) と \(Q\) がそれぞれ \[ x \leq a,\quad x \gt a \] という不等式、あるいは \(x \lt a\) と \(x \geq a\) という不等式で表されるケースがこれにあたる。最初のケースでは \(a\) が \(L\) の最大要素となり、二つ目のケースでは \(a\) が \(R\) の最小要素となる。実は正の有理数に対応する切断はこの二つしかない。そこで曖昧さをなくすために、一つを選んでおく: 私たちは考えている数字が上クラスに属するケースを選ぶ。言い換えると、以降は \(L\) が最大要素を持たない切断だけを考えることにする。

正の有理数とそれを使って定義される切断の間にこういった対応関係が存在するので、数学的な議論においては、正の有理数と切断を取り換えて、式に出てくる記号が有理数でなくて切断を表しているとみなしても何ら不都合は生じない。例えば \(a, a'\) に対応する切断が \(\alpha, \alpha'\) なら、「\(\alpha \gt \alpha'\)」と「\(a \gt a'\)」が同じ意味を持っているとしても構わない。

しかしこうして正の有理数とそれに対応する切断を取り換えるとすると、私たちが考えてきた数体系の拡張がほぼ強制される。切断には (§4 で見たように) 有理数に対応しない切断も存在するのである。切断を全て集めると、そこには有理数に対応する切断以外のものが含まれ、有理数を集めたものより大きくなる。この事実は、私たちが数の概念を拡張するときの基礎となる。ただし次の節で変更するので、一時的な仮のものに過ぎない:

§8 実数

前節では正の有理数の切断に話を限定し、この切断を仮に「正の実数」と呼んだ。最終的な定義を述べるには、これまでの定義を少し変える必要がある。ここからは切断、すなわち二つのクラスへの分割を、正の有理数だけではなく \(0\) を含めた全ての有理数に対して考えることにする。このとき §6–§7 で正の有理数の切断について行った議論は、「正の」という言葉を適切に省略すればもう一度行える。そして次のように実数を定義する:

もし実数が有理数に対応するなら、その実数に対しても有理数 (rational number) という言葉を使うことにする。

区別すべきケースが三つある。まず全ての負の有理数が下のクラスに属し、\(0\) と全ての正の有理数が上のクラスに属する場合がある。この切断を実数 \(\bm{0}\) (real number zero) と呼ぶ。次に下のクラスが正の有理数を含む場合がある。そのような切断は正の実数 (positive real number) と呼ぶ。最後に上のクラスが負の有理数を含む場合がある。そのような切断は負の実数 (negative real number) と呼ぶ⁶。

§9 実数の大きさの関係

数の概念を拡張して次に当然行うべきは、対応する等号・不等号・加算・乗算といった概念の拡張である。こういった概念を新しい数に適用する方法、そして拡張された概念が通常の代数法則を満たすことを示す必要がある。この証明がなくては、一般的な実数を §1 の有理数と同じように扱えない。しかし全てを詳細に示すには多くの紙面が必要になるので、ここでは詳細な議論の進め方を大まかに示すに留める。

実数は \(\alpha,\ \beta,\ \gamma,\ \ldots\) といったギリシャ文字で表し、対応する下のクラスと上のクラスに属する有理数をそれぞれ \(a\) と \(A\)、\(b\) と \(B\)、\(c\) と \(C\) と言ったアルファベットで表す。クラス自身は \((a),\ (A)\) などで表す。

二つの実数 \(\alpha\) と \(\beta\) の関係には三つの可能性がある:

1. 全ての \(a\) が \(b\) であり、全ての \(A\) が \(B\) である。このとき \((a)\) と \((b)\) および \((A)\) と \((B)\) は同一となる。
2. 全ての \(a\) は \(b\) であるが、\(A\) の全ては \(B\) でない。このとき \((a)\) は \((b)\) の真の部分⁷となり、かつ \((B)\) は \((A)\) の真の部分となる。
3. 全ての \(A\) は \(B\) だが、\(a\) の全ては \(b\) でない。

この三つの場合を 図 4 に図示する。

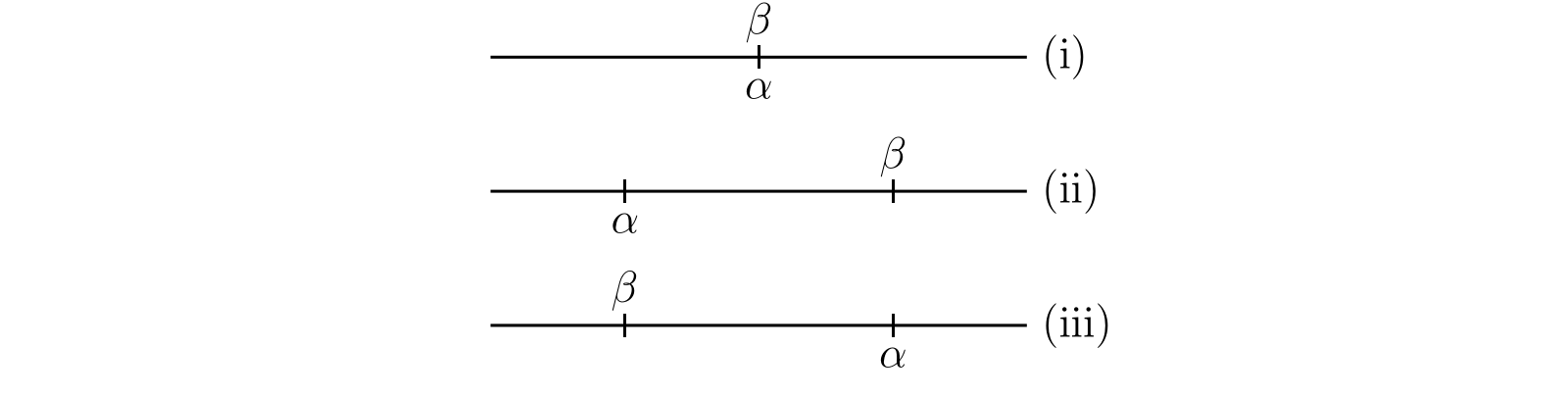
(i) のとき \(\alpha = \beta\) と表記し、(ii) のときは \(\alpha \lt \beta\) と、(iii) のときは \(\alpha \gt \beta\) と表記する。\(\alpha\) と \(\beta\) が共に有理数のとき、私たちが知っているとみなしていた有理数に関する等式と不等式がこの定義と矛盾しないことは明らかである。また任意の正の数が任意の負の数より大きいことも容易に分かる。

この段階で正の数 \(\alpha\) に対する負の数 \(-\alpha\) 定義すると便利だろう。\((a),\ (A)\) を \(\alpha\) に対応するクラスとして、下のクラスに全ての \(-A\) を、上のクラスに全ての \(-a\) を取ると新たな切断を定義できる。こうして定義される実数を \(-\alpha\) と表す。\(-\alpha\) は明らかに負となる。同様に \(\alpha\) が負または \(0\) のときにも \(-\alpha\) を定義できる。\(\alpha\) が負ならば \(-\alpha\) は正となり、\(-(-\alpha) = \alpha\) なことは容易に分かる。\(\alpha\) と \(-\alpha\) のうち一方が正となる (\(\alpha = 0\) の場合は除く) が、二つのうち正の方を \(|\alpha|\) と表記し、\(\alpha\) の絶対値 (absolute value) あるいは大きさ (modulus) と呼ぶ。

[以上の結果は全て定義から直ちに得られる]

§10 実数に対する代数演算 (その 1)

続いて、加算などの初等的な代数演算を実数に対して一般的に定義する。

1. 加算: 二つの数 \(\alpha\) と \(\beta\) の和の定義では、全ての和 \(c = a + b\) から得られる \((c)\) と全ての和 \(C = A + B\) から得られる \((C)\) という二つのクラスを考える。明らかに \(c \lt C\) が常に成り立つ。

   ここでも、\(c\) にも \(C\) にも属さない有理数は最大でも一つである。もしそのような二つの有理数 \(r,\ s\) が存在して \(s\) の方が大きかったとすると、\(r\) と \(s\) の両方は任意の \(c\) より大きく任意の \(C\) より小さい。よって \(C - c\) が \(s - r\) より大きくなる。一方で \[ C - c = (A - a) + (B - b) \] であり、\(a,\ b,\ A,\ B\) は \(A - a\) と \(B - b\) が好きなだけ小さくなるように取れる。これは明らかに仮定と矛盾する。

   もし全ての有理数が \((c)\) または \((C)\) に属するなら、\((c)\) と \((C)\) という二つのクラスが有理数の切断、つまり実数 \(\gamma\) を構成する。もし二つのクラスに属さない有理数があるなら、\((C)\) に加える。このとき手に入る切断すなわち実数 \(\gamma\) は \((C)\) の最小要素に対応するので、明らかに有理数となる。いずれの場合でも \(\gamma\) を \(\alpha\) と \(\beta\) の和 (sum) と呼び、 \[ \gamma = \alpha + \beta \] と表記する。

   もし \(\alpha\) と \(\beta\) の両方が有理数なら、上クラス \((A)\) と \((B)\) に最小要素が存在する。このとき \(\alpha + \beta\) が \((C)\) の最小要素となり、結果がこれまでの加算の概念と一致する。

2. 減算: \(\alpha - \beta\) を次のように定義する: \[ \alpha - \beta = \alpha + (-\beta) \] この減算の定義から生まれる新たな困難はない。

§11 実数に対する代数演算 (その 2)

3. 乗算: 乗算では最初に (\(0\) を含んだ) 正の数だけを考え、§4–§7 で扱った正の有理数からなる切断に戻ると簡単になる。\((c)\) を \((ab)\)、\((C)\) を \((AB)\) とすれば加算と本質的に同じ道をたどれる。議論が唯一異なるのが、最大でも一つの例外を除いた全ての有理数が \(c\) または \(C\) に属することを示す部分である。\(a,\ A,\ b,\ B\) を \(C - c\) が好きなだけ小さくなるように選べることを示すこの部分では、次の等式を使う: \[ C - c = AB - ab = (A - a)B + a(B - b) \] そして負の数を定義に含めるために、正の数 \(\alpha\) と \(\beta\) に対して次のように定義する: \[ (-\alpha)\beta = -\alpha\beta,\quad \alpha(-\beta) = -\alpha\beta,\quad (-\alpha)(-\beta) = \alpha\beta \]

4. 除算: 除算の定義は (\(0\) 以外の) 数 \(\alpha\) に対する逆数 \(1/\alpha\) の定義からはじめる。最初は正の数と正の有理数の切断だけを考え、正の数 \(\alpha\) の逆数を下クラス \((1/A)\) と 上クラス \((1/a)\) を使って定義する。そして負の数 \(-\alpha\) の逆数を \(1/(-\alpha) = -(1/\alpha)\) と定義し、\(\alpha/\beta\) を次のように定義する: \[ \alpha/\beta = \alpha × (1/\beta) \]

ここまでくれば、初等代数における概念や操作の全てを有理数と無理数の実数全てに対して適用できる。ただしこの処理を詳細に示すことはしない。特に重要で特殊な一部の無理数クラスに注意を向けた方が面白いし、得るものも多いだろう。

§12 実数 \(\sqrt{2}\)

前に §4–§5 で個別に考えた無理数に戻ろう。そこでは不等式 \(x^{2} \lt 2\) と \(x^{2} \gt 2\) を使って切断を構築した。この切断はもともと正の有理数だけからなっていたが、後に (§8 で) 全ての有理数からなる切断に置き換えた。こうして定義される切断あるいは実数は \(\sqrt{2}\) と表記される。

\(\sqrt{2}\) とそれ自身の積として構築されるクラスは、(i) 二乗が \(2\) より小さい正の有理数 \(a,\ a'\) に対する \((aa')\)、および (ii) 二乗が \(2\) より大きい正の有理数 \(A,\ A'\) に対する \((AA')\) からなる。これらのクラスは \(2\) 以外の全ての正の有理数を含むので、 \[ (\sqrt{2})^{2} = \sqrt{2}\sqrt{2} = 2 \]

が成り立つ。加えて \[ (-\sqrt{2})^{2} = (-\sqrt{2})(-\sqrt{2}) = \sqrt{2}\sqrt{2} = (\sqrt{2})^{2} = 2 \] も成り立つので、方程式 \(\bm{x^{2} = 2}\) には \(\bm{\sqrt{2}}\) と \(-\bm{\sqrt{2}}\) という二つの根がある。同じ議論は \(x^{2} = 3,\ x^{3} = 7,\ \ldots\) といった方程式に対応する \(\sqrt{3},\ -\sqrt{3},\ \sqrt[3]{7},\ \ldots\) に対しても同様に行える。

§13 二次の不尽根数

有理数の二乗でない正の有理数 \(a\) に対して、\(±\sqrt{a}\) の形をした実数を純粋な二次の不尽根数 (pure quadratic surd) と呼ぶ。有理数 \(a\) と純粋な二次の不尽根数 \(\sqrt{b}\) に対して、\(a ± \sqrt{b}\) の形をした数を混ざった二次の不尽根数 (mixed quadratic surd) と呼ぶことがある。

§3 に示した幾何学的な考察によって存在が示される無理数は、純粋な二次の不尽根数、混ざった二次の不尽根数、そして二乗根を何度か使って表せる入り組んだ無理数に限られる。最後の例としては次の数がある: \[ \sqrt{2} + \sqrt{2 + \sqrt{2}} + \sqrt{2 + \sqrt{2 + \sqrt{2}}} \]

こういった形をした数と同じ長さの線分の幾何学的な構築は簡単に行える。読者はすぐに自分でできるだろう。ユークリッドの方法 (定規とコンパスを使った幾何学的な作図) で構築できるのがこの形の無理数に限られるのは重要な事実である (が、その証明は今は示さない。第二章に関するその他の例を参照)。この特徴により、二次の不尽根数は非常に興味深い数となる。

§14 二次の不尽根数に関する諸定理

二つの純粋な二次の不尽根数が同じ不尽根数の有理数倍として表せるなら、二つは相似 (similar) であると言う。そうでないなら非相似 (dissimiar) と言う。例えば \[ \sqrt{8} = 2\sqrt{2},\quad \sqrt{\frac{25}{2}} = \frac{5}{2}\sqrt{2} \] だから、二つの純粋な不尽根数 \(\sqrt{8}\) と \(\sqrt{\frac{25}{2}}\) は相似だと分かる。一方 \(M\) と \(N\) が共通約数を持たない整数であって両方とも完全平方数でないなら、\(\sqrt{M}\) と \(\sqrt{N}\) は非相似である。証明は次の通り。もし相似なら \[ \sqrt{M} = \frac{p}{q}\sqrt{\frac{t}{u}},\quad \sqrt{N} = \frac{r}{s}\sqrt{\frac{t}{u}} \] となる。ここで \(p,q,r,s,t,u\) は全て整数である。

このとき \(\sqrt{MN}\) は有理数であり、さらに 例 2.3 より整数となる。よってある整数 \(P^{2}\) があって \(MN=P^{2}\) となる。\(P\) の因数を \(a,\ b,\ c,\ \ldots\) とすれば \[ MN = a^{2\alpha} b^{2\beta} c^{2\gamma}\ \ldots \] と表せる (\(\alpha,\ \beta,\ \gamma,\ \ldots\) は正の整数)。このとき \(MN\) は \(a^{2\alpha}\) で割り切れ、次のどれかが成り立つ: (i) \(M\) が \(a^{2\alpha}\) で割り切れる (ii) \(N\) が \(a^{2\alpha}\) で割り切れる (iii) \(M\) と \(N\) の両方が \(a\) で割り切れる。\(M\) と \(N\) は共通因数を持たないので、最後のケースはあり得ない。この議論は全ての因数 \(a^{2\alpha},\ b^{2\beta},\ c^{2\gamma},\ \ldots\) に対して行えるので、\(M\) はこの因数のいくつかで割り切れ、\(N\) はそれ以外の因数で割り切れる。よって \[ M = P_{1}^{2},\quad N = P_{2}^{2} \] となる。ここで \(P_{1}^{2}\) は \(a^{2\alpha},\ b^{2\beta},\ c^{2\gamma},\ \ldots\) のいずれかの積で、\(P_{2}^{2}\) はそれ以外の積である。したがって \(M\) と \(N\) は両方とも完全平方数となるが、これは仮定と矛盾する。

証明を示す。仮定から \(B - D\) と \[ \sqrt{B} - \sqrt{D} = C - A \] がどちらも有理数と分かる。\(B\) が \(D\) と等しくないなら \[ \sqrt{B} + \sqrt{D} = \frac{B - D}{\sqrt{B}- \sqrt{D}} \] も有理数となり、よって \(\sqrt{B}\) と \(\sqrt{D}\) も有理数となる (\(B\) と \(D\) が等しいとき \(A\) と \(C\) が等しいのは明らかに分かる)。

§15 連続体

全ての実数 (有理数と無理数) の集まりを算術的連続体 (arithmetical continuum) と呼ぶ。

§2 の直線 \(\Lambda\) が算術的連続体に含まれる数に対応する点のみからなる¹¹と考えると理解しやすい。線形連続体 (linear continuum) と呼ばれるこの直線上の点の集合は、算術的連続体の分かりやすいイメージとなる。

ここまではいくらかの時間をかけて、いくつかの実数のクラス、例えば有理数や二次の不尽根数が持つ重要な特徴を見てきた。ここでさらに例を示して、そういった非常に特別な個別のクラスが、算術的連続体を構成する無限に多くの数の (大雑把に言って) ほんの一部でしかないことを示す。

1. 不尽根数を使ったこれまでよりも複雑な次の式を考える: \[ z = \sqrt[3]{4 + \sqrt{15}} + \sqrt[3]{4 - \sqrt{15}} \] \(z\) を表すこの式が意味を持つことの議論の一例を示す。まず §12 と同様に \(y^{2} = 15\) を満たす数 \(y = \sqrt{15}\) が存在することが示せる。そうすれば §10 と同様に \(4 + \sqrt{15},\ 4 - \sqrt{15}\) を定義できるので、続いて \(z_{1}\) に関する次の方程式を考える: \[ z_{1}^{3} = 4 + \sqrt{15} \] この方程式の右辺は有理数でない。しかし \(x^{3} = 2\) (あるいは他の有理数) を満たす実数 \(x\) が存在するのと同じ議論で、\(z_{1}^{3} = 4 + \sqrt{15}\) を満たす数 \(z_{1}\) が存在すると結論できる。そうすれば \(z_{1} = \sqrt[3]{4 + \sqrt{15}}\) および \(z_{2} = \sqrt[3]{4 - \sqrt{15}}\) を定義でき、§10 と同様にして \(z = z_{1} + z_{2}\) を定義できる。

   また \(z\) が与えられれば、次の等式¹²が成り立つかどうかは簡単に確認できる: \[ z^{3} = 3z + 8 \] この事実を使えば、\(z^{3} = 3z + 8\) を満たす実数 \(z\) がただ一つ存在することを直接的に証明できる。まず、そのような数が二つは存在しないことは容易に分かる。もし \(z_{1}^{3} = 3z_{1} + 8\) かつ \(z_{2}^{3} = 3z_{2} + 8\) だとすれば、両辺を引いて \(z_{1} - z_{2}\) で割ると \(z_{1}^{2} + z_{1}z_{2} + z_{2}^{2} = 3\) となる。さらにもし \(z_{1}\) と \(z_{2}\) が正であれば \(z_{1}^{3}\gt8\) かつ \(z_{2}^{3}\gt8\) であり、したがって \(z_{1} \gt 2,\ z_{2} \gt 2,\ z_{1}^{2} + z_{1}z_{2} + z_{2}^{2} \gt 12\) が分かる。つまり方程式は満たされない。さらに \(z_{1}\) と \(z_{2}\) が負でないのも容易に示せる。もし \(z_{1}\) が負で \(-\zeta\) だったとすると、\(\zeta\) は正であり \(\zeta^{3} - 3\zeta + 8 = 0\) すなわち \(3 - \zeta^{2} = 8/\zeta\) が成り立つ。よって \(3 - \zeta^{2} \gt 0\) となって \(\zeta \lt 2\) が分かる。しかしこのとき \(8/\zeta \gt 4\) であり、\(8/\zeta\) は \(3\) より小さい \(3 - \zeta^{2}\) と等しくならない。

   よって \(z^{3} = 3z + 8\) を満たす \(z\) は多くとも一つしかない。さらに \(z\) が有理数でないことも分かる。この方程式の有理根は整数かつ \(8\) の因数でなければならず (例 2.3)、\(1,\ 2,\ 4,\ 8\) がどれも根でないのはすぐに確認できるからである。

   以上より \(z^{3} = 3z + 8\) は多くとも一つの根を持ち、根が存在するならそれは正であり有理数でないことが分かる。有理数 \(x\) を \(x^{3} \lt 3x + 8\) であるものと \(x^{3} \gt 3x + 8\) であるものに分割して \(L,\ R\) とする。\(x^{3} \gt 3x + 8\) ならば \(x\) より大きい任意の \(y\) も \(y^{3} \gt 3y + 8\) を満たすのは明らかである。仮に \(y^{3} \leq 3y + 8\) だとすると、\(x^{3} \gt 3x + 8\) と両辺を引けば \(y^{3} - x^{3} \lt 3(y - x)\) すなわち \(y^{2} + xy + x^{2} \lt 3\) となるが、\(y\) が正で (\(x^{3} \gt 8\) から) \(x \gt 2\) なのでこれはあり得ない。同様にして \(x^{3} \lt 2x + 8\) かつ \(y \lt x\) ならば \(y^{3} \lt 3y + 8\) が分かる。

   最後に、\(L\) と \(R\) がどちらも存在することは容易に示せる。そして \(L\) と \(R\) が構成するのは正の有理数の切断、すなわち方程式 \(z^{3} = 3z + 8\) を満たす実数 \(z\) である。あるいはカルダノの方法を使った三次方程式の解法を使えば、方程式から直接 \(z\) の明示的な式を得られる。

2. 方程式 \(x^{3} = 3x + 8\) に用いた上記の直接的な議論は (多少難しくはなるが) 次の方程式にも適用できる: \[ x^{5} = x + 16 \] その結果として、この方程式を満たす単一の正の実数の存在が結論できる。ただしこの場合には、不尽根数の組み合わせからなる \(x\) の単純な表現を得ることはできない。実は、次数が \(4\) より大きい方程式の根に対するそういった表現を一般的に見つけるのは不可能であることが示されている (ただし証明は難しい)。そのため、純粋な二次の不尽根数、混ざった二次の不尽根数、その他の不尽根数、およびそれらを組み合わせてできる実数の他にも、代数方程式の根であるがそういった形に表現できない数が存在する。実数に対してこういった不尽根数を使った表現が見つかるのは非常に特殊な場合に限られる。

3. しかし、私たちが考えてきた無理数のリストに方程式 (\(x^{5} = x + 16\) など) の不尽根数でない根を加えたとしても、そのリストが算術的連続体に含まれる無理数を全て含むわけではない。直径が \(A_{0}A_{1}\) (単位直線) の円を描いたとき、その円周の長さを数値として表せると考えるのが自然である¹³。通常 \(\pi\) と表されるこの長さは、整数係数代数方程式の根でないことが証明されている¹⁴ (残念ながら証明は長く、難しい)。整数係数代数方程式とは例えば \[ \pi^{2} = n,\quad \pi^{3} = n,\quad \pi^{5} = \pi + n \] である (\(n\) は整数)。こういった方法を使うと、これまでに考えたどの無理数のクラスにも属さず有理数でもない数を定義できる。この \(\pi\) という数は独立した特殊ケースではなく、これ以外の例もいくらでも構築できる。実際、整数係数の代数方程式の根である無理数は特殊なクラスに過ぎず、不尽根数を使って表せる数はそれに含まれるさらに小さいクラスである。

§16 連続な実数変数

「実数」を捉える二つの異なる視点がある。一つは実数を前節で定義した「算術的連続体」という集まりだと考え、もう一つは実数を個別に考える。実数を個別に考えるときは特定の指定された数 (例えば \(1,\ -\frac{1}{2},\ \sqrt{2},\ \pi\)) を念頭に置く場合もあれば、任意の数・不詳の数・とある数 \(x\) を念頭に置く場合もある。後者の考え方をするのは、私たちが「\(x\) は数だ」「\(x\) は長さの単位だ」「\(x\) は有理数でも無理数でもあり得る」などと言った場合である。こういった命題における \(x\) は連続実数変数 (continuous real variable) と呼ばれ、個別の実数は変数の値 (value) と呼ばれる。

連続でない「変数」もある。全ての実数の集まりではなく、それに含まれる部分的な集まり、例えば有理数の集まりや正の整数の集まりを考える場合がこれに当たる。例えば正の整数の集まりが登場する例としては、任意の (不詳の) 正の整数に関する「\(n\) は奇数または偶数だ」のような文がある。ここでは \(n\) が変数、それも正の整数変数になり、個別の正の整数がその値となる。

当然この \(x\) や \(n\) は変数の例に過ぎない。「変動領域 (field of variation)」が実数および正の整数であるこの二つの例は最も重要なものだが、他の変数を考えることもある。例えば十進数を議論するときには、十進数で表した数の各桁の値を \(x\) を使って表すかもしれない。このとき \(x\) は変数だが、\(0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9\) の十個しか異なる値を取らない。読者はこれ以外にも様々な変動領域を持つ変数の例を見つけられるだろう: 警察官 \(x\)・タクシー運転手 \(x\)・年 \(x\)・週の \(x\) 日目など、数字でない値を持つ変数もある。

§17 実数の切断 (デデキントの定理)

§4–§7 では有理数の「切断」、すなわち (正の) 有理数を二つのクラス \(L\) と \(R\) に分割する方法について考えた。\(L\) と \(R\) には次の性質がある:

1. 考えている数全てが、二つのクラスのどちらか一方に属する。
2. 両方のクラスが要素を持つ。
3. \(L\) に属する任意の数は \(R\) に属する任意の数より小さい。

もちろん、全ての実数の集まりにもこの考えを適用できる。この考え方が非常に重要なことが後の章で分かる。

\(P\) と \(Q\) を互いに矛盾する実数に関する性質と仮定し¹⁵、全ての実数が \(P\) と \(Q\) のどちらかを持つとする。さらに \(P\) を満たす任意の数は \(Q\) を満たす任意の数より小さいとする。このとき \(P\) を 下クラス (lower class) あるいは 左手クラス (left-hand class) \(L\) と呼び、\(Q\) を 上クラス (upper class) あるいは 右手クラス (right-hand class) \(R\) と呼ぶ。

このとき二つの可能性がある¹⁶。\(L\) が最大要素 \(l\) を持つか、\(R\) が最小要素 \(r\) を持つかである。両方が起こることはない。もし \(L\) の最大要素 \(l\) と \(R\) の最小要素 \(r\) が存在するなら、\(\frac{1}{2}(l + r)\) という数が \(L\) に属する全ての数より大きく \(R\) に属する全ての数より小さくなり、どちらのクラスにも属さなくなる。一方で二つの可能性の片方は必ず成り立つ¹⁷。

\(L_{1}\) と \(R_{1}\) を、\(L\) と \(R\) に属する有理数だけを取ってできるクラスとする。このとき \(L_{1}\) と \(R_{1}\) というクラスの組は有理数の切断を構成する。分けて考えるべきケースが二つある。

まず \(L_{1}\) が最大要素 \(\alpha\) を持つ可能性がある。このとき \(\alpha\) は \(L\) の最大要素でもある。もしそうでないとすると、\(\alpha\) よりも大きい数 \(\beta\) が \(L\) に属する。すると \(\alpha\) と \(\beta\) の間にある (\(\beta\) より小さい) 有理数も \(L\) に属することになり、その有理数は \(L_{1}\) にも属するが、これは仮定と矛盾する。したがって \(\alpha\) は \(L\) の最大要素となる。

一方で \(L_{1}\) が最大要素を持たない場合もある。このとき \(L_{1}\) と \(R_{1}\) という有理数の切断は実数 \(\alpha\) となる。この \(\alpha\) は \(L\) と \(R\) のどちらかに属する。もし \(\alpha\) が \(L\) に属するなら、前段落と同様にそれが \(L\) の最大要素だと示せる。もし \(\alpha\) が \(R\) に属するなら同じようにそれが \(R\) の最小要素となる。

よっていずれの場合でも、\(L\) が最大要素を持つか \(R\) が最小要素を持つかのどちらかとなる。つまり任意の実数の切断はとある実数に「対応」する。これは有理数の切断が有理数に対応するのと同様だが、有理数では切断が有理数に対応しない場合もあった。この結論は非常に重要である。なぜならこの結論は、全ての実数の切断を考えたとしても数の概念をさらに拡張する必要がないことを示すからである。有理数の切断を考えると有理数から実数というより一般的な新しい数の概念が導かれると私たちは発見した。それなら実数の切断を考えればさらに一般的な概念を得られると期待するかもしれない。しかしこれまでの議論はそれが起こらないことを示す。実数の集まり、またの名を算術的連続体には、有理数の集まりにはないある種の完全性がある。この完全性を専門用語で「算術的連続体は閉である」と表現する。

今ちょうど証明したこの結論は次のように表せる:

§18 集積点

実数あるいは実数に対応する直線上の点を集めたもの (定義は問わない) を、数や点の集まり (aggregate) あるいは 集合 (set) と呼ぶ。例えば正の整数の集合や全ての有理点の集合が考えられる。

ここでは議論の都合上、幾何学の言葉を使う¹⁸。点集合 \(S\) が与えられたとして、任意の点 \(\xi\) 取る。\(\xi\) は \(S\) に属するかもしれないし属さないかもしれない。このとき二つの可能性がある。つまり (i) \([\xi - \delta, \xi + \delta]\) に \(S\) に属する点が \(\xi\) 以外にない¹⁹ように正数 \(\delta\) を取れる、(ii) そのような \(\xi\) を取れない、の二つである。

(ii) が真だとする。このとき任意の区間 \([\xi - \delta, \xi + \delta]\) は、その幅がどれだけ小さくとも、\(S\) に含まれる \(\xi\) でない点 \(\xi_{1}\) を持つ。このような場合に \(\xi\) を \(S\) の 集積点 (points of acumulation) と呼ぶ。区間 \([\xi - \delta, \xi + \delta]\) は一つだけではなく無限に多くの \(S\) の点を含むことが容易に示せる: \(\xi_{1}\) を取った後に、\(\xi\) の周りに区間 \([\xi - \delta_{1}, \xi + \delta_{1}]\) を \(\xi_{1}\) に触れないように取れる。するとこの区間にも \(S\) の要素が含まれるので、これを \(\xi_{2}\) とする。以上の議論は \(\xi_{1}\) を \(\xi_{2}\) に取り換えればもう一度繰り返すことができ、同様にして無限に行える。こうすると点 \[ \xi_{1},\quad \xi_{2},\quad \xi_{3},\quad \ldots \] を好きなだけ取れる。これらの点は全て \(S\) に属し、\([\xi - \delta, \xi + \delta]\) の内部にある。

§19 ワイエルシュトラスの定理

点集合の一般理論は解析学のより高度な分野で非常に興味深く重要になるが、その多くは本書のような本に含めるには難しすぎる。しかしデデキントの定理から導かれる基礎的な定理が一つあり、これは後で必要になる:

証明を示す。直線 \(\Lambda\) を次のようにして二つのクラス \(L\) と \(R\) に分ける: 点 \(P\) が \(L\) に属するのは \(P\) よりも左に \(S\) の点が無限にあるときであり、そうでないとき \(P\) は \(R\) に含まれる。するとデデキントの定理の (i) と (iii) が満たされる。さらに \(\alpha\) は \(L\) に含まれ \(\beta\) は \(R\) に含まれるので、条件 (ii) も満たされる。

よって点 \(\xi\) であって \(\delta\) の大きさに関わらず \(\xi - \delta\) が \(L\) に属し \(\xi + \delta\) が \(R\) に属するものが存在する。このとき \([\xi - \delta, \xi + \delta]\) は \(S\) の無限に多くの点を含むので、\(\xi\) が \(S\) の集積点となる。

第一章に関するその他の例

1. \(ax + by + cz = 0\) が (1) 全ての \(x,\ y,\ z\) について、(2) \(\alpha x + \beta y + \gamma z=0\) を満たす全ての \(x,\ y,\ z\) について、(3) \(\alpha x + \beta y + \gamma z=0\) と \(Ax + By + Cz = 0\) の両方を満たす任意の \(x,\ y,\ z\) について満たされるための条件はそれぞれ何か？

2. 任意の正の有理数は次の形をした表現をただ一つ持つ: \[ a_{1} + \frac{a_{2}}{1·2} + \cdots + \frac{a_{k}}{1·2·3\cdots k} \] ここで \(a_{1},\ a_{2},\ \ldots,\ a_{k}\) は整数であり、次が成り立つ: \[ 0 \leq a_{1},\quad 0 \leq a_{2} \lt 2,\quad 0 \leq a_{3} \lt 3,\quad \ldots,\quad 0 \lt a_{k} \lt k \]

3. 任意の正の有理数は次に示す単純な連分数を使った表現をただ一つ持つ: \[ a_{1} + \cfrac{1}{a_{2} + \cfrac{1}{a_{3} + \cfrac{1}{\cdots + \cfrac{1}{a_{n}}}}} \] ここで \(a_{1},\ a_{2},\ \ldots\) は正の整数であり、\(0\) になれるのは \(a_{1}\) だけである。

   [こういった連分数の理論は代数の教科書に載っている。有理数および無理数の表現方法に関するさらに詳しい情報はホブソン著 Theory of Functions of a Real Variable, pp.45–49 を参照]

4. \(9x^{3} - 6x^{2} + 15x - 10 = 0\) の有理根を (もしあるなら) 求めよ。

5. 直線 \(AB\) が点 \(C\) で黄金比に分割される、つまり \(AB·AC = BC^{2}\) だとする (Euc.ii.11)。\(AC/AB\) が無理数だと示せ。

   [幾何学を使った直接的な証明がブロムウィッチ著 Infinite Series, §:143, p.363 にある]

6. \(A\) は無理数である。\(a,\ b,\ c,\ d\) を有理数としたとき、\(\dfrac{aA + b}{cA + d}\) が有理数になるのはどんなときか？

7. 初等的な不等式: \(a_{1},\ a_{2},\ \ldots\) が \(0\) または正の数を表し、\(p,\ q,\ \ldots\) が正の整数を表すとする。\(a_{1}^{p} - a_{2}^{p}\) と \(a_{1}^{q} - a_{2}^{q}\) の符号は同じなので、\((a_{1}^{p} - a_{2}^{p}) (a_{1}^{q} - a_{2}^{q}) \geq 0\) つまり \[ a_{1}^{p+q} + a_{2}^{p+q} \geq a_{1}^{p} a_{2}^{q} + a_{1}^{q} a_{2}^{p} \qquad \text{(1)} \] が成り立つ。この方程式は次のようにも表現できる: \[ \frac{a_{1}^{p+q} + a_{2}^{p+q}}{2} \geq \left(\frac{a_{1}^{p} + a_{2}^{p}}{2}\right) \left(\frac{a_{1}^{q} + a_{2}^{q}}{2}\right) \qquad \text{(2)} \] これを繰り返し使うと、次の不等式が得られる: \[ \frac{a_{1}^{p+q+r+\cdots} + a_{2}^{p+q+r+\cdots}}{2} \geq \left(\frac{a_{1}^{p} + a_{2}^{p}}{2}\right) \left(\frac{a_{1}^{q} + a_{2}^{q}}{2}\right) \left(\frac{a_{1}^{r} + a_{2}^{r}}{2}\right) \cdots \qquad \text{(3)} \] 特に次が成り立つ: \[ \frac{a_{1}^{p} + a_{2}^{p}}{2} \geq \left(\frac{a_{1} + a_{2}}{2}\right)^{p} \qquad \text{(4)} \] (1) で \(p = q = 1\) または (4) で \(p = 2\) とすると \(a_{1}^{2} + a_{2}^{2} \geq 2a_{1} a_{2}\) の形を変えた不等式を得る。この不等式は正の数の算術平均が幾何平均と等しいかそれ以上になることを示す。

8. \(n\) 個の数への一般化: \(n\) 個の数 \(a_{1},\ a_{2},\ \ldots,\ a_{n}\) に対する (1) の形をした \(\frac{1}{2} n(n - 1)\) 個の不等式を全て足すと、次の不等式を得る: \[ n \sum{a^{p+q}} \geq \sum a^{p} \sum a^{q} \qquad \text{(5)} \] これを書き直すと \[ \frac{\sum a^{p+q}}{n} \geq \frac{\sum a^{p}}{n} \cdot \frac{\sum a^{q}}{n} \qquad \text{(6)} \] を得る。ここから \(\text{(3)}\) の自然な拡張が得られる。特に次の不等式が成り立つ: \[ \frac{\sum a^{p}}{n} \geq \left(\frac{\sum a}{n}\right)^{p} \qquad \text{(7)} \]

9. 算術平均と幾何平均に関する一般的な形の定理: \(a_{1},\ a_{2},\ \ldots,\ a_{n}\) の算術平均が幾何平均と等しいかそれ以上であることは別の不等式を使っても示せる。\(a_{i}\) の最大要素と最小要素 (最大要素または最小要素が複数あるならその中から適当に選ぶ) を \(a_{r}\) と \(a_{s}\) として、\(G\) を \(a_{i}\) の幾何平均とする。示したい命題は \(G = 0\) のとき明らかなので、\(G \gt 0\) と仮定する。このとき次のようにして \(a_{r}\) と \(a_{s}\) の値を取り換える: \[ a_{r}' = G,\quad a_{s}' = a_{r}a_{s}/G \] こうしても幾何平均の値は変わらない。そして \[ a_{r}' + a_{s}' - a_{r} - a_{s} = (a_{r} - G)(a_{s} - G)/G \leq 0 \] が成り立つから、算術平均の値も増加しない。

   この議論を (最大でも \(n\) 回) 繰り返せば \(a_{1},\ a_{2},\ \ldots,\ a_{n}\) を \(G\) で取り換えられる。最終的な算術平均は \(G\) だから、最初の値は \(G\) と等しいかそれ以上と分かる。

10. シュワルツの不等式: \(a_{1},\ a_{2},\ \ldots,\ a_{n}\) と \(b_{1},\ b_{2},\ \ldots,\ b_{n}\) を正または負の実数とする。次の等式は簡単に確かめられる: \[ \left(\sum a_{r} b_{r}\right)^{2} = \sum a_{r}^{2} \sum a_{s}^{2} - \sum (a_{r} b_{s} - a_{s} b_{r})^{2} \] ここで \(r\) と \(s\) は \(1,\ 2,\ \ldots,\ n\) の値を取る。ここから次の不等式が分かる: \[ \left(\sum a_{r} b_{r}\right)^{2} \leq \sum a_{r}^{2} \sum b_{r}^{2} \] この不等式はシュワルツの不等式として知られる (が、最初に発見したのはコーシーである)。

11. \(a_{1},\ a_{2},\ \ldots,\ a_{n}\) が全て正のとき、\(s_{n} = a_{1} + a_{2} + \cdots + a_{n}\) とすれば次の不等式が成り立つ: \[ (1 + a_{1})(1 + a_{2}) \cdots (1 + a_{n}) \leq 1 + s_{n} + \frac{s_{n}^{2}}{2!} + \cdots + \frac{s_{n}^{n}}{n!} \]

    (Math. Trip. 1909.)

12. \(a_{1},\ a_{2},\ \ldots,\ a_{n}\) と \(b_{1},\ b_{2},\ \ldots,\ b_{n}\) がそれぞれ降順に並んだ正の実数なら、次の不等式が成り立つ: \[ (a_{1} + a_{2} + \cdots + a_{n}) (b_{1} + b_{2} + \cdots + b_{n}) \leq n(a_{1}b_{1} + a_{2}b_{2} + \cdots + a_{n}b_{n}) \]

13. \(a, b, c,\ \ldots k\) と \(A, B, C,\ \ldots K\) が実数で前者が全て正なら、 \[ \frac{aA + bB + \cdots + kK}{a + b + \cdots + k} \] は \(A,\ B,\ \ldots,\ K\) の最大値と最小値の間にある。

14. \(\sqrt{p},\ \sqrt{q}\) を相似でない不尽根数とする。\(a + b\sqrt{p} + c\sqrt{q} + d\sqrt{pq} = 0\) で \(a,\ b,\ c,\ d\) が全て有理数なら、\(a = 0,\ b = 0,\ c = 0,\ d = 0\) が成り立つ。

    [有理数 \(M,\ N\) を使って \(\sqrt{p}\) を \(M + N \sqrt{q}\) と表し、§14 の定理を使う]

15. \(a\sqrt{2} + b\sqrt{3} + c\sqrt{5} = 0\) で \(a,\ b,\ c\) が有理数なら \(a = 0,\ b = 0,\ c = 0\) だと示せ。

16. \(\sqrt{p}\) と \(\sqrt{q}\) の有理係数多項式 (整数 \(m,\ n\) と有理数 \(A\) を使った \(A(\sqrt{p})^{m}(\sqrt{q})^{n}\) という形の項の和) は次の形で表せる: \[ a + b\sqrt{p} + c\sqrt{q} + d\sqrt{pq} \] ここで \(a,\ b,\ c,\ d\) は有理数とする。

17. \(a,\ b,\ c,\ d,\ e,\ f\) を有理数とする。\(\dfrac{a + b\sqrt{p} + c\sqrt{q}}{d + e\sqrt{p} + f\sqrt{q}}\) を次の形で表せ: \[ A + B\sqrt{p} + C\sqrt{q} + D\sqrt{pq} \] \(A,\ B,\ C,\ D\) は有理数とする。

    [次が示せる: \[ \begin{aligned} \frac{a + b\sqrt{p} + c\sqrt{q}}{d + e\sqrt{p} + f\sqrt{q}} & = \frac{(a + b\sqrt{p} + c\sqrt{q})(d + e\sqrt{p} - f\sqrt{q})} {(d + e\sqrt{p})^{2} - f^{2}q} \\ & = \frac{\alpha + \beta\sqrt{p} + \gamma\sqrt{q} + \delta\sqrt{pq}} {\epsilon + \zeta\sqrt{p}} \end{aligned} \] ここで \(\alpha,\ \beta,\ \ldots\) は有理数であり、簡単に求められる。後は分母と分子に \(\epsilon - \zeta\sqrt{p}\) を乗じれば答えが得られる。この結果を使えば次の等式を示せる: \[ \frac{1}{1 + \sqrt{2} + \sqrt{3}} = \frac{1}{2} + \frac{1}{4}\sqrt{2} - \frac{1}{4}\sqrt{6}] \]

18. \(a,\ b,\ x,\ y\) が有理数で次の等式を満たすとする: \[ (ay - bx)^{2} + 4(a - x)(b - y) = 0 \] このとき「\(x = a\) かつ \(y = b\)」と「\(1 - ab\) と \(1 - xy\) が両方とも有理数の二乗」のどちらかが成り立つ。

    (Math. Trip. 1903.)

19. \(a,\ h,\ b,\ a',\ h',\ b'\) を有理数として、次の等式を満たす \(x\) と \(y\) を考える: \[ \begin{aligned} ax^{2} + 2hxy + by^{2} & = 1,\\ a'x^{2} + 2h'xy + b'y^{2} & = 1 \end{aligned} \] この式を満たす全ての \(x\) と \(y\) が有理数なら \[ \begin{gathered} (h - h')^{2} - (a - a')(b - b'), \quad (ab' - a'b)^{2} + 4(ah' - a'h)(bh' - b'h) \end{gathered} \] はどちらも有理数の二乗である。

    (Math. Trip. 1899.)

20. \(\sqrt{2}\) と \(\sqrt{3}\) が、有理数係数の \(\sqrt{2} + \sqrt{3}\) の三次関数なことを示せ。また \(\sqrt{2} - \sqrt{6} + 3\) が二つの \(\sqrt{2} + \sqrt{3}\) の線形関数の比であることを示せ。

    (Math. Trip. 1905.)

21. 式 \[ \sqrt{a + 2m\sqrt{a - m^{2}}} + \sqrt{a - 2m\sqrt{a - m^{2}}} \] は \(2m^{2} \gt a \gt m^{2}\) なら \(2m\) に等しく、\(a \gt 2m^{2}\) なら \(2\sqrt{a - m^{2}}\) に等しい。

22. \(\sqrt[3]{2}\) の任意の有理係数多項式は、有理数 \(a,\ b,\ c\) を使った次の形で表せる: \[ a + b\sqrt[3]{2} + c\sqrt[3]{4} \]

    さらに一般的に言うと、正の整数 \(p\) について \(\sqrt[m]{p}\) の有理係数多項式は次の形で表せる: \[ a_{0} + a_{1}\alpha + a_{2}\alpha^{2} + \cdots + a_{m-1}\alpha^{m-1} \] ここで \(a_{0},\ a_{1},\ \ldots\) は有理数で、\(\alpha = \sqrt[m]{p}\) とする。証明は次の通り。この形の任意の多項式は有理数 \(b_{0},\ b_{1},\ \ldots\ b_{k}\) を使って \[ b_{0} + b_{1}\alpha + b_{2}\alpha^{2} + \cdots + b_{k}\alpha^{k} \] と表せる。もし \(k \leq m - 1\) ならその時点で求めたい形が手に入っている。\(k \gt m - 1\) とすると、整数 \(\lambda\) と \(0 \leq s \leq m - 1\) を使って任意の \(r \gt m - 1\) を \(r = \lambda m + s\) と表せるので、\(\alpha^{r} = \alpha^{\lambda m + s} = p^{\lambda}\alpha^{s}\) が成り立つ。よって \(m - 1\) より大きい指数を持つ項を取り除ける。

23. \((\sqrt[3]{2} - 1)^{5}\) と \((\sqrt[3]{2} - 1)/(\sqrt[3]{2} + 1)\) を有理数 \(a,\ b,\ c\) を使って \(a + b\sqrt[3]{2} + c\sqrt[3]{4}\) の形で表せ。 [二番目の式では分母と分子に \(\sqrt[3]{4} - \sqrt[3]{2} + 1\) を乗じる]

24. もし \[ a + b\sqrt[3]{2} + c\sqrt[3]{4} = 0 \] で \(a,\ b,\ c\) が有理数なら、\(a = 0,\ b = 0,\ c = 0\) が成り立つ。

    [\(y = \sqrt[3]{2}\) とすると、\(y^{3} = 2\) かつ \[ cy^{2} + by + a = 0 \] が成り立つ。よって \(2cy^{2} + 2by + ay^{3} = 0\) すなわち \[ ay^{2} + 2cy + 2b = 0 \] である。二つの式に \(a\) と \(b\) を乗じて引くと \((ab - 2c^{2})y + a^{2} - 2bc = 0\) を得る。ここから \(y = -(a^{2} - 2bc)/(ab - 2c^{2})\) が有理数と分かるが、これはあり得ない。残された唯一の選択肢は \(ab - 2c^{2} = 0\) かつ \(a^{2} - 2bc = 0\) である。

    よって \(ab = 2c^{2}\) かつ \(a^{4} = 4b^{2}c^{2}\) と分かる。\(a\) も \(b\) もゼロでないなら、二つ目の式を一つ目の式で割って \(a^{3} = 2b^{3}\) を得る。しかし \(\sqrt[3]{2}\) は有理数 \(a/b\) にならないので、これはあり得ない。よって \(ab = 0\) かつ \(c = 0\) であり、最初の方程式から \(a,\ b,\ c\) が全て \(0\) だと分かる。

    系として、もし \(a + b\sqrt[3]{2} + c\sqrt[3]{4} = d + e\sqrt[3]{2} + f\sqrt[3]{4}\) なら \(a = d,\ b = e,\ c = f\) となる。

    より一般的に言えば、もし \[ a_{0} + a_{1}p^{1/m} + \cdots + a_{m-1}p^{(m-1)/m} = 0 \] であって \(p\) の \(m\) 乗が整数でないなら、\(a_{0} = a_{1} = \cdots = a_{m-1} = 0\) が成り立つ。証明は難しくない]

25. もし \(A + \sqrt[3]{B} = C + \sqrt[3]{D}\) なら、「\(A = C\) かつ \(B = D\)」または「\(B\) と \(D\) の両方が有理数の三乗」が成り立つ。

26. もし \(\sqrt[3]{A} + \sqrt[3]{B} + \sqrt[3]{C} = 0\) なら、「\(A,\ B,\ C\) の一つが \(0\) で残りの二つは符号が逆で大きさが同じ数」または「\(\sqrt[3]{A},\ \sqrt[3]{B},\ \sqrt[3]{C}\) の全てが同じ不尽根数 \(\sqrt[3]{X}\) の有理数倍」が成り立つ。

27. 次の等式を満たす有理数 \(\alpha,\ \beta\) を見つけよ: \[ \sqrt[3]{7 + 5\sqrt{2}} = \alpha + \beta\sqrt{2} \]

28. もし \((a - b^{3})b \gt 0\) なら \[ \sqrt[3]{a + \frac{9b^{3} + a}{3b}\sqrt{\frac{a - b^{3}}{3b}}} + \sqrt[3]{a - \frac{9b^{3} + a}{3b}\sqrt{\frac{a - b^{3}}{3b}}} \] は有理数である。 [三乗根の中の数はどちらも \[ \left(\alpha + \beta\sqrt{\frac{a - b^{3}}{3b}}\right)^{3} \] という形になる (\(\alpha\) と \(\beta\) は有理数)]

29. \(\alpha = \sqrt[n]{p}\) とすると、任意の \(\alpha\) の多項式は次数が \(n\) の有理係数方程式の根である。

    [\(\alpha\) の多項式を \(x\) とすれば、\(x\) は次の形に表せる: \[ x = l_{1} + m_{1}\alpha + \cdots + r_{1}\alpha^{(n-1)} \] ここで \(l_{1},\ m_{1},\ \ldots\) は有理数である (問題 22 の結果を使った)。

    同様に次の等式が成り立つとする: \[ x^{2} = l_{2} + m_{2}a + \cdots + r_{2}a^{(n-1)}, \] \[ \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \cdots \] \[ x^{n} = l_{n} + m_{n}a + \cdots + r_{n}a^{(n-1)} \]

    このとき \[ L_{1}x + L_{2}x^{2} + \cdots + L_{n}x^{n} = \Delta \] が成り立つ。ここで \(\Delta\) は行列式 \[ \left| \begin{array}{cccc} l_{1} & m_{1} & \cdots & r_{1} \\ l_{2} & m_{2} & \cdots & r_{2} \\ \vdots & \vdots & \ddots & \vdots \\ l_{n} & m_{n} & \cdots & r_{n} \\ \end{array} \right| \] であり、\(L_{1},\ L_{2},\ \ldots\) は \(l_{1},\ l_{2},\ \ldots\) に関する小行列式を表す]

30. 前問の操作を \(x = p + \sqrt{q}\) に適用し、§14 の定理を導け。

31. \(y = a + bp^{1/3} + cp^{2/3}\) が次の式を満たすことを示せ: \[ y^{3} - 3ay^{2} + 3y(a^{2} - bcp) - a^{3} - b^{3}p - c^{3}p^{2} + 3abcp = 0 \]

32. 代数的数: 次の形をした方程式の根となる無理数 (\(\sqrt{2}\) など) があることを見た: \[ a_{0}x^{n} + a_{1}x^{n-1} + \cdots + a_{n} = 0 \] ここで \(a_{0},\ a_{1},\ \ldots,\ a_{n}\) は整数である。このような無理数を代数的数 (algebraical number) と呼ぶ。そうでない全ての数 (例えば §15 で触れた \(\pi\)) を超越数 (trancendental number) と呼ぶ。\(x\) が代数的数なら、有理数 \(k\) に対する \(kx\) および整数 \(m,\ n\) に対する \(x^{m/n}\) も代数的数であることを示せ。

33. \(x\) と \(y\) が代数的数なら、\(x + y,\ x - y,\ xy,\ x/y\) も代数的数である。

    [仮定から次の等式が成り立つ: \[ a_{0}x^{m} + a_{1}x^{m-1} + \cdots + a_{m} = 0, \quad b_{0}y^{n} + b_{1}y^{n-1} + \cdots + b_{n} = 0 \] \(a_{i}\) と \(b_{i}\) は整数を表す。\(x + y = z\) すなわち \(y = z - x\) としてさらに \(x\) を消すと、似た形の等式 \[ c_{0}z^{p} + c_{1}z^{p-1} + \cdots + c_{p} = 0 \] が \(z\) によって満たされることが分かる。他の場合も同様]

34. もし \[ a_{0}x^{n} + a_{1}x^{n-1} + \cdots + a_{n} = 0 \] で \(a_{0},\ a_{1},\ \ldots,\ a_{n}\) が代数的数なら、\(x\) は代数的数である。 [仮定から \(n + 1\) 個の等式 \[ a_{0, r}a_{r}^{m_{r}} + a_{1, r}a_{r}^{m_{r}-1} + \cdots + a_{m_{r}, r} = 0\quad (r = 0,\ 1,\ \ldots,\ n) \] が手に入る。ここで係数 \(a_{0, r},\ a_{1, r},\ \ldots\) は整数を表す。これらの等式と最初の \(x\) に関する方程式から \(a_{0},\ a_{1},\ \ldots,\ a_{n}\) を打ち消す]

35. 前問の処理を \(x^{2} - 2x\sqrt{2} + \sqrt{3} = 0\) に適用せよ。

    [答えは \(x^{8} - 16x^{6} + 58x^{4} - 48x^{2} + 9 = 0\) である]

36. 次の数が満たす有理係数方程式を求めよ: \[ \begin{gathered} 1 + \sqrt{2} + \sqrt{3},\quad \frac{\sqrt{3} + \sqrt{2}} {\sqrt{3} - \sqrt{2}},\quad \sqrt{\sqrt{3}+ \sqrt{2}} + \sqrt{\sqrt{3} - \sqrt{2}},\quad \sqrt[3]{2} + \sqrt[3]{3} \end{gathered} \]

37. \(x^{3} = x + 1\) なら、次の \(a_{n},\ b_{n},\ c_{n}\) を使って \(x^{3n} = a_{n}x + b_{n} + c_{n}/x\) と表せる: \[ a_{n+1} = a_{n} + b_{n},\quad b_{n+1} = a_{n} + b_{n} + c_{n},\quad c_{n+1} = a_{n} + c_{n} \]

38. \(x^{6} + x^{5} - 2x^{4} - x^{3} + x^{2} + 1 = 0\) かつ \(y = x^{4} - x^{2} + x - 1\) なら、\(y\) は有理係数の二次方程式を満たす。

    (Math. Trip. 1903.)

    [ \(y^{2} + y + 1 = 0\) となるだろう]

1. この処理が常に行えるという仮定はアルキメデスの公理 (Axiom of Archimedes) と呼ばれる命題と同値である。^[return]

2. 訳注: 「クラス (class)」は何かの集まりを意味する。^[return]

3. この考え方はこの本の第一版から採用している。^[return]

4. これらの節はブロムウィッチ著 Infinite Series, Appendix I から取った。^[return]

5. 有理数がアルファベットを使って表されるなら、それに対応する切断はギリシャ文字を使って表すのが分かりやすいだろう。^[return]

6. 全ての有理数が下のクラスまたは上のクラスに属する切断もある。この二つの切断を正の無限大および負の無限大という実数としないのはなぜかと疑問に思うかもしれない。

   こうしても論理的な間違いはないが、実用上不便になる。例えば最も自然な加算と乗算の定義が上手く行かなくなる。さらに初学者にとって解析学で主な困難となるのは「無限 (infinity)」という言葉を含む言い回しに対する正確な感覚の習得だが、経験から言って、無限大という新しい数を追加すると彼らを混乱させてしまうことが多い。^[return]

7. つまり \((a)\) は \((b)\) に含まれ、かつ \((b)\) と同じではない。^[return]

8. つまり \(ax^{2} + 2bc + c = 0\) を満たす \(x\) の値が二つある。\(b^{2} - ac \lt 0\) ならその条件を満たす \(x\) は存在しない。初等代数ではそのような場合に「虚」根が存在すると言うことを読者は知っているはずである。この言葉の意味は 第三章 で説明される。

   \(b^{2} = ac\) のとき方程式は根を一つだけ持つ。考え方を統一するために「二つの等しい」根を持つと言う場合が多いが、これは慣習に過ぎない。^[return]

9. 図では \(b\) と \(c\) の符号が同じで、\(a\) の符号が異なっている。他の場合の図も書いてみるとよい。^[return]

10. この構築はクライン著 Leçons sur certaines questions de géométrie élémentaire (J・グリースによる仏訳, 1896, Paris) から取った。^[return]

11. この命題は仮定に過ぎない。これを採用できる理由は、(i) 幾何学の目的を考えれば十分である、そして (ii) 解析学における手続きの幾何学的な図示がしやすくなる、ためである。私たちは幾何学の言語を図示にのみ用いるので、幾何学の基礎を掘り下げる必要はない。^[return]

12. 訳注: この等式は \(z = \sqrt[3]{4 + \sqrt{15}} + \sqrt[3]{4 - \sqrt{15}}\) で満たされる。^[return]

13. この証明は第七章にある。^[return]

14. ホブソン著 Trigonometry (3rd edition), pp. 305 et seq. あるいは同じくホブソン著 Squaring the Circle (Cambridge, 1913) を参照。^[return]

15. これ以降の議論は §6 の議論と様々な部分で似ているが、ある程度の反復を避けようとはしていない。この「切断」という考え方はデデキントによる有名な論文 Stetigkeit und irrationale Zahlen で広まった。この本の読者であればこの考え方を理解できるだろうし、実のところ §6–§12 で触れた無理数の記法に関する議論を飛ばした読者であっても理解しておかなければならない。^[return]

16. §6 では可能性が三つあった。^[return]

17. §6 ではそうでなかった。^[return]

18. この講義の唯一の目的が言語の習得であることは忘れてよい。^[return]

19. \(\xi\) が \(S\) に含まれない場合には「\(\xi\)以外に」の部分を省く。^[return]