§108 陰関数定理

陰関数については前に第二章で説明した。例えば \(x\) と \(y\) が \[ y^{5} - xy - y - x = 0 \qquad \text{(1)} \] という関係で結ばれているなら、\(y\) は \(x\) の "陰関数" となる。

しかしこういった方程式が本当に \(x\) の関数 \(y\) を定義するかは証明なしには分からないし、複数の関数が定義される可能性もある。第二章では関数が定義されるのを当然として話を進めたが、ここまでの知識を使えばこれを正当化できる。

話を簡単にするために、用語を次のように定める。§107 と同様に、点 \((a, b)\) を囲む四角形であって特定の条件が成り立つものを考える。そのような四角形を \((a, b)\) の近傍 (neighborhood) と呼び、条件が \(\bm{(a, b)}\) の近傍で成り立つ、あるいは \(\bm{(a, b)}\) の近くで成り立つと言う。これは考えている条件が成り立つように四角形を一つ取れることだけを意味する。「直線上の区間」を「四角形」に置き換えれば、一変数の関数で使ったのと同じ言い回しが使える。

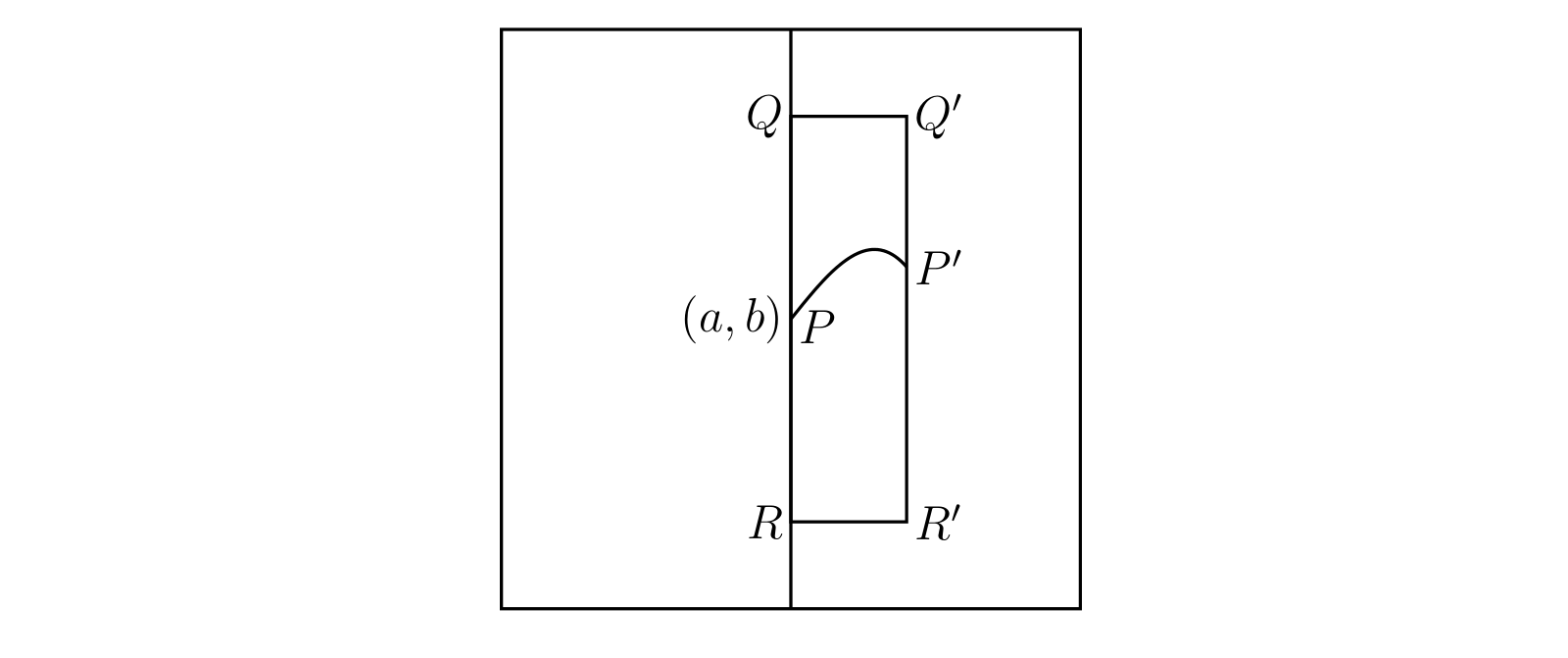
図 35 の四角形が条件 (i) と (iii) が成り立つ \((a, b)\) の近傍で、\(P\) が点 \((a, b)\) を表す。\(Q\) と \(R\) を図のように取ると、\(Q\) では \(f(x, y)\) が正で \(R\) では \(f(x, y)\) が負なことが (iii) から分かる。さらに \(f(x, y)\) が \(Q\) と \(R\) で連続なので、\(x\) 軸に平行な直線 \(QQ'\) と \(RR'\) を取ってその直線上で \(f(x, y)\) が常に正および負であるようにできる。特に \(Q'\) と \(R'\) で \(f(x, y)\) はそれぞれ正および負であり、(iii) と §100 から \(f(x, y)\) が \(0\) になる \(R'Q'\) 上の点 \(P'\) がただ一つ存在すると分かる。同様の議論を使えば \(RQ\) と \(R'Q'\) の間にある全ての垂直な直線上に \(f(x, y) = 0\) となる点を取れる。さらに \(RQ\) の左側にも点を取れるので、こういった点 \(P'\) を集めれば存在を示すべき関数 \(y = \phi(x)\) のグラフが得られる。

後は \(\phi(x)\) が連続だと示せばよい。\(x \to a\) における \(\phi(x)\) の上極限 \(\Lambda\) と下極限 \(\lambda\) (§96) を考えると議論が簡単になる。\((a, \lambda)\) は \(QR\) 上にあり、加えて \(x \to a\) で \(\phi(x) \to \lambda\) となるような \(x\) の値の列を見つけられる。\(f(x, \phi(x)) = 0\) で \(f(x, y)\) は \(x\) と \(y\) の連続関数なので \[ f(a, \lambda) = 0 \] が分かる。よって \(\lambda = b\) であり、同様に \(\Lambda = b\) も成り立つ。つまり \(x \to a\) のとき \(\phi(x)\) は極限 \(b\) に向かうので、\(\phi(x)\) は \(x = a\) で連続と分かる。\(x\) が \(a\) の近傍にあるときも同様に \(\phi(x)\) の連続性を示せる。

また定理の条件 (iii) の「狭義単調増加」を「狭義単調減少」に変えても結論は変わらないことも分かる。

例として、式 \(\text{(1)}\) で \(a = 0,\ b = 0\) とした場合を考える。条件 (i) と (ii) は明らかに成り立つ。加えて \[ f(x, y) - f(x, y') = (y - y') (y^{4} + y^{3}y' + y^{2}{y'}^{2} + y{y'}^{3} + {y'}^{4} - x - 1) \] は \(x,\ y,\ y'\) が小さいとき \(y - y'\) と逆の符号を持つので、条件 (iii) も (「増加」を「減少」として) 満たされる。ここから等式 \(\text{(1)}\) を恒等的に満たす連続関数 \(y\) であって \(x = 0\) で \(\phi(x) = 0\) を満たすものがあり、しかもそれは一つだけしか存在しないことが分かる。

次の等式を考えても同じ結論が得られる: \[ y^{2} - xy - y - x = 0 \] この場合、得られる関数は \[ y = \dfrac{1}{2}\{1 + x - \sqrt{1 + 6 x + x^{2}}\} \] となる。ただし根号は正の値を取るとする。もう一つの根号の値だと \(x = 0\) のとき関数の値が \(0\) にならない。

ここで気を付けるべき点がもう一つある。定理の条件に「\((a, b)\) の近傍」という言葉があるが、これはとある正方形 \(\xi - \delta \leq x \leq \xi + \delta,\ \eta - \delta \leq y \leq \eta + \delta\) を考えている。そして結論が成り立つのは \(x = a\) の近傍、つまり \(\xi - \delta_{1} \leq x \leq \xi + \delta_{1}\) という形の区間においてだけである。結論の \(\delta_{1}\) が条件の \(\delta\) と同じであるとは示されていないし、一般的に言って同じにならない。