§33 空間内の軌跡
三つの次元を持つ空間では、本質的に異なる二つの軌跡が存在する。最も単純な例はそれぞれ直線と平面である。
直線上を移動する点は一次の自由度しか持たない。点の移動方向は固定され、その位置は固定点からの距離という一つの情報で完全に決定される。例えば直線として第一章で考えた基準直線 \(\Lambda\) を取れば、直線上の任意の点の位置は一つの座標 \(x\) で決定される。一方で平面上を動く点には二次の自由度があり、その位置の決定には二つの座標が必要となる。
一つの方程式 \[ z = f(x, y) \] が表す軌跡は二つ目のクラスに属する軌跡であり、曲面 (surface) と呼ばれる。この曲面は「曲面」という言葉から常識的に想像される特徴を持っていることもあれば持っていないこともある (簡単で単純なケースであれば普通は持っている)。
§31 での考察を一般化すれば、\(f(x, y, z)\) という三つの変数を持つ関数 (あるいは任意の数の変数を持つ関数) を定義できる。そして §32 で \(f(x, y) = 0\) を平面曲線の方程式の標準形として採用したように、これからは \[ f(x, y, z) = 0 \] を曲面の方程式の標準形として採用する。
\(z = f(x, y)\) あるいは \(f(x, y, z) = 0\) という形の方程式が二つあるなら、それは軌跡は第一のクラスに属する軌跡を定義する。例えば直線は \(Ax + By + Cz + D = 0\) という形をした二つの方程式で表せる。また空間内の円は球と平面の交わりであり、次の二つの方程式で表せる: \[ \begin{gathered} (x - \alpha)^{2} + (y - \beta)^{2} + (z - \gamma)^{2} = \rho^{2},\\ Ax + By + Cz + D = 0 \end{gathered} \]
-
\(f(x, y, z) = 0\) の形をした方程式が三つある場合、何を表すか?
-
三つの線形方程式は一般に単一の点を表す。例外はどんな場合か?
-
平面 \(XOY\) を曲面とみなしたとき、この曲面上の平面曲線 \(f(x, y) = 0\) の方程式は何か? [\(f(x, y) = 0,\ z = 0\)]
-
柱体: \(f(x, y) = 0\) という単一の方程式を三次元空間内の軌跡とみなしたとき、これは何を意味するか?
[この曲面上の全ての点は \(f(x, y) = 0\) を満たし、そのときの \(z\) の値は考慮されない。曲線 \(f(x, y) = 0,\ z = 0\) はこの曲面を平面 \(XOY\) で切ったものであり、この曲線上の全ての点から \(OZ\) 方向に直線を引くと考えている曲面となる。この曲面を柱体 (cylinder) と呼ぶ]
-
曲面の平面上における表現、等高線: 曲面を平面に描画するなど不可能に思える: 実際不可能である。しかし次の方法を使えば曲面の主な性質を理解できることが多い。考えている曲面の方程式を \(z = f(x, y)\) とする。
\(z\) に具体的な値 \(a\) を与えると、方程式 \(f(x, y) = a\) が手に入る。これは紙面上のとある平面曲線を定義しているとみなせるので、この曲線を描いて \((a)\) とする。この曲線 \((a)\) は曲面の \(z = a\) の部分を平面 \(XOY\) に射影したものである。全ての \(a\) の値についてこれを行う (もちろん実際には適当に選んだ \(a\) に対して行う) と、図 17 のような図が得られる。英国陸地測量部による等高線地図が思い浮かぶだろう: 実際そういった地図は同じような方法で作られる。地図の \(1000\) という等高線は、海面上 \(1000\) ft にある海面と平行な平面で陸地を切ったものを海面上の平面に射影したものである1。
 図 17
図 17 -
曲面 \(2z = 3xy\) を表す等高線を描け。
-
正円錐: 座標系の原点を円錐の頂点とし、\(z\) 軸を円錐の軸と同じ方向とする。さらに \(\alpha\) を円錐の母線と軸のなす角度とすれば、円錐の方程式は \(x^{2} + y^{2} - z^{2} \tan^{2} \alpha = 0\) である (曲面は頂点から \(z\) 軸の両方向に存在する)。
-
一般的な回転曲面: 問題 7 の正円錐を平面 \(ZOX\) で切ると、方程式 \(x^{2} = z^{2}\tan^{2}\alpha\) で表される二つの直線が手に入る。つまり曲線 \(y = 0,\ x^{2} = z^{2}\tan^{2}\alpha\) を \(z\) 軸の周りに回転させて得られる曲面の方程式は、二番目の方程式の \(x^{2}\) を \(x^{2} + y^{2}\) に変えると得られる。一般的に言って、曲線 \(y = 0,\ x = f(z)\) を \(z\) 軸の周りに回転させて得られる曲面の方程式が次の形をしていることを示せ: \[ \sqrt{x^{2} + y^{2}} = f(z) \]
-
一般化された錐: ある固定された点を通る直線によって構成される曲面を錐 (cone) と呼び、その点を錐の頂点 (vertex) と呼ぶ。問題 7 で考えた正円錐は錐の例である。頂点が \(O\) である錐の方程式が \(f(z/x, z/y) = 0\) という形をしていること、およびこの形をした方程式が錐を表すことを示せ。
-
線識面: 柱と錐は多数の直線から構成される曲面の一種である。このような曲面を線識面 (ruled surface) と呼ぶ。
二つの方程式 \[ x = az + b,\quad y = cz + d \qquad \text{(1)} \] は二つの平面の交わり、すなわち直線を表す。ここで \(a,\ b,\ c,\ d\) が固定されておらず、補助変数 \(t\) の関数だとする。すると \(t\) の値それぞれについて、方程式 (1) が直線を定める。\(t\) が変化すると直線が移動し、曲面が生成される。この曲面の方程式は二つの方程式 (1) から \(t\) を削除すれば得られる。例えば問題 7 の正円錐を生成する二つの方程式は \[ x = z\tan \alpha\cos t,\quad y = z\tan \alpha\sin t \] となる。ここで \(t\) は考えている直線と \(z\) 軸を通る平面と平面 \(XOZ\) のなす角度を表す。
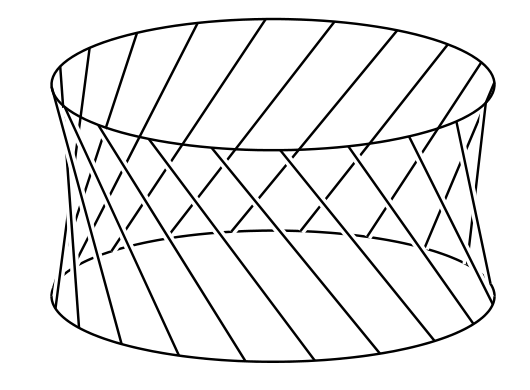
簡単な線識面の例をもう一つ示す。軸に平行な円柱の断面であって \(l\) だけ離れたものを二つ取る (図 18a)。このとき円柱の側面は \(PQ\) のような長さ \(l\) の平行な竿が集まったものとみなせる。このとき棒の両端は半径 \(a\) の円形の竿を二つ構成する。
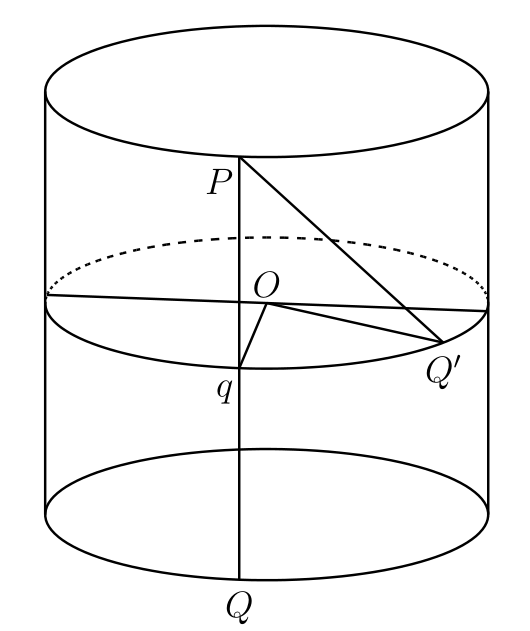 図 18a
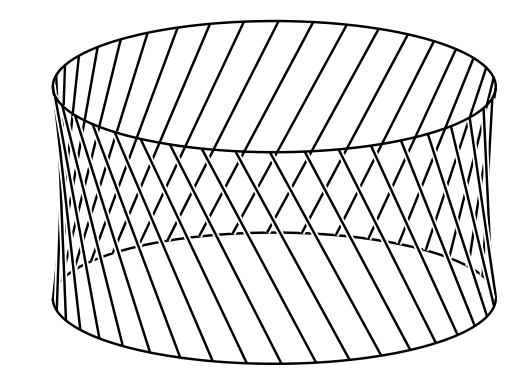
図 18aここで新たな竿として、同じ半径を持った円形の竿を上下どちらかの円から \(h\) だけ離れた位置に追加する (図 18a では \(Pq = h\) となっている)。\(Q\) を \(PQ\) から切り離し、\(Q\) が第三の円に \(Q'\) で触れるように傾ける。図中の \(\angle qQQ' = \alpha\) は次の式を満たす: \[ l^{2} - h^{2} = q{Q'}^{2} = \left (2a\sin\frac{1}{2} \alpha\right)^{2} \] 正円錐を構成する竿の全てに同じ操作を行うと、図 18b のような線識面が手に入る。この線識面は直線だけから構成されているにもかかわらず、いたるところが曲がっている。形としてはテーブルナプキンを丸めたものに近い (図 18c)。
-
地球の曲率は無視している。[return]