§193 べき級数の収束領域 (収束円)
\(z = r\) を正の実軸上の任意の点とする。べき級数が \(z = r\) で収束するなら、その級数は円 \(|z| = r\) 内部の全ての点で絶対収束する。特に \(r\) より小さい全ての実数の \(z\) で収束する。
正の軸軸上の点 \(r\) を次のようにして二つのクラスに分ける。一つのクラスには級数が収束する点を入れ、もう一つには収束しない点を入れる。一つ目のクラスは少なくとも一つの点 \(z = 0\) を含むが、級数が全ての \(z\) で収束することもあるので、二つ目のクラスは存在しない可能性がある。ただここでは二つ目のクラスが存在し、さらに一つ目のクラスには \(z = 0\) 以外の点が含まれると仮定する。すると一つ目のクラスに属する全ての点は二つ目のクラスに含まれる点の左側にある。よって二つのクラスを分ける点が存在し、その点は二つのクラスのどちらかに属する。この点を \(z = R\) とすれば、級数は円 \(\bm{|z| = R}\) 内部の全ての点で絶対収束する。
証明は次の通り。円 \(|z| = R\) と正の実軸の交点を \(A\) とする。円 \(|z| = R\) 内部の任意の点を \(P\) とすると、中心が \(O\) で半径が \(R\) より小さく \(P\) を含む円が描ける。この円と \(OA\) が交わる点を \(Q\) とすると級数は \(Q\) で収束し、結果 B から \(P\) で絶対収束すると分かる。
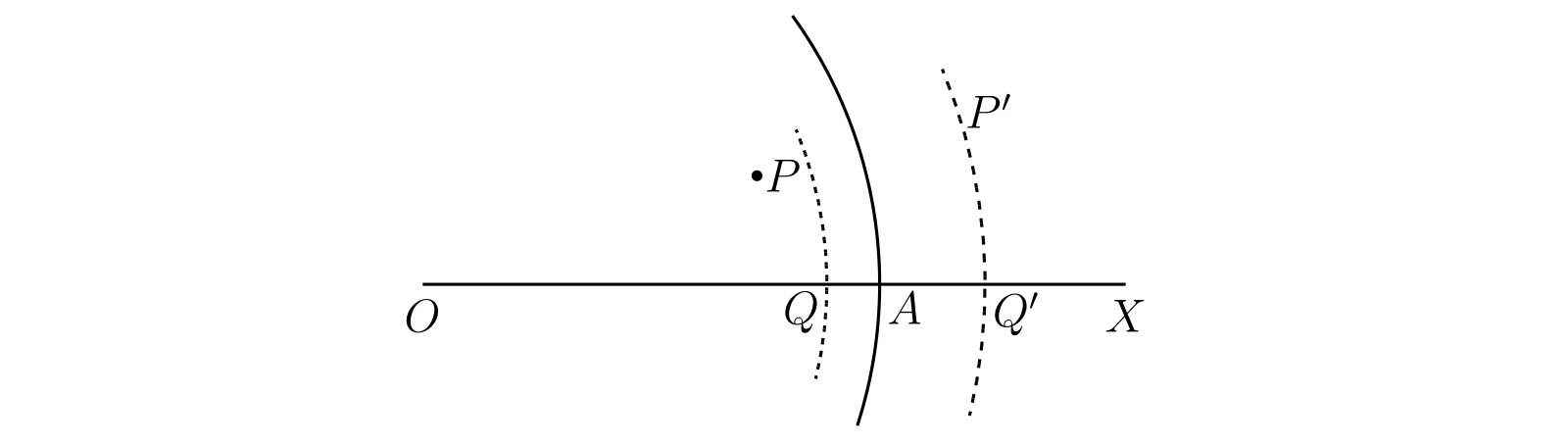
一方で円 \(|z| = R\) の外側にある任意の \(P'\) で級数は収束しない。もし \(P'\) で収束するなら \(P'\) よりも原点に近い全ての点で絶対収束するが、仮定より \(A\) と \(Q'\) の間の点では収束しないのでこれはあり得ない (図 51)。
今までに考えたべき級数の振る舞いには他に二つある: (1) 正の実軸上では \(z = 0\) を除いて任意の点で収束しない (2) 実軸上の全ての点で収束する。容易に分かるように (1) の場合には \(z = 0\) 以外で収束せず、(2) の場合には全ての場所で収束する。以上より次の結果が得られる:
任意のべき級数に対して、次のいずれかが成り立つ:
- \(z = 0\) でのみ収束する。
- 全ての \(z\) で絶対収束する。
- 原点が中心で半径 \(R\) の円の内側にある全ての \(z\) で絶対収束し、その外側にある全ての \(z\) で収束しない。
(3) の円を級数の収束円 (circle of convergence) と呼び、収束円の半径を収束半径 (radius of convergence) と呼ぶ。
ここで注意すべきなのが、この結果からは収束円上の点における級数の振る舞いについては何も分からない点である。次の例で様々な可能性があり得ることを示す。
-
\(a \gt 0\) に対する級数 \(1 + az + a^{2}z^{2} + \cdots\) は \(1/a\) の収束半径を持つ。収束円上では収束せず、\(z = 1/a\) では発散し、収束円上の他の点では有限に振動する。
-
級数 \(\dfrac{z}{1^{2}} + \dfrac{z^{2}}{2^{2}} + \dfrac{z^{3}}{3^{2}} + \cdots\) の収束半径は \(1\) であり、収束円上の全ての点で絶対収束する。
-
より一般に言うと、\(n \to \infty\) で \(|a_{n+1}|/|a_{n}| \to \lambda\) または \(|a_{n}|^{1/n} \to \lambda\) なら、級数 \(a_{0} + a_{1}z + a_{2}z^{2} + \cdots\) の収束半径は \(1/\lambda\) となる。一つ目の場合には \(|z|\) が \(1/\lambda\) より小さいなら \[ \lim \frac{|a_{n+1}z^{n+1}|}{|a_{n}z^{n}|} = \lambda |z| \] が \(1\) より小さくなり、そうでなければ \(1\) よりも大きくなる。後はダランベールの判定法 (§168 の結果 3) を使えば収束が示せる。二つ目の場合にはコーシーの判定法 (§168 の結果 2) を使って同様に議論できる。
-
対数級数: 級数 \[ z - \dfrac{1}{2} z^{2} + \dfrac{1}{3} z^{3} - \cdots \] は "対数" 級数 (logarithmic series) と呼ばれる (こう呼ばれる理由は後述する)。問題 3 を使うとこの級数の収束半径が \(1\) だと分かる。
\(z\) が収束円上にあるときを考える。\(z = \cos\theta + i\sin\theta\) とすれば、対数級数は \[ \cos\theta - \dfrac{1}{2} \cos 2\theta + \dfrac{1}{3} \cos 3\theta - \cdots + i(\sin\theta - \dfrac{1}{2} \sin 2\theta + \dfrac{1}{3} \sin 3\theta - \cdots) \] となる。
よって \(\theta\) が \(\pi\) の奇数倍でないとき実部と虚部は収束するが、絶対収束はしない (例 79.3)。\(\theta\) が \(\pi\) の奇数倍なら \(z = -1\) であり、このときの対数級数 \(-1 - \frac{1}{2} - \frac{1}{3} - \cdots\) は \(-\infty\) に発散する。よって対数級数は収束円上の \(z = -1\) 以外の全ての点で収束すると結論できる。
-
二項級数: 次の級数を考える: \[ 1 + mz + \frac{m(m - 1)}{2!} z^{2} + \frac{m(m - 1)(m - 2)}{3!} z^{3} + \cdots \] \(m\) が正の整数なら、この級数は有限項で打ち切られる。一般には \[ \frac{|a_{n+1}|}{|a_{n}|} = \frac{|m - n|}{n + 1} \to 1 \] なので、収束半径は \(1\) となる。収束円上における収束性は少し難しいのでここでは議論しない1。
-
Bromwich, Infinite Series, pp. 225 et seq. および Plane Trigonometry, (3rd edition), pp. 268 et seq. を参照。[return]