§21 関数の図示

変数 \(y\) が変数 \(x\) の関数だとする。この関数が表す \(x\) と \(y\) の関係を \(y\) の関数 \(x\) とみなすこともできるが、ここでは前者の視点に立って \(y\) を \(x\) の関数とみなして話を進める。このとき \(x\) を独立変数 (independent variable) と呼び、\(y\) を従属変数 (dependent variable) と呼ぶ。関数が表す関係が持つ形式が明らかでないときには、関数が存在するという事実を次の式で表す: \[ y = f(x) \] \(f(x)\) ではなく \(F(x),\ \phi(x),\ \psi(x),\ \ldots\) を使うこともある。

多くの場合で、関数の性質は次のように図示すると非常に分かりやすくなる。直行する二つの直線 \(OX,\ OY\) を両方向に無限に伸ばし、\(x\) と \(y\) の値をそれぞれ \(O\) から \(OX,\ OY\) に沿って測った長さで表す。もちろん符号を考慮し、図 6 のように正の方向に矢印を付ける。

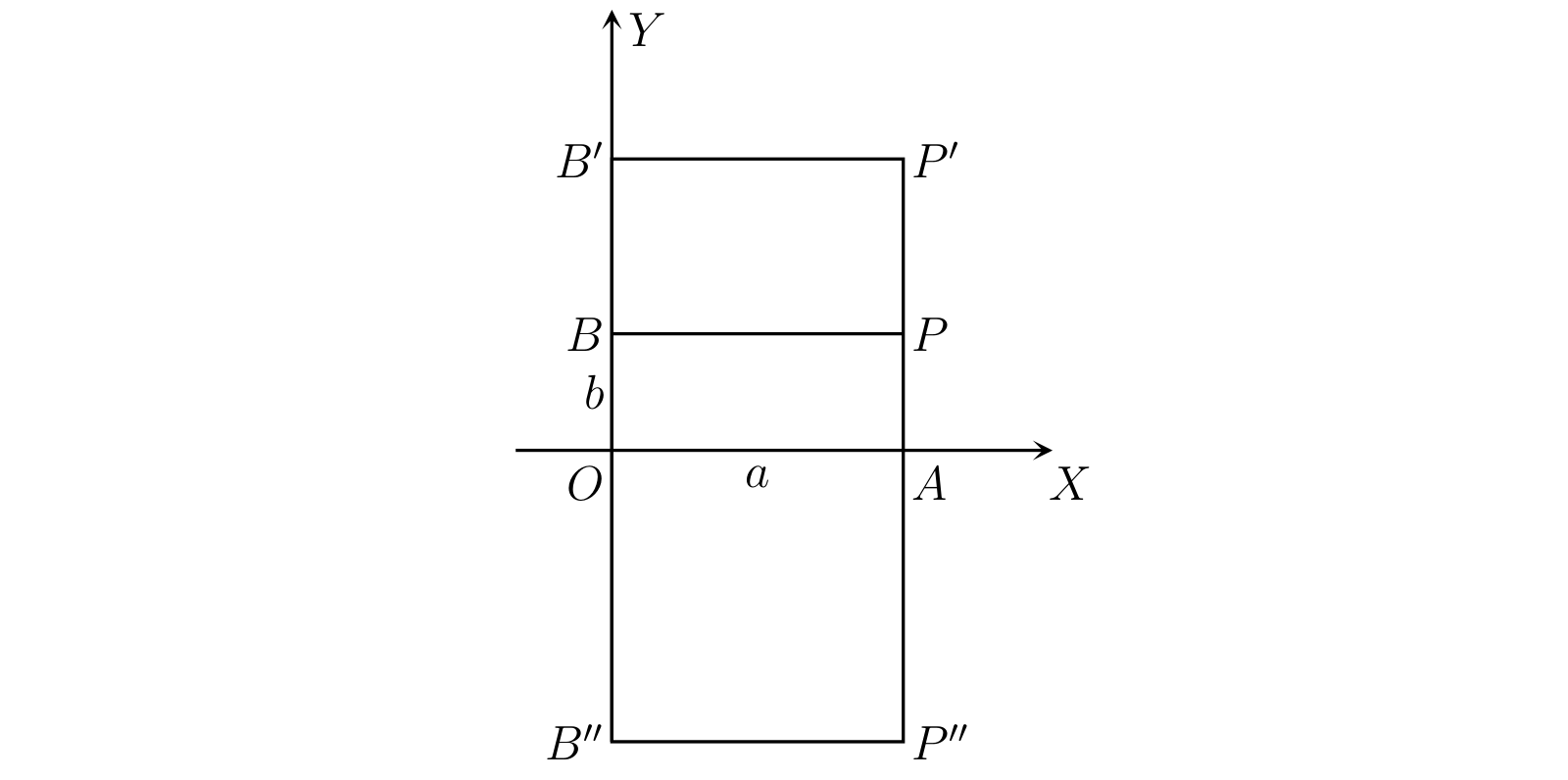
\(a\) を \(x\) の適当な値とし、\(a\) に対応する \(y\) の値 \(b\) が定義されているとする。\(OA = a\) と \(OB = b\) を取り、長方形 \(OAPB\) を描き、図中で \(P\) と印の付いた点を考える。このように印を付けた点 \(P\) は \(x = a\) に対する \(y\) の値が \(b\) であることを示しているとみなせる。

\(x\) の値 \(a\) が複数の \(y\) の値 (例えば \(b,\ b',\ b''\)) に対応するなら、一つの点 \(P\) の代わりに複数の点 \(P,\ P',\ P''\) が取れる。

\(P\) を点 (point) \((a, b)\) と呼び、\(a\) と \(b\) を軸 \(OX,\ OY\) に沿った \(P\) の座標 (coordinate) と呼ぶ。\(a\) は \(P\) の横座標 (abscissa) であり、\(b\) は \(P\) の縦座標 (ordinate) である。\(OX\) と \(OY\) はそれぞれ \(x\) 軸 (axis of \(x\)) および \(y\) 軸 (axis of \(y\)) と呼び、両方まとめて座標軸 (axis of coordinate) と呼ぶ。\(O\) は座標原点 (origin of coordinate) あるいは原点 (origin) と呼ばれる。

\(y\) の値 \(b\) (あるいは \(b,\ b',\ b'',\ \ldots\)) が定義される全ての \(x\) の値 \(a\) に対応する点 \(P\) (あるいは \(P,\ P',\ P'',\ \ldots\)) が定まったとする。それらの点全ての集まりを関数 \(y\) のグラフ と呼ぶ。

非常に簡単な例として、\(y\) が次の方程式で定義される \(x\) の関数である場合を考える: \[ Ax + By + C = 0 \qquad \text{(1)} \] ここで \(A,\ B,\ C\) は固定された実数とする¹。このとき \(y\) は \(x\) の関数であり、§20 で示した三つの特徴を全て持つ。そして \(\bm{y}\) のグラフが直線であることは容易に示せる。この命題の証明は解析幾何学の教科書に載っているし、読者もいくつか知っているだろう。

異なる表現を使うこともある。つまり「\(x\) と \(y\) が方程式 (1) を満たしならが動くとき、点 \(\bm{(x, y)}\) の軌跡が直線になる」と言うことがある。このとき方程式 (1) を軌跡の方程式と呼び、この方程式が軌跡を表すと表現する。この「軌跡」や「軌跡の方程式」という言葉は非常によく使われ、\(x\) と \(y\) の関係が解析的な式で表せるときにはいつでも考えられる。

\(Ax + By + C\) は一次より大きい項が含まれない最も一般的な \(x\) と \(y\) の多項式なので、方程式 \(Ax + By + C = 0\) は一般的な一次方程式である。つまり一般的な一次方程式は直線を表す。これと逆の命題「直線の方程式は一次方程式である」も簡単に示せる。

興味深い幾何学的な軌跡をさらにいくつか示す。方程式 \[ (x - \alpha)^{2} + (y - \beta)^{2} = \rho^{2} \] および \[ x^{2} + y^{2} + 2Gx + 2Fy + C = 0, \] はどちらも円を表す。ただし二番目の方程式では \(G^{2} + F^{2} - C \gt 0\) とする。また \[ Ax^{2} + 2Hxy + By^{2} + 2Gx + 2Fy + C = 0 \] (一般的な二次方程式) は、係数が特定の不等式を満たすという条件の下で、円錐曲線 (楕円・放物線・双曲線) を表す。こういった軌跡に関するさらなる議論は解析幾何学の本に譲る。

1. \(B = 0\) だと方程式から \(y\) が消える。このとき \(y\) は \(x = -C/A\) という単一の値に対してのみ定義される関数とみなされる。この \(x\) に対して \(y\) は全ての値を取る。^[return]