§46 複素変数の有理関数
複素数の有理関数に関する定理をさらにいくつか紹介する。複素変数 \(z\) の有理関数 (rational function) の定義は実変数 \(x\) の有理関数の定義と全く同じであり、二つの \(z\) の多項式の商と定義される。
任意の有理関数 \(R(z)\) は \(x\) と \(y\) の実数係数有理関数 \(X\) と \(Y\) を使って \(X + Yi\) と書ける。
まず加算と乗算の定義から、任意の多項式 \(P(x + yi)\) が \(x\) と \(y\) の実数係数多項式 \(A\) と \(B\) を使って \(A + Bi\) と書けることが分かる。同様に \(Q(x + yi)\) も \(C + Di\) と書ける。よって \[ R(x + yi) = \frac{P(x + yi)}{Q(x + yi)} \] は次のように変形できる: \[ \begin{aligned} \frac{A + Bi}{C + Di} & = \frac{(A + Bi) (C - Di)}{(C + Di) (C - Di)}\\ & = \frac{AC + BD}{C^{2} + D^{2}} + \frac{BC - AD}{C^{2} + D^{2}} i \end{aligned} \] 上述の定理はここから従う。
\(R(z)\) が実数係数の有理関数で、\(R(x + yi) = X + Yi\) が一つ前の定理で示した形のとき、\(R(x - yi) = X - Yi\) が成り立つ。
まず \((x + yi)^{n}\) に対するこの定理は実際に展開すれば容易に得られる。それを足せば実数係数の多項式に対しても成り立つことが分かる。よって一つ前の定理と同じ表記を使えば \[ R(x - yi) = \frac{A - Bi}{C - Di} = \frac{AC + BD}{C^{2} + D^{2}} - \frac{BC - AD}{C^{2} + D^{2}}i \] となる。これは \(i\) の符号が反転している点以外は \(R(x + yi)\) と等しい。この二つの定理は複素変数の数がいくつでも成り立つ。
実数係数の方程式 \[ a_{0}z^{n} + a_{1}z^{n-1} + \cdots + a_{n} = 0 \] の実数でない根は、共役な複素数の組からなる。
\(x + yi\) が根のときは \(x - yi\) も根であることが二番目の定理から分かる。この定理の特殊な場合として、実数係数二次方程式の根が実数または共役な複素数であるという §43 で示した結果が得られる。
この定理は次のように表現されることもある: 実数係数の多項式では、複素根は共役な組として表れる。これを 例 8.7 で示した有理数係数の多項式では、無理根が共役な組として現れるという事実と比較するとよい1。
-
§45 の定理 (6) を定義から直接、幾何学的な手段を使わずに示せ。
[まず \(|z + z'| \leq |z| + |z'|\) を示すために \[ (x + x')^{2} + (y + y')^{2} \leq \left\{\sqrt{x^{2} + y^{2}} + \sqrt{{x'}^{2} + {y'}^{2}}\right\}^{2} \] を示す。一般の場合へは簡単に拡張できる]
-
等式 \[ |z| + |z'| + \cdots = |z + z' + \cdots| \] が成り立つのは \(z,\ z',\ \ldots\ \) が全て同じ偏角を持つ場合に限ることを示せ。幾何学的な証明と解析的な証明の両方を示すこと。
-
任意個の複素数の和の大きさは、その実部 (または虚部) の和より大きくない。
-
二つの複素数の和と積がどちらも実数とする。このとき両方とも実数であるか、そうでなければ共役である。
-
もし \[ a + b\sqrt{2} + (c + d \sqrt{2})i = A + B\sqrt{2} + (C + D\sqrt{2})i \] で \(a,\ b,\ c,\ d,\ A,\ B,\ C,\ D\) が全て有理数の実数なら、以下が成り立つ: \[ a = A,\quad b = B,\quad c = C,\quad d = D \]
-
次の数を実数 \(A,\ B\) を使った \(A + Bi\) という形で表せ: \[ (1 + i)^{2},\quad \left(\frac{1 + i}{1 - i}\right)^{2},\quad \left(\frac{1 - i}{1 + i}\right)^{2},\quad \frac{\lambda + \mu i}{\lambda - \mu i},\quad \left(\frac{\lambda + \mu i}{\lambda - \mu i}\right)^{2} - \left(\frac{\lambda - \mu i}{\lambda + \mu i}\right)^{2} \] \(\lambda\) と \(\mu\) は実数とする。
-
次の \(z = x + yi\) の関数を、\(x\) と \(y\) の実関数 \(X\) と \(Y\) を使って \(X + Yi\) という形で表せ。\(\alpha,\ \beta,\ \gamma,\ \delta\) は実数とする: \[ z^{2},\quad z^{3},\quad z^{n},\quad \frac{1}{z},\quad z + \frac{1}{z},\quad \frac{\alpha + \beta z}{\gamma + \delta z} \]
-
上の二つの例に登場する複素数と関数の大きさを求めよ。
-
\(z = a\) と \(z = b\) および \(z = c\) と \(z = d\) をつないだ二つの直線が直行するのは \[ \arg\left(\frac{a - b}{c - d}\right) = ±\frac{1}{2} \pi \] が成り立つとき、つまり \((a - b)/(c - d)\) が純虚数なときだと示せ。二つの直線が平行になるための条件は何か?
-
三角形の三頂点が複素数 \(\alpha,\ \beta,\ \gamma\) を使って \(z = \alpha,\ z = \beta,\ z = \gamma\) と与えられる。次の命題を示せ:
- 重心は \(z = \frac{1}{3}(\alpha + \beta + \gamma)\) を満たす。
- 外心は \(|z - \alpha| = |z - \beta| = |z - \gamma|\) を満たす。
- 各頂点から反対側の辺に引いた垂線が交わる点は次の式を満たす: \[ \operatorname{Im}\left(\frac{z - \alpha}{\beta - \gamma}\right) = \operatorname{Im}\left(\frac{z - \beta}{\gamma - \alpha}\right) = \operatorname{Im}\left(\frac{z - \gamma}{\alpha - \beta}\right) = 0 \]
- 三角形の内部にある点 \(P\) であって \[ \angle CBP = \angle ACP = \angle BAP = \omega \] および次の式を満たすものが存在する: \[ \cot\omega = \cot A + \cot B + \cot C \]
[(iii) の証明では、\(z\) が表す点を \(P\) としたときに \(AP\) と \(BC\) が垂直となるための条件が「\((z - \alpha)/(\beta - \gamma)\) が純虚数」つまり次の式であることを利用する: \[ \operatorname{Re}(z - \alpha) \operatorname{Re}(\beta - \gamma) + \operatorname{Im}(z - \alpha) \operatorname{Im}(\beta - \gamma) = 0 \] この方程式の \(\alpha,\ \beta,\ \gamma\) を巡回させた三つの方程式は、全て同じ \(z\) によって満たされる。これは三つの左辺の和が \(0\) なことから分かる。
(iv) の証明は次のようにする。\(BC\) を \(x\) 軸正方向と平行に取ると2、次が成り立つ: \[ \gamma - \beta = a,\quad \alpha - \gamma = - b \operatorname{Cis}(-C),\quad \beta - \alpha = - c \operatorname{Cis} B \]
\(z\) と \(\omega\) は次の方程式から求めなければならない: \[ \frac{(z - \alpha)(\beta_{0} - \alpha_{0})} {(z_{0} - \alpha_{0})(\beta - \alpha)} = \frac{(z - \beta)(\gamma_{0} - \beta_{0})} {(z_{0} - \beta_{0})(\gamma - \beta)} = \frac{(z - \gamma)(\alpha_{0} - \gamma_{0})} {(z_{0} - \gamma_{0})(\alpha - \gamma)} = \operatorname{Cis} 2\omega \] ここで \(z_{0},\ \alpha_{0},\ \beta_{0},\ \gamma_{0}\) は \(z,\ \alpha,\ \beta,\ \gamma\) の共役を表す。
三つの式の分母と分子を足して、さらに \[ i\cot\omega = \frac{1 + \operatorname{Cis} 2\omega}{1 - \operatorname{Cis} 2\omega} \] を使えば \[ i\cot\omega = \frac{(\beta - \gamma)(\beta_{0} - \gamma_{0}) + (\gamma - \alpha)(\gamma_{0} - \alpha_{0}) + (\alpha - \beta)(\alpha_{0} - \beta_{0})} {\beta\gamma_{0} - \beta_{0}\gamma + \gamma\alpha_{0} - \gamma_{0}\alpha + \alpha\beta_{0} - \alpha_{0}\beta} \] が分かる。よって \(\Delta\) を三角形の面積とすれば、\(\cot\omega\) の値が \((a^{2} + b^{2} +c^{2})/4\Delta\) だと容易に示せる。これは示したい式と同値である。
\(z\) を求めるには、分数の等式の分母と分子にそれぞれ \((\gamma_{0} - \beta_{0})/(\beta - \alpha),\ (\alpha_{0} - \gamma_{0})/(\gamma - \beta),\ (\beta_{0} - \alpha_{0})/(\alpha - \gamma)\) を乗じる。すると最終的に \[ z = \frac{a\alpha \operatorname{Cis} A + b\beta \operatorname{Cis} B + c\gamma \operatorname{Cis} C} {a\operatorname{Cis} A + b\operatorname{Cis} B + c\operatorname{Cis} C} \] が求まる]
-
複素数 \(a,\ b,\ c\) と \(x,\ y,\ z\) からなる二つの三角形は、次の等式が成り立つとき相似となる: \[ \begin{vmatrix} 1 & 1 & 1\\ a & b & c \\ x & y & z \end{vmatrix} = 0 \]
[必要な条件は \(\overline{AB}/\overline{AC} = \overline{XY}/\overline{XZ}\) (小文字を引数に持つ点を大文字で表す) あるいは \((b - a)/(c - a) = (y - x)/(z - x)\) である]
-
\(x,\ y,\ z\) が一直線上にあるときには \(\alpha + \beta + \gamma = 0\) かつ \(\alpha x + \beta y + \gamma z = 0\) となるように実数 \(\alpha,\ \beta,\ \gamma\) を取れることを前問を使って示せ。またこの逆も示せ (参考: 例 20.4)。 [この設定では \(x,\ y,\ z\) からなる三角形が軸 \(OX\) 上にある潰れた三角形と相似になるので、前問の結果が適用できる]
-
複素係数の一般的な線形方程式: 方程式 \(\alpha z + \beta = 0\) は \(\alpha \neq 0\) なら唯一の解 \(z = -(\beta/\alpha)\) を持つ。もし \[ \alpha = a + Ai,\quad \beta = b + Bi,\quad z = x + yi \] なら、実部と虚数を等号で結ぶことで二つの実数 \(x\) と \(y\) を決定する二つの方程式を得る。\(y = 0\) なら方程式は実根を持ち、\(ax + b = 0,\ Ax + B = 0\) が成り立つ。この連立方程式が矛盾しない解を持つ条件は \(aB - bA = 0\) である。
-
複素係数の一般的な二次方程式は次の形をしている: \[ (a + Ai)z^{2} + 2(b + Bi)z + (c + Ci) = 0 \]
\(a\) と \(A\) が両方ともゼロでないなら \(a + iA\) で両辺を割れるので、 \[ z^{2} + 2(b + Bi)z + (c + Ci) = 0 \qquad \text{(1)} \] が一般的な形となる。\(z = x + yi\) を代入して実部と虚部をそれぞれ等号で結べば、\(x\) と \(y\) に関する連立方程式を得る: \[ x^{2} - y^{2} + 2(bx - By) + c = 0, \quad 2xy + 2(by + Bx) + C = 0 \]
さらに \[ x + b = \xi, \quad y + B = \eta, \quad b^{2} - B^{2} - c = h, \quad 2bB - C = k \] と置けば、次の式が得られる: \[ \xi^{2} - \eta^{2} = h, \quad 2\xi\eta = k \]
二乗して足せば \[ \begin{gathered} \xi^{2} + \eta^{2} = \sqrt{h^{2} + k^{2}}, \\ \xi = ±\sqrt{\tfrac{1}{2}\{\sqrt{h^{2} + k^{2}} + h\}}, \quad \eta = ±\sqrt{\tfrac{1}{2}\{\sqrt{h^{2} + k^{2}} - h\}} \end{gathered} \] を得る。ここで \(\xi\) と \(\eta\) の符号は \(\xi\eta\) の符号が \(k\) と同じになるよう選ぶ。つまり \(k\) が正なら同じ符号を、\(k\) が負なら違う符号を取る。
-
重根の条件: 二つの根が等しいのは「\(h = 0\) かつ \(k = 0\)」すなわち「\(c = b^{2} - B^{2}\) かつ \(C = 2bB\)」が成り立つときに限る。この条件は単一の式 \(c + Ci = (b + Bi)^{2}\) と同値であり、方程式 (1) の左辺が完全平方になることを意味する。
-
実根の条件: \(x^{2} + 2(b + Bi) x + (c + Ci) = 0\) を満たす \(x\) が実数なら、\(x^{2} + 2bx + c = 0\) かつ \(2Bx + C = 0\) となる。\(x\) を削除すればこの条件を単純化できる: \[ C^{2} - 4bBC + 4cB^{2} = 0 \]
-
純虚数根の条件: これは容易に分かる: \[ C^{2} - 4bBC - 4b^{2}c = 0 \]
-
共役な複素根の組の条件: 二つの共役な複素数の和と積はどちらも実数なので、\(b + Bi\) と \(c + Ci\) は両方とも実数である。つまり \(B = 0\) かつ \(C = 0\) でなければならない。よって (1) が共役な複素根を持つのは係数が実数のときに限る。根の明示的な表現を見てもこのことを確認できる。加えてもし \(b^2 \geq c\) ならこの場合でも根は実数となるので、共役な複素根のための条件は「\(B = 0\) かつ \(C = 0\) かつ \(b^{2} \lt c\)」となる。
-
-
三次方程式: \(G,\ H\) を複素数として \[ z^{3} + 3Hz + G = 0 \] を考える。この方程式にあり得るのは (i) 実根 (ii) 純虚根 (iii) 共役な複素根である。\(H = \lambda + \mu i\) および \(G = \rho + \sigma i\) とすれば、次が分かる:
-
実根の条件: \(\mu\) が \(0\) でないなら実根は \(-\sigma/3\mu\) であり、加えて \(\sigma^{3} + 27\lambda\mu^{2}\sigma - 27\mu^{3}\rho = 0\) が成り立つ。一方 \(\mu = 0\) なら \(\sigma = 0\) でもないと方程式の係数が実数とならない。後者の場合には三つの実根が存在する。
-
純虚根の条件: \(\mu\) が \(0\) でないなら純虚根は \((\rho/3\mu)i\) であり、\(\rho^{3} - 27\lambda\mu^{2}\rho - 27\mu^{3}\sigma = 0\) が成り立つ。一方 \(\mu = 0\) なら \(\rho = 0\) であり、純虚根は実数係数を持つ三次方程式 \(y^{3} - 3\lambda y - \sigma = 0\) の解 \(y\) を使って \(yi\) と表せる。後者の場合には三つの純虚根が存在する。
-
共役な複素根の組の条件: 根を \(x + yi,\ x - yi\) とすると、三つの根の和が \(0\) であることから三つ目の根は \(-2x\) となる。多項式の係数と根の関係から \[ y^{2} - 3x^{2} = 3H,\quad 2x(x^{2} + y^{2}) = G \] が分かる。よって \(G\) と \(H\) はどちらも実数でなくてはならない。
いずれの場合でも、実数係数の三次方程式への帰着もしくは根そのものが見つかる (見つかった根で方程式を割れば二次方程式に帰着できる)。
-
- \(a_{1} = A_{1} + A_{1}'i,\ \ldots\) として三次方程式 \(x^{3} + a_{1}x^{2} + a_{2}x + a_{3} = 0\) を考える。この方程式が共役な複素根の組を持つとき、\(A_{3}' \neq 0\) なら最後の根が \(-A_{1}'a_{3}/A_{3}'\) だと示せ。\(A_{3}' = 0\) のケースも調べよ。
-
\(z^{3} + 3Hz + G = 0\) が二つの虚数根を持つなら、方程式 \[ 8\alpha^{3} + 6\alpha H - G = 0 \] は一つの実根を持ち、それは一つ目の方程式の複素根の実部 \(\alpha\) であることを証明せよ。さらに \(\alpha\) の符号が \(G\) と同じことを示せ。
-
複素係数の方程式は、その次数に関わらず一般には実根や共役な複素根を持つとは限らない。方程式が (a) 実根あるいは (b) 共役な複素根の組を持つために係数が満たすべき条件はそれぞれ何か?
-
同軸円: 図 26 で \(A,\ B,\ P\) の引数を \(a,\ b,\ z\) とする。このとき主値を考えれば、 \[ \arg\frac{z - b}{z - a} = \angle APB \] が成り立つ。図中二つの円が等しいとする。\(P',\ P_{1},\ P_{1}'\) の引数が \(z',\ z_{1},\ z_{1}'\) で \(\angle APB = \theta\) なら \[ \arg\frac{z' - b}{z' - a} = \pi - \theta,\quad \arg\frac{z_{1} - b}{z_{1} - a} = -\theta \] および次が成り立つ: \[ \arg\frac{z_{1}' - b}{z_{1}' - a} = -\pi + \theta \]
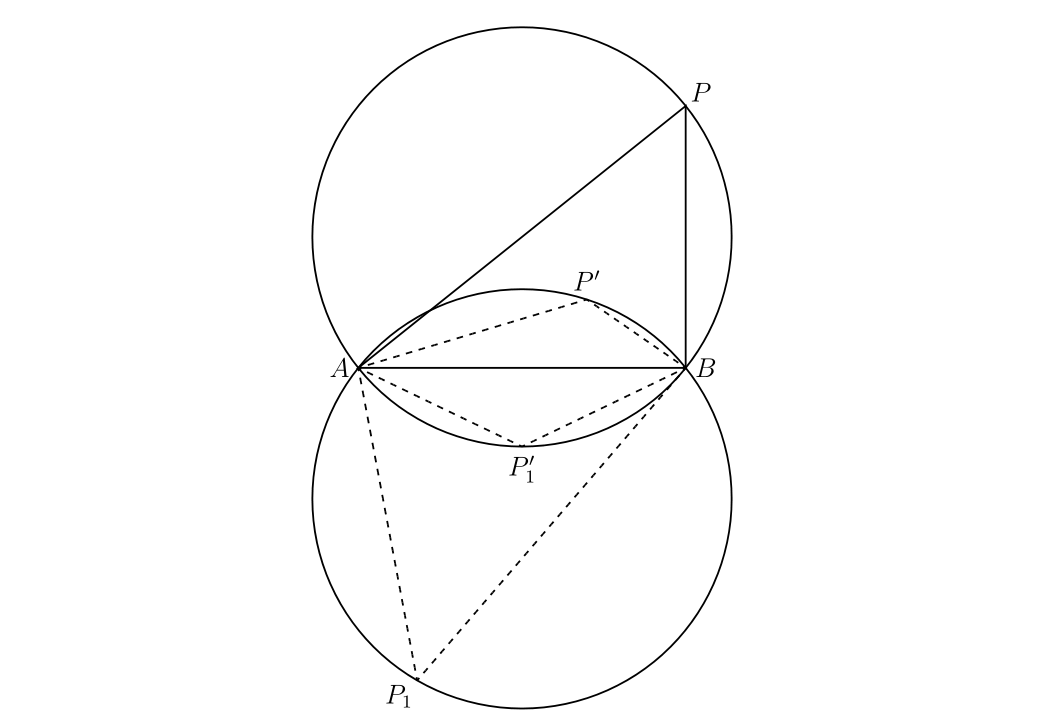 図 26
図 26\(\theta\) を定数とすると、方程式 \[ \arg\frac{z - b}{z - a} = \theta \] で定まる軌跡は弧 \(APB\) である。\(\theta\) の代わりに \(\pi - \theta,\ -\theta,\ -\pi + \theta\) とすれば、他の三つの弧も得られる。
\(\theta\) がパラメータだとする。このとき \(\theta\) を \(-\pi\) から \(\pi\) まで変化させて得られる方程式の系は二点 \(\bm{A,\ B}\) を通る円全体を表す。ここで一つの円は異なる \(\theta\) に対応する二つの部分から構成される。
-
方程式 \[ \left|\frac{z - b}{z - a}\right| = \lambda \qquad \text{(1)} \] を考える。\(\lambda\) は定数とする。
\(P\) を適当な点とし、三点 \(A\, B\, P\) を通る円の \(P\) を通る接線が \(AB\) と交わる点を \(K\) とする。このとき \(\triangle KPA\) と \(\triangle KBP\) は相似だから、次の式が成り立つ: \[ AP/PB = PK/BK = KA/KP = \lambda \] よって \(KA/KB = \lambda^{2}\) であり、方程式 (1) を満たす任意の \(P\) について \(K\) は固定点だと分かる。また \(KP^{2} = KA · KB\) であり、これは定数となる。よって \(\bm{P}\) の軌跡は \(\bm{K}\) を中心とする円である。
\(\lambda\) を変化させたときに得られる方程式の系は円の系を定義し、その円の全てが問題 19 で考えた系に含まれる全ての円と直行する。
問題 19 の系は共通点を持つ同軸円の系 (system of coaxal circles of the common point kind) と呼ばれる。問題 20 の系は 極限点を持つ同軸円の系 (system of coaxal circles of the limiting point kind) と呼ばれ、\(A\) と \(B\) を極原点 (limiting point) と呼ぶ。\(\lambda\) が非常に小さいあるいは非常に大きい場合、極限点 \(A,\ B\) を持つ同軸円は \(A\) または \(B\) を内部に含む非常に小さい円となる。
-
双一次変換: 次の方程式を考える: \[ z = Z + a \qquad \text{(1)} \] ここで \(z = x + yi\) と \(Z = X + Yi\) は複素変数であり、それぞれ平面 \(xoy\) と平面 \(XOY\) という異なる平面上にあるとする。全ての \(z\) の値には一つの \(Z\) の値が対応し、逆も成り立つ。\(a = \alpha + \beta i\) とすれば \[ x = X + \alpha,\quad y = Y + \beta \] であり、\((x, y)\) に \((X, Y)\) が対応する。もし \((x, y)\) が \(xoy\) 平面上のある曲線を表しているなら、\((X, Y)\) は \(XOY\) 平面における何らかの曲線を表す。つまり一方の平面上の任意の図形がもう一方の平面上の何らかの図形に対応する。(1) のような関係を使って平面 \(xoy\) 上の図形を平面 \(XOY\) 上の図形に対応付けるこの変形処理を、変換 (transformation) と呼ぶ。この例では二つの図形の間の関係が非常に簡単に定義されている。具体的に言うと \((X, Y)\) が表す図形は \((x, y)\) が表す図形と同じ大きさ・形・傾きを持ち、\(\alpha\) だけ左に、\(\beta\) だけ下に移動している。このような変換を移動 (translation) と呼ぶ。
次に方程式 \[ z = \rho Z \qquad \text{(2)} \] を考える (\(\rho\) は実数)。このとき \(x = \rho X,\ y = \rho Y\) が成り立つ。二つの図形は相似で、任意の点はそれぞれの原点から見て相似な点に配置される。\((x, y)\) の図形の大きさは \((X, Y)\) の図形の大きさの \(\rho\) 倍となる。こういった変換を拡大 (magnification) と呼ぶ。
最後に方程式 \[ z = (\cos\phi + i \sin\phi)Z \qquad \text{(3)} \] を考える。明らかに \(|z| = |Z|\) であり、\(\arg z\) と \(\arg Z + \phi\) はどこかで等しい。\((x, y)\) の図形と \((X, Y)\) の図形の唯一の違いは図形が原点中心に正方向に \(\phi\) だけ回転している点である。こういった変換を回転 (rotation) と呼ぶ。
一般的な線形変換 \[ z = aZ + b \qquad \text{(4)} \] は変換 (1), (2), (3) を組み合わせたものである。実際 \(|a| = \rho\) および \(\text{am a} = \phi\) とすれば、(4) を次の三つの式で表せる: \[ z = z' + b, \quad z' = \rho Z', \quad Z' = (\cos\phi + i\sin\phi)Z \] つまり一般的な線形変換は、移動・拡大・回転を組み合わせたものと等しい。
続いて次の変換を考える: \[ z = \frac{1}{Z} \qquad \text{(5)} \] \(|Z| = R\) および \(\arg Z = \Theta\) とすれば、\(|z| = 1/R\) と \(\arg z = -\Theta\) が成り立つ。\((x, y)\) の図形から \((X, Y)\) の図形を得るには、まず前者を原点中心に単位円に関して反転させ、次に軸 \(ox\) に関して図を反転させればよい。
最後に変換 \[ z = \frac{aZ + b}{cZ + d} \qquad \text{(6)} \] を考える。これは次の変換を組み合わせたものと等しい: \[ \begin{aligned} z & = (a/c) + (bc - ad)(z'/c), \\ z' & = 1/Z', \\ Z' & = cZ + d \end{aligned} \] 言い換えると、これまでに考えた全ての種類の変換をとある順番で組み合わせたものは式 (6) で表せる。
変換 (6) を一般双一次変換 (general bilinear transformation) と呼ぶ。\(Z\) について解けば次を得る: \[ Z = \frac{dz - b}{cz - a} \]
全ての \(z\) の値がちょうど一つの \(Z\) の値に対応し、さらにその逆も成り立つような変換を考えた場合、一般双一次変換はその中で最も一般的な変換である。
-
一般双一次変換は円を円に変換する: 証明は何種類かある。反転が円を円に (特殊ケースでは直線に) 変換するというよく知られた幾何学の定理を使うこともできるし、問題 19 と問題 20 の結果を使うこともできる。例えば点 \((x, y)\) から構成される円が \[ \left| \frac{z - \sigma}{z - \rho} \right| = \lambda \] なら、\(z\) に \(Z\) を代入すれば \[ \left|\frac{Z - \sigma'}{Z - \rho'} \right| = \lambda' \] を得る。新しい記号は次の通り: \[ \sigma' = -\frac{b - \sigma d}{a - \sigma c}, \quad \rho' = -\frac{b - \rho d}{a - \rho c}, \quad \lambda' = \left|\frac{a - \rho c}{a - \sigma c}\right|\lambda \]
-
変換 \(z = 1/Z,\ z = (1 + Z)/(1 - Z)\) について、(1) 原点中心の円および (2) 原点を通る直線のそれぞれに対応する曲線 \((X, Y)\) を描け。
-
変換 \(z = (aZ + b)/(cZ + d)\) が円 \(x^{2} + y^{2} = 1\) を直線に変換するための条件は \(|a| = |c|\) である。
-
複比 (cross ratio) \((z_{1}, z_{2}; z_{3}, z_{4})\) は次のように定義される: \[ \frac{(z_{1} - z_{3}) (z_{2} - z_{4})}{(z_{1} - z_{4}) (z_{2} - z_{3})} \]
四点 \(z_{1},\ z_{2},\ z_{3},\ z_{4}\) が同じ直線にあるなら、この定義は初等幾何学のものと同様になる。\(z_{1},\ z_{2},\ z_{3},\ z_{4}\) の添え字を入れ替えると \(24\) 個の複比を作れるが、その中には異なる値が \(6\) 個含まれる。複比の一つを \(\lambda\) とすれば、六つの複比は \(\lambda,\ 1 - \lambda,\ 1/\lambda,\ 1/(1 - \lambda,\ ) (\lambda - 1)/\lambda,\ \lambda/(\lambda - 1)\) である。これらの値のどれかが \(-1\) に等しいとき、四点は調和 (harmonic) である、あるいは調和関係にある (harmonically related) と言う。このとき六つの複比は \(-1,\ 2,\ -1,\ \frac{1}{2},\ 2,\ \frac{1}{2}\) となる。
複比のいずれかが実数なら全て実数であり、そのとき四点は同一円周上にある。なぜならこのとき \[ \arg\frac{(z_{1} - z_{3}) (z_{2} - z_{4})}{(z_{1} - z_{4}) (z_{2} - z_{3})} \] が \(-\pi,\ 0,\ \pi\) のいずれかであり、\(\arg\{(z_{1} - z_{3})/(z_{1} - z_{4})\}\) と \(\arg\{(z_{2} - z_{3})/(z_{2} - z_{4})\}\) は等しいか \(\pi\) だけ離れた値になるためである (参考: 問題 19)。
もし \({(z_{1}, z_{2}; z_{3}, z_{4})} = - 1\) なら、二つの条件 \[ \arg\frac{z_{1} - z_{3}}{z_{1} - z_{4}} = ±\pi + \arg\frac{z_{2} - z_{3}}{z_{2} - z_{4}},\quad \left|\frac{z_{1} - z_{3}}{z_{1} - z_{4}}\right| = \left|\frac{z_{2} - z_{3}}{z_{2} - z_{4}}\right| \] が満たされる。つまり四点 \(A_{1},\ A_{2},\ A_{3},\ A_{4}\) は同一円周上に存在し、\(A_{1}\) と \(A_{2}\) の間に \(A_{3}\) と \(A_{4}\) がある。さらに \(A_{1}A_{3}/A_{1}A_{4} = A_{2}A_{3}/A_{2}A_{4}\) が成り立つ: \(A_{3}A_{4}\) の中点を \(O\) とする。仮定の式 \[ \frac{(z_{1} - z_{3}) (z_{2} - z_{4})}{(z_{1} - z_{4}) (z_{2} - z_{3})} = -1 \] を変形すると \[ (z_{1} + z_{2}) (z_{3} + z_{4}) = 2(z_{1}z_{2} + z_{3}z_{4}) \] となり、さらに \[ \{z_{1} - \frac{1}{2}(z_{3} + z_{4})\} \{z_{2} - \frac{1}{2}(z_{3} + z_{4})\} = \{\frac{1}{2}(z_{3} - z_{4})\}^{2} \] とも書ける。これは \(\overline{OA_{1}} · \overline{OA_{2}} = \overline{OA_{3}}^{2} = \overline{OA_{4}}^{2}\) と同値である。よって \(OA_{1}\) が \(A_{3}A_{4}\) となす角度は \(OA_{2}\) が \(A_{3}A_{4}\) となす角度と等しく、さらに \(OA_{1} · OA_{2} = OA_{3}^{2} = OA_{4}^{2}\) と分かる。この議論における \(A_{1}, A_{2}\) と \(A_{3}, A_{4}\) の対称性に注目すれば、\(A_{1}A_{2}\) の中点 \(O'\) について \(O'A_{3}\) と \(A_{1}A_{2}\) がなす角度と \(O'A_{4}\) と \(A_{1}A_{2}\) がなす角度も等しく、さらに \(O'A_{3} · O'A_{4} = O'A_{1}^{2} = O'A_{2}^{2}\) も成り立つことが分かる。
-
点 \(A_{1},\ A_{2}\) が \(az^{2} + 2bz + c = 0\) で与えられ、点 \(A_{3},\ A_{4}\) が \(a'z^{2} + 2b'z + c' = 0\) で与えられ、\(A_{3}A_{4}\) の中点が \(O\) であり、\(ac' + a'c - 2bb' = 0\) とする。このとき \(OA_{1}\) と \(OA_{2}\) が \(A_{3}A_{4}\) となす角度は等しく、\(OA_{1} · OA_{2} = OA_{3}^{2} = OA_{4}^{2}\) が成り立つ。
(Math. Trip. 1901.)
-
アルガン図において \(AB,\ CD\) を交点を持つ二つの線分とし、\(P,\ Q\) をそれらの中点とする。もし \(AB\) が \(\angle CPD\) を二等分して \(PA^{2} = PB^{2} = PC · PD\) なら、\(CD\) は \(\angle AQB\) を二等分して \(QC^{2} = QD^{2} = QA · QB\) なことを示せ
(Math. Trip. 1909.)
-
四点が円周上にある条件: 十分条件は複比のどれか (結局は全て) が実数なこと (問題 25) だが、この条件は必要でもある。別の表現を使うと、この条件は「次の式が成り立つように実数 \(\alpha,\ \beta,\ \gamma\) を選べること」となる: \[ \begin{vmatrix} 1 & 1 & 1\\ \alpha & \beta & \gamma\\ z_{1}z_{4} + z_{2}z_{3} & z_{2}z_{4} + z_{3}z_{1} & z_{3}z_{4} + z_{1}z_{2} \end{vmatrix} = 0 \] [証明には、変換 \(Z = 1/(z - z_{4})\) が点 \(z_{4}\) に関する反転処理に等しいことを使う (問題 21)。\(z_{1},\ z_{2},\ z_{3}\) が \(z_{4}\) を通る円周上にあるなら、変換先の点 \(Z_{1} = 1/(z_{1} - z_{4}),\ Z_{2} = 1/(z_{2} - z_{4}),\ Z_{3} = 1/(z_{3} - z_{4})\) は一直線上にある。よって (問題 12 から) 実数 \(\alpha',\ \beta',\ \gamma'\) であって \(\alpha' + \beta' + \gamma' = 0\) かつ \(\alpha'/(z_{1} - z_{4}) + \beta'/(z_{2} - z_{4}) + \gamma'/(z_{3} - z_{4}) = 0\) を満たすものが取れる。これが示したい式と同値なことは簡単に示せる]
-
ド・モアブルの定理と似た実数に対する次の命題を示せ: \(\phi_{1},\ \phi_{2},\ \phi_{3},\ \ldots\ \) が正の鋭角であり \[ \tan\phi_{m+1} = \tan\phi_{m} \sec\phi_{1} + \sec\phi_{m} \tan\phi_{1} \] を満たすなら、次の三つの式が成り立つ: \[ \tan\phi_{m+n} = \tan\phi_{m} \sec\phi_{n} + \sec\phi_{m} \tan\phi_{n}, \] \[ \sec\phi_{m+n} = \sec\phi_{m} \sec\phi_{n} + \tan\phi_{m} \tan\phi_{n} \] \[ \tan\phi_{m} + \sec\phi_{m} = (\tan\phi_{1} + \sec\phi_{1})^{m} \] [数学的帰納法を使う]
-
変換 \(\bm{z = Z^{m}}\): この変換では \(r = R^{m}\) であり、\(\theta\) は \(m\Theta\) から \(2\pi\) の整数倍だけ離れている。\(Z\) が単位円を一周する運動を表すなら、\(z\) は単位円を \(m\) 回周る運動を表す。
このとき \((X, Y)\) 平面を原点を中心に \(2\pi/m\) の角度で \(m\) 個に分割したものそれぞれに \((x, y)\) 平面全体が対応する。逆に \((x, y)\) 平面の各点には \((X, Y)\) 平面の \(m\) 点が対応する。
-
実数の複素関数: \(f(t)\) と \(\phi(t)\) を実変数 \(t\) のとある区間に対して定義された二つの実関数とする。このとき \[ z = f(t) + i\phi(t) \qquad \text{(1)} \] を \(t\) の複素関数 (complex function) と呼ぶ。この関数は次のようにすると曲線として幾何学的に表せる: \[ x = f(t),\quad y = \phi(t) \] この方程式から \(t\) を削除すれば曲線の方程式が得られる。\(z\) が \(t\) の多項式あるいは有理関数で係数が複素数なら、(1) の形に変形することで関数の表す曲線を求められる。
-
\(a\) と \(b\) が複素数で \[ z = a + (b - a)t \] とする。\(a = \alpha + \alpha' i,\ b = \beta + \beta' i\) なら \[ x = \alpha + (\beta - \alpha)t, \quad y = \alpha' + (\beta' - \alpha')t \] となる。関数が表す曲線は \(z = a\) と \(z = b\) を結ぶ直線である。二つの点の間の線分は \(0\) から \(1\) の \(t\) の値の区間に対応する。他の二つの半直線に対応する \(t\) の値を求めよ。
-
もし \[ z = c + \rho\left(\frac{1 + ti}{1 - ti}\right) \] で \(\rho\) が正なら、この関数が表すのは \(c\) を中心とした半径 \(\rho\) の円である。\(t\) が実数全体を動くと、\(z\) は円を一度だけ回る。
-
\(z = (a + bt)/(c + dt)\) という一般的な方程式は円を表す。\(x\) と \(y\) を代入して \(t\) を削除すれば示せるが、これは面倒である。問題 22 の結果を使えばより簡単に示せる: \(z = (a + bZ)/(c + dZ),\ Z = t\) とすれば、実数 \(t\) が動くと \(Z\) は \(X\) 軸上を動く。これは直線だから、\(z\) は円となる。
-
方程式 \[ z = a + 2bt + ct^{2} \] は一般に放物線を表す。\(b/c\) が実数なら直線となる。
-
\(\alpha,\ \beta,\ \gamma\) が実数なら、\(z = (a + 2bt + ct^{2})/(\alpha + 2\beta t + \gamma t^{2})\) は円錐曲線を表す。
[次の式から \(t\) を削除すればよい: \[ \begin{aligned} x & = (A + 2Bt + Ct^{2})/(\alpha + 2\beta t + \gamma t^{2}), \\ y & = (A' + 2B't + C't^{2})/(\alpha + 2\beta t + \gamma t^{2}) \end{aligned} \] ただし \(A + A'i = a,\ B + B'i = b,\ C + C'i = c\) である]
-