§178 被積分関数が正の無限積分
§177 の式 \(\text{(1)}\) で定義される無限積分の収束と発散に関して、§167 の定理 A–D と同様の関係を考える。定理 A が級数だけでなく積分でも正しいことは §177 の \(\text{(ii)}\) で見た。また定理 B に対応する命題は「無限積分 \(\text{(1)}\) が収束するための必要十分条件は、\(a\) より大きい全ての \(x\) で \[ \int_{a}^{x} \phi(t)\, dt \lt K \] となるよう \(K\) を取れること」となる。
同様に定理 C には「\(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) が収束し、\(a\) より大きい任意の \(x\) で \(\psi(x) \leq K\phi(x)\) なら、\(\displaystyle\int_{a}^{\infty} \psi(x)\, dx\) も収束して \[ \int_{a}^{\infty} \psi(x)\, dx \leq K\int_{a}^{\infty} \phi(x)\, dx \] が成り立つ」という命題が対応する。発散に対応する判定法の定式化は読者に任せる。
一方で §168 のダランベールの判定法に対応する積分に関する命題は存在しない。これは積分には "連続する項" が存在しないことによる。またコーシーの判定法に対応する命題は存在するが、あまり重要でない上に命題の定式化には関数 \(\phi(x) = r^{x}\) に関する詳細な議論 (第九章で行うもの) が必要になる。最も重要な判定法は次の積分との比較によって得られる: \[ \int_{a}^{\infty} \frac{dx}{x^{s}}\quad (a \gt 0) \] §175 で調べたこの積分の収束と発散についての結果を次にまとめる:
\(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) は \(s \gt 1\) に対して \(x \geq a\) で \(\phi(x) \lt Kx^{-s}\) なら収束し、\(s \leq 1\) に対して \(x \geq a\) で \(\phi(x) \gt Kx^{-s}\) なら発散する。特に \(\lim x^{s}\phi(x) = l\) で \(l \gt 0\) なら、積分は \(s \gt 1\) か \(s \leq 1\) かに応じて収束または発散する。
収束する無限級数の重要な性質の中に、対応する性質が無限積分にないものが一つある: \(\sum \phi(n)\) が収束するなら \(\phi(n) \to 0\) だが、\(\phi(x)\) が常に正で \(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) だとしても \(\phi(x) \to 0\) だとは限らない。
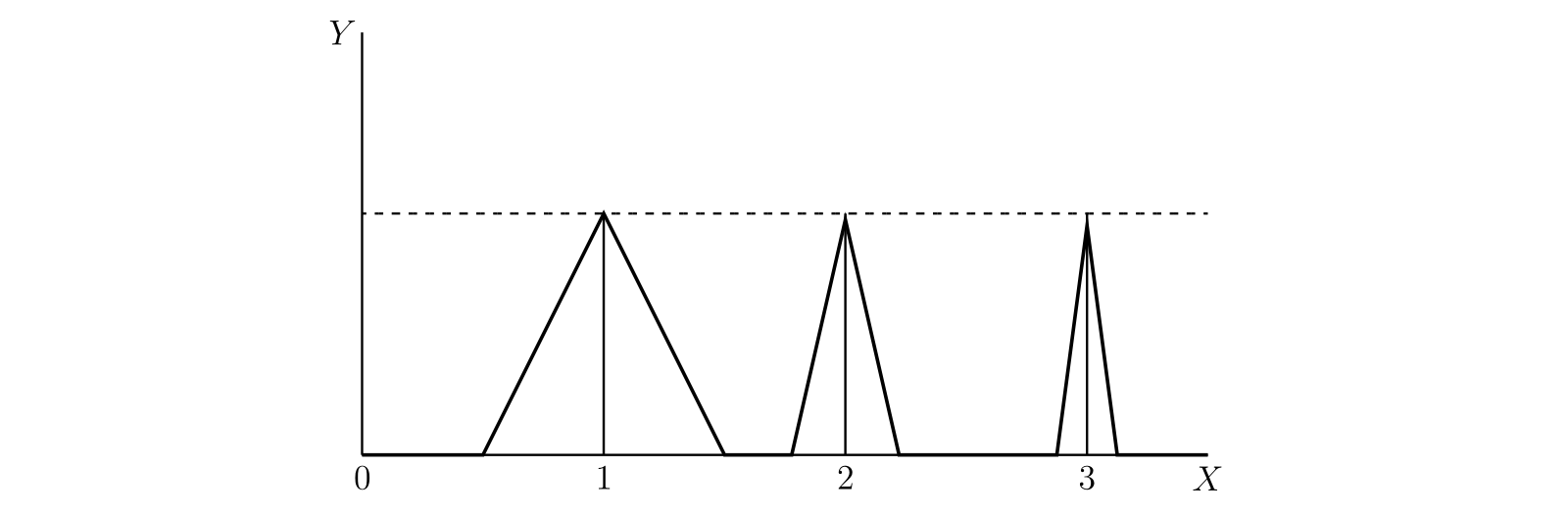
例としてグラフが次の図の細い線で表される関数 \(\phi(x)\) を考える。\(x = 1,\ 2,\ 3\) に対応するピークの高さは \(1\) で、幅は \(x = n\) のとき \(2/(n + 1)^{2}\) とする。ピークの面積は \(1/(n + 1)^{2}\) であり、任意の \(\xi\) に対して \[ \int_{0}^{\xi} \phi(x)\, dx \lt \sum_{0}^{\infty} \frac{1}{(n + 1)^{2}} \] が成り立つ。したがって \(\displaystyle\int_{0}^{\infty} \phi(x)\, dx\) は収束する。しかし \(\phi(x) \to 0\) は成り立たない。
-
積分 \[ \int_{a}^{\infty} \frac{\alpha x^{r} + \beta x^{r-1} + \cdots + \lambda} {Ax^{s} + Bx^{s-1} + \cdots + L}\, dx \] は \(s \gt r + 1\) なら収束し、それ以外のとき発散する。ただし \(\alpha\) と \(A\) は正で、\(a\) は分母の根の最大値より大きいとする。
-
次の積分のうち収束するのはどれか? \[ \displaystyle\int_{a}^{\infty} \frac{dx}{\sqrt{x}},\quad \displaystyle\int_{a}^{\infty} \frac{dx}{x^{4/3}}, \] \[ \int_{a}^{\infty} \frac{dx}{c^{2} + x^{2}},\quad \int_{a}^{\infty} \frac{x\, dx}{c^{2} + x^{2}},\quad \int_{a}^{\infty} \frac{x^{2}\, dx}{c^{2} + x^{2}},\quad \int_{a}^{\infty} \frac{x^{2}\, dx}{\alpha + 2\beta x^{2} + \gamma x^{4}} \] 最初の二つの積分では \(a \gt 0\) で、最後の積分では \(a\) が分母の根の最大値より大きいとする。
-
積分 \[ \int_{a}^{\xi} \cos x\, dx,\quad \int_{a}^{\xi} \sin x\, dx,\quad \int_{a}^{\xi} \cos(\alpha x + \beta)\, dx \] はどれも \(\xi \to \infty\) で有限に振動する。
-
積分 \[ \int_{a}^{\xi} x\cos x\, dx,\quad \int_{a}^{\xi} x^{2}\sin x\, dx\quad \int_{a}^{\xi} x^{n} \cos(\alpha x + \beta)\, dx \] は \(\xi \to \infty\) で無限に振動する。ここで \(n\) は正の整数とする。
-
\(\bm{-\infty}\) への積分: 積分 \(\displaystyle\int_{\xi}^{a} \phi(x)\, dx\) が \(\xi \to -\infty\) で極限 \(l\) に向かうとする。このとき \(\displaystyle\int_{-\infty}^{a} \phi(x)\, dx\) は収束して \(l\) に等しいと言う。この積分は上で議論した無限積分と同様の性質を一つ残らず持つ。定式化は容易だろう。
-
\(\bm{-\infty}\) から \(\bm{+\infty}\) への積分: 積分 \[ \int_{-\infty}^{a} \phi(x)\, dx,\quad \int_{a}^{\infty} \phi(x)\, dx \] がどちらも収束して、その値が \(k,\ l\) だとする。このとき \[ \int_{-\infty}^{\infty} \phi(x)\, dx \] は収束し、その値は \(k + l\) であると言う。
-
次を示せ: \[ \int_{-\infty}^{0} \frac{dx}{1 + x^{2}} = \int_{0}^{\infty} \frac{dx}{1 + x^{2}} = \dfrac{1}{2} \int_{-\infty}^{\infty} \frac{dx}{1 + x^{2}} = \dfrac{1}{2}\pi \]
-
一般に \[ \int_{-\infty}^{\infty} \phi(x^{2})\, dx = 2\int_{0}^{\infty} \phi(x^{2})\, dx \] だと示せ。積分 \(\displaystyle\int_{0}^{\infty} \phi(x^{2})\, dx\) の収束を仮定してよい。
-
\(\displaystyle\int_{0}^{\infty} x\phi(x^{2})\, dx\) が収束するなら \(\displaystyle\int_{-\infty}^{\infty} x\phi(x^{2})\, dx = 0\) だと示せ。
-
§173 で触れたアーベルの定理の拡張: \(\phi(x)\) が常に正で単調減少なら、\(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) が収束するとき \(x\phi(x) \to 0\) が成り立つ。(a) アーベルの定理と積分判定法および (b) §173 と同様の直接的な議論の二つの方法で示せ。
-
\(a = x_{0} \lt x_{1} \lt x_{2} \lt \cdots\) かつ \(x_{n} \to \infty\) として、\(\displaystyle u_{n}= \int_{x_{n}}^{x_{n+1}} \phi(x)\, dx\) と定める。このとき \(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) は \(\sum u_{n}\) と同様に収束または発散する。\(\phi(x)\) が常に正なら逆も正しい。 [逆が一般に正しくないことは \(\phi(x) = \cos x,\ x_{n} = n\pi\) を考えれば分かる]