第六章 微分と積分
§110 導関数 (その 1)
曲線に自然に関連付けられる性質の議論に戻る。最も重要で明白な性質は、前章で見た、曲線の見た目がつながっているかどうかという性質である。この性質は連続関数の定義で表される。
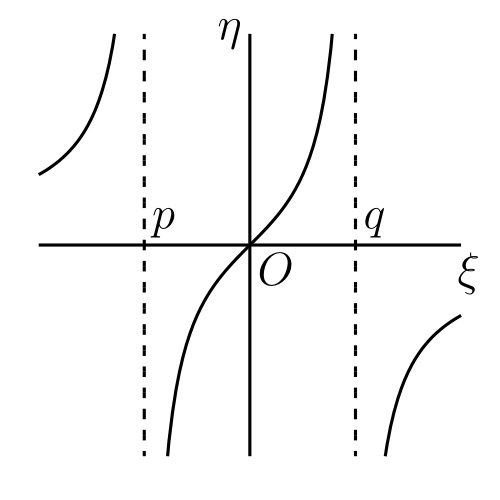
直線・円・円錐曲線といった初等幾何学で登場する普通の曲線には他にもたくさんの一般的な性質がある。その中でおそらく最も単純で最も注目に値するのは、曲線の各点で有限の方向が定まる、言い換えると、曲線上の各点で接線が引けることである。読者も知っての通り、初等幾何学では曲線上の点 \(P\) における接線が「点 \(Q\) が点 \(P\) に向かって近づくときの、弦 \(PQ\) の"極限"」として定義される。この「極限」の存在するという仮定が意味することを考えよう。
図 36 の \(P\) は曲線上の固定された点で、\(Q\) は移動する点だとする。\(PM, QN \) は \(OY\) と平行で、\(PR\) は \(OX\) と平行である。\(P\) の座標を \((x,\ y)\) として \(Q\) の座標を \((x + h,\ y + k)\) とすれば、\(N\) が \(M\) の左にあるとき \(h\) は正となり、右にあるとき負となる。

\(P\) で曲線の接線が存在すると仮定していた。つまり弦 \(PQ\) の「極限」が存在する。\(P\) における接線 \(PT\) と \(OX\) の角度を \(\psi\) とする。このとき \(PT\) が \(PQ\) の「極限」であるとは、曲線の両側から \(Q\) を \(P\) に近づけたときの \(\angle QPR\) の極限が \(\psi\) であることを意味する。ここで一般的なケースと例外的なケースを区別する必要がある。
\(\phi\) が \(\frac{1}{2}\pi\) でない一般的なケースでは、\(PT\) と \(OY\) が平行でない。そして \(\angle RPQ\) は極限 \(\psi\) に向かう。つまり \[ \frac{RQ}{PR} = \tan \angle RPQ \] は極限 \(\tan \psi\) に向かう。ここで \[ \frac{RQ}{PR} = \frac{NQ - MP}{MN} = \frac{\phi(x + h) - \phi(x)}{h} \] だから、 \[ \lim_{h \to 0} \frac{\phi(x + h) - \phi(x)}{h} = \tan\psi \qquad \text{(1)} \] が成り立つ。
ここまでの式が符号の影響を受ける点に注意してほしい。つまり \(Q\) が \(P\) に左にあるなら \(RQ\) は負となる。しかし (1) が表す極限の収束は \(h\) の符号に影響されない。
つまり \(\phi(x)\) のグラフとして表される曲線が点 \(P\) で \(x\) 軸と垂直でない接線を持つとすれば、\(\phi(x)\) は「\(P\) の横座標を \(x\) とすると、\(h\) が \(0\) に向かうとき \(\{\phi(x + h) - \phi(x)\}/h\) が極限に向かう」という性質を持つ。
もちろんこれは \(h\) が正の値だけを取って \(0\) に向かうときに
\[ \frac{\phi(x + h) - \phi(x)}{h},\quad \frac{\phi(x - h) - \phi(x)}{-h} \] の両方が存在し、二つの値が等しいことを意味する。もし二つの極限が存在して値が異なるなら、曲線 \(y = \phi(x)\) は点 \(P\) で角ついている (図 37)。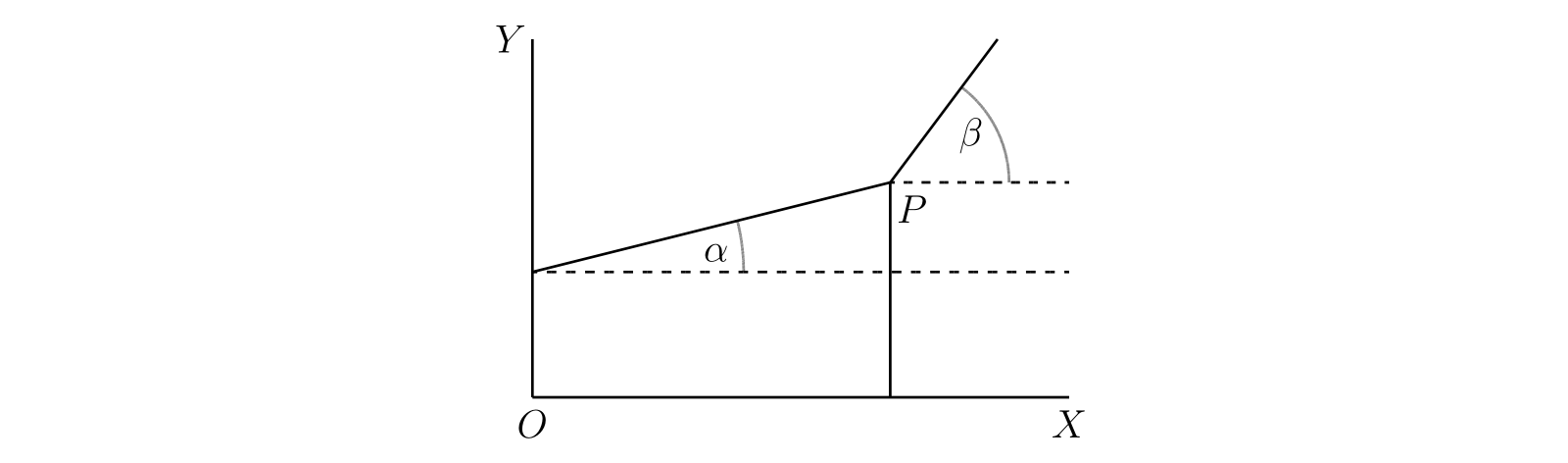
円や楕円のように曲線上の全ての点で接線が引ける、あるいは区間内の全ての \(x\) に対応するの点で接線が引けると仮定する。さらに接線が \(x\) 軸と垂直にならないとする。これにより例えば円を考えるときは半円よりも小さい弧を考えることになる。このとき式 \(\text{(1)}\) が区間内の全ての \(x\) で成り立つ。全ての \(x\) には対応する \(\tan \psi\) が存在するので、\(\tan \psi\) は \(x\) の関数となる。この関数は考えている全ての \(x\) に対して定義され、その値は元の関数 \(\psi(x)\) から計算・導出できる。この関数を導関数 (derivative, derived function) と呼び、次の記号で表す: \[ \phi'(x) \]
\(\phi(x)\) の導関数は \(\phi(x)\) の微分係数 (differential coefficient) とも呼ばれる。\(\phi(x)\) から \(\phi'(x)\) を求める操作を一般に微分 (differentiation) と呼ぶ。このような名前が付けられたのには歴史的な理由がある: §115 を見よ。
前述した例外では \(\psi = \frac{1}{2}\pi\) となる。この場合について詳しく考える前に、定義に関する注意や図を使った説明を行う。
§111 導関数 (その 2)
-
区間 \(a \leq x \leq b\) の全ての \(x\) で導関数 \(\phi'(x)\) が存在するなら、\(\phi(x)\) はその区間の全ての点で連続となる。なぜなら \(\{\phi(x + h) - \phi(x)\}/h\) が極限に向かうとき \(\lim\phi(x + h) = \phi(x)\) が成り立ち、連続性という言葉がこの性質を表すからである。
-
この逆も成り立つだろうか。つまり、任意の連続曲線の全ての点で接線が引けて、その点の \(x\) 座標における関数の微分係数が求まるだろうか1。もちろん答は「成り立たない」である。平行でない二つの直線から構成される関数を考えればよい (図 37)。直線の交点における \(\{\phi(x + h) - \phi(x)\}/h\) の極限を考えると、\(h\) が正の値から \(0\) に近づくときの極限は \(\tan \beta\) だが、負の値から近づくときの極限は \(\tan \alpha\) となる。
この場合には曲線がこの点で二つの傾きを持つと言えなくもない。しかし次の手の込んだ例を見れば、連続曲線の傾きが一つとも複数とも言えない場合があると分かるだろう。関数 \(x \sin(1/x)\) のグラフ (図 14) を考える。この関数は \(x = 0\) で定義されないので、\(x = 0\) で不連続となる。一方で \[ \begin{cases} \phi(x) = x\sin\dfrac{1}{x} & (x \neq 0),\\ \phi(x) = 0 & (x = 0) \end{cases} \] と定義される関数は \(x = 0\) で連続となる (例 37.14)。よってこの関数のグラフは連続曲線である。
しかし \(\phi(x)\) は \(x = 0\) で微分できない。定義から \(\phi'(x)\) は \(\lim\{\phi(h) - \phi(0)\}/h\) つまり \(\lim\sin(1/h)\) となるが、この極限は存在しない。
\(x\) の連続関数であって全ての \(x\) で微分できないものが存在することも示せるが、その証明はずっと難しい。この問題に興味がある読者はブロムウィッチ著 Infinite Series, pp. 490–1 およびホブソン著 Theory of Functions of a Real Variable, pp. 620–5 を参照してほしい。
-
導関数と微分係数は幾何学的な考察を通して導入されたが、その定義には幾何学的な要素が一切ない。つまり関数 \(\phi(x)\) の導関数 \(\phi'(x)\) を、\(\phi(x)\) の幾何学的表現と関係なしに \[ \phi'(x) = \lim_{h \to 0} \frac{\phi(x + h) - \phi(x)}{h} \] と定義して、特定の \(x\) でこの極限が存在するかに応じて \(\phi(x)\) が微分係数を持つあるいは持たないという言葉を定めても問題はない。曲線幾何学は導関数が利用される様々な数学分野の一つに過ぎない。
導関数が利用される重要な分野が動力学である。粒子が直線上を移動していて、時刻 \(t\) におけるとある固定点からの距離が \(s = \phi(t)\) だとする。このとき「時刻 \(t\) における粒子の速度」は定義より \[ \frac{\phi(t + h) - \phi(t)}{h} \] の \(h \to 0\) における極限となる。つまり「速度」という概念は関数の導関数の特殊な場合とみなせる。
-
\(\phi(x)\) が定数なら \(\phi'(x) = 0\) である。この結果を幾何学的に解釈せよ。
-
\(\phi(x) = ax + b\) なら \(\phi'(x) = a\) である。定義および幾何学的考察の両方からこれを示せ。
-
\(m\) が正の整数で \(\phi(x) = x^{m}\) なら \(\phi'(x) = mx^{m-1}\) である。
[次の式が成り立つ: \[ \begin{aligned} \phi'(x) & = \lim \frac{(x + h)^{m} - x^{m}}{h}\\ & = \lim \left\{mx^{m-1} + \frac{m(m - 1)}{1·2} x^{m-2} h + \cdots + h^{m-1}\right\} \end{aligned} \]
有理数 \(p/q\) に対する \(x^{p/q}\) ではこの方法を使えないことに注意してほしい。\((x + h)^{p/q}\) を \(h\) の指数が有限の級数で表す方法は存在しないからである。§118 ではこの結果が全ての有理数 \(m\) に対して正しいこと見る。ここでは \(m\) が特殊な有理数 (例えば \(\frac{1}{2}\)) である場合の \(\phi'(x)\) を個別に考えてみるとよい]
-
\(\phi(x) = \sin x\) なら \(\phi'(x) = \cos x\) で、\(\phi(x) = \cos x\) なら \(\phi'(x) = -\sin x\) である。
[\(\phi(x) = \sin x\) なら次が成り立つ: \[ \frac{\phi(x + h) - \phi(x)}{h} = \frac{2\sin \dfrac{1}{2}h \cos(x + \dfrac{1}{2}h)}{h} \] \(\lim\cos(x + \frac{1}{2}h) = \cos x\) (\(\cos x\) は連続関数) と \(\lim\{(\sin \frac{1}{2}h)/\frac{1}{2}h\} = 1\) (例 36.13) から、この式の \(h \to 0\) における極限が \(\cos x\) だと分かる]
-
曲線 \(y = \phi(x)\) の接線と法線の方程式: 曲線上の点 \((x_{0}, y_{0})\) における接線は \((x_{0}, y_{0})\) を通って \(OX\) との角度が \(\psi\) となる直線であり、\(\tan \psi = \phi'(x_{0})\) が成り立つ。よってその方程式は \[ y - y_{0} = (x - x_{0}) \phi'(x_{0}) \] となり、法線 (交点を通る接線と垂直な直線) の方程式は \[ (y - y_{0}) \phi'(x_{0}) + x - x_{0} = 0 \] となる。今は接線が \(y\) 軸と平行でないと仮定しているが、この例外的な場合には接線と法線がそれぞれ \(x = x_{0}\) と \(y = y_{0}\) になる。
-
放物線 \(x^{2} = 4ay\) 上の任意の点における接線と法線の方程式を求めよ。\(x_{0} = 2a/m\) かつ \(y_{0} = a/m^{2}\) なら \((x_{0}, y_{0})\) における接線が \(x = my + (a/m)\) となることを示せ。
§112 導関数 (その 3)
\(\phi(x)\) が不連続となる \(x\) では \(\phi(x)\) に微分係数が存在しないことを見た。例えば \(1/x\) や \(\sin(1/x)\) のような \(x = 0\) で定義されない関数は当然 \(x = 0\) で不連続なので、\(x = 0\) における微分係数を持たない。あるいは \([x]\) は任意の整数の \(x\) で不連続なので、整数の \(x\) 全てで微分できない。
\([x]\) は連続する二つの整数の間で定数なので、微分が存在する場所では常に \(0\) となる。よって \([x]\) の微分 \([x]'\) は整数では定義されず、それ以外では \(0\) と等しい関数となる。興味深いことに、関数 \(1 - \dfrac{\sin\pi x}{\sin\pi x}\) も全く同じ性質を持っている。
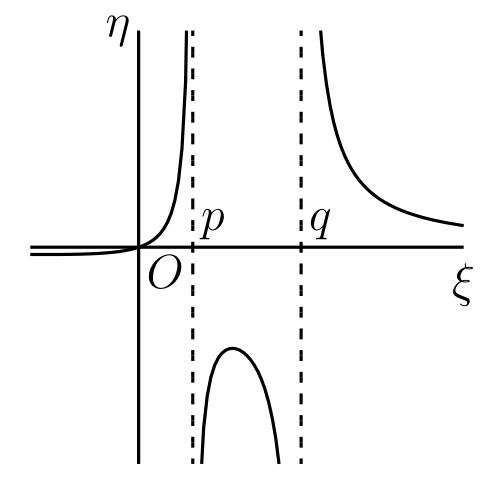
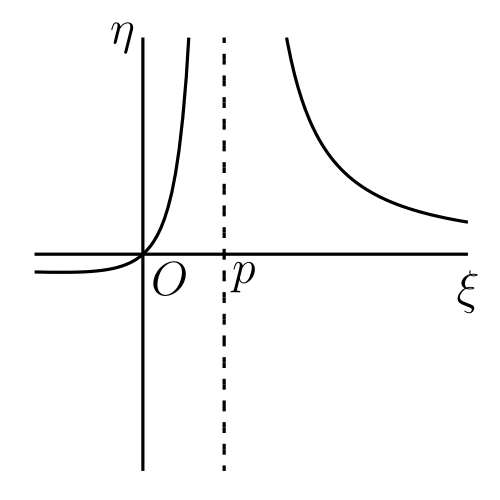
例 37.7 で触れた通り、多項式・有理関数・三角関数といった最も単純で簡単な種類の関数では、不連続性はたいてい \[ \phi(x) \to +\infty \] あるいは \(\phi(x) \to -\infty\) のときに生じる。いずれの場合でも、関数はその \(x\) で微分係数を持たない。実は §111 の (1) からは \(\bm{\phi(x)}\) が不連続な点では \(\bm{\phi'(x)}\) も不連続になることが分かる。ただしこの逆は正しくない。これは §110 の幾何学的な考察に戻り、これまで考えてこなかった \(\phi(x)\) のグラフが \(OY\) と平行になる場合を考えればすぐに分かる。この場合には様々な状況が考えられるが、典型的な状況を 図 38 に示す。\(\text{(c)}\) と \(\text{(d)}\) では \(P\) の片側で関数が二つの値を取り、もう片側では定義されない。このような場合には \(\phi(x)\) を \(P\) で分けて、二つの関数 \(\phi_{1}(x)\) と \(\phi_{2}(x)\) を考えることができる (上側を \(\phi_{1}(x)\) とする)。

\(h \to 0\) のとき、\(\text{(a)}\) では \[ \frac{\phi(x + h) - \phi(x)}{h} \to +\infty \] であり、\(\text{(b)}\) では \[ \frac{\phi(x + h) - \phi(x)}{h} \to -\infty \] となる。一方 \(\text{(c)}\) では \[ \frac{\phi_{1}(x + h) - \phi_{1}(x)}{h} \to +\infty,\quad \frac{\phi_{2}(x + h) - \phi_{2}(x)}{h} \to -\infty \] であり、\(\text{(d)}\) では \[ \frac{\phi_{1}(x + h) - \phi_{1}(x)}{h} \to -\infty,\quad \frac{\phi_{2}(x + h) - \phi_{2}(x)}{h} \to +\infty \] となる。もちろん \(\text{(c)}\) と \(\text{(d)}\) では正の \(h\) だけを考え、\(\text{(d)}\) では負の \(h\) だけを考えるとする。なお正負両方の \(h\) を考えられないという事実さえあれば微分係数が存在しないことを結論できる。
四つのケースは次の方程式で定義される関数から得られる: \[ \text{(a)}\ y^{3} = x,\quad \text{(b)}\ y^{3} = -x,\quad \text{(c)}\ y^{2} = x,\quad \text{(d)}\ y^{2} = -x \] 考えるべき特別な \(x\) の値は \(x = 0\) である。
§113 微分の一般的性質
この節の命題では、考えている \(x\) において \(f(x)\) と \(F(x)\) に \(f'(x)\) と \(F'(x)\) という導関数が存在すると仮定する。
\(\phi(x) = f(x) + F(x)\) なら、\(\phi(x)\) の導関数は \[ \phi'(x) = f'(x) + F'(x) \] となる。
\(\phi(x) = kf(x)\) で \(k\) が定数なら、\(\phi(x)\) の導関数は \[ \phi'(x) = kf'(x) \] となる。
例 35.1 の定理からこの二つの結果を導くのは読者への練習問題とする。
\(\phi(x) = f(x)F(x)\) なら、\(\phi(x)\) の導関数は \[ \phi'(x) = f(x)F'(x) + f'(x)F(x) \] となる。
次の等式から示せる: \[ \begin{aligned} \phi'(x) & = \lim\frac{f(x + h)F(x + h) - f(x)F(x)}{h}\\ & = \lim\left\{f(x + h)\frac{F(x + h) - F(x)}{h} + F(x)\frac{f(x + h) - f(x)}{h}\right\}\\ & =f(x)F'(x) + F(x)f'(x) \end{aligned} \]
\(\phi(x) = \dfrac{1}{f(x)}\) なら、\(\phi(x)\) の導関数は \[ \phi'(x) = -\frac{f'(x)}{\{f(x)\}^{2}} \] となる。
もちろんこの命題では考えている \(x\) で \(f(x)\) が \(0\) にならないと仮定する。この仮定の下で \[ \phi'(x) = \lim \frac{1}{h} \left\{\frac{f(x) - f(x + h)}{f(x + h)f(x)}\right\} = -\frac{f'(x)}{\{f(x)\}^{2}} \] が成り立つ。
\(\phi(x) = \dfrac{f(x)}{F(x)}\) なら、\(\phi(x)\) の導関数は \[ \phi'(x) = \frac{f'(x)F(x) - f(x)F'(x)}{\{F(x)\}^{2}} \] となる。
これは結果 3 と結果 4 から直ちに従う。
\(\phi(x) = F\{f(x)\}\) なら、\(\phi(x)\) の導関数は \[ \phi'(x) = F'\{f(x)\} f'(x) \] となる。
証明は次の通り。 \[ f(x) = y,\quad f(x + h) = y + k \] とすると、\(h \to 0\) のとき \(k \to 0\) および \(k/h \to f'(x)\) が成り立つ。よって \[ \begin{aligned} \phi'(x) & = \lim \frac{F\{f(x + h)\} - F\{f(x)\}}{h}\\ & = \lim \left\{\frac{F(y + k) - F(y)}{k}\right\} × \lim \left(\frac{k}{h}\right)\\ & = F'(y)f'(x) \end{aligned} \] が分かる。
\(F(x) = kx\) および \(F(x) = 1/x\) とすれば結果 2 と結果 4 が得られる。また \(f(x) = ax + b\) としても興味深い関係が得られる: \(F(ax + b)\) の導関数は \(aF'(ax + b)\) である。
最後の命題には少し説明がいる。\(x = \psi(y)\) で、とある \(y\) の区間で \(\psi(y)\) が連続かつ狭義単調増加もしくは狭義単調減少 (§95) だとする。このとき \(\psi\) の「逆関数」 \(y = \phi(x)\) が存在する (§109)。
\(\phi\) が \(\psi\) の逆関数で、\(y = \phi(x)\) および \(x = \psi(y)\) とする。\(\psi(y)\) の導関数が \(\psi'(y)\) で \(0\) でないなら、\(\phi(x)\) の導関数は \[ \phi'(x) = \frac{1}{\psi'(y)} \] となる。
\(\phi(x + h) = y + k\) とすると \(k \to 0\) のとき \(h \to 0\) であり、 \[ \begin{aligned} \phi'(x) & = \lim_{h \to 0} \frac{\phi(x + h) - \phi(x)}{(x + h) - x} \\ & = \lim_{k \to 0} \frac{(y + k) - y}{\psi(y + k) - \psi(y)} \\ & = \frac{1}{\psi'(y)} \end{aligned} \] が成り立ことから示せる。最後の結果は関係 \(y = \phi(x)\) を使って \(\phi'(x) = 1/\psi'\{\phi(x)\}\) という \(x\) を使った形に書き直せる。つまりこの結果は逆関数の微分が分かっている関数の微分を可能にする。
§114 複素関数の導関数
ここまでは \(y = \phi(x)\) が \(x\) の実関数だとしてきた。\(y\) が複素関数 \(\phi(x) + i\psi(x)\) なら、\(y\) の微分を \(\phi'(x) + i\psi'(x)\) と定義できる。複素関数 \(\phi(x)\) に対する前節の結果 1 から 5 は簡単に確認できるだろう。結果 6 と 7 にも複素関数に対する似た命題が存在するが、この命題の拡張には「複素変数の関数」の一般的な概念が必要となる。この概念はこれまでに特殊な例として数回だけしか登場していない。
§115 微分の記法
導関数 (derivative) が微分係数 (differential coefficient) という別名を持つと前に説明したが、違う名前だけでなく違う記号も存在する。関数 \(y = \phi(x)\) の導関数を指して \[ D_{x}y,\quad \frac{dy}{dx} \] と表記する場合もある。最後の記号が理解しやすいということで一番よく使われる。ここで \(dy/dx\) の意味が「実数 \(dy\) を実数 \(dx\) で割った数」でない点に注意する必要がある。\(dy/dx\) は「\(D_{x}\) あるいは \(d/dx\) で表される操作を \(y = f(x)\) に適用した結果」を意味する。つまり \(D_{x}\) と \(d/dx\) は \(h \to 0\) における \(\{\phi(x + h) - \phi(x)\}/h\) の極限を取る操作を表す。
但し書きが必要なほど分かりにくい \(d/dy\) という記号が使われているのには理由がある。\(\{\phi(x + h) - \phi(x)\}/h\) の分母 \(h\) は独立変数 \(x\) の値 \(x + h\) と \(x\) の差異であり、分子は従属変数 \(y\) の値 \(\phi(x + h)\) と \(\phi(x)\) の差異である。これらの差異はそれぞれ \(x\) と \(y\) の増分 (increments) と呼ばれ、\(\delta x\) および \(\delta y\) と表記される。すると \(x\) と \(y\) の増分の比は \(\delta y/\delta x\) であり、その極限を \(dy/dx\) と表記すると様々な用途で便利なことが分かっている。もちろんこの極限は \(\phi'(x)\) と等しいが、今の段階では、\(dx/dy\) を一つの記号とみなさなければならない。つまり \(dy\) と \(dx\) を切り離して考えることはできず、\(dx\) あるいは \(dy\) と書いたところで意味を持たない。特に \(dy\) と \(dx\) は \(\lim \delta y\) や \(\lim \delta x\) を意味しない: この極限は常に \(0\) に等しい。いずれはこの記法に慣れる必要があるが、それまでは微分係数の表記に \(D_{x}y\) あるいはこれまでと同様に \(\phi'(x)\) を使った方がよいかもしれない。
一方で第七章では、\(dy/dx\) が実際に \(dx\) と \(dy\) の比となるように \(dx\) と \(dy\) という記号を別々に定義できることを示す。
もちろん §113 の定理はこの記法を使って次のように表せる:
-
\(y = y_{1} + y_{2}\) なら \[ \frac{dy}{dx} = \frac{dy_{1}}{dx} + \frac{dy_{2}}{dx} \]
-
\(y = ky_{1}\) なら \[ \frac{dy}{dx} = k\frac{dy_{1}}{dx} \]
-
\(y = y_{1}y_{2}\) なら \[ \frac{dy}{dx} = y_{1}\frac{dy_{2}}{dx} + y_{2}\frac{dy_{1}}{dx} \]
-
\(y = \dfrac{1}{y_{1}}\) なら \[ \frac{dy}{dx} = -\frac{1}{y_{1}^{2}}\, \frac{dy_{1}}{dx} \]
-
\(y = \dfrac{y_{1}}{y_{2}}\) なら \[ \frac{dy}{dx} = \biggl(y_{2}\frac{dy_{1}}{dx} - y_{1}\frac{dy_{2}}{dx}\biggr) \bigg/ y_{2}^{2} \]
-
\(y\) が \(x\) の関数で \(y\) が \(z\) の関数なら \[ \frac{dz}{dx} = \frac{dz}{dy}\, \frac{dy}{dx} \]
-
\(\dfrac{dy}{dx} = 1 \bigg/ \biggl(\dfrac{dx}{dy}\biggr)\)
-
\(y = y_{1}y_{2}y_{3}\) なら \[ \frac{dy}{dx} = y_{2}y_{3}\, \frac{dy_{1}}{dx} + y_{3}y_{1}\, \frac{dy_{2}}{dx} + y_{1}y_{2}\, \frac{dy_{3}}{dx} \] であり、\(y = y _{1}y_{2} \cdots y_{n}\) なら \[ \frac{dy}{dx} = \sum_{r=1}^{n} y_{1}y_{2} \cdots y_{r-1}y_{r+1} \cdots y_{n}\, \frac{dy_{r}}{dx} \] となる。特に \(y = z^{n}\) とすると \(dy/dx = nz^{n-1}(dz/dx)\) が分かる。また \(y = x^{n}\) とすれば 例 39.3 で証明した \(dy/dx = nx^{n-1}\) が示せる。
-
\(y = y_{1}y_{2}\cdots y_{n}\) なら \[ \frac{1}{y}\, \frac{dy}{dx} = \frac{1}{y_{1}}\, \frac{dy_{1}}{dx} + \frac{1}{y_{2}}\, \frac{dy_{2}}{dx} + \cdots + \frac{1}{y_{n}}\, \frac{dy_{n}}{dx} \] が成り立つ。特に \(y = z^{n}\) なら \(\dfrac{1}{y}\, \dfrac{dy}{dx} = \dfrac{n}{z}\, \dfrac{dz}{dx}\) となる。
§116 多項式の微分
続いて単純な種類の関数の微分についてさらに体系的に見ていく。
-
多項式: \(\phi(x) = a_{0}x^{n} + a_{1}x^{n-1} + \cdots + a_{n}\) なら、 \[ \phi'(x) = na_{0}x^{n-1} + (n - 1)a_{1}x^{n-2} + \cdots + a_{n-1} \] が成り立つ。\(x\) の \(n\) 次方程式をいわゆる二項形式 (binomial form) で表した方が分かりやすい場合もある: \[ a_{0}x^{n} + \binom{n}{1} a_{1}x^{n-1} + \binom{n}{2} a_{2}x^{n-2} + \cdots + a_{n} \] このときは \[ \phi'(x) = n \left\{ a_{0}x^{n-1} + \binom{n - 1}{1} a_{1}x^{n-2} + \binom{n - 1}{2} a_{2}x^{n-3} + \cdots + a_{n-1} \right\} \] となる。
\(\phi(x)\) の二項形式が \[ (a_{0}, a_{1},\ \ldots, a_{n} \mathbin{)\kern-5pt(} x, 1)^{n} \] と表記されることもある。この表記を使えば \[ \phi'(x) = n(a_{0}, a_{1},\ \ldots, a_{n-1} \mathbin{)\kern-5pt(} x, 1)^{n-1} \] である。
後で示すように、\(\phi(x)\) は必ず \(n\) 個の因数の積として次のように書ける: \[ \phi(x) = a_{0}(x - \alpha_{1})(x - \alpha_{2}) \cdots (x - \alpha_{n}) \] ここで \(\alpha_{\ast}\) は実数または複素数を表す。このとき \[ \phi'(x) = a_{0}\sum (x - \alpha_{1}) \cdots (x - \alpha_{k-1}) (x - \alpha_{k+1}) \cdots (x - \alpha_{n}) \] となる。つまり \(n - 1\) 個の因数の積を全て足せば微分が得られる。この形の結果は \(\alpha\) のいくつかが等しい場合でも成り立つ。ただしその場合には等しい \(\alpha\) の分だけ右辺の因数を反復する。つまり \[ \phi(x) = a_{0}(x - \alpha_{1})^{m_{1}} (x - \alpha_{2})^{m_{2}}\cdots (x - \alpha_{\nu})^{m_{\nu}} \] が \[ \phi'(x) = a_{0} \sum m_{k} (x - \alpha_{1})^{m_{1}-1} \cdots (x - \alpha_{k-1})^{m_{k-1}} (x - \alpha_{k+1})^{m_{k+1}} \cdots (x - \alpha_{\nu})^{m_{\nu}} \] となる。
-
\(\phi(x)\) が多項式なら、\(\phi'(x)\) が \(\phi(x + h)\) を展開した式における \(h\) の係数だと示せ。
-
\(\phi(x)\) が \((x - \alpha)^{2}\) で割り切れるなら、\(\phi'(x)\) は \((x - \alpha)\) で割り切れる。一般に \(\phi(x)\) が \((x - \alpha)^{m}\) で割り切れるなら、\(\phi'(x)\) は \((x - \alpha)^{m-1}\) で割り切れる。
-
逆に \(\phi(x)\) と \(\phi'(x)\) が両方とも \(x - \alpha\) で割り切れるなら、\(\phi(x)\) は \((x - \alpha)^{2}\) で割り切れる。そして \(\phi(x)\) と \(\phi'(x)\) が両方とも \((x - \alpha)^{m-1}\) で割り切れるなら、\(\phi(x)\) は \((x - \alpha)^{m}\) で割り切れる。
-
多項式 \(P(x) = 0\) について、\(P(x) = 0\) の重根とその重複度を可能な限り完全に求める方法を示せ。初等代数的な操作だけを使うこと。
[\(H_{1}\) を \(P\) と \(P'\) の最大公約数として、\(H_{2}\) を \(H_{1}\) と \(P''\) の最大公約数、\(H_{3}\) を \(H_{2}\) と \(P'''\) の最大公約数 \(\cdots\) と以下同様に定める。すると \(H_{1}H_{3}/H_{2}^{2} = 0\) の根が \(P = 0\) の二重根、\(H_{2}H_{4}/H_{3}^{2}\) の根は \(P = 0\) の 三重根 \(\cdots\) となる。ただし \(H_{1}H_{3}/H_{2}^{2} = 0,\ H_{2}H_{4}/H_{3}^{2} = 0,\ \ldots\) の根を代数的に求められるとは限らない。例えば \(P(x) = (x - 1)^{3}(x^{5} - x - 7)^{2}\) だと \(H_{1}H_{3}/H_{2}^{2} = x^{5} - x - 7\) および \(H_{2}H_{4}/H_{3}^{2} = x - 1\) となるが、一つ目の式は代数的に解くことができない]
-
次の方程式の根とその重複度を求めよ: \[ \begin{gathered} x^{4} + 3x^{3} - 3x^{2} - 11x - 6 = 0,\\ x^{6} + 2x^{5} - 8x^{4} - 14x^{3} + 11x^{2} + 28x + 12 = 0 \end{gathered} \]
-
\(ax^{2} + 2bx + c\) が重根を持つ、つまり \(a(x - \alpha)^{2}\) という形に変形できるなら、\(2(ax + b)\) が \(x - \alpha\) で割り切れる。よって \(\alpha = -b/a\) である。さらに \(x = \alpha\) は \(ax^{2} + 2bx + c = 0\) を満たす。最終的に得られる条件が \(ac - b^{2} = 0\) だと示せ。
-
方程式 \(\dfrac{1}{x - a} + \dfrac{1}{x - b} + \dfrac{1}{x - c} = 0\) は \(a = b = c\) のときに限って二重根を持つ。
(Math. Trip. 1905.)
-
方程式 \[ ax^{3} + 3bx^{2} + 3cx + d = 0 \] が \(G^{2} + 4H^{3} = 0\) のとき二つの根を持つことを示せ。ここで \(H = ac - b^{2}\) および \(G = a^{2}d - 3abc + 2b^{3}\) とする。
[方程式に \(ax + b = y\) を代入すると \(y^{3} + 3Hy + G = 0\) となる。これは \(y^{2} + H = 0\) と同じ根を持つ]
-
\(\alpha,\ \beta,\ \gamma,\ \delta\) を \[ ax^{4} + 4bx^{3} + 6cx^{2} + 4dx + e = 0 \] の根とする。このとき \[ \dfrac{1}{12}a \{ (\alpha - \beta)(\gamma - \delta) - (\gamma - \alpha)(\beta - \delta) \} \] および \(\alpha,\ \beta,\ \gamma\) を循環させた三つの値を根に持つ方程式は \[ 4\theta^{3} - g_{2}\theta - g_{3} = 0 \] である。ここで \[ \begin{aligned} g_{2} & = ae - 4bd + 3c^{2},\\ g_{3} & = ace + 2bcd - ad^{2} - eb^{2} - c^{3} \end{aligned} \] とする。\(\alpha,\ \beta,\ \gamma,\ \delta\) のどれか二つが等しいときこの三次方程式の根の二つが等しくなる。さらに問題 8 から \(g_{2}^{3} - 27g_{3}^{2} = 0\) が分かる。
-
\(\phi(x)\) が多項式なら、任意の \(\phi(x) = 0\) の根の組の間に \(\phi'(x) = 0\) の根がある。
多項式に限らない一般的な関数のクラスに対するこの定理の証明は後で示す。ここで示すのは多項式のみに適用できる代数的な証明である。\(\alpha,\ \beta\) を隣り合う二つの根として、その重複度を \(m,\ n\) とする。このとき多項式 \(\theta(x)\) を使って \[ \phi(x) = (x - \alpha)^{m} (x - \beta)^{n} \theta(x) \] と表せば、\(\theta(x)\) は \(\alpha \leq x \leq \beta\) で同じ符号を持つ。このとき \[ \small\begin{aligned} \phi'(x) & = (x - \alpha)^{m} (x - \beta)^{n} \theta'(x) \\ & \qquad + \{m(x - \alpha)^{m-1} (x - \beta)^{n} + n(x - \alpha)^{m} (x - \beta)^{n-1}\} \theta(x)\\ & = (x - \alpha)^{m-1} (x - \beta)^{n-1} [(x - \alpha) (x - \beta) \theta'(x) + \{m(x - \beta) + n(x - \alpha)\} \theta(x)]\\ & = (x - \alpha)^{m-1} (x - \beta)^{n-1} F(x) \end{aligned} \] とすれば、\(F(\alpha) = m(\alpha - \beta) \theta(\alpha)\) と \(F(\beta) = n(\beta - \alpha) \theta(\beta)\) は逆の符号を持つ。よって \(F(x)\) および \(\phi'(x)\) は \(\alpha\) と \(\beta\) のどこかの \(x\) で \(0\) になる。
§117 有理関数の微分
-
有理関数: もし \[ R(x) = \frac{P(x)}{Q(x)} \] で \(P\) と \(Q\) が多項式なら、§113 の結果 5 から \[ R'(x) = \frac{P'(x)Q(x) - P(x)Q'(x)}{\{Q(x)\}^{2}} \] が分かる。この式を使えば任意の有理関数の導関数を計算できるが、最も単純な形が得られるとは限らない。最も単純な形になるのは \(Q(x)\) と \(Q'(x)\) が共通因数を持たないとき、つまり \(Q(x)\) が重複する因数を持たないときである。\(Q(x)\) が重複する因数を持つなら、この形で計算した \(R'(x)\) はさらに簡略化できる。
有理関数の微分では部分分数分解を利用できる場合が非常に多い。§116 と同様に \(Q(x)\) を \[ a_{0}(x - \alpha_{1})^{m_{1}} (x - \alpha_{2})^{m_{2}}\cdots (x - \alpha_{\nu})^{m_{\nu}} \] と表す。すると代数の文献2にあるように、多項式 \(\Pi(x)\) を前に出した次の形で \(R(x)\) を表せる: \[ \begin{aligned} \Pi(x) & + \frac{A_{1, 1}}{x - \alpha_{1}} + \frac{A_{1, 2}}{(x - \alpha_{1})^{2}} + \cdots + \frac{A_{1, m_{1}}}{(x - \alpha_{1})^{m_{1}}}\\ & + \frac{A_{2, 1}}{x - \alpha_{2}} + \frac{A_{2, 2}}{(x - \alpha_{2})^{2}} + \cdots + \frac{A_{2, m_{2}}}{(x - \alpha_{2})^{m_{2}}} + \cdots \end{aligned} \] これは一つの多項式と次の形をした項の和からなる: \[ \frac{A}{(x - \alpha)^{p}} \] ここで \(\alpha\) は \(Q(x) = 0\) の根である。多項式の微分方法は分かっているので、後は §113 の結果 (\(\alpha\) が複素数なら §114 で拡張した結果) を使えば分数の項の微分が \[ -\frac{pA(x -\alpha)^{p-1}}{(x - \alpha)^{2p}} = -\frac{pA}{(x - \alpha)^{p+1}} \] だと分かる。
よって一般的な有理関数 \(R(x)\) の微分は \[ \Pi'(x) - \frac{A_{1, 1}}{(x - \alpha_{1})^{2}} - \frac{2A_{1, 2}}{(x - \alpha_{1})^{3}} - \cdots - \frac{A_{2, 1}}{(x - \alpha_{2})^{2}} - \frac{2A_{2, 2}}{(x - \alpha_{2})^{3}} - \cdots \] という形で書ける。ちなみにこの結果からは \(\bm{m}\) の正負に関わらず \(\bm{x^{m}}\) の微分は \(\bm{mx^{m-1}}\) であることが導ける。
この節で説明した手法は有理関数を複数回微分するときに特に便利となる (例 45 を参照)。
-
次を示せ: \[ \frac{d}{dx}\left(\frac{x}{1 + x^{2}}\right) = \frac{1 - x^{2}}{(1 + x^{2})^{2}},\quad \frac{d}{dx}\left(\frac{1 - x^{2}}{1 + x^{2}}\right) = -\frac{4x}{(1 + x^{2})^{2}} \]
-
次を示せ: \[ \frac{d}{dx}\left(\frac{ax^{2} + 2bx + c}{Ax^{2} + 2Bx + C}\right) = \frac{(ax + b) (Bx + C) - (bx + c) (Ax + B)}{(Ax^{2} + 2Bx + C)^{2}} \]
-
\(Q\) が \((x - \alpha)^{m}\) を因数を持つとき \(R'\) の分母は \((x - \alpha)^{m+1}\) で割り切れるが、\(m + 1\) より大きい \(x - \alpha\) のべきでは割り切れない。
-
\(R'\) の分母が一次の因数 \(x - \alpha\) を持つことはない。よって、分母に一次の因数を含む任意の有理関数 (例えば \(1/x\)) は他の有理関数の導関数にならない。
§118 代数関数の微分
-
代数関数: 前節の結果と §113 の結果 6 を合わせれば、任意の陽な代数関数の導関数を得られる。
そのような関数の中で一番重要なのは、有理数 \(m\) に対する \(x^{m}\) である。正または負の整数の \(m\) に対しては \(x^{m}\) の微分が \(mx^{m-1}\) となることは §117 で前に見た。\(m\) が有理数のときにもこれが正しいことを示そう。整数 \(p,\ q\) を使って \(y = x^{m} = x^{p/q}\) とする。さらに \(z = x^{1/q}\) とすると \(x = z^{q}\) および \(y = z^{p}\) が成り立つ。よって \[ \frac{dy}{dx} = \biggl(\frac{dy}{dz}\biggr) \bigg/ \biggl(\frac{dx}{dz}\biggr) = \frac{p}{q} z^{p-q} = mx^{m-1} \] となる。
この結果は 例 36.3 を使っても示せる: \(\phi(x) = x^{m}\) とすれば \[ \begin{aligned} \phi'(x) & = \lim_{h \to 0} \frac{(x + h)^{m} - x^{m}}{h}\\ & = \lim_{\xi \to x} \frac{\xi^{m} - x^{m}}{\xi - x} = mx^{m-1} \end{aligned} \] であり、一般的な形の \[ \frac{d}{dx} (ax + b)^{m} = ma(ax + b)^{m-1} \] も任意の \(m\) に対して成り立つと分かる。
陰な代数関数の微分は理論的に難しい部分があるので、第七章でまた考える。ただし微分の計算自体は難しくない。次の例を見れば理解できるだろう。\(y\) を \[ x^{3} + y^{3} - 3axy = 0 \] とする。両辺を \(x\) で微分すると \[ x^{2} + y^{2} \frac{dy}{dx} - a\left(y + x \frac{dy}{dx}\right) = 0 \] を得る。これを変形すれば \[ \frac{dy}{dx} = -\frac{x^{2} - ay}{y^{2} - ax} \] となる。
-
次の関数の導関数を求めよ: \[ \sqrt{\frac{1 + x}{1 - x}},\quad \sqrt{\frac{ax + b}{cx + d}},\quad \sqrt{\frac{ax^{2} + 2bx + c}{Ax^{2} + 2Bx + C}},\quad (ax + b)^{m} (cx + d)^{n} \]
-
次を示せ: \[ \frac{d}{dx}\left\{\frac{x}{\sqrt{a^{2} + x^{2}}}\right\} = \frac{a^{2}}{(a^{2} + x^{2})^{3/2}},\quad \frac{d}{dx}\left\{\frac{x}{\sqrt{a^{2} - x^{2}}}\right\} = \frac{a^{2}}{(a^{2} - x^{2})^{3/2}} \]
-
次の関係が成り立つときの \(y\) の微分係数を求めよ: \[ \begin{aligned} & \,\text{(i)}\quad ax^{2} + 2hxy + by^{2} + 2gx + 2fy + c = 0,\\ & \text{(ii)}\quad x^{5} + y^{5} - 5ax^{2}y^{2} = 0 \end{aligned} \]
§119 超越関数の微分
-
超越関数: 例 39.4 では \[ D_{x} \sin x = \cos x, \quad D_{x} \cos x = -\sin x \] が成り立つことを見た。
また §113 の結果 4 と 5 を使えば \[ \begin{alignedat}{2} D_{x} \tan x & = \sec^{2} x, & D_{x} \cot x & = -\cosec^{2} x,\\ D_{x} \sec x & = \tan x \sec x, \quad & D_{x} \cosec x & = -\cot x\cosec x. \end{alignedat} \] を容易に確認できる。さらに結果 7 からは初等三角関数の逆関数の導関数が分かる。次の結果が得られるだろう: \[ \begin{alignedat}{2} D_{x} \arcsin x & = ±\frac{1}{\sqrt{1 - x^{2}}}, & D_{x} \arccos x & = \mp \frac{1}{\sqrt{1 - x^{2}}},\\ D_{x} \arctan x & = \frac{1}{1 + x^{2}}, & D_{x} \text{arccot } x & = -\frac{1}{1 + x^{2}},\\ D_{x} \text{arcsec } x & = ± \frac{1}{x\sqrt{x^{2} - 1}}, \quad & D_{x} \text{arccosec } x & = \mp \frac{1}{x\sqrt{x^{2} - 1}} \end{alignedat} \] ここでサインとコセカントの逆関数の符号は \(\cos(\arcsin x)\) と同じように取り、サインとセカントの逆関数の符号は \(\sin(\arccos x)\) と同じように取る。
さらに一般化した公式 \[ D_{x} \arcsin\frac{x}{a} = ±\frac{1}{\sqrt{a^{2} - x^{2}}},\quad D_{x} \arctan\frac{x}{a} = \frac{a}{x^{2} + a^{2}} \] も非常に重要であり、これは §113 の結果 7 を使って容易に導ける。ただし最初の式では符号を \(a\cos\{\arcsin(x/a)\}\) と同じように取る。なぜなら \[ a\sqrt{1 - \frac{x^{2}}{a^{2}}} = ±\sqrt{a^{2} - x^{2}} \] の符号が \(a\) の符号と一致するからである。
この例では \(m\) が有理数で、\(a,\ b,\ \ldots,\ \alpha,\ \beta,\ \ldots\) は考えている関数が実数になる値とする。
-
次の関数の導関数を求めよ: \[ \begin{gathered} \cos^{m} x, \quad \sin^{m} x, \quad \cos x^{m}, \\ \sin x^{m}, \quad \cos (\sin x), \quad \sin (\cos x),\\ \sqrt{a^{2}\cos^{2} x + b^{2}\sin^{2} x}, \quad \frac{\cos x\sin x}{\sqrt{a^{2}\cos^{2} x + b^{2}\sin^{2} x}},\\ x\arcsin x + \sqrt{1 - x^{2}}, \quad (1 + x)\arctan\sqrt{x} - \sqrt{x} \end{gathered} \]
-
\(0\) から \(1\) の \(x\) に対して \(\arcsin x + \arccos x\) が定数であること、および全ての \(x\) に対して \(\text{arctan } x + \text{arccot } x\) が定数であることを微分を使って確かめよ。
-
次の関数の導関数を求めよ: \[ \arcsin\sqrt{1 - x^{2}},\quad \arcsin\{2x\sqrt{1 - x^{2}}\},\quad \arctan \left(\frac{a + x}{1 - ax}\right) \] 答えの単純さをどう説明できるか?
-
次の関数を微分せよ: \[ \frac{1}{\sqrt{ac - b^{2}}} \arctan \frac{ax + b}{\sqrt{ac - b^{2}}},\quad -\frac{1}{\sqrt{-a}} \arcsin\frac{ax + b}{\sqrt{b^{2} - ac}} \]
-
関数 \[ 2\arcsin \sqrt{\frac{x - \beta}{\alpha - \beta}},\quad 2\arctan \sqrt{\frac{x - \beta}{\alpha - x}},\quad \arcsin \frac{2\sqrt{(\alpha - x)(x - \beta)}}{\alpha - \beta} \] がどれも \[ \frac{1}{\sqrt{(\alpha - x)(x - \beta)}} \] を導関数に持つことを示せ。
-
次を示せ: \[ \frac{d}{d\theta}\left\{ \arccos \sqrt{\frac{\cos 3\theta}{\cos^{3}\theta}} \right\} = \sqrt{\frac{3}{\cos\theta \cos 3\theta}} \]
(Math. Trip. 1904.)
-
次を示せ: \[ \frac{1}{\sqrt{C(Ac - aC)}}\, \frac{d}{dx} \left[ \arccos \sqrt{\frac{C(ax^{2} + c)}{c(Ax^{2} + C)}} \right] = \frac{1}{(Ax^{2} + C) \sqrt{ax^{2} + c}} \]
-
関数 \[ \frac{1}{\sqrt{a^{2} - b^{2}}} \arccos \left(\frac{a\cos x + b}{a + b\cos x}\right),\quad \frac{2}{\sqrt{a^{2} - b^{2}}} \arctan \left\{\sqrt{\frac{a - b}{a + b }} \tan \dfrac{1}{2}x\right\} \] はどちらも \(\dfrac{1}{a + b\cos x}\) を導関数に持つ。
-
\(X = a + b\cos x + c\sin x\) で \[ y = \frac{1}{\sqrt{a^{2} - b^{2} -c^{2}}} \arccos \frac{aX - a^{2} + b^{2} + c^{2}}{X \sqrt{b^{2} + c^{2}}} \] なら \(\dfrac{dy}{dx} = \dfrac{1}{X}\) が成り立つ。
-
\(F[f\{\phi(x)\}]\) の導関数が \(F'[f\{\phi(x)\}]\, f'\{\phi(x)\}\phi'(x)\) だと示せ。この結果をさらに複雑なケースに拡張せよ。
-
\(u\) と \(v\) が \(x\) の関数なら次の等式が成り立つ: \[ D_{x} \arctan\frac{u}{v} = \frac{vD_{x}u - uD_{x}v}{u^{2} + v^{2}} \]
-
\(y = (\tan x + \sec x)^{m}\) の導関数は \(my\sec x\) である。
-
\(y = \cos x + i\sin x\) の導関数は \(iy\) である。
-
\(x\cos x\) と \((\sin x)/x\) を微分せよ。曲線 \(y = x\cos x\) と \(y = (\sin x)/x\) の接線が \(x\) 軸と平行になる \(x\) はそれぞれ \(\cot x = x\) と \(\tan x = x\) の根だと示せ。
-
実数 \(a\) が \(a \geq 1\) を満たすなら、方程式 \(\sin x = ax\) は \(x = 0\) 以外の解を持たない。また \(a \lt 1\) なら有限個の根が存在し、その数は \(a\) が \(0\) に近づくにつれて増える (例 17.5)。方程式 \(\tan x = x\) の正の根を \(\xi\) とすると、\(\sin x = ax\) の根の個数が変化する \(a\) は \(\cos\xi\) と表せることを示せ。 [ \(y = ax\) と \(y = \sin x\) が接するような \(a\) の値を求めればよい]
-
\(x \neq 0\) のとき \(\phi(x) = x^{2}\sin(1/x)\) で \(\phi(0) = 0\) なら、\(x \neq 0\) で \[ \phi'(x) = 2x\sin\frac{1}{x} - \cos\frac{1}{x} \] および \(\phi'(0) = 0\) となる。\(\phi'(x)\) は \(x = 0\) で不連続である (§111 の \(\text{(2)}\) を参照)。
-
円 \(x^{2} + y^{2} = a^{2}\) 上の点 \((x_{0}, y_{0})\) における接線と法線の方程式を求めよ。
[ \(y = \sqrt{a^{2} - x^{2}}\) より \(dy/dx = -x/\sqrt{a^{2} - x^{2}}\) だから、接線は \[ y - y_{0} = (x - x_{0}) \left\{-x_{0}/\sqrt{a^{2} - x_{0}^{2}}\right\} \] となる。これは \(xx_{0} + yy_{0} = a^{2}\) と簡略化できる。法線は \(xy_{0} - yx_{0} = 0\) であり、これはもちろん原点を通る]
-
楕円 \((x/a)^{2} + (y/b)^{2} = 1\) および放物線 \((x/a)^{2} - (y/b)^{2} = 1\) 上の任意の点における接線と法線の方程式をそれぞれ求めよ。
-
\(x = \phi(t)\) と \(y = \psi(t)\) で表される曲線のパラメータの値が \(t\) である点における接線と法線は次の方程式で表される: \[ \begin{gathered} \frac{x - \phi(t)}{\phi'(t)} = \frac{y - \psi(t)}{\psi'(t)},\\ \{x - \phi(t)\} \phi'(t) + \{y - \psi(t)\} \psi'(t) = 0 \end{gathered} \]
§120 微分の反復
\(\phi(x)\) から \(\phi'(x)\) を構成したのと同様に \(\phi'(x)\) からは \(\phi''(x)\) を構成できる。この関数 \(\phi''(x)\) を \(\phi(x)\) の 二次導関数 (second derivative) あるいは 二次微分係数 (second differential coefficient) と呼ぶ。\(y = \phi(x)\) の二次導関数は次ようにも表記する: \[ D_{x}^{2}y,\quad \left(\frac{d}{dx}\right)^{2}y,\quad \frac{d^{2}y}{dx^{2}} \]
全く同じ方法で \(\bm{n}\) 次導関数あるいは \(\bm{n}\) 次微分係数を定義できる。これは \[ \phi^{(n)}(x),\quad D_{x}^{n}y,\quad \left(\frac{d}{dx}\right)^{n}y,\quad \frac{d^{n}y}{dx^{n}} \] と表記する。ただし \(n\) 次微分係数が一般的に書ける関数は多くない。そのうちいくつかを次の例で紹介する。
-
\(\phi(x) = x^{m}\) なら次が成り立つ: \[ \phi^{(n)}(x) = m(m - 1) \cdots (m - n + 1)x^{m-n} \] この結果を使えば任意の多項式の \(n\) 次導関数を求められる。
-
\(\phi(x) = (ax + b)^{m}\) なら次が成り立つ: \[ \phi^{(n)}(x) = m(m - 1) \cdots (m - n + 1)a^{n}(ax + b)^{m-n} \] この二つの命題で \(m\) は任意の有理数を表す。もし \(m\) が整数なら \(n \gt m\) で \(\phi^{(n)}(x) = 0\) となる。
-
等式 \[ \left(\frac{d}{dx}\right)^{n} \frac{A}{(x - \alpha)^{p}} = (-1)^{n} \frac{p(p + 1) \cdots (p + n - 1)A}{(x - \alpha)^{p+n}} \] を使えば、任意の有理関数の \(n\) 次導関数を部分分数の和を使った標準形で書ける。
-
\(\dfrac{1}{1-x^{2}}\) の \(n\) 次導関数が \[ \dfrac{1}{2}(n!) \{(1 - x)^{-n-1} + (-1)^{n}(1 + x)^{-n-1}\} \] だと示せ。
-
ライプニッツの定理: \(y\) が積 \(uv\) として表され、\(u\) と \(v\) の最初の \(n\) 個の導関数が得られているとする。このときライプニッツの定理から \(y\) の \(n\) 次導関数が \[ (uv)_{n} = u_{n}v + \binom{n}{1}u_{n-1}v_{1} + \binom{n}{2}u_{n-2}v_{2} + \cdots + \binom{n}{r}u_{n-r}v_{r} + \cdots + uv_{n} \] だと分かる。ここで添え字は微分を表し、例えば \(u_{n}\) は \(u\) の \(n\) 次導関数を表す。定理の証明には \[ \begin{aligned} (uv)_{1} & = u_{1}v + uv_{1},\\ (uv)_{2} & = u_{2}v + 2u_{1}v_{1} + uv_{2},\ \ldots \end{aligned} \] を利用する。こういった関係を繰り返し使えば \[ (uv)_{n} = u_{n}v + a_{n, 1} u_{n-1} v_{1} + a_{n, 2} u_{n-2} v_{2} + \cdots + a_{n, r} u_{n-r} v_{r} + \cdots + uv_{n} \] という形の結論が得られると分かる。
\(r = 1,\ 2,\ \ldots,\ n - 1\) で \(a_{n, r} = \dbinom{n}{r}\) だと仮定し、その上で \(r = 1,\ 2,\ \ldots\ n\) に対して \(a_{n+1, r} = \dbinom{n + 1}{r}\) だと示せばよい。すると数学的帰納法によって全ての \(n\) と \(r\) で \(a_{n, r} = \dbinom{n}{r}\) だと分かる。
\((uv)_{n}\) を微分したときの \((uv)_{n+1}\) の形に注目すると \(u_{n+1-r}v_{r}\) の係数が \[ a_{n, r} + a_{n, r-1} = \binom{n}{r} + \binom{n}{r - 1} = \binom{n + 1}{r} \] になると分かり、証明が完了する。
-
\(x^{m}f(x)\) の \(n\) 次導関数は \[ \begin{gathered} \frac{m!}{(m - n)!} x^{m-n} f(x) + n \frac{m!}{(m - n + 1)!} x^{m-n+1} f'(x) \\ \qquad + \frac{n(n - 1)}{1·2}\, \frac{m!}{(m - n + 2)!} x^{m-n+2} f''(x) + \cdots \end{gathered} \] である。級数は第 \(n + 1\) 項に達するか \(0\) になるまで続く。
-
\(D_{x}^{n}\cos x = \cos(x + \frac{1}{2}n\pi),\ D_{x}^{n}\sin x = \sin(x + \frac{1}{2}n\pi)\) を示せ。
-
\(y = A\cos mx + B\sin mx\) なら \(D_{x}^{2} y + m^{2} y = 0\) が成り立つ。さらに \[ y = A\cos mx + B\sin mx + P_{n}(x) \] で \(P_{n}(x)\) が \(n\) 次の多項式なら \(D_{x}^{n+3} y + m^{2} D_{x}^{n+1} y = 0\) が成り立つ。
-
\(x^{2} D_{x}^{2}y + x D_{x} y + y = 0\) なら \[ x^{2} D_{x}^{n+2} y + (2n + 1)x D_{x}^{n+1} y + (n^{2} + 1) D_{x}^{n} y = 0 \] が成り立つ。
[ライプニッツの定理を使って \(n\) 回微分する]
-
\(\dfrac{Lx + M}{x^{2} - 2Bx + C}\) の \(n\) 次導関数を \(U_{n}\) とすると \[ \frac{x^{2} - 2Bx + C}{(n + 1)(n + 2)} U_{n+2} + \frac{2(x - B)}{n + 1} U_{n+1} + U_{n} = 0 \] が成り立つ。
(Math. Trip. 1900.)
[まず \(n = 0\) の場合の等式を示し、それからライプニッツの定理を使って \(n\) 回微分する]
-
\(\bm{\dfrac{a}{a^{2} + x^{2}} }\) と \(\bm{\dfrac{x}{a^{2} + x^{2}} }\) の \(\bm{n}\) 次導関数: 等式 \[ \frac{a}{a^{2} + x^{2}} = \frac{1}{2i} \left(\frac{1}{x - ai} - \frac{1}{x + ai}\right), \quad \frac{x}{a^{2} + x^{2}} = \frac{1}{2} \left(\frac{1}{x - ai} + \frac{1}{x + ai}\right) \] から \[ D_{x}^{n} \left(\frac{a}{a^{2} + x^{2}}\right) = \frac{(-1)^{n} n!}{2i} \left\{ \frac{1}{(x - ai)^{n+1}} - \frac{1}{(x + ai)^{n+1}} \right\} \] が分かる。\(D_{x}^{n}\{x/(a^{2} + x^{2})\}\) に対しても同様の等式が成り立つ。\(\rho = \sqrt{x^{2} + a^{2}}\) として、サインとコサインが \(x/\rho\) と \(a/\rho\) になる絶対値が最小の実数を \(\theta\) とすれば、\(x + ai = \rho\operatorname{Cis}\theta\) および \(x - ai = \rho\operatorname{Cis}(-\theta )\) となる。ここから \[ \begin{aligned} D_{x}^{n} \frac{a}{a^{2} + x^{2}} & = \frac{(-1)^{n} n!\,\rho^{-n-1}}{2i} [\operatorname{Cis} \{(n + 1)\theta\} - \operatorname{Cis} \{-(n + 1)\theta\}]\\ & = (-1)^{n} n!\, (x^{2} + a^{2})^{-(n+1)/2} \sin \{(n + 1) \arctan \frac{a}{x}\} \end{aligned} \] が分かる。同様に \[ D_{x}^{n} \frac{x}{a^{2} + x^{2}} = (-1)^{n} n!\, (x^{2} + a^{2})^{-(n+1)/2} \cos \{(n + 1) \arctan \frac{a}{x}\} \] が成り立つ。
-
次を示せ: \[ \begin{aligned} D_{x}^{n} \frac{\cos x}{x} & = \frac{1}{x^{n+1}} \{P_{n} \cos(x + \dfrac{1}{2}n\pi) + Q_{n} \sin(x + \dfrac{1}{2}n\pi)\},\\ D_{x}^{n} \frac{\sin x}{x} & = \frac{1}{x^{n+1}} \{P_{n} \sin(x + \dfrac{1}{2}n\pi) - Q_{n} \cos(x + \dfrac{1}{2}n\pi)\} \end{aligned} \] \(P_{n}\) と \(Q_{n}\) はそれぞれ \(n\) 次および \(n - 1\) 次の \(x\) の多項式とする。
-
次を示せ: \[ \begin{gathered} \frac{dx}{dy} = 1 \bigg/\biggl(\frac{dy}{dx}\biggr),\quad \frac{d^{2} x}{dy^{2}} = -\frac{d^{2} y}{dx^{2}} \bigg/ \biggl(\frac{dy}{dx}\biggr)^{3},\\ \frac{d^{3} x}{dy^{3}} = -\biggl\{\frac{d^{3} y}{dx^{3}}\, \frac{dy}{dx} - 3\biggl(\frac{d^{2} y}{dx^{2}}\biggr)\biggr\} \bigg/ \biggl(\frac{dy}{dx}\biggr)^{5} \end{gathered} \]
-
\(yz = 1\) で \(y_{r} = \dfrac{D_{x}^{r}y}{r!},\ z_{s} = \dfrac{D_{x}^{s}z}{s!}\) なら \[ \frac{1}{z^{3}} \begin{vmatrix} z & z_{1}& z_{2}\\ z_{1}& z_{2}& z_{3}\\ z_{2}& z_{3}& z_{4} \end{vmatrix} = \frac{1}{y^{2}} \begin{vmatrix} y_{2}& y_{3}\\ y_{3}& y_{4} \end{vmatrix} \] が成り立つ。
(Math. Trip. 1905.)
-
ダッシュが \(x\) に関する微分を表すとして、 \[ W(y, z, u) = \begin{vmatrix} y & z & u\\ y' & z' & u'\\ y''& z''& u'' \end{vmatrix} \] とすると \[ W(y, z, u) = y^{3}\, W\left(1, \frac{z}{y}, \frac{u}{y}\right) \] が成り立つ。
-
もし \[ ax^{2} + 2hxy + by^{2} + 2gx + 2fy + c = 0 \] なら \[ \frac{dy}{dx} = -\frac{ax + hy + g}{hx + by + f} \] および \[ \frac{d^{2}y}{dx^{2}} = \frac{abc + 2fgh - af^{2} - bg^{2} - ch^{2}}{(hx + by + f)^{3}} \] が成り立つ。
§121 微分に関する諸定理 (ロルの定理)
この節では \(x\) の関数 \(\phi(x)\) の導関数 \(\phi'(x)\) が考えている全ての \(x\) で値を持つとする。もちろんこの仮定により \(\phi(x)\) は連続となる。
\(\phi'(x_{0}) \gt 0\) とする。このとき \(x_{0}\) より小さく \(x_{0}\) に十分近い全ての \(x\) で \(\phi(x) \lt \phi(x_{0})\) が成り立ち、\(x_{0}\) より大きく \(x_{0}\) に十分近い全ての \(x\) で \(\phi(x) \gt \phi(x_{0})\) が成り立つ。
仮定から \(\{\phi(x_{0} + h) - \phi(x_{0})\}/h\) は \(h \to 0\) のとき正の極限 \(\phi'(x_{0})\) に収束する。これは絶対値が十分小さい \(h\) に対して \(\phi(x_{0} + h) - \phi(x_{0})\) と \(h\) が同じ符号を持つときにしか成り立たないが、定理はまさにこのことを示している。この結果は幾何学的に考えても納得できる: \(\phi'(x) \gt 0\) は曲線 \(y = \phi(x)\) の接線が \(x\) 軸と正の角度をなすことを意味する。\(\phi'(x) \lt 0\) の場合の定理を自分で定式化してみるとよい。
定理 A からロルの定理 (Rolle's Theorem) として知られる次の重要な定理が得られる。この定理は非常に大切なので、その前提条件をここに繰り返しておいた方がいいだろう: 導関数 \(\phi'(x)\) が考えている全ての \(x\) で存在するときに限ってロルの定理は正しい。
\(\phi(a) = 0\) かつ \(\phi(b) = 0\) なら、\(a\) と \(b\) の間のとある \(x\) で \(\phi'(x) = 0\) となる。
可能性が二つある。一つは \(\phi(x)\) が \([a, b]\) の全てで \(0\) に等しい場合で、この場合は \(\phi'(x)\) も \([a, b]\) の全てで \(0\) に等しい。一方で考えている区間で \(\phi(x)\) が常に \(0\) に等しくないなら、\(\phi(x)\) が正または負となる \(x\) が存在する。例えば \(\phi(x)\) がどこかで正になるとすれば、§102 の定理 2 から \(a\) でも \(b\) でもない \(\xi\) が存在し、全ての \(\phi(x)\) が \(\phi(\xi)\) 以下となる。このとき \(\phi'(\xi) = 0\) である。もし \(\phi'(x)\) が正だとすると、定理 A から \(x\) より大きく \(\xi\) に十分近い全ての \(x\) で \(\phi(x)\) が \(\phi(\xi)\) より大きくなり、\(\phi(\xi)\) より大きい \(\phi(x)\) が存在することになってしまう。\(\phi'(\xi)\) が負にならないことも同様に示せる。
\(\phi(a) = \phi(b) = k\) なら、\(a\) と \(b\) の間に \(\phi'(x) = 0\) となる \(x\) が存在する。
\(\phi(x) - k = \psi(x)\) とすれば \(\psi(x)\) に定理 B を適用できる。
とある区間全体で \(\phi'(x) \gt 0\) なら、その区間で \(\phi(x)\) は \(x\) の狭義単調増加関数 (§95) である。
考えている区間内の任意の二点を \(x_{1},\ x_{2}\) (\(x_{1} \lt x_{2}\)) とする。\(\phi(x_{1}) \lt \phi(x_{2})\) を示せばよい。まず \(\phi(x_{1})\) は \(\phi(x_{2})\) と等しくない: もし等しいなら定理 B より \(x_{1}\) と \(x_{2}\) の間に \(\phi'(x) = 0\) となる \(x\) が存在するが、これは仮定に反する。同様に \(\phi(x_{1})\) は \(\phi(x_{2})\) 以下である: もしそうでないなら \(\phi'(x_{1})\) が正なことから、定理 A より \(x_{1}\) より大きく \(x_{1}\) に十分近い \(x\) で \(\phi(x)\) は \(\phi(x_{1})\) よりも大きくなる。すると \(x_{1}\) と \(x_{2}\) の間に \(\phi(x_{3}) = \phi(x_{1})\) となる \(x_{3}\) が存在するので、定理 B から \(x_{1}\) と \(x_{3}\) の間に \(\phi'(x) = 0\) となる \(x\) が存在してしまう。
系 2 の結論は、区間 \([a, b]\) の中に例外的な \(x\) 、つまり \(\phi'(x)\) が存在しないか正でない \(x\) が有限個存在したとしても、\(\phi(x)\) がそういった \(x\) で連続な限り正しい。
例外的な \(x\) が一つだけ存在し、それが区間の端 \(a\) に対応する場合を考えれば十分である。\(a \lt x_{1} \lt x_{2} \lt b\) とすると、\(a + \delta \lt x_{1}\) かつ \([a + \delta, b]\) で \(\phi'(x) \gt 0\) が成り立つよう \(\delta\) を選ぶことができ、このとき系 2 より \([a + \delta, b]\) で \(\phi(x_{1}) \lt \phi(x_{2})\) が分かる。後は \(\phi(a) \lt \phi(x_{1})\) を示せば証明が完了する。\(x_{1}\) が \(a\) に向かって減少するとき \(\phi(x_{1})\) は狭義単調減少する。よって \[ \phi(a) = \phi(a + 0) = \lim_{x_{1}\to a+0} \phi(x_{1}) \lt \phi(x_{1}) \] が分かる。
\(\phi(a) \geq 0\) および区間 \([a, b]\) 全体で \(\phi'(x) \gt 0\) なら、\(\phi(x)\) は \([a, b]\) 全体で正となる。
定理 A と系 2 は注意深く比較する価値がある。定理 A と同様に単一の点 \(x = x_{0}\) で \(\phi'(x)\) が正として、\(x\) に十分近い \(x_{1},\ x_{2}\) (\(x_{1} \lt x_{0} \lt x_{2}\)) を取る。すると定理 A から \(\phi(x_{1}) \lt \phi(x_{0})\) および \(\phi(x_{2}) \gt \phi(x_{0})\)、つまり \(\phi(x_{1}) \lt \phi(x_{2})\) が分かる。一方でこれは、\(\phi(x)\) が狭義単調増加になる \(x_{0}\) を含んだ区間が存在することを意味しない。\(x_{1}\) と \(x_{2}\) が \(x_{0}\) から見て反対側にあることが定理の証明において本質的なためである。この点については具体的な例を交えて §124 でさらに議論する。
§122 極大値と極小値 (その 1)
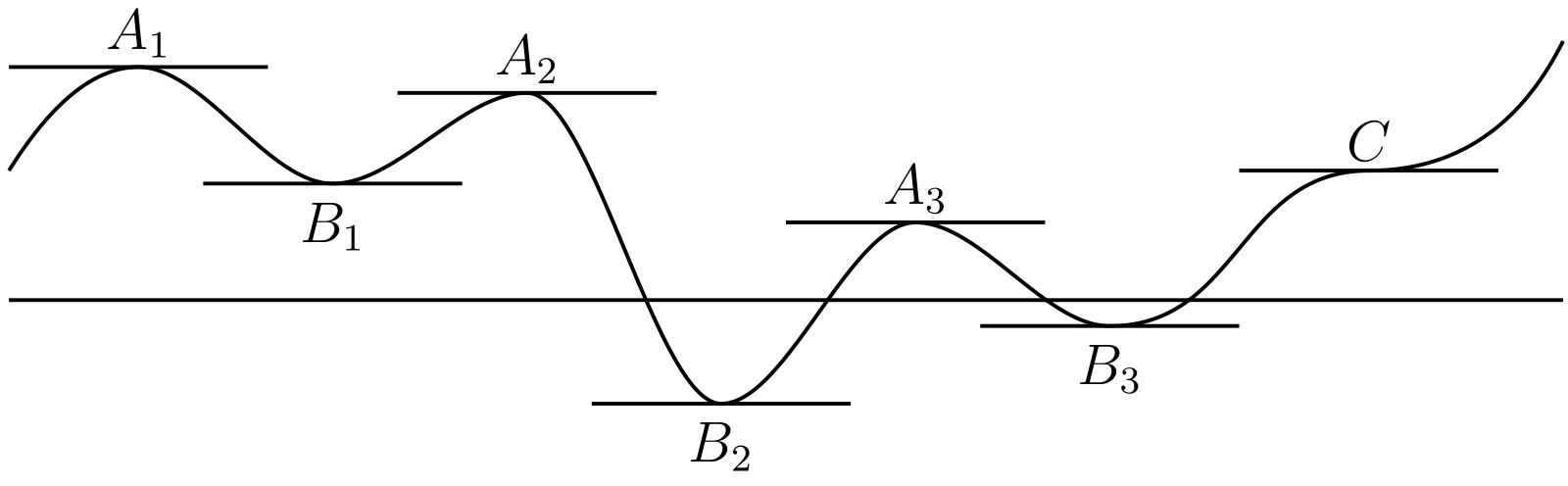
\(x = \xi\) における \(\phi(x)\) の値 \(\phi(\xi)\) が極大 (maximum) であるとは、\(x = \xi\) の近傍における任意の \(\phi(x)\) よりも \(\phi(\xi)\) の方が大きい、つまり \(\xi - \delta \lt x \lt \xi\) および \(\xi \lt x \lt \xi + \delta\) で \(\phi(\xi) \gt \phi(x)\) となる \(x\) の区間 \([\xi - \delta, \xi + \delta]\) が存在することを言う。同様に極小 (minimum) も定義する。例えば 図 39 ではグラフで表される関数が極大の点に \(A\) が対応し、極小の点に \(B\) が対応する。\(A_{3}\) が極大で \(B_{1}\) が極小の状況で \(B_{1}\) における関数の値が \(A_{3}\) における値よりも大きくなっているが、これは何も問題ないことに注意してほしい。
\(x = \xi\) において \(\phi(x)\) が極大または極小となる必要条件は \(\phi'(\xi) = 0\) である3。
これは定理 A から直ちに従う。この条件が十分でないのは 図 39 の点 C を見ればすぐに分かる。あるいは \(y = x^{3}\) なら \(\phi'(x) = 3x^{2}\) であり \(x = 0\) で \(\phi'(x) = 0\) となるが、図 10 のグラフを見れば分かるように \(x^{3}\) は \(x = 0\) で極小でも極大でもない。
しかし「\(\phi'(\xi) = 0\)、かつ \(\xi\) より小さく十分 \(\xi\) に近い全ての \(x\) で \(\phi'(x) \gt 0\)、かつ \(\xi\) より大きく十分 \(\xi\) に近い全ての \(x\) で \(\phi'(x) \lt 0\) 」であれば \(\phi(x)\) は \(x = \xi\) で極大となることは言える。二つの不等式が反対向きなら \(x = \xi\) で極小となる。この仮定が成り立つとき §121 の系 3 より \(\phi(x)\) が \(x\) と共に増加するような区間 \([\xi - \delta, \xi]\) と \(\phi(x)\) が \(x\) と共に減少する区間 \([\xi, \xi + \delta]\) が存在し、これが \(\phi(\xi)\) が極大であることを保証する。
この結果は次のようにも表現できる: \(\phi'(x)\) の符号が \(x = \xi\) で正から負に変化するなら、\(\phi(x)\) は \(x = \xi\) で極大となる。\(\phi'(x)\) の符号が逆方向に変化するなら、\(\phi(x)\) は \(x = \xi\) で極小となる。
§123 極大値と極小値 (その 2)
極大および極小の条件の異なる表現方法があり、こちらが便利になる場合もある。\(\phi(x)\) が二次導関数 \(\phi''(x)\) を持つとする。全ての \(\phi(x)\) に対して \(\phi'(x)\) が存在するわけではないのと同様に、\(\phi'(x)\) が存在するとき \(\phi''(x)\) が必ず存在するわけではない。しかし現在の私たちが扱うことになる関数ではこの条件が満たされることが多い。さてこのとき次が成り立つ:
\(\phi'(\xi) = 0\) かつ \(\phi''(\xi) \neq 0\) なら、\(\phi(x)\) は \(x = \xi\) で極大または極小となる。具体的には \(\phi''(\xi) \lt 0\) なら極大で、\(\phi''(\xi) \gt 0\) なら極小となる。
\(\phi''(\xi) \lt 0\) とする。定理 A から、\(\xi\) より小さく \(\xi\) に十分近い全ての \(x\) で \(\phi'(x)\) が負なこと、そして \(\xi\) より大きく \(\xi\) に十分近い全ての \(x\) で \(\phi'(x)\) が正なことが分かる。つまり \(\phi(x)\) は \(x = \xi\) で極大である。
§124 極大値と極小値 (その 3)
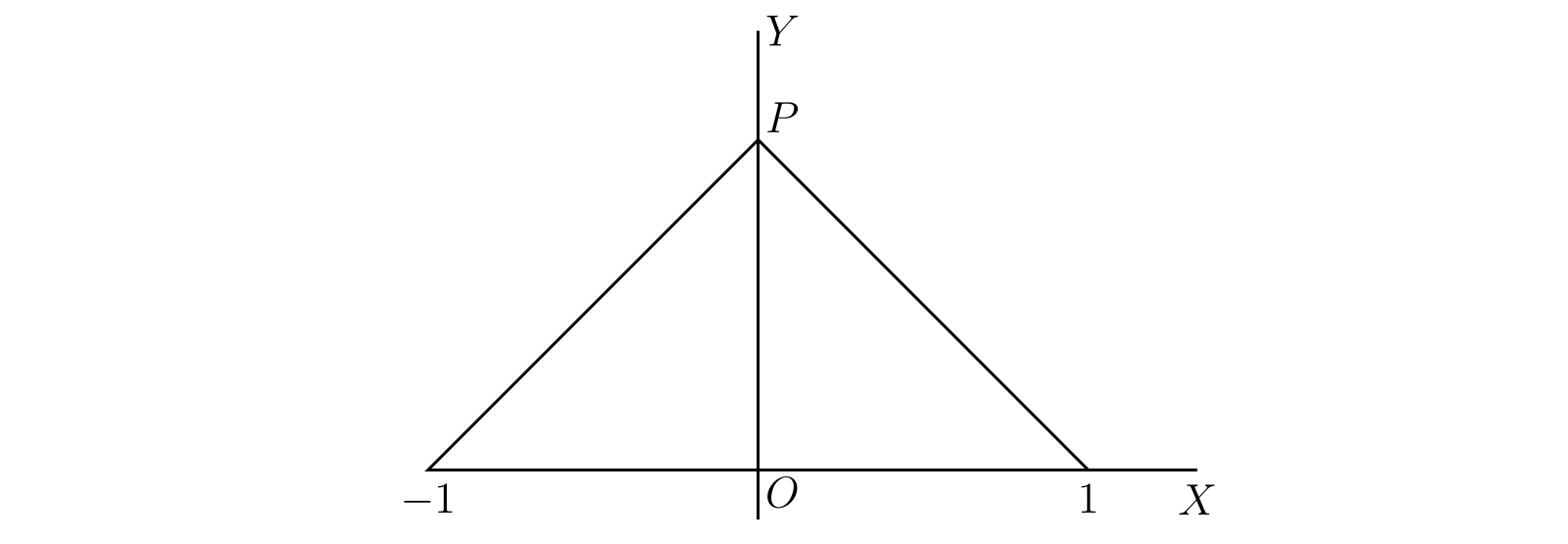
ここまでは (前節を除いて) 考えている区間に含まれる全ての \(x\) で \(\phi(x)\) が導関数を持つ状況を考えてきた。この条件が満たされないなら定理は成り立たない。例えば次の関数は 定理 B の前提を満たすが結論は満たさない: \[ y = 1 - \sqrt{x^{2}} \] ただし平方根は正の値を取るとする。この関数のグラフを 図 40 に示す。この関数は \(\phi(-1) = \phi(1) = 0\) を満たすが、図からも明らかなように \(x\) が負なら \(\phi'(x)\) は \(-1\) で \(x\) が正なら \(\phi'(x)\) は \(1\) である。また \(\phi(x)\) は \(x = 0\) で微分係数を持たず、グラフの点 \(P\) では接線を引けない。つまり \(\phi(x)\) は明らかに \(x = 0\) で極大となるにもかかわらず、\(\phi'(0)\) は存在せず、\(0\) と等しくない。つまり定理 B を使った極大性の判定が失敗する。
仮定したのは導関数 \(\phi'(x)\) の存在だけだが、仮定されていない性質の中に特に重要なものが一つある: それは \(\bm{\phi'(x)}\) が連続関数かどうかである。ここから細かいことだが非常に興味深い疑問が生じる: 関数 \(\phi(x)\) が連続でない導関数を持つことはそもそもあり得るのか? 言い換えると、各点で接線を引けるがその傾きが連続的に変化しないものが存在するか? 常識に照らして考えれば、この疑問に「あり得ない」「存在しない」と答えたくなるかもしれない。しかしその答えが間違っていると示すのは難しくない。
関数 \(\phi(x)\) を \(x \neq 0\) のとき \[ \phi(x) = x^{2}\sin(1/x) \] および \(\phi(0) = 0\) と定義する。このとき \(\phi(x)\) は全ての \(x\) で連続となる。そして \(x \neq 0\) なら \[ \phi'(x) = 2x \sin(1/x) - \cos(1/x) \] であり、そうでないなら \[ \phi'(0) = \lim_{h \to 0} \frac{h^{2}\sin(1/h)}{h} = 0 \] が成り立つ。つまり \(\phi'(x)\) は全ての \(x\) に対して存在するが、\(\phi'(x)\) は \(x = 0\) で不連続となる。\(x \to 0\) のとき \(2x\sin(1/x)\) は \(0\) に向かうが、\(\cos(1/x)\) は下限 \(-1\) と上限 \(1\) の間を振動する。よって \(\phi'(x)\) も \(-1\) と \(1\) の間を振動する。
本質的に同じ例を使うと §121 で予告した例が得られる。\(0 \lt a \lt 1\) に対して、\(x \neq 0\) のとき \[ \phi(x) = x^{2}\sin(1/x) + ax \] および \(\phi(0) = 0\) と定義する。すると \(\phi'(0) = a \gt 0\) なので、定理 A の前提が満たされる。しかし \(x \neq 0\) のとき \[ \phi'(x) = 2x\sin(1/x) - \cos(1/x) + a \] は下限 \(a - 1\) と上限 \(a + 1\) の間を振動する。\(a - 1 \lt 0\) だから、\(\phi'(x) \lt 0\) が成り立つ \(x\) を \(0\) に好きなだけ近くに見つけられる。よって \(x = 0\) を含んだ区間であって \(\phi(x)\) が \(x\) の単調増加関数となるものは存在しない。
ただし一般の導関数 \(\phi'(x)\) が第五章の 例 37.18 で説明した "単純な" 不連続性を持つことはない。つまり \(x \to +0\) のとき \(\phi'(x) \to a\) で \(x \to -0\) のとき \(\phi'(x) \to b\) で \(\phi'(0) = c\) なら必ず \(a = b = c\) であり、\(\phi'(x)\) は \(x = 0\) で連続となる。証明は 例 47.3 で行う。
-
定理 B が \(\phi(x) = (x - a)^{m} (x - b)^{n}\) と \(\phi(x) = (x - a)^{m} (x - b)^{n} (x - c)^{p}\) で正しいことを確認せよ。\(m,\ n,\ p\) は正の整数で \(a \lt b \lt c\) とする。
[最初の関数は \(x = a\) と \(x = b\) で \(0\) となる。そして \[ \phi'(x) = (x - a)^{m-1} (x - b)^{n-1} \{(m + n)x - mb - na\} \] は \(x = (mb + na)/(m + n)\) で \(0\) となるが、この値は \(a\) と \(b\) の間にある。二つ目の関数では二次方程式 \[ (m + n + p)x^{2} - \{m(b + c) + n(c + a) + p(a + b)\}x + mbc + nca + pab = 0 \] が \(a\) と \(b\) および \(b\) と \(c\) の間に根を持つことを示す]
-
次の多項式が \(x \gt 1\) で正だと示せ: \[ 2x^{3} + 3x^{2} - 12x + 7,\quad 3x^{4} + 8x^{3} - 6x^{2} - 24x + 19 \]
-
任意の \(x\) の区間で \(x - \sin x\) が増加関数であること、および \(x\) が \(-\frac{1}{2}\pi\) から \(\frac{1}{2}\pi\) まで増加するとき \(\tan x - x\) が増加することを示せ。\(x\) の関数 \(ax - \sin x\) が単調増加および単調減少となるのは \(a\) がどんな値のときか?
-
\(\tan x - x\) が \(x = \frac{1}{2}\pi\) から \(x = \frac{3}{2}\pi\) や \(x = \frac{3}{2}\pi\) から \(x = \frac{5}{2}\pi\) といった区間でも増加すること、および \(\tan x = x\) の根が各区間にちょうど一つずつ含まれることを示せ (参考: 例 17.4)。
-
問題 3 を使って \(x \gt 0\) で \(\sin x - x \lt 0\) だと示し、ここから \(\cos x - 1 + \frac{1}{2}x^{2} \gt 0\) と \(\sin x - x + \frac{1}{6} x^{3} \gt 0\) を導け。一般に \(x \gt 0\) に対して \[ \begin{aligned} C_{2m} & = \cos x - 1 + \frac{x^{2}}{2!} - \cdots - (-1)^{m} \frac{x^{2m}}{(2m)!},\\ S_{2m+1}& = \sin x - x + \frac{x^{3}}{3!} - \cdots - (-1)^{m} \frac{x^{2m+1}}{(2m+1)!} \end{aligned} \] とすると、\(C_{2m}\) と \(S_{2m + 1}\) は \(m\) が奇数なら正で偶数なら負だと示せ。
-
\(f(x)\) と \(f''(x)\) が連続かつ区間 \([a, b]\) で符号が一定なら、この区間には \(f(x) = 0\) と \(f'(x) = 0\) の根がそれぞれ最大でも一つしか含まれないと示せ。
-
関数 \(u,\ v\) の導関数 \(u',\ v'\) がとある区間で連続で、かつその区間で \(uv' - u'v\) が \(0\) にならないとする。適当な二つの \(u = 0\) の根の間には \(v = 0\) の根があること、およびその逆を示せ。\(u = \cos x,\ \) \(v = \sin x\) としてこの事実を確かめよ。
[二つの \(u = 0\) の根 \(\alpha\) と \(\beta\) の間で \(v\) が \(0\) にならないとする。このとき関数 \(u/v\) は区間 \([\alpha, \beta]\) で連続であり、区間の端で \(0\) となる。よって \((u/v)' = (u'v - uv')/v^{2}\) は \(\alpha\) と \(\beta\) の間のどこかで \(0\) になるが、これは仮定と矛盾する]
-
次の関数が極大および極小となる点を求めよ: \[ \begin{gathered} (x - 1)^{2} (x + 2),\quad x^{3} - 3x,\quad 2x^{3} - 3x^{2} - 36x + 10,\\ 4x^{3} - 18x^{2} + 27x - 7, \quad 3x^{4} - 4x^{3} + 1, \quad x^{5} - 15x^{3} + 3 \end{gathered} \] それぞれの関数のグラフを描け。
[例として最後の関数を考える。この関数の導関数 \(\phi'(x) = 5x^{2} (x^{2} - 9)\) は \(x = -3,\ 0,\ 3\) で \(0\) となる。少し調べれば \(x = -3\) が極大で \(x = 3\) が極小だと分かるが、\(x = 0\) はどちらでもない。\(\phi'(x)\) は \(x = 0\) の両方向で負となる]
-
関数 \((x - a)^{m}(x - b)^{n}\) の極大および極小について議論せよ。\(m\) と \(n\) は正の整数として、\(m\) と \(n\) が奇数および偶数のそれぞれの場合を考えること。さらにこの関数のグラフを描け。
-
前問と同じことを関数 \((x - a) (x - b)^{2} (x - c)^{3}\) について議論せよ。\(a,\ b,\ c\) の大小関係に応じてグラフの形がどう変わるか示せ。
-
\(a,\ b,\ c,\ d\) がどんな値であっても、\((ax + b)/(cx + d)\) が極大または極小となる点を持たないことを示せ。この関数のグラフを描け。
-
次の関数が極大および極小となる点について議論せよ: \[ y = \frac{ax^{2} + 2bx + c}{Ax^{2} + 2Bx + C} \] 分母は複素根を持つとする。
[\(a\) と \(A\) は正だと仮定できる。導関数が \(0\) になるのは \[ (ax + b)(Bx + C) - (Ax + B)(bx + c) = 0 \qquad \text{(1)} \] のときである。この方程式は実根を持つ: 持たないとすると導関数が常に同じ符号を持つことになるが、これは \(y\) が全ての \(x\) で連続で \(x \to +\infty\) および \(x \to -\infty\) のとき \(y \to a/A\) という事実に反する。\(y\) のグラフは直線 \(y = a/A\) とちょうど一回だけ交わるが、\(b/a \gt B/A\) なら十分大きい正の \(x\) ではグラフがこの直線より上にあり、十分大きい負の \(x\) ではグラフがこの直線より下にあること (\(b/a \lt B/A\) ならその逆) が示せる。よって \(b/a \gt B/A\) なら \(\text{(1)}\) の大きい方の根で \(y\) は極大となり、小さい方の根で極小となる。\(b/a \gt B/A\) ならその逆が成り立つ]
-
前問の設定における \(y\) の極大値と極小値は \(ax^{2} + 2bx + c - \lambda(Ax^{2} + 2Bx + C)\) が \(x\) の完全平方式となる \(\lambda\) となる。 [これは \(y = \lambda\) が曲線に接するための条件である]
-
一般に \(R(x) = P(x)/Q(x)\) が極大または極小となる \(x\) の値を \(\lambda\) とすると、\(P(x) - \lambda Q(x) = 0\) は等しい根の組を持つ。
-
\(Ax^{2} + 2Bx + C = 0\) が実根を持つなら、議論は次のようになる。\(\lambda = bA - aB,\ \mu = cA - aC\) とすると \[ y - \frac{a}{A} = \frac{\lambda x + \mu}{A(Ax^{2} + 2Bx + C)} \] が成り立つ。さらに \(\xi = \lambda x + \mu,\ \eta = (A/\lambda^{2})(Ay - a)\) とすれば \[ \eta = \frac{\xi}{(\xi - p)(\xi - q)} \] となる。
この \((x, y)\) から \((\xi, \eta)\) への変形は軸に平行な原点の移動・軸の縮小拡大・座標の反転 (\(\lambda \lt 0\) の場合) からなる。そのため \(x\) の関数 \(y\) の極小値は \(\xi\) の関数 \(\eta\) の極小値に対応する。この逆も成り立ち、極大値についても成り立つ。
\(\xi\) に関する \(\eta\) の導関数は \[ (\xi - p)(\xi - q) - \xi(\xi - p) - \xi(\xi - q) = 0 \] つまり \(\xi^{2} = pq\) のとき \(0\) となる。よって \(\eta\) の導関数は \(p\) と \(q\) の符号が同じなら二つの根を持ち、異なるなら根を持たない。後者の場合の \(\eta\) のグラフを 図 41a に示す。
\(p\) と \(q\) が正ならグラフは 図 41b のようになり、\(\xi = \sqrt{pq}\) で極大となり \(\xi = -\sqrt{pq}\) で極小となる4。
\(p = q\) なら \[ \eta = \frac{\xi}{(\xi - p)^{2}} \] であり、図 41c のようなグラフが得られる。
以上の議論は \(\lambda \neq 0\) を仮定している。\(\lambda = 0\) なら \(a/A = b/B\) であり、 \[ \begin{aligned} y - \frac{a}{A} & = \frac{\mu}{A(Ax^{2} + 2Bx + C)}\\ & = \frac{\mu}{A^{2}(x - x_{1})(x - x_{2})} \end{aligned} \] となる。\(dy/dx = 0\) とすると単一の値 \(x = \frac{1}{2}(x_{1} + x_{2})\) を得る。グラフを描けば、\(\mu\) が正ならこの値で極大となり、負なら極小となることが分かる。\(\mu\) が正の場合のグラフを 図 42 に示す。
[関数 \(y = (ax^{2} + 2bx + c)/(Ax^{2} + 2Bx + C)\) に関する代数的な方法だけを使った完全な一般理論はクリスタル著 Algebra, vol i, pp. 464–7 にある]
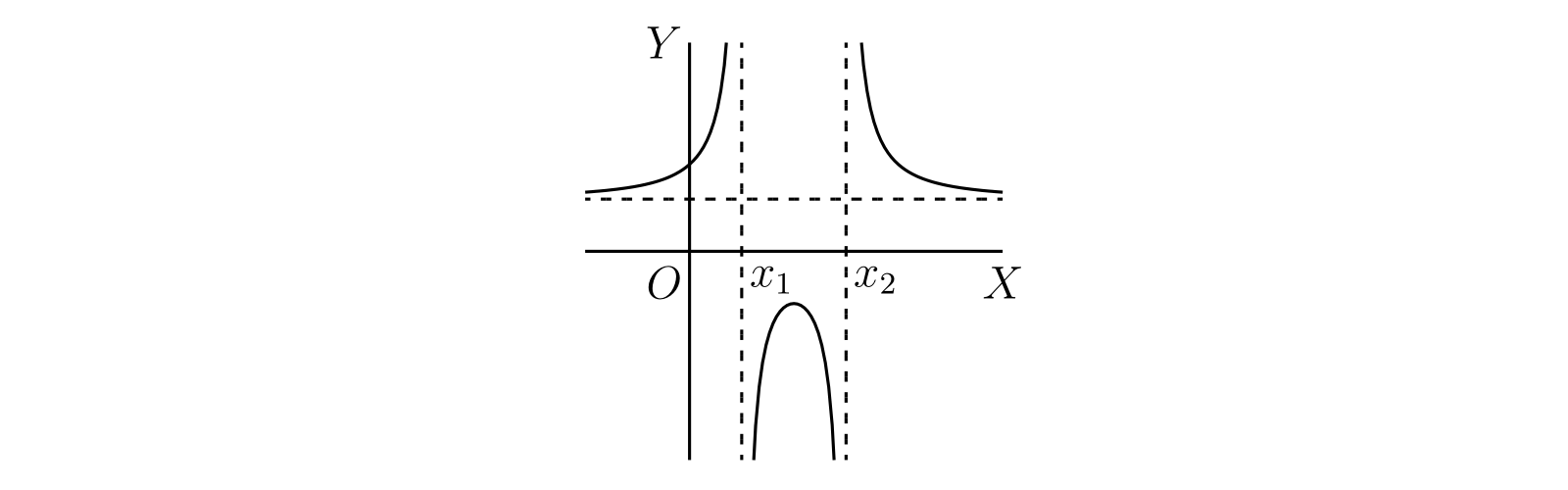 図 42
図 42 -
\(\gamma\) が \(\alpha\) と \(\beta\) の間にあるなら、\(x\) が動くとき \((x - \alpha)(x - \beta)/(x - \gamma)\) は全ての実数の値を取る。そうでないなら、長さ \(4\sqrt{|\alpha - \gamma||\beta - \gamma|}\) の区間を除いた全ての値を取る。
-
\(0 \lt c \lt 1\) なら \[ y = \frac{x^{2} + 2x + c}{x^{2} + 4x + 3c} \] が全ての実数の値を取ることを示し、この場合の関数のグラフを描け
(Math. Trip. 1910.)
-
\((ax^{2} + 2bx + c)/(Ax^{2} + 2Bx + C)\) の形をした関数であって \(x = 1\) と \(x = -1\) でそれぞれ \(2\) と \(3\) の極大値または極小値を取り、\(x = 0\) では \(2.5\) となるものを求めよ。
(Math. Trip. 1908.)
-
\(a\) と \(b\) が正なら、\(\dfrac{(x + a) (x + b)}{(x - a) (x - b)}\) の極大値と極小値は次の値である: \[ -\left(\frac{\sqrt{a} + \sqrt{b}}{\sqrt{a} - \sqrt{b}}\right)^{2},\quad -\left(\frac{\sqrt{a} - \sqrt{b}}{\sqrt{a} + \sqrt{b}}\right)^{2} \]
-
\(\dfrac{(x - 1)^{2}}{(x + 1)^{3}}\) の極大値は \(\dfrac{2}{27}\) である。
-
次の関数の極大値と極小値について議論せよ: \[ \frac{x(x - 1)}{x^{2} + 3x + 3}, \quad \frac{x^{4}}{(x - 1)(x - 3)^{3}},\quad \frac{(x - 1)^{2}(3x^{2} - 2x - 37)}{(x + 5)^{2}(3x^{2} - 14x - 1)} \]
(Math. Trip. 1898.)
[最後の関数を \(P(x)/Q(x)\) と表記すれば \[ P'Q - PQ' = 72(x - 7)(x - 3)(x - 1)(x + 1)(x + 2)(x + 5) \] が成り立つ]
-
\(a\cos x + b\sin x\) が極大および極小となる \(x\) の値を求めよ。関数を \(A\cos(x - B)\) の形に変形することでその結果の正しさを確かめよ。
-
次の関数が極大および極小となる \(x\) の値を求めよ: \[ a^{2}\cos^{2} x + b^{2}\sin^{2} x,\quad A\cos^{2}x + 2H\cos x\sin x + B\sin^{2} x \]
-
\(\dfrac{\sin(x + a)}{\sin(x + b)}\) が極大値および極小値を持たないと示し、この関数のグラフを描け。
-
関数 \[ \frac{\sin^{2}x}{\sin(x + a)\sin(x + b)}\quad (0 \lt a \lt b \lt \pi) \] が極小値 \(0\) と極大値 \[ -\frac{4\sin a\sin b}{\sin^{2}(a - b)} \] を無限に持つと示せ。
(Math. Trip. 1909.)
-
\(a^{2}\sec^{2}x + b^{2}\cosec^{2}x\) の最小値は \((a + b)^{2}\) である。
-
\(\tan 3x \cot 2x\) が \(\dfrac{1}{9}\) と \(\dfrac{3}{2}\) の間の値を取らないことを示せ。
-
直角三角形の斜辺ともう一つの辺の長さの和が固定されたとき、三角形の面積はその二つの辺の間の角度が \(60°\) のとき最大になると示せ。
(Math. Trip. 1909)
-
固定点 \((a, b)\) を通る直線が \(OX\) と \(OY\) に交わる点をそれぞれ \(P\) と \(Q\) とする。\(PQ,\ OP + OQ,\ OP·OQ\) の最小値がそれぞれ \((a^{2/3} + b^{2/3})^{3/2},\ (\sqrt{a} + \sqrt{b})^{2},\ 4ab\) だと示せ。
-
楕円の接線が \(x,\ y\) 軸と交わる点を \(P,\ Q\) とする。\(PQ\) の最小値が短半径と長半径の積に等しいと示せ。
-
円錐曲線 \[ ax^{2} + 2hxy + by^{2} = 1 \] の軸の長さと方向を求めよ。
[\(x\) 軸との角度が \(\theta\) で長さが \(r\) の半径を持つ円錐曲線は \[ \frac{1}{r^{2}} = a\cos^{2} \theta + 2h\cos\theta \sin\theta + b\sin^{2} \theta \] で与えられる。\(r\) が極大および極小となる条件は \(\tan 2\theta = 2h/(a - b)\) である。二つの方程式から \(\theta\) を消去すれば \[ \left(a - \frac{1}{r^{2}}\right) \left(b - \frac{1}{r^{2}}\right) = h^{2} \] を得る]
-
\(x\) と \(y\) が正で \(x + y = k\) なら、\(x^{m}y^{n}\) の最大値は \[ \frac{m^{m} n^{n} k^{m+n}}{(m + n)^{m+n}} \] である。
-
\(x\) が \(y\) が正で \(x^{2} + xy + y^{2} = 3\kappa^{2}\) を満たすとき、\(ax + by\) の最大値は \[ 2\kappa \sqrt{a^{2} - ab + b^{2}} \] である。
[\(ax + by\) が極大なら \(a + b(dy/dx) = 0\) が成り立つ。\(x\) と \(y\) の関係からは \((2x + y) + (x + 2y)(dy/dx) = 0\) が分かる。二つの \(dy/dx\) を等号で結べばよい]
-
\(a,\ b,\ c\) を正の実数とする。\(\theta\) と \(\phi\) が鋭角で \(a \sec\theta + b \sec\phi = c\) が成り立つなら、\(a\cos\theta + b\cos\phi\) は \(\theta = \phi\) のとき極小となる。
§125 平均値の定理 (その 1)
続いて一般的な定理をもう一つ証明する。これはとてつもなく重要な定理であり、平均値の定理 (Mean Value Theorem, Theorem of the Mean) と呼ばれることが多い。
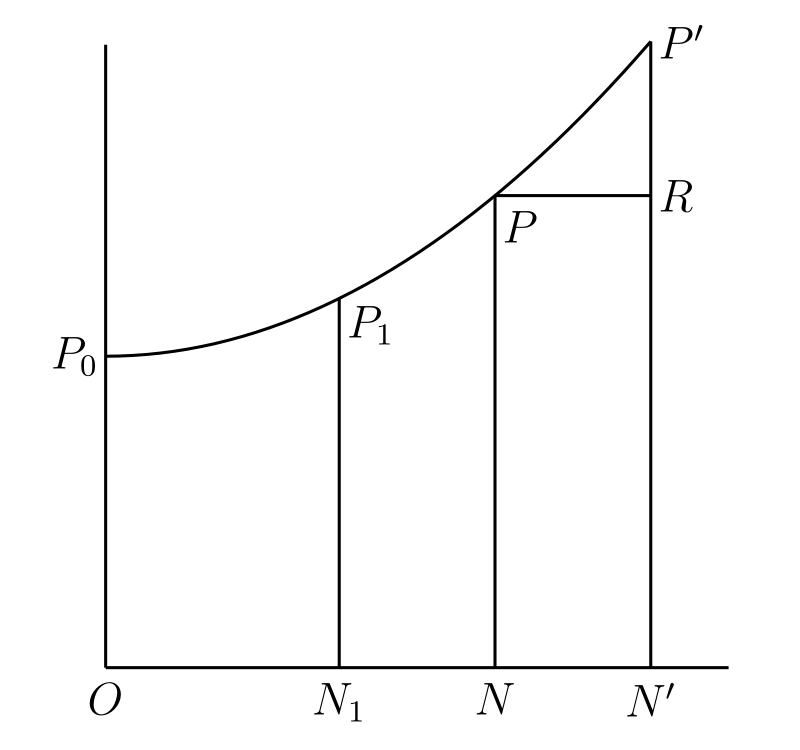
区間 \([a, b]\) 内の全ての \(x\) に対して \(\phi(x)\) が微分係数を持つとする。このとき \(a\) と \(b\) の間にある \(\xi\) であって \[ \phi(b) - \phi(a) = (b - a)\phi'(\xi) \] を満たすものが存在する。
おそらく微分積分学において最も重要なこの定理の厳密な証明を示す前に、その簡単な幾何学的意味を確認しておく。この定理は単に、図 43 のように曲線 \(APB\) 上の全ての点で接線を引けるとき、接線が \(AB\) と平行になる (\(P\) のような) 点が存在することを意味する。\(\phi'(\xi)\) は \(P\) で引いた接線と \(OX\) がなす角度のタンジェントであり、\(\{\phi(b) - \phi(a)\}/(b - a)\) は \(AB\) と \(OX\) がなす角度のタンジェントを表すためである。
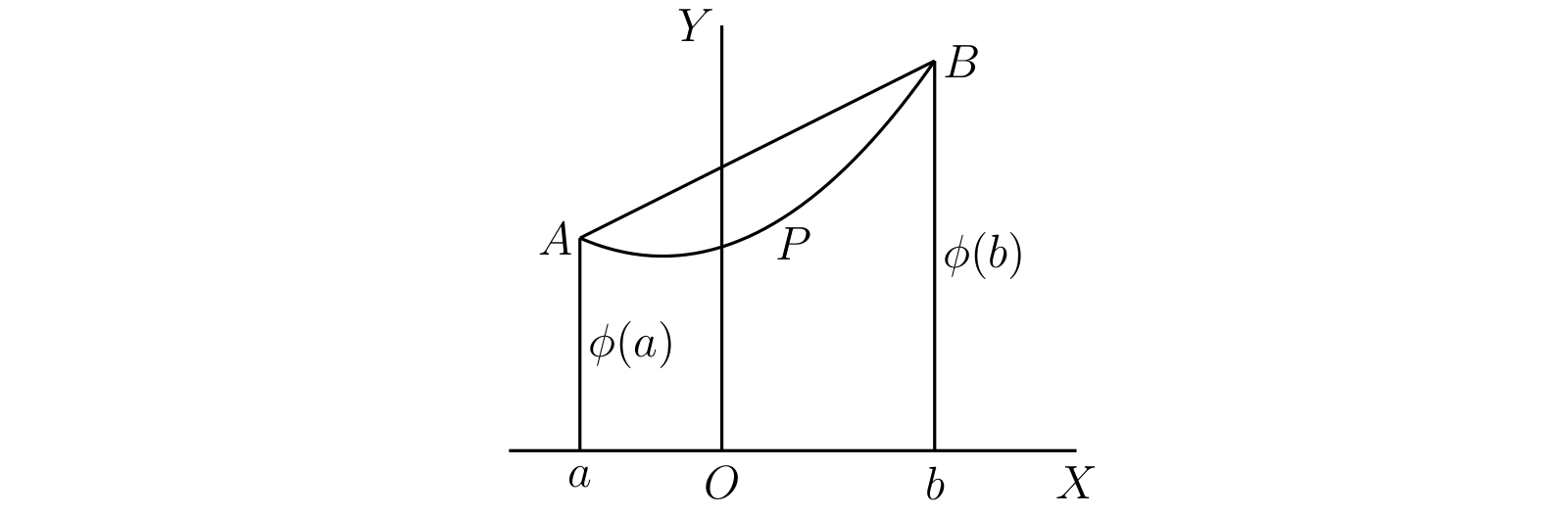
解析的な議論を使った厳密な証明も簡単に行える。関数 \[ \phi(b) - \phi(x) - \frac{b - x}{b - a}\{\phi(b) - \phi(a)\} \] は \(x = a\) と \(x = b\) で \(0\) となる。§121 の定理 B から、この関数の導関数が \(0\) になる \(\xi\) が存在すると分かる。一方で導関数は \[ \frac{\phi(b) - \phi(a)}{b - a} - \phi'(x) \] なので、定理が証明される。この証明では \(\phi'(x)\) の連続性が仮定されていない点に注意してほしい。
平均値の定理を次の形で表すと便利な場合が多い: \[ \phi(b) = \phi(a) + (b - a) \phi'\{a + \theta(b - a)\} \] ここで \(\theta\) は \(0\) と \(1\) の間の実数を表す。もちろん \(a + \theta(b - a)\) というのは「\(a\) と \(b\) の間のとある数 \(\xi\)」を言い換えたに過ぎない。\(b = a + h\) とすれば \[ \phi(a + h) = \phi(a) + h\phi'(a + \theta h) \] を得る。平均値の定理はこの形で表されることが一番多い。
-
式 \[ \phi(b) - \phi(x) - \frac{b - x}{b - a}\{\phi(b) - \phi(a)\} \] が曲線上の点と弦上の点の \(y\) 座標の差を表すことを示せ。
-
\(\phi(x) = x^{2}\) と \(\phi(x) = x^{3}\) で中間値の定理が成り立つことを確認せよ。
[\(\phi(x) = x^{3}\) では、\(a \lt \xi \lt b\) で \((b^{3} - a^{3})/(b - a) = 3\xi^{2}\) だと示す必要がある。つまり \(\frac{1}{3}(b^{2} + ab + a^{2}) = \xi^{2}\) なら \(\xi\) が \(a\) と \(b\) の間にあることを証明する]
-
§124 の最後で説明した定理を平均値の定理を使って示せ。
[\(\phi'(0) = c\) だから、小さい正の \(x\) であって \(\{\phi(x) - \phi(0)\}/x\) が \(c\) にほぼ等しいものを見つけられる。よって平均値の定理から、小さい正の \(\xi\) であって \(\phi'(\xi)\) が \(c\) にほぼ等しいものが存在する。これは \(a = c\) でない限り \(\lim\limits_{x \to +0} \phi'(x) = a\) と矛盾する。同様に \(b = c\) も分かる]
-
平均値の定理を使って §113 の結果 6 を示せ。登場する導関数は全て連続だと仮定してよい。
[\(F\{f(x)\}\) の導関数は定義より \[ \lim \frac{F\{f(x + h)\} - F\{f(x)\}}{h} \] である。中間値の定理から、\(x\) と \(x + h\) の間にある \(\xi\) で \(f(x + h) = f(x) + hf'(\xi)\) が成り立つ。さらに \(f(x)\) と \(f(x) + hf'(\xi)\) の間にある \(\xi_{1}\) で \[ F\{f(x) + hf'(\xi)\} = F\{f(x)\} + hf'(\xi)\, F'(\xi_{1}) \] が成り立つ。\(h \to 0\) のとき \(\xi \to x\) かつ \(\xi_{1} \to f(x)\) だから、\(F\{f(x)\}\) の導関数は \[ \lim f'(\xi)\, F'(\xi_{1}) = f'(x)\, F'\{f(x)\} \] となる]
§126 平均値の定理 (その 2)
中間値の定理からは次の非常に重要な結果が得られる:
とある \(x\) の区間で \(\phi'(x) = 0\) なら、その区間で \(\phi(x)\) は定数である。
\(a\) と \(b\) を区間内の二つの実数とすると \[ \phi(b) - \phi(a) = (b - a) \phi'\{a + \theta(b - a)\} = 0 \] が成り立つためである。簡単な系として、とある区間で \(\phi'(x) = \psi'(x)\) なら関数 \(\phi(x)\) と \(\psi(x)\) の差はその区間内で常に定数となることが分かる。
§127 積分
本章では与えられた関数 \(\phi(x)\) の導関数を求める方法を解説し、最もよく表れる関数をはじめとした様々な \(\phi(x)\) を考えてきた。次はこれと逆の問題、つまり与えられた関数を導関数に持つ関数を求める問題を考えるのが自然である。
与えられた関数を \(\psi(x)\) とする。\(\phi'(x) = \psi(x)\) となる関数 \(\phi(x)\) を求めたい。少し考えれば、この問題が三つの部分からなると分かる:
- 何よりもまず、そのような関数 \(\phi(x)\) が実際に存在するかどうかを知る必要がある。この問題と「関数 \(\phi(x)\) が存在したとして、それを表現する簡単な式を見つける問題」が異なる点に注意しなければならない。
- そのような関数が複数存在するか、つまり問題が唯一の解を持つかどうかを知る必要がある。そして解が複数存在するなら、特定の解を使って全ての解を表すことができるような単純な関係が異なる解の間に存在するかを知る必要がある。
- 解があるなら、その式を見つける方法を知る必要がある。
関数の微分を考えるときに生じる問題と比較すれば、この三つの問題がどんなものであるかがはっきりする。
-
整数 \(m\) に対する \(x^{m}\) や \(\sin x\) のように関数 \(\phi(x)\) が全ての \(x\) に対して微分係数を持つこともある。しかし \(\sqrt[3]{x}\) や \(\tan x\) あるいは \(\sec x\) のように常に導関数を持つわけではない関数もある。さらに導関数が一つも存在しない関数もある: 例 37.20 で考えた関数は全ての点で不連続であり、よって任意の \(x\) で微分係数は存在しない。それから特定の \(x\) の値でのみ微分係数を持たない関数もこの章で考えた。例えば \(\sqrt[3]{x}\) は特別な値 (ここでは \(x = 0\)) で微分係数を持たない連続関数の例となる。導関数を一切持たない連続な関数、つまり接線を引けない連続曲線が存在するのかという疑問も生じるが、これはこの本の範囲を超える。常識的に考えれば「存在しない」が答えだが、§111 でも触れた通り、これは常識が間違っていることを高等数学が証明できる例である。
いずれにせよ「\(\phi(x)\) は導関数 \(\phi'(x)\) を持つか?」という質問の答えが状況によって異なることは確かである。そして逆の質問「導関数が \(\psi(x)\) となる関数 \(\phi(x)\) は存在するか?」にも異なる答えが存在する。答えが「存在しない」の場合は前に見た: \(x\) が \(0\) より小さいとき \(a\)、\(0\) と等しいとき \(b\)、\(0\) より大きいとき \(c\) となる関数を \(\psi(x)\) とすれば、\(a = b = c\) でない限り質問の答えは「存在しない」となる (例 47.3)。
この場合には与えられた関数が不連続となっているが、これからは \(\psi(x)\) が連続と仮定する。すると答えは「存在する」となる: \(\bm{\psi(x)}\) が連続なら、\(\bm{\phi'(x) = \psi(x)}\) となる \(\bm{\phi(x)}\) が存在する。証明は第七章で行う。
-
二つ目の問題は難しくない。微分の場合には定義が直接与えられており、導関数が複数存在しないことはそこから明らかだった。逆の問題もほぼ同じ程度に簡単である。\(\phi(x)\) が問題の解なら、任意の定数 \(C\) に対する \(\phi(x) + C\) も解となり、全ての可能な解は \(\phi(x) + C\) という形に書ける。これは §126 から直ちに従う。
-
実際に \(\phi(x)\) から \(\phi'(x)\) を見つけるという実践的な問題は、関数が簡単な記号の組み合わせである限りそれほど難しくなかった。しかし逆の問題はずっと難しい。何がこの問題を難しくしているかは今後明らかになるだろう。
\(\psi(x)\) を \(\phi(x)\) の導関数とする。このとき \(\phi(x)\) を \(\psi(x)\) の積分 (integral) あるいは積分関数 (integral function) と呼ぶ。そして \(\psi(x)\) から \(\phi(x)\) を得る操作を 積分 (integration) と呼ぶ。
次の表記を使うことにする: \[ \phi(x) = \int \psi(x)\, dx \] 言うまでもないが、\(\int \ldots dx\) は \(d/dx\) と同じくある操作を表す一つの記号としてみなさなければならない。\(d/dx\) の \(d\) や \(dx\) が意味を持たないのと同様に、積分記号の \(\int\) や \(dx\) を切り離しても意味はない。
§128 積分と対数関数
この章の前半部分の結果から、最も頻繁に登場する関数の積分が得られる。例えば \[ \int x^{m}\, dx = \frac{x^{m+1}}{m + 1},\quad \int \cos x\, dx = \sin x,\quad \int \sin x\, dx = -\cos x \qquad \text{(1)} \] である。
この等式は、左辺の積分記号の中にある関数の積分の一つが右辺の関数であると解釈されなければならない。もちろん最も一般的な積分は右辺に定数 \(C\) を加えることで得られる。この定数は積分定数 (arbitrary constant of integration) と呼ばれる。
一つ目の等式には一つだけ例外がある。それは \(m = -1\) の場合で、このとき右辺が意味を持たなくなる。多項式と有理関数の微分が \(1/x\) にならないことは前に見た (例 42.4)。
\(D_{x}F(x) = 1/x\) となる関数 \(F(x)\) が本当に存在することは次章で示すので、ここでは \(F(x)\) が存在するとして話を進める。明らかにこの関数 \(F(x)\) は多項式でもなければ有理関数でもない。実は \(F(x)\) は本質的に新しい関数であり、今まで考えてきたどの関数のクラスにも属さないことが示せる。言い換えると、これまでに出てきた関数を表す記号を有限回組み合わせただけではこの \(F(x)\) を表せない。残念ながらこの証明は込み入っている上にあまり面白くないのでこの本には載せられないが、\(F(x)\) の性質を体系的に調べる第九章ではこの問題をもう少し深く議論する。
\(x\) が正だと仮定する。そして \[ \int \frac{dx}{x} = \log x \qquad \text{(2)} \] と表記し、右辺の関数を対数関数 (logarithmic function) と呼ぶ。まずは正の \(x\) に対してだけ定義する。
次に \(x\) を負とする。すると \(-x\) が正なので、\(\log(-x)\) は上の方法で定義される。また \[ \frac{d}{dx} \log(-x) = \frac{-1}{-x} = \frac{1}{x} \] なので、\(x\) が負なら \[ \int \frac{dx}{x} = \log(-x) \qquad \text{(3)} \] が成り立つ。
\(\text{(2)}\) と \(\text{(3)}\) はまとめて次のように書ける: \[ \int \frac{dx}{x} = \log(±x) = \log|x| \qquad \text{(4)} \] ただし符号は \(±x\) が正になるように取る。この等式は \(x = 0\) を除く全ての \(x\) で成り立つ。
第九章で証明する \(\log x\) の性質の中で最も重要なものは次の式で表される: \[ \log 1 = 0,\quad \log \frac{1}{x} = -\log x,\quad \log xy = \log x + \log y \] 二番目の式は一番目と三番目の式から得られる。これらの等式はこの章の内容に必要ではないが、利用すると式を簡単に表せる場合もある。
三番目の式からは、\(\log x^{2}\) が \(x \gt 0\) なら \(2\log x\) に等しく、\(x \lt 0\) なら \(2 \log (-x)\) に等しいと分かる。まとめて書けば \(2 \log |x|\) であり、\(\text{(4)}\) は次の式と同値となる: \[ \int \frac{dx}{x} = \dfrac{1}{2}\log x^{2} \qquad \text{(5)} \]
\(\text{(1)}\) から \(\text{(3)}\) にある五つの等式は積分学で最も重要な標準形の積分である。ここには次の二つの等式も加えておくべきだろう5: \[ \int \frac{dx}{1 + x^{2}} = \arctan x,\quad \int \frac{x}{\sqrt{1 - x^{2}}} = ±\arcsin x \qquad \text{(6)} \]
§129 多項式の積分
§113 で述べた一般的な定理と同じものは積分に対しても当然存在する。例えば \[ \int \{f(x) + F(x)\}\, dx = \int f(x) dx + \int F(x)\, dx, \qquad \text{(1)} \] \[ \int kf(x)\, dx = k\int f(x)\, dx \qquad \text{(2)} \] はすぐに分かる。
この等式はもちろん積分定数が適切に付いているものとして解釈する。つまり \(\text{(1)}\) は、\(f(x)\) の任意の積分と \(F(x)\) の任意の積分の和が \(f(x) + F(x)\) のとある積分になると主張している。
この定理を使えば、\(\sum A_{\nu} f(\nu)(x)\) という形をした関数、つまり積分が分かっている関数に定数を乗じた項の有限個の和の積分が求められるようになる。特に多項式の積分が求められる: \[ \int (a_{0}x^{n} + a_{1}x^{n-1} + \cdots + a_{n})\, dx = \frac{a_{0}x^{n+1}}{n + 1} + \frac{a_{1}x^{n}}{n} + \cdots + a_{n}x \]
§130 有理関数の積分 (その 1)
多項式の積分の後は有理関数を考えるのが自然である。\(R(x)\) を §117 で示した標準形、つまり多項式 \(\Pi(x)\) と \(A/(x -\alpha)^{p}\) という形の項の和として表された有理関数とする。
多項式の部分および \(p \neq 1\) の項についてはすぐに積分が求まる。なぜなら \[ \int \frac{A}{(x - \alpha)^{p}}\, dx = -\frac{A}{p - 1}\, \frac{1}{(x - \alpha)^{p-1}} \] が実数および複素数の \(\alpha\) に対して成り立つためである (§117)。
\(p = 1\) の項の積分は少し難しくなる。§113 の結果 6 からは \[ \int F'\{f(x)\}\, f'(x)\, dx = F\{f(x)\} \qquad \text{(3)} \] が分かる。\(a,\ b\) を実数として \(f(x) = ax + b\) とおく。\(F(x),\ F'(x)\) を \(\phi(x),\ \psi(x)\) と書けば、\(\psi(x)\) の積分が \(\phi(x)\) となる。そして \[ \int \psi(ax + b)\, dx = \frac{1}{a}\phi(ax + b) \qquad \text{(4)} \] が成り立つ。
よって例えば \[ \int \frac{dx}{ax + b} = \frac{1}{a} \log|ax + b| \] であり、特に実数 \(\alpha\) に対して \[ \int \frac{dx}{x - \alpha} = \log|x - \alpha| \] が成り立つ。これを使えば \(R(x)\) の \(p = 1\) の項のうち \(\alpha\) が実数なものについては積分を計算できる。残されたのは \(p = 1\) かつ \(\alpha\) が複素数である場合である。
これに対処するために、\(R(x)\) の係数が全て実数であるという仮定を追加する。すると \(\alpha = \gamma + \delta i\) が重複度 \(m\) の \(Q(x) = 0\) の根のとき、その共役 \(\bar{\alpha} = \gamma + \delta i\) も重複度 \(m\) の \(Q(x) = 0\) の根となる。よって \(R(x)\) の分解に部分分数 \(A_{p}/(x - \alpha)^{p}\) が表れるなら、\(\bar{A}_{p}/(x - \bar{\alpha})^{p}\) も同じく表れる。ここで \(\bar{A}_{p}\) は \(A_{p}\) の共役を表す。この事実は部分分数を得る代数的な手続きの性質から分かり、この手続きは代数の文献で詳しく説明されている6。
よって \(R(x)\) を部分分数で表したときに \((\lambda + \mu i)/(x - \gamma - \delta i)\) という項が含まれるなら、\((\lambda - \mu i)/(x - \gamma + \delta i)\) という項も含まれる。この二つの項の和は \[ \frac{2\{\lambda(x - \gamma) - \mu\delta\}}{(x - \gamma)^{2} + \delta^{2}} \] である。これを一般的に書けば \[ \frac{Ax + B}{ax^{2} + 2bx + c} \] となり、\(b^{2} \lt ac\) が成り立つ。このとき \(\lambda,\ \mu,\ \gamma,\ \delta\) と \(A,\ B,\ a,\ b,\ c\) の間の関係が \[ \lambda = A/2a,\quad \mu = -D/(2a\sqrt{\Delta}),\quad \gamma = -b/a,\quad \delta = \sqrt{\Delta}/a \] であることは簡単に確認できる。ここで \(\Delta = ac - b^{2}\) および \(D = aB - bA\) とする。
\(\text{(3)}\) で \(F\{f(x)\}\) を \(\log |f(x)|\) とすると \[ \int \frac{f'(x)}{f(x)}\, dx = \log |f(x)| \qquad \text{(5)} \] を得る。さらに \(f(x) = (x - \lambda)^{2} + \mu^{2}\) とすれば \[ \int \frac{2(x - \lambda)}{(x - \lambda)^{2} + \mu^{2}}\, dx = \log\{(x - \lambda)^{2} + \mu^{2}\} \] であり、さらに §128 の等式 \(\text{(6)}\) とこの節の \(\text{(4)}\) からは \[ \int \frac{-2\delta\mu}{(x - \lambda)^{2} + \mu^{2}}\, dx = -2\delta \arctan \left(\frac{x - \lambda}{\mu}\right) \] が分かる。
以上の二つの式を使えば、\(R(x)\) に含まれる二つの \(p = 1\) の項の和を積分できる。よって任意の実係数の有理関数は、その分母の因数が全て求まるなら、積分を求められる。その積分は一つの多項式・複数の \(-\frac{A}{p - 1}\, \frac{1}{(x - \alpha)^{p-1}}\) の形をした有理関数・複数の対数関数・複数のタンジェントの逆関数の和として書ける。
もし \(\alpha\) が複素数なら今示した積分結果の有理関数が \(A\) と \(\alpha\) を共役にしたものと共に生じ、この二つの関数の和が実有理関数となることを最後に付け加えておく。
-
\(\Delta \lt 0\) なら次の等式が成り立つと示せ: \[ \int \frac{Ax + B}{ax^{2} + 2bx + c}\, dx = \frac{A}{2a} \log |X| + \frac{D}{2a \sqrt{-\Delta}} \log \left|\frac{ax + b - \sqrt{-\Delta}}{ax + b + \sqrt{-\Delta}}\right| \] ただし \(X = ax^{2} + bx + c\) とする。さらに \(\Delta \gt 0\) なら \[ \int \frac{Ax + B}{ax^{2} + 2bx + c}\, dx = \frac{A}{2a} \log |X| + \frac{D}{2a \sqrt{\Delta}} \arctan \left(\frac{ax + b}{\sqrt{\Delta}}\right) \] だと示せ。両方において上と同じく \(\Delta = ac - b^{2}\) および \(D = aB - bA\) とする。
-
\(ac = b^{2}\) となる特殊な場合には、この積分は \[ -\frac{D}{a(ax + b)} + \frac{A}{a} \log |ax + b| \] となる。
-
\(Q(x) = 0\) の根が相異なる実数で、\(P(x)\) の次数が \(Q(x)\) より小さいなら \[ \int R(x)\, dx = \sum \frac{P(\alpha)}{Q'(\alpha)} \log |x - \alpha| \] が成り立つと示せ。総和は \(Q(x) = 0\) の根 \(\alpha\) について取る。
[\(\alpha\) に対応する分数の形は、\(x \to \alpha\) で \[ \frac{Q(x)}{x - \alpha} \to Q'(\alpha),\quad (x - \alpha) R(x) \to \frac{P(\alpha)}{Q'(\alpha)} \] となる事実から分かる]
-
\(Q(x)\) の根が全て実数で、\(\alpha\) が唯一の二重根であり、その他は全て単純な根とする。\(P(x)\) の次数が \(Q(x)\) より小さいなら、積分は \(A/(x - \alpha) + A'\log |x - \alpha| + \sum B\log |x - \beta|\) となる。ここで \[ A = -\frac{2P(\alpha)}{Q''(\alpha)},\quad A' = \frac{2\{3P'(\alpha) Q''(\alpha) - P(a) Q'''(\alpha)\}} {3\{Q''(\alpha)\}^{2}},\quad B = \frac{P(\beta)}{Q'(\beta)} \] であり、総和は \(\alpha\) 以外の \(Q(x) = 0\) の根 \(\beta\) について取る。
-
次の積分を計算せよ: \[ \int \frac{dx}{\{(x - 1) (x^{2} + 1)\}^{2}} \]
[部分分数で表すと \[ \frac{1}{4(x - 1)^{2}} - \frac{1}{2(x - 1)} - \frac{i}{8(x - i)^{2}} + \frac{2 - i}{8(x - i)} + \frac{i}{8(x + i)^{2}} + \frac{2 + i}{8(x + i)} \] であり、積分は \[ -\frac{1}{4(x - 1)} - \frac{1}{4(x^{2} + 1)} - \dfrac{1}{2} \log |x - 1| + \dfrac{1}{4} \log (x^{2} + 1) + \dfrac{1}{4} \arctan x \] となる]
-
次の積分を計算せよ: \[ \begin{gathered} \frac{x}{(x - a)(x - b)(x - c)},\quad \frac{x}{(x - a)^{2}(x - b)},\quad \frac{x}{(x - a)^{2} (x - b)^{2}},\quad \frac{x}{(x - a)^{3}},\\ \frac{x}{(x^{2} + a^{2}) (x^{2} + b^{2})},\quad \frac{x^{2}}{(x^{2} + a^{2}) (x^{2} + b)^{2}},\quad \frac{x^{2} - a^{2}}{x^{2}(x^{2} + a^{2})},\quad \frac{x^{2} - a^{2}}{x(x^{2} + a^{2})^{2}} \end{gathered} \]
-
次の等式を示せ: \[ \begin{alignedat}{3} \int \frac{dx}{1 + x^{4}} & = \frac{1}{4\sqrt{2}} \biggl\{ & & \log \biggl(\frac{1 + x\sqrt{2} + x^{2}}{1 - x\sqrt{2} + x^{2}}\biggr) & & + 2\arctan \biggl(\frac{x\sqrt{2}}{1 - x^{2}}\biggr)\biggr\},\\ \int \frac{x^{2}\, dx}{1 + x^{4}} & = \frac{1}{4\sqrt{2}} \biggl\{ & - & \log \biggl(\frac{1 + x\sqrt{2} + x^{2}}{1 - x\sqrt{2} + x^{2}}\biggr) & & + 2\arctan \biggl(\frac{x\sqrt{2}}{1 - x^{2}}\biggr)\biggr\},\\ \int \frac{dx}{1 + x^{2} + x^{4}} & = \frac{1}{4\sqrt{3}}\biggl\{ & \sqrt{3}& \log \biggl(\frac{1 + x + x^{2}}{1 - x + x^{2}}\biggr) & & + 2\arctan \biggl(\frac{x\sqrt{3}}{1 - x^{2}}\biggr)\biggr\} \end{alignedat} \]
§131 有理関数の積分 (その 2)
§130 では任意の実有理関数 \(R(x)\) の積分を計算する一般的な方法を示したが、これは方程式 \(\bm{Q(x) = 0}\) が解けることを前提としていた。単純な場合 (例えば 例 48.5) では方程式を解くのは簡単である。しかし複雑なケースでは方程式を解くのに必要な労力が途方もなく大きくなり、他の方法を使わざるを得なくなる。積分の実践的な問題について詳しく議論するのはこの本の目的ではない。詳細な知識が必要な読者はグルサ著 Cours d'Analyse, second ed., vol. i, pp. 246 et seq. およびバートランド著 Calcul Intégral そしてブロムウィッチ博士による小冊子 Elementary Integrals (Bowes and Bowes, 1911) を参照してほしい。
\(Q(x) = 0\) が代数的に解けない場合には部分分数を使った方法は一般に失敗するので、別の方法が必ず必要になる7。
§132 代数関数の積分
次に考えるのは当然代数関数の積分である。\(x\) の代数関数 \(y\) の積分を求めよう。しかしここでは、一見するともっと一般的な次の積分を考えた方が議論が上手く進む: \[ \int R(x, y)\, dx \] \(R(x, y)\) は \(x\) と \(y\) の有理関数とする。こうして表すとより一般的な問題を扱っているように見えるが、関数 \(R(x, y)\) も \(x\) の代数関数なので (例 14.6)、考えている問題は変わらない。実際に使う形を決めるのは扱いやすさだけである: 例えば \[ \frac{px + q + \sqrt{ax^{2} + 2bx + c}} {px + q - \sqrt{ax^{2} + 2bx + c}} \] という関数は、そのまま \(x\) の代数関数とみなすよりも \(x\) と代数関数 \(\sqrt{ax^{2} + 2bx + c}\) の関数とみなした方がずっと分かりやすい。
§133 置換積分と有理化
§130 の式 \(\text{(3)}\) から、\(\displaystyle \int \psi(x)\, dx = \phi(x)\) のとき次の等式が成り立つと分かる: \[ \int \psi\{f(t)\}\, f'(t)\, dt = \phi\{f(t)\} \qquad \text{(1)} \]
積分がすぐに計算できない \(\psi(x)\) の中には、この等式を使うと積分が行えるものが多くある。この手続きを一般的に言えば「新しい変数 \(t\) の関数 \(f(t)\) を使って \(x = f(t)\) として、\(\psi(x)\) を簡略化する。\(f'(t)\) を乗じた \(\psi\{f(t)\}\, f'(t)\) を積分できるかを確認し、もしできるならその結果を \(x\) の形に書き直す」となる。この手続きで生じる \(t\) の関数 \(\psi\{f(t)\}\, f'(t)\) の積分なら簡単に計算できる場合が多い。例えばこれが有理関数なら必ず積分を計算できるし、そうでなくても積分ができるように \(x\) と \(t\) の間の関係を選ぶことがたいていは可能である。例えば有理関数 \(R(x)\) に対する \(R(\sqrt{x})\) の積分は、\(x = t^{2}\) とすれば \(2tR(t^{2})\) の積分の問題となって \(t\) の有理関数の積分に帰着される。この積分方法は有理化による積分 (integration by ratinalisation) と呼ばれ、非常に広い応用を持つ。
先ほどまで考えていた代数関数の積分問題への応用はすぐに分かる:
\(x\) と \(y\) がどちらも \(t\) の有理関数となるように \(t\) を選べるなら、\(x = R_{1}(t)\) および \(y = R_{2}(t)\) とすれば \[ \int R(x, y)\, dx = \int R\{R_{1}(t), R_{2}(t)\}\, R_{1}'(t)\, dt \] が成り立つ。右辺は \(t\) の有理関数の積分であり、§130 の方法を使えば計算できる。
\(x\) と \(y\) に関連付いた補助変数 \(t\) であってこの条件を満たすものを見つけられるための条件の一般的な議論はこの本の範囲を超える。ここからは単純で興味深い特殊なケースをいくつか考えるだけとする。
§134 円錐曲線で関連付いた変数の積分
\(x\) と \(y\) が次の形をした方程式で関連付いているとする: \[ ax^{2} + 2hxy + by^{2} + 2gx + 2fy + c = 0 \] 言い換えると、\(x\) の関数としての \(y\) のグラフが円錐曲線だとする。\((\xi, \eta)\) をその円錐曲線上の任意の点として、\(x - \xi = X,\ y - \eta = Y\) とおく。\(x\) と \(y\) の間の関係を \(X\) と \(Y\) を使って表すと次の形になる: \[ aX^{2} + 2hXY + bY^{2} + 2GX + 2FY = 0 \] ここで \(F = h\xi + b\eta + f\) および \(G = a\xi + h\eta + g\) である。\(Y = tX\) とすると、\(X\) と \(Y\) の両方を \(t\) の有理関数として表せる。よって \(x\) と \(y\) も同様に \(t\) の有理関数として表すことができ、実際に計算すると \[ x - \xi = -\frac{2 (G + Ft)}{a + 2ht + bt^{2}},\quad y - \eta = -\frac{2t(G + Ft)}{a + 2ht + bt^{2}} \] となる。この関係を使えば前節で説明した有理化の手続きを実行できる。
等式 \[ hx + by + f = -\dfrac{1}{2}(a + 2ht + bt^{2}) \frac{dx}{dt} \] が成り立ち、ここから \[ \int \frac{dx}{hx + by + f}= -2\int \frac{dt}{a + 2ht + bt^{2}} \] となることを確認せよ。積分ではこの事実を利用する。
\(h^{2} \gt ab\) なら次のように議論すると少し楽ができる。このとき円錐曲線は双曲線であり、その漸近線は \[ ax^{2} + 2hxy + by^{2} = 0 \] が表す二つの直線とそれぞれ平行である。そこで \[ b(y - \mu x) (y - \mu' x) = 0 \] とする。さらに \(y - \mu x = t\) とおけば、元の双曲線上の \((x, y)\) について \[ y - \mu x = t,\quad y - \mu' x = -\frac{2gx + 2fy + c}{bt} \] を得る。\(x\) と \(y\) を \(t\) の有理関数として表せるのは明らかである。次節では重要な例への応用を使ってこの処理を説明する。
§135 \(1/\sqrt{ax^{2} + 2bx + c}\) の積分
\(y^{2} = ax^{2} + 2bx + c\) で \(a \gt 0\) とする。\(y + x\sqrt{a} = t\) とおけば \[ 2\frac{dx}{dt} = \frac{(t^{2} + c)\sqrt{a} + 2bt}{(t\sqrt{a} + b)^{2}},\quad 2y = \frac{(t^{2} + c)\sqrt{a} + 2bt}{t\sqrt{a} + b} \] を得る。ここから \[ \int \frac{dx}{y} = \int \frac{dt}{t\sqrt{a} + b} = \frac{1}{\sqrt{a}} \log \left|x\sqrt{a} + y + \frac{b}{\sqrt{a}}\right| \qquad \text{(1)} \] が分かる。具体的に \(a = 1,\ b = 0,\ c = a^{2}\) あるいは \(a = 1,\ b = 0,\ c = -a^{2}\) とすれば \[ \int \frac{dx}{\sqrt{x^{2} + a^{2}}} = \log \{x + \sqrt{x^{2} + a^{2}}\},\quad \int \frac{dx}{\sqrt{x^{2} - a^{2}}} = \log |x + \sqrt{x^{2} - a^{2}}| \qquad \text{(2)} \] を得る。この等式の正しさは実際に右辺を微分してみればすぐに分かる。この二つの等式は次の等式と合わせて考えるとよい: \[ \int \frac{dx}{\sqrt{a^{2} - x^{2}}} = \arcsin\frac{x}{a} \qquad \text{(3)} \] これは最初の一般形で \(a \lt 0\) の場合に対応する。\(\text{(3)}\) では \(a \gt 0\) が仮定されており、\(a \lt 0\) なら \(\arcsin(x/|a|)\) となる (参考: §119)。実際の積分では、一般的な積分の問題を (次節で説明される方法で) ここで示した標準形の組み合わせに変形して計算する。
\(\text{(3)}\) は \(\text{(2)}\) と大きく異なるように見える: 二つの等式の間の関係を理解するには、第十章まで読み進めなければならない。
§136 \((λ x + μ)/\sqrt{ax^{2} + 2bx + c}\) の積分
これまでの結果を使えば、全ての場合についてこの積分を計算できる。次のように議論するのが最も分かりやすいだろう。 \[ \begin{gathered} \lambda x + \mu = \frac{\lambda}{a} (ax + b) + \mu - \frac{\lambda b}{a},\quad \int \frac{ax + b}{\sqrt{ax^{2} + 2bx + c}}\, dx = \sqrt{ax^{2} + 2bx + c} \end{gathered} \] から次の等式が分かる: \[ \int \frac{(\lambda x + \mu)\, dx}{\sqrt{ax^{2} + 2bx + c}} = \frac{\lambda}{a} \sqrt{ax^{2} + 2bx + c} + \left(\mu - \frac{\lambda b}{a}\right) \int \frac{dx}{\sqrt{ax^{2} + 2bx + c}} \]
最後の積分では \(a\) が正にも負にもなる。\(a\) が正なら、\(x\sqrt{a} + (b/\sqrt{a}) = t\) とすれば \[ \frac{1}{\sqrt{a}} \int \frac{dt}{\sqrt{t^{2} + \kappa}} \] を得る。ここで \(\kappa = (ac - b^{2})/a\) である。\(a\) が負なら、\(A = -a\) として \(x\sqrt{A} - (b/\sqrt{A}) = t\) とすれば次を得る: \[ \frac{1}{\sqrt{-a}}\int \frac{dt}{\sqrt{-\kappa - t^{2}}} \]
よっていずれの場合でも、\(\displaystyle \frac{\lambda x + \mu}{\sqrt{ax^{2} + 2bx + c}}\) 積分の計算は §135 で考えた積分の計算に帰着でき、さらにそれは次の三つのどれかに帰着される: \[ \int \frac{dt}{\sqrt{t^{2} + a^{2}}},\quad \int \frac{dt}{\sqrt{t^{2} - a^{2}}},\quad \int \frac{dt}{\sqrt{a^{2} - t^{2}}} \]
§137 \((λ x + μ) \sqrt{ax^{2} + 2bx + c}\) の積分
全く同じやり方で \[ \begin{array}{l} \displaystyle \int(\lambda x + \mu) \sqrt{ax^{2} + 2bx + c}\, dx \\ \displaystyle \quad = \left(\frac{\lambda}{3a}\right) (ax^{2} + 2bx + c)^{3/2} + \left(\mu - \frac{\lambda b}{a}\right) \int \sqrt{ax^{2} + 2bx + c}\, dx \end{array} \] が分かる。最後の積分は次の三つのどれかに帰着される: \[ \int \sqrt{t^{2} + a^{2}}\, dt,\quad \int \sqrt{t^{2} - a^{2}}\, dt,\quad \int \sqrt{a^{2} - t^{2}}\, dt \] こういった形の積分を計算するのに便利な積分に関する一般的な定理を新たに紹介する。
§138 部分積分
部分積分 (integration by parts) の定理は §113 で示した積の微分則を言い換えたものに過ぎない。§113 の結果 3 から \[ \int f'(x)F(x)\, dx = f(x)F(x) - \int f(x)F'(x)\, dx \] が分かる。積分したい関数が \(f'(x)F(x)\) という形をしていて、\(f(x)F'(x)\) なら積分できるという状況はあり得る。例えば \(\phi(x) = x\psi(x)\) で \(\psi(x)\) が既知の関数 \(\chi(x)\) の二次導関数なら \[ \int\phi(x)\, dx = \int x\chi''(x)\, dx = x\chi'(x) - \int \chi'(x)\, dx = x\chi'(x) - \chi(x) \] が成り立つ。
部分積分の例として、前節で考えた積分に部分積分を適用しよう。 \[ f(x) = ax + b,\quad F(x) = \sqrt{ax^{2} + 2bx + c} = y \] とすれば \[ \begin{aligned} a\int y\, dx & = (ax + b)y - \int \frac{(ax + b)^{2}}{y}\, dx \\ & = (ax + b)y - a\int y\, dx + (ac - b^{2}) \int \frac{dx}{y} \end{aligned} \] であり、ここから \[ \int y\, dx = \frac{(ax + b)y}{2a} + \frac{ac - b^{2}}{2a} \int \frac{dx}{y} \] が分かる。最後の積分の計算方法は §135 で見た。
-
\(a \gt 0\) として次を示せ: \[ \begin{aligned} \int \sqrt{x^{2} + a^{2}}\, dx & = \dfrac{1}{2}x \sqrt{x^{2} + a^{2}} + \dfrac{1}{2}a^{2} \log \{x + \sqrt{x^{2} + a^{2}}\},\\ \int \sqrt{x^{2} - a^{2}}\, dx & = \dfrac{1}{2}x \sqrt{x^{2} - a^{2}} - \dfrac{1}{2}a^{2} \log |x + \sqrt{x^{2} - a^{2}}|,\\ \int \sqrt{a^{2} - x^{2}}\, dx & = \dfrac{1}{2}x \sqrt{a^{2} - x^{2}} + \dfrac{1}{2}a^{2} \arcsin\frac{x}{a} \end{aligned} \]
-
積分 \(\displaystyle\int \frac{dx}{\sqrt{a^{2} - x^{2}}}\) と \(\displaystyle\int \sqrt{a^{2} - x^{2}}\, dx\) を置換 \(x = a\sin\theta\) を使って計算し、§135 および問題 1 の結果と一致することを確認せよ。
-
\(\displaystyle\int x(x + a)^{m}\, dx\) を計算せよ。ここで \(m\) は有理数とする。部分積分を使う方法、置換 \((x + a)^{m} = t\) を使う方法、\(x = (x + a) - a\) という書き換えを使う方法の三種類の方法で計算し、結果が一致することを確かめよ。
-
置換 \(ax + b = \dfrac{1}{t}\) と \(x = \dfrac{1}{u}\) を使って次を示せ: \[ \int \frac{dx}{y^{3}} = \frac{ax + b}{\Delta y},\quad \int \frac{x\, dx}{y^{3}} = -\frac{bx + c}{\Delta y} \] \(y\) と \(\Delta\) は §130 および §138 と同じ意味を持つとする。
-
\(b \gt a \) に対する \(\displaystyle\int \frac{dx}{\sqrt{(x - a) (b - x)}}\) を計算せよ。前節の方法、置換 \((b - x)/(x - a) = t^{2}\) を使う方法、置換 \(x = a\cos^{2}\theta + b\sin^{2}\theta\) を使う方法の三種類の方法で計算し、結果が一致することを確かめよ。
-
\(\sqrt{(x - a) (b - x)}\) と \(\sqrt{(b - x)/(x - a)}\) の積分を計算せよ。
-
置換 \(2x + a + b = \frac{1}{2}(a - b) \{t^{2} + (1/t)^{2}\}\) または分母と分子に \(\sqrt{x + a} -\sqrt{x + b}\) を乗じる方法を使って、\(a \gt b\) なら \[ \int \frac{dx}{\sqrt{x + a} + \sqrt{x + b}} = \dfrac{1}{2}\sqrt{a - b} \left(t + \frac{1}{3t^{3}}\right) \] だと示せ。
-
積分 \(\displaystyle\int \frac{dx}{(x + a)^{3/2} + (x - a)^{3/2}}\) を有理関数の積分に簡略化する置換を求めよ。
(Math. Trip. 1899.)
-
積分 \(\displaystyle\int R\{x, \sqrt[n]{ax + b}\}\, dx\) は置換 \(ax + b = y^{n}\) を使って有理関数の積分に簡略化できることを示せ。
-
次を示せ: \[ \int f''(x) F(x)\, dx = f'(x) F(x) - f(x) F'(x) + \int f(x) F''(x)\, dx \] さらに一般的に次を示せ: \[ \begin{array}{l} \displaystyle \int f^{(n)}(x) F(x)\, dx \\ \displaystyle \qquad = f^{(n-1)}(x) F(x) - f^{(n-2)}(x) F'(x) + \cdots + (-1)^{n} \int f(x) F^{(n)}(x)\, dx \end{array} \]
-
有理数 \(p,\ q\) に対する積分 \(\displaystyle\int (1 + x)^{p} x^{q}\, dx\) が求まる場合が三つある: (i) \(p\) が整数の場合、(ii) \(q\) が整数の場合、(iii) \(p + q\) が整数の場合である。 [(i) では \(q\) の分母を \(s\) として \(x = u^{s}\) と置換する。(ii) では \(p\) の分母を \(s\) として \(1 + x = t^{s}\) と置換する。(iii) では \(p\) の分母を \(s\) として \(1 + x = xt^{s}\) と置換する]
-
積分 \(\displaystyle\int x^{m}(ax^{n} + b)^{q}\, dx\) は置換 \(ax^{n} = bt\) で前問の積分に帰着できる。 [実際にこの種の積分を計算するときには "帰着の公式" を使うのが最も簡単である (参考: 第六章に関するその他の例 39)]
-
積分 \(\displaystyle\int R\{x, \sqrt{ax + b}, \sqrt{cx + d}\}\, dx\) は次の置換で有理関数の積分に帰着できる: \[ 4x = -\frac{b}{a} \left(t + \frac{1}{t}\right)^{2} - \frac{d}{c}\left(t - \frac{1}{t}\right)^{2} \]
-
\(y^{2}(x - y) = x^{2}\) のとき積分 \(\displaystyle\int R(x, y)\, dx\) を有理関数の積分に変形せよ。 [\(y = tx\) とすれば \(x = \dfrac{1}{t^{2}(1 - t)},\ y = \dfrac{1}{t(1 - t)}\) を得る]
-
\(y(x - y)^{2} = x\) あるいは \((x^{2} + y^{2})^{2} = a^{2}(x^{2} - y^{2})\) が成り立つとしたときの、前問と同じ積分の有理関数の積分への帰着をそれぞれ示せ。 [前者では \(x - y = t\) とし、後者では \(x^{2} + y^{2} = t(x - y)\) とする。後者では次の関係が得られる: \[ x = \frac{a^{2}t(t^{2} + a^{2})}{t^{4} + a^{4}},\quad y = \frac{a^{2}t(t^{2} - a^{2})}{t^{4} + a^{4}}] \]
-
\(y(x - y)^{2} = x\) なら \[ \int \frac{dx}{x - 3y} = \dfrac{1}{2} \log\{(x - y)^{2} - 1\} \] が成り立つ。
-
\((x^{2} + y^{2})^{2} = 2c^{2}(x^{2} - y^{2})\) なら \[ \int \frac{dx}{y(x^{2} + y^{2} + c^{2})} = - \frac{1}{c^{2}}\log\left(\frac{x^{2} + y^{2}}{x - y}\right) \] が成り立つ。
§139 \(y^{2} = ax^{2} + 2bx + c\) における積分 \(∫ R(x, y), dx\)
特殊な双曲線 \(y^{2} = ax^{2} + 2bx + c\) で関連付いた変数に対する §134 で考えた積分の最も一般的な形を考える。つまり \(X = y^{2} = ax^{2} + 2bx + c\) としたときの \[ \int R(x, \sqrt{X})\, dx \qquad \text{(1)} \] である。\(R\) は実有理関数とする。
被積分関数は \(x\) と \(\sqrt{X}\) の多項式 \(P\) と \(Q\) を使って \(P/Q\) と書ける。よって \(A,\ B,\ \ldots\) を \(x\) の有理関数とすれば \[ \frac{A + B\sqrt{X}}{C + D\sqrt{X}} = \frac{(A + B\sqrt{X})(C - D\sqrt{X})}{C^{2} - D^{2}X} = E + F\sqrt{X} \] という形まで簡略化できる。ここで新しく生じる問題は \(F\sqrt{X}\) の積分である。この問題は \(x\) の有理関数 \(G\) に対する \(G/\sqrt{X}\) の積分と考えることもできる。そして \[ \int \frac{G}{\sqrt{X}}\, dx \qquad \text{(2)} \] は \(G\) を部分分数に分解すれば必ず計算できる。この計算では三種類の積分が生じる。
-
まず、正の整数 \(m\) に対する \[ \int \frac{x^{m}}{\sqrt{X}}\, dx \qquad \text{(3)} \] という積分が生じる可能性がある。\(m = 0\) と \(m = 1\) の場合は §136 で既に議論した。それより大きい \(m\) に対するこの積分を計算するには、次の関係を使う: \[ \begin{aligned} \frac{d}{dx}(x^{m-1}\sqrt{X}) & = (m - 1)x^{m-2} \sqrt{X} + \frac{(ax + b) x^{m-1}}{\sqrt{X}} \\ & = \frac{\alpha x^{m} + \beta x^{m-1} + \gamma x^{m-2}}{\sqrt{X}} \end{aligned} \] ここで \(\alpha,\ \beta,\ \gamma,\ \) は定数であり、その値は簡単に求められる。この等式の両辺を積分すれば、\(\text{(3)}\) の形をした積分の隣り合う三項に関する関係が得られる。\(m = 0\) と \(m = 1\) に対する積分は計算できているから、この関係を使えば他の \(m\) に対する積分も計算できる。
-
第二の可能性として \[ \int \frac{dx}{(x - p)^{m}\sqrt{X}} \qquad \text{(4)} \] という形の積分が考えられる。\(m - p = \dfrac{1}{t}\) と置換すれば、この積分は \(\text{(3)}\) の形をした \(t\) に関する積分となる。
-
最後に、\(G\) の分母の複素根に対応する項の積分が考えられる。複素根が単純な根である一番単純な場合だけを考える。このとき (§138 のように) \(G\) の共役な根の組に対応する項が次の形の積分となる: \[ \int \frac{Lx + M}{(Ax^{2} + 2Bx + C) \sqrt{ax^{2} + 2bx + c}}\, dx \qquad \text{(5)} \]
この積分を計算するには \[ x = \frac{\mu t + \nu}{t + 1} \] という置換を使う。ここで \(\mu\) と \(\nu\) は次の関係が成り立つように選ぶ: \[ a\mu\nu + b(\mu + \nu) + c = 0,\quad A\mu\nu + B(\mu + \nu) + C = 0 \] このとき \(\mu\) と \(\nu\) は次の方程式の根となる: \[ (aB - bA)\xi^{2} - (cA - aC)\xi + (bC - cB) = 0 \] この方程式は 例 46.12 の式 \(\text{(1)}\) と同じ形をしているので、実根を持つ。よってこの条件を満たす実数 \(\mu\) と \(\nu\) は確かに存在する。
置換を代入すれば、\(\text{(5)}\) の積分が \[ H\int \frac{t\, dt}{(\alpha t^{2} + \beta)\sqrt{\gamma t^{2} + \delta}} + K\int \frac{dt}{(\alpha t^{2} + \beta)\sqrt{\gamma t^{2} + \delta}}. \qquad \text{(6)} \] という形になると分かる。二番目の積分は \[ \frac{t}{\sqrt{\gamma t^{2} + \delta}} = u \] と置換すると有理化でき、 \[ \int \frac{dt}{(\alpha t^{2} + \beta) \sqrt{\gamma t^{2} + \delta}} = \int \frac{du}{\beta + (\alpha\delta - \beta\gamma) u^{2}} \] となる。最後に \(\text{(6)}\) の最初の積分は \(t = 1/u\) とすれば二番目の積分となり、ここで説明した方法で計算できる。行う置換は \(\dfrac{u}{\sqrt{\gamma + \delta u^{2}}} = v\) つまり \(\dfrac{1}{\sqrt{\gamma t^{2} + \delta}} = v\) である8。
-
次の積分を計算せよ: \[ \int \frac{dx}{x \sqrt{x^{2} + 2x + 3}},\quad \int \frac{dx}{(x - 1) \sqrt{x^{2} + 1}},\quad \int \frac{dx}{(x + 1) \sqrt{1 + 2x - x^{2}}} \]
-
次の等式を示せ: \[ \int \frac{dx}{(x - p) \sqrt{(x - p) (x - q)}} = \frac{2}{q - p} \sqrt{\frac{x - q}{x - p}} \]
-
\(ag^{2} + ch^{2} = -\nu \lt 0\) なら \[ \int \frac{dx}{(hx + g) \sqrt{ax^{2} + c}} = -\frac{1}{\sqrt{\nu}} \arctan\left[ \frac{\sqrt{\nu(ax^{2} + c)}}{ch - agx} \right] \] が成り立つ。
-
\(y^{2} = ax^{2} + 2bx + c\) のとき \(\displaystyle\int \frac{dx}{(x - x_{0})y}\) が次のいずれかの形で表せることを示せ: \[ -\frac{1}{y_{0}} \log\left| \frac{axx_{0} + b(x + x_{0}) + c + yy_{0}}{x - x_{0}} \right|,\quad \frac{1}{z_{0}} \arctan \left\{ \frac{axx_{0} + b(x + x_{0}) + c}{yz_{0}} \right\} \] \(ax_{0}^{2} + 2bx_{0} + c\) が正なら前者となり、\(y_{0}^{2}\) がその値に等しくなる。\(ax_{0}^{2} + 2bx_{0} + c\) が負なら後者となり、\(-z_{0}^{2}\) がその値に等しくなる。
-
置換 \(y = \dfrac{\sqrt{ax^{2} + 2bx + c}}{x - p}\) を使って次を示せ: \[ \int \frac{dx}{(x - p) \sqrt{ax^{2} + 2bx + c}} = \int \frac{dy}{\sqrt{\lambda y^{2} - \mu}} \] ここで \(\lambda = ap^{2} + 2bp + c\) および \(\mu = ac - b^{2}\) とする。 [この帰着は美しいが、§139 で説明したものより入り組んでいる]
-
積分 \[ \int \frac{dx}{x \sqrt{3x^{2} + 2x + 1}} \] が置換 \(x = \dfrac{1 + y^{2}}{3 - y^{2}}\) で有理化できると示せ。
(Math. Trip. 1911.)
-
次の積分を計算せよ: \[ \int \frac{(x + 1)\, dx}{(x^{2} + 4) \sqrt{x^{2} + 9}} \]
-
次の積分を計算せよ: \[ \int \frac{dx}{(5x^{2} + 12x + 8) \sqrt{5x^{2} + 2x - 7}} \]
[§139 の方法を適用する。\(\mu\) と \(\nu\) が満たす等式は \(\xi^{2} + 3\xi + 2 = 0\) であり、ここから \(\mu = -2\) と \(\nu = -1\) および置換 \(x = -\dfrac{2t + 1}{t + 1}\) が分かる。この置換により積分は \[ -\int \frac{dt}{(4t^{2} + 1) \sqrt{9t^{2} - 4}} - \int \frac{t\, dt}{(4t^{2} + 1) \sqrt{9t^{2} - 4}} \] となる。一つ目の積分では \(\dfrac{t}{\sqrt{9t^{2} - 4}} = u\) とすれば有理化でき、二つ目の積分では \(\dfrac{1}{\sqrt{9t^{2} - 4}} = v\) とすれば有理化できる]
-
次の積分を計算せよ: \[ \int \frac{(x + 1)\, dx}{(2x^{2} - 2x + 1) \sqrt{3x^{2} - 2x + 1}},\quad \int \frac{(x - 1)\, dx}{(2x^{2} - 6x + 5) \sqrt{7x^{2} - 22x + 19}} \]
(Math. Trip. 1911.)
-
\(y^{2} = ax^{2} + 2bx + c\) のときの積分 \(\displaystyle\int R(x, y)\, dx\) が置換 \(t = (x - p)/(y + q)\) によって有理化できると示せ。ここで \((p, q)\) は円錐曲線 \(y^{2} = ax^{2} + 2bx + c\) 上の任意の点とする。 [もちろんこの積分は \(t = (x - p)/(y - q)\) でも有理化できる。§134 を参照]
§140 超越関数の積分
超越関数には非常に多くの種類があるので、その積分は有理関数や代数関数の積分ほどには体系的に行えない。ここでは積分が必ず見つかる超越関数のクラスを順にいくつか見ていく。
§141 サインとコサインの多項式の積分
関数が次の形をした項の有限個の和なら、必ず積分を計算できる: \[ A\cos^{m} ax \sin^{m'} ax \cos^{n} bx \sin^{n'} bx\cdots \] ここで \(m,\ m',\ n,\ n',\ \ldots\) は正の整数で、\(a,\ b,\ \ldots\) は実数とする。この形の項は次の形をした項の和として表せる: \[ \alpha\cos\{(pa + qb + \cdots)x\},\quad \beta \sin\{(pa + qb + \cdots)x\} \] ここから積分もすぐに分かる。
-
\(\sin^{3} x \cos^{2} 2x\) の積分を計算する。この場合には等式 \[ \sin^{3} x = \dfrac{1}{4}(3\sin x - \sin 3x),\quad \cos^{2} 2x = \dfrac{1}{2}(1 + \cos 4x) \] を使う。二つの式を乗じて \(\sin x \cos 4x\) を例えば \(\frac{1}{2}(\sin 5x - \sin 3x)\) と置き換えれば \[ \begin{array}{l} \displaystyle \dfrac{1}{16}\int (7\sin x - 5\sin 3x + 3\sin 5x - \sin 7x)\, dx\\ \displaystyle \qquad \qquad = - \dfrac{7}{16}\cos x + \dfrac{5}{48}\cos 3x - \dfrac{3}{80}\cos 5x + \dfrac{1}{112}\cos 7x \end{array} \] を得る。
積分を違う形で計算する方法も当然ある。例えば \[ \int \sin^{3}x \cos^{2}2x\, dx = \int(4\cos^{4}x - 4\cos^{2}x + 1) (1 - \cos^{2} x)\sin x\, dx \] は置換 \(\cos x = t\) を使えば \[ \int(4t^{6} - 8t^{4} + 5t^{2} - 1)\, dt = \dfrac{4}{7}\cos^{7} x - \dfrac{8}{5}\cos^{5}x + \dfrac{5}{3}\cos^{3}x - \cos x \] に帰着できる。この式が一つ前の計算結果と定数分だけ異なることも確認できるだろう。
-
関数 \[ \cos^{2}x,\quad \sin^{3}x,\quad \cos^{4}x,\quad \cos ax \cos bx,\quad \sin ax \sin bx, \] \[ \cos ax \sin bx,\quad \cos^{3}2x \sin^{2}3x,\quad \cos^{5}x \sin^{7}x,\quad \cos x \cos 2x \cos 3x \] の積分を好きな方法で計算せよ。 [この種の積分では帰着の公式を使った方が簡単な場合もある (第六章に関するその他の例 39)]
§142 \(x^{n} \cos x\) と \(x^{n} \sin x\) の積分
部分積分を使うと上述の結果を一般化できる。等式 \[ \begin{alignedat}{3} \int x^{n}\cos x\, dx & = & & x^{n}\sin x & & - n\int x^{n-1}\sin x\, dx,\\ \int x^{n}\sin x\, dx & = & - & x^{n}\cos x & & + n\int x^{n-1}\cos x\, dx \end{alignedat} \] が成り立つから、この処理を繰り返すことで正の整数 \(n\) に対するこの積分を完全に計算できる。つまり \(\displaystyle\int x^{n}\cos ax\, dx\) と \(\displaystyle\int x^{n}\sin ax\, dx\) は \(n\) が正の整数のとき計算できる。さらに多項式 \(P\) に対する \[ \int P(x, \cos ax, \sin ax, \cos bx, \sin bx,\ \ldots)\, dx \] も同様の方法で計算できる。
-
関数 \[ x\sin x,\quad x^{2}\cos x,\quad x^{2}\cos^{2}x, \] \[ x^{2}\sin^{2}x \sin^{2} 2x,\quad x\sin^{2}x \cos^{4}x,\quad x^{3}\sin^{3}\frac{1}{3}x \] の積分を計算せよ。
-
次の条件を満たす多項式 \(P,\ Q\) を求めよ: \[ \int\{(3x - 1)\cos x + (1 - 2x)\sin x\}\, dx = P\cos x + Q\sin x \]
-
\(\displaystyle\int x^{n}\cos x\, dx = P_{n}\cos x + Q_{n}\sin x\) を示せ。ここで \[ \begin{aligned} P_{n} & = nx^{n-1} - n(n - 1)(n - 2) x^{n-3} + \cdots,\\ Q_{n} & = x^{n} - n(n - 1) x^{n-2} + \cdots \end{aligned} \] とする。
§143 \(\cos x\) と \(\sin x\) の有理関数の積分
\(\cos x\) と \(\sin x\) の有理関数の積分は置換 \(\tan \frac{1}{2} = t\) を使うと計算できる。等式 \[ \cos x = \frac{1 - t^{2}}{1 + t^{2}},\quad \sin x = \frac{2t}{1 + t^{2}},\quad \frac{dx}{dt} = \frac{2}{1 + t^{2}} \] が成り立つので、積分は \(t\) の有理関数の積分に帰着される。
-
次を示せ: \[ \int \sec x\, dx = \log |\sec x + \tan x|,\quad \int \cosec x\, dx = \log |\tan \dfrac{1}{2}x| \]
-
次が成り立つ: \[ \begin{gathered} \int \tan x\, dx = -\log |\cos x|,\ \int \cot x\, dx = \log |\sin x|,\\ \int\sec^{2} x\, dx = \tan x,\ \int \cosec^{2} x\, dx = -\cot x,\\ \int \tan x\sec x\, dx = \sec x,\ \int \cot x \cosec x\, dx = -\cosec x \end{gathered} \]
[積分はどれも一般的な形に含まれるが、置換を使う必要はない。§119 と §130 の式 \(\text{(5)}\) からすぐに分かる]
-
\(a + b\) が正のとき、\(\dfrac{1}{a + b\cos x}\) の積分が次の形をしていると示せ: \[ \frac{2}{\sqrt{a^{2} - b^{2}}} \arctan \left\{t\sqrt{\frac{a - b}{a + b}}\right\},\quad \frac{1}{\sqrt{b^{2} - a^{2}}} \log \left|\frac{\sqrt{b + a} + t\sqrt{b - a}} {\sqrt{b + a} - t\sqrt{b - a}}\right| \] ここで \(t = \tan\frac{1}{2}x\) とする。\(a^{2} \gt b^{2}\) なら前者となり、\(a^{2} \lt b^{2}\) なら後者となる。\(a^{2} = b^{2}\) なら積分は \(\sec^{2}\frac{1}{2}x\) または \(\cosec^{2}\frac{1}{2}x\) の定数倍となり、その係数は簡単に計算できる。\(a + b\) が負のときの積分の形を示せ。
-
次の等式で定義される \(x\) の関数 \(y\) を考える: \[ (a + b\cos x)(a - b\cos y) = a^{2} - b^{2} \] ただし \(a\) は正で \(a^{2} \gt b^{2}\) とする。このとき \(x\) が \(0\) から \(\pi\) まで動くなら、\(y\) の値の一つも \(0\) から \(\pi\) まで動くと示せ。また \[ \sin x = \frac{\sqrt{a^{2} - b^{2}} \sin y}{a - b\cos y},\quad \frac{\sin x}{a + b\cos x}\, \frac{dx}{dy} = \frac{\sin y}{a - b\cos y} \] であることを示し、これを使って \(0 \lt x \lt \pi\) で次の等式が成り立つと示せ: \[ \int \frac{dx}{a + b\cos x} = \frac{1}{\sqrt{a^{2} - b^{2}}} \arccos \left(\frac{a\cos x + b}{a + b\cos x}\right) \]
この結果が問題 3 と一致することを確かめよ。
-
\(\dfrac{1}{a + b\cos x + c\sin x}\) の積分の計算する方法を示せ。
[\(b\cos x + c\sin x\) を \(\sqrt{b^{2} + c^{2}} \cos(x - \alpha)\) の形で表す]
-
\(\dfrac{a + b\cos x + c\sin x}{\alpha + \beta\cos x + \gamma\sin x}\) の積分を計算せよ。
[次の条件が成り立つように \(\lambda,\ \mu,\ \nu\) を定める: \[ a + b\cos x + c\sin x = \lambda + \mu(\alpha + \beta\cos x + \gamma\sin x) + \nu(-\beta\sin x + \gamma\cos x) \] このとき求める積分は \[ \mu x + \nu \log |\alpha + \beta\cos x + \gamma\sin x| + \lambda \int \frac{dx}{\alpha + \beta\cos x + \gamma\sin x} \] となる]
-
\(\dfrac{1}{a\cos^{2} x + 2b\cos x\sin x + c\sin^{2} x}\) の積分を計算せよ。
[被積分関数は \(\dfrac{1}{A + B\cos 2x + C\sin 2x}\) と変形できる。ここで \(A = \frac{1}{2}(a + c),\ \) \(B = \frac{1}{2}(a - c),\ \) \(C = b\) である。あるいは \(\tan x = t\) と置換すれば次を得る: \[ \int \frac{\sec^{2} x\, dx}{a + 2b\tan x + c\tan^{2} x} = \int \frac{dt}{a + 2bt + ct^{2}} \]
§144 \(\arcsin x,\ \arctan x,\ \log x\) を含む式の積分
サインとタンジェントの逆関数および対数関数の積分は部分積分を使って簡単に求められる。結果を次に示す: \[ \begin{aligned} \int \arcsin x\, dx & = x\arcsin x - \int \frac{x\, dx}{\sqrt{1 - x^{2}}} = x\arcsin x + \sqrt{1 - x^{2}},\\ \int \arctan x\, dx & = x\arctan x - \int \frac{x\, dx}{1 + x^{2}} = x\arctan x - \dfrac{1}{2} \log(1 + x^{2}),\\ \int \log x\, dx & = x\log x - \int dx = x(\log x - 1) \end{aligned} \]
\(y = f(x)\) の積分が求まるときに \(f\) の逆関数 \(\phi\) に対する \(x = \phi(y)\) の積分も必ず求められることを示すのは難しくない。置換 \(y = f(x)\) を使えば \[ \int \phi(y)\, dy = \int xf'(x)\, dx = xf(x) - \int f(x)\, dx \] が分かる。この方法を使って \(\arcsin y\) と \(\arctan y\) の積分を計算してみるとよい。
また多項式 \(P\) に対する \[ \int P(x, \arcsin x)\, dx,\quad \int P(x, \log x)\, dx \] という形の積分は必ず計算できる。例えば一つ目の形の積分では \(\displaystyle\int x^{m} (\arcsin x)^{n}\, dx\) という項を計算する必要があるが、\(x = \sin y\) と置換すると \(\displaystyle\int y^{n}\sin^{m}y \cos y\, dy\) となり、§142 の方法で求められる。二番目の形の積分では \(\displaystyle\int x^{m} (\log x)^{n}\, dx\) という形の項を計算する必要があるが、部分積分を使うと \[ \int x^{m}(\log x)^{n}\, dx = \frac{x^{m+1} (\log x)^{n}}{m + 1} - \frac{n}{m + 1} \int x^{m}(\log x)^{n-1}\, dx \] が分かるので、この変形を繰り返せば最終的には必ず積分の値を求められる。
§145 平面曲面の面積
ここまで説明してきた積分の最も重要な応用は、平面曲線の面積の計算である。連続曲線 \(y = \phi(x)\) のグラフ \(P_{0}PP'\) (図 44) が \(x\) 軸の上方にあると仮定し、\(P\) が点 \((x, y)\) で \(P'\) が点 \((x + h, y + k)\) だとする。\(h\) は正でも負でもよい (図では正としている)。
読者は「面積」の意味を当然知っており、特に「\(ONPP_{0}\) の面積」と言ったときに何を意味するかを知っていると思う。ここでは面積という概念が数学的な定義なしに定められているものとする。実は "面積" は最も詳細な数学的解析を必要とする概念であり、これまでにたくさんの解析がなされてきた。以降の章ではこの問題に立ち返り、\(ONPP_{0}\) などの領域の「面積」が正確に何を意味するのかを説明する。ただ今の段階では、そういった領域にとある正の実数 \((ONPP_{0})\) が対応付いているのだと単純に仮定して話を進める。この実数は面積と呼ばれ、次に示すような常識的に明らかな性質を持つ: \[ (PRP') + (NN'RP) = (NN'P'P),\quad (N_{1}NPP_{1}) \lt (ONPP_{0}) \]
こういった仮定の下で \(ONPP_{0}\) が \(x\) の関数となるのは明らかである。これを \(\Phi(x)\) と表記する。次の関係が成り立つので、\(\Phi(x)\) が 連続関数だとも分かる: \[ \begin{aligned} \Phi(x + h) - \Phi(x) & = (NN'P'P)\\ & = (NN'RP) + (PRP') = h\phi(x) + (PRP') \end{aligned} \]
今考えている図では \(PRP'\) の面積は \(hk\) より小さいが、これは常に成り立つわけではない。弧 \(PP'\) が \(P\) から \(P'\) に向かうときに単調に増加あるいは減少するとは限らないためである (例えば 図 44a)。しかし \(\lambda(h)\) を \(PR\) から \(PP'\) 上の任意の点への距離の最大値とすれば、\(PRP'\) の面積は \(|h|\lambda(h)\) より小さくなる。また \(\phi(x)\) は連続関数だから、\(h \to 0\) のとき \(\lambda(h) \to 0\) が成り立つ。よって \[ \Phi(x + h) - \Phi(x) = h\{\phi(x) + \mu(h)\} \] となる。ここで \(|\mu(h)| \lt \lambda(h)\) かつ \(h \to 0\) のとき \(\lambda(h) \to 0\) である。この式からも \(\Phi(x)\) が連続だと直ちに分かる。さらに \[ \Phi'(x) = \lim_{h \to 0} \frac{\Phi(x + h) - \Phi(x)}{h} = \lim_{h \to 0} \{\phi(x) + \mu(h)\} = \phi(x) \] だから、曲線の \(\bm{y}\) 座標は面積の導関数で、曲線の \(\bm{y}\) 座標の積分は面積となる。
以上の議論から \(ONPP_{0}\) の面積を計算する方法が定式化できる: まず \(\phi(x)\) の積分 \(\Phi(x)\) を計算する。\(\Phi(x)\) には任意定数が含まれるから、\(\Phi(0) = 0\) となるようにそれを選ぶ。すると求める面積は \(\Phi(x)\) となる。
求める面積が \(N_{1}NPP_{1}\) なら、\(P_{1}\) の \(x\) 座標を \(x_{1}\) として \(\Phi(x_{1}) = 0\) が成り立つように定数を定める必要がある。あるいはもし曲線が \(x\) 軸の下方にあるなら \(\Phi(x)\) が負になるので、\(\Phi(x)\) の絶対値が面積となる。
§146 平面曲線の長さ
直線でない曲線の長さは、実は面積よりも難しい概念となる。図 44 において \(P_{0}P\) が有限の長さ \(S(x)\) を持つという仮定からは (面積で行ったような) 満足行く議論が行えない。そもそも \(S(x)\) が連続である、つまり \(\lim\{S(P') - S(P)\} = 0\) であることさえ証明できない。図 44 ではこれが明らかに成り立つように思えるが、図 44a ではそうとも言えない。実は曲線の長さが意味するものを注意深く解析しない限り、いくらかでも厳密さを持った議論は行えない。
ただ曲線の長さを表す式がどのような形にならなければならないかは簡単に分かる。曲線が接線を持ち、その傾きが連続的に変化すると仮定する。このとき \(\phi'(x)\) は連続となる。すると曲線が長さを持つという仮定から \[ \frac{S(x + h) - S(x)}{h} = \frac{\{PP'\}}{h} = \frac{PP'}{h} × \frac{\{PP'\}}{PP'} \] が分かる。ここで \(\{PP'\}\) は弦 \(PP'\) に対応する弧の長さを表す。さて \[ PP' = \sqrt{PR^{2} + {RP'}^{2}} = h\sqrt{1 + \frac{k^{2}}{h^{2}}} \] だから、\(x\) と \(x + h\) の間にある \(\xi\) で \[ k = \phi(x + h) - \phi(x) = h\phi'(\xi) \] が成り立つ。よって \[ \lim \frac{PP'}{h} = \lim \sqrt{1 + [\phi'(\xi)]^{2}} = \sqrt{1 + [\phi'(x)]^{2}} \] が分かる。加えて \[ \lim \frac{\{PP'\}}{PP'} = 1 \] を仮定すれば、 \[ S'(x) = \lim \frac{S(x + h) - S(x)}{h} = \sqrt{1 + [\phi'(x)]^{2}} \] および \[ S(x) = \int \sqrt{1 + [\phi'(x)]^{2}}\, dx \] が分かる。
-
放物線 \(y = \dfrac{x^{2}}{4a}\) を \(y = \xi\) で切ったときに残る部分の面積およびそれを囲む弧の長さを求めよ。
-
曲線 \(ay^{2} = x^{3}\) について前問と同じ問いに答えよ。弧の長さは \[ \frac{8a}{27} \left\{\left(1 + \frac{9\xi}{4a}\right)^{3/2} - 1\right\} \] となる。
-
円 \(x^{2} + y^{2} = a^{2},\ x^{2} + y^{2} = 2ax\) の長さと面積を §145–§146 の公式を使って求めよ。
-
楕円 \(\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} = 1\) の面積が \(\pi ab\) だと示せ。
-
\(y = \sin x\) と \(x\) 軸の \(x = 0\) から \(x = 2\pi\) の部分が囲む領域の面積を求めよ。 [この問題では \(\Phi(x) = -\cos x\) であり、\(x = 0\) と \(x = -2\pi\) おける \(-\cos x\) の値の差が \(0\) となる。なぜこうなるかというと、\(x = \pi\) から \(x = 2\pi\) で曲線が \(x\) 軸の下方にあるためである。つまりこの方法で計算すると、この部分の面積が負としてカウントされてしまう。\(x = 0\) から \(x = \pi\) の領域の面積は \(-\cos \pi + \cos 0 = 2\) であり、全ての部分を正としてカウントした求めるべき全体の面積はこの二倍、つまり \(4\) となる]
-
とある曲線上の任意の点の座標が変数 \(t\) の関数として \(x = \phi(t),\ y = \psi(t)\) と表され、\(\psi(t)\) と \(\phi(t)\) が連続な導関数を持つとする。\(t\) が \(t_{0}\) から \(t_{1}\) へ動くとき \(x\) が単調に増加するなら、曲線の対応する部分と \(x\) 軸および \(x = t_{0}\) と \(x = t_{1}\) で囲まれる部分の面積が、符号を無視すれば、\(A(t_{1}) - A(t_{0})\) に等しくなると示せ。\(A(t)\) は次のように定める: \[ A(t) = \int \psi(t)\phi'(t)\, dt = \int y \frac{dx}{dt}\, dt \]
-
\(C\) が一重のループからなる閉曲線であり、二つの軸のどちらかに平行な任意の直線が \(C\) と多くとも二回しか交わらないとする。さらに問題 6 と同様に曲線上の任意の点 \(P\) が \(t\) を使って表され、\(t\) が \(t_{0}\) から \(t_{1}\) に変化するとき \(P\) は \(C\) を同じ方向に一周して最初の点に戻るとする。\(C\) のループが囲む領域の面積が、次の積分の最初の値と最後の値の差に等しいことを示せ: \[ -\int y \frac{dx}{dt}\, dt,\quad \int x \frac{dy}{dt}\, dt,\quad \dfrac{1}{2} \int \left(x \frac{dy}{dt} - y \frac{dx}{dt}\right) dt \] もちろん差は正とする。
-
問題 7 の結果を使って次の曲線の面積を求めよ: \[ \text{(i) } \frac{x}{a} = \frac{1 - t^{2}}{1 + t^{2}},\quad \frac{y}{a} = \frac{2t}{1 + t^{2}},\qquad \text{(ii) } x = a\cos^{3} t,\quad y = b\sin^{3} t \]
-
曲線 \(x^{3} + y^{3} = 3axy\) のループの面積を求めよ。 [\(y = tx\) とすれば \(x = 3at/(1 + t^{3}),\ y = 3at^{2}/(1 + t^{3})\) が成り立つ。\(t\) が \(0\) から \(\infty\) まで変化すると、点はループを一度だけ周回する。そして \[ \begin{aligned} \dfrac{1}{2} \int \left(y \frac{dx}{dt} - x \frac{dy}{dt}\right)\, dt & = -\dfrac{1}{2} \int x^{2} \frac{d}{dt}\left(\frac{y}{x}\right)\, dt \\ & = -\dfrac{1}{2} \int \frac{9a^{2}t^{2}}{(1 + t^{3})^{2}}\, dt \\ & = \frac{3a^{2}}{2(1 + t^{3})} \end{aligned} \] は \(t \to \infty\) で \(0\) に向かう。よってループの面積は \(\frac{3}{2}a^{2}\) である]
-
曲線 \(x^{5} + y^{5} = 5ax^{2}y^{2}\) のループの面積を求めよ。
-
曲線 \(x = a\sin 2t,\ y = a\sin t\) のループの面積が \(\frac{4}{3}a^{2}\) だと示せ。
(Math. Trip. 1908.)
-
\(x = a\cos t,\ y = b\sin t\) で定まる楕円の \(t = t_{1}\) に対応する点から \(t = t_{2}\) に対応する点までの弧の長さは \(F(t_{2}) - F(t_{1})\) で与えられる。ここで \[ F(t) = a\int \sqrt{1 - e^{2}\sin^{2} t}\, dt \] および \(e\) を離心率とする。 [しかしこの積分を今までに出てきた関数を使って表すことはできない]
-
極座標: \(f(\theta)\) を \(\theta\) の一価関数をする。曲線 \(r = f(\theta)\) の \(\theta = \theta_{1}\) から \(\theta = \theta_{2}\) に対応する動径で囲まれる領域の面積が \(\displaystyle F(\theta) = \dfrac{1}{2} \int r^{2}\, d\theta\) を使って \(F(\theta_{2}) - F(\theta_{1})\) と表せること、さらに対応する弧の長さが \[ \Phi(\theta) = {\Large\int} \sqrt{r^{2} + \biggl(\frac{dr}{d\theta}\biggr)^{2}}\, d\theta \] を使って \(\Phi(\theta_{2}) - \Phi(\theta_{1})\) と表せることを示せ。
これを使えば次の値を求められる: (i) 円 \(r = 2a\sin\theta\) の面積と周囲の長さ (ii) 放物線 \(r = \frac{1}{2}l\sec^{2} \frac{1}{2}\theta\) と通径の囲む領域の面積および対応する部分の長さ (iii) パスカルの蝸牛形 \(r = a + b\cos\theta\) の面積 (\(a \gt b,\ a = b,\ a \lt b\) の場合それぞれ) (iv) 楕円 \(1/r^{2} = a\cos^{2} \theta + 2h\cos\theta\sin\theta + b\sin^{2} \theta\) および \(l/r = 1 + e\cos\theta\) の面積。 [最後の面積の計算では積分 \(\displaystyle \int \frac{d\theta}{(1 + e\cos\theta)^{2}}\) が生じるが、これは置換 \[ (1 + e\cos\theta) (1 - e\cos\phi) = 1 - e^{2} \] を使うと計算できる (参考: 例 53.4)]
-
曲線 \(2\theta = \dfrac{a}{r} + \dfrac{r}{a}\) が通る点を調べ、点 \(r = a,\ \theta = 1\) で接する二つの枝と動径 \(\theta = \beta\) で囲まれる領域の面積が \(\frac{2}{3} a^{2}(\beta^{2} - 1)^{3/2}\) だと示せ。
(Math. Trip. 1900.)
-
等式 \(p = f(r)\) によって定義される曲線を考える。\(r\) は動径の長さで、\(p\) は原点から接線に下ろした垂線の長さとする。曲線と二つの動径で囲まれた領域の面積の計算で \(\dfrac{1}{2} \displaystyle \int \frac{pr\, dr}{\sqrt{r^{2} - p^{2}}}\) が必要になることを示せ。
第六章に関するその他の例
-
\(x \leq 0\) で \(1 + x\)、\(0 \lt x \lt 1\) で \(x\)、\(1 \leq x \leq 2\) で \(2 - x\)、\(x \gt 2\) で \(3x - x^{2}\) となる関数を \(f(x)\) とする。\(x = 0,\ 1,\ 2\) における \(f(x)\) の連続性および \(f'(x)\) の存在と連続性を議論せよ。
-
\(a,\ ax + b,\ ax^{2} + 2bx + c,\ \ldots\) をそれぞれ \(u_{0},\ u_{1},\ u_{2},\ \ldots\) と表記する。このとき \(u_{0}^{2} u_{3} - 3u_{0} u_{1} u_{2} + 2u_{1}^{3}\) と \(u_{0} u_{4} - 4u_{1} u_{3} + 3u_{2}^{2}\) が \(x\) によらないと示せ。
-
定数 \(a_{0},\ a_{1},\ \ldots,\ a_{2n}\) に対して \(U_{r} = (a_{0}, a_{1},\ \ldots, a_{r} \mathbin{)\kern-5pt(} x, 1)^{r}\) とする9。このとき \[ U_{0}U_{2n} - 2nU_{1}U_{2n-1} + \frac{2n(2n - 1)}{1·2} U_{2}U_{2n-2} - \cdots + U_{2n}U_{0} \] は \(x\) によらない。 [微分して等式 \(U_{r}' = rU_{r-1}\) を使う]
(Math. Trip. 1896.)
-
\(\mu \gt 1\) なら、\(\arcsin(\mu\sin x) - x\) の一次・二次・三次導関数は全て \(0 \leq x \leq \frac{1}{2} \pi\) で正となる。
-
とある行列の行列式が \(x\) の関数だとする。この行列式の微分係数が、一つの行だけを微分して他の行はそのままにした行列の行列式の和と等しいことを示せ。
-
\(f_{1},\ f_{2},\ f_{3},\ f_{4}\) を次数が \(4\) 以下の多項式とする。このとき \[ \begin{vmatrix} f_{1}& f_{2}& f_{3}& f_{4}\\ f_{1}'& f_{2}'& f_{3}'& f_{4}'\\ f_{1}''& f_{2}''& f_{3}''& f_{4}''\\ f_{1}'''& f_{2}'''& f_{3}'''& f_{4}''' \end{vmatrix} \] も次数が \(4\) 以下の多項式だと示せ。 [行列式を五回微分すると \(0\) になることを問題 5 の結果を使って示す]
-
\(y^{3} + 3yx + 2x^{3} = 0\) なら \(x^{2}(1 + x^{3})y'' - \dfrac{3}{2}xy' + y = 0\) が成り立つ。
(Math. Trip. 1903.)
-
微分方程式 \(y = \phi\{\psi(y_{1})\} + \phi\{x - \psi(y_{1})\}\) が \(y = \phi(c) + \phi(x - c)\) と \(y = 2\phi(\frac{1}{2}x)\) によって満たされることを確認せよ。\(y_{1}\) は \(y\) の導関数、\(\psi\) は \(\phi'\) の逆関数とする。
-
微分方程式 \(y = \{x/\psi(y_{1})\} \phi\{\psi(y_{1})\}\) が \(y = c\phi(x/c)\) と \(y = \beta x\) によって満たされることを確認せよ。\(\beta = \phi(\alpha)/\alpha\) であり、\(\alpha\) は \(\phi(\alpha) - \alpha\phi'(\alpha) = 0\) の任意の根と定める。他の記号は問題 8 と同様とする。
-
\(ax + by + c = 0\) なら \(y_{2} = 0\) が成り立つ (関数に付いた添え字で \(x\) に関する微分の回数を表す)。この事実を全ての直線を表す一般的な微分方程式は \(\bm{y_{2} = 0}\) であると表現する。次の図形を表す一般的な微分方程式を求めよ: (i) 中心が \(x\) 軸上にある全ての円 (ii) 軸が \(x\) 軸に重なる全ての放物線 (iii) 軸が \(y\) 軸と平行な全ての放物線 (iv) 全ての円 (v) 全ての放物線 (vi) 全ての円錐曲線。
[答えの方程式は (i) \(1 + y_{1}^{2} + yy_{2} = 0,\ \) (ii) \(y_{1}^{2} + yy_{2} = 0,\ \) (iii) \(y_{3} = 0,\ \) (iv) \((1 + y_{1}^{2}) y_{3} = 3y_{1} y_{2}^{2},\ \) (v) \(5y_{3}^{2} = 3y_{2} y_{4},\ \) (vi) \(9y_{2}^{2} y_{5} - 45y_{2} y_{3} y_{4} + 40y_{3}^{3} = 0\) である。いずれの場合でも、調べる曲線を表す一般的な方程式を考え、それを任意定数がなくなるまで微分すればそれだけで答えが得られる]
-
全ての放物線および全ての円錐曲線を表す一般的な微分方程式が、それぞれ \[ D_{x}^{2} (y_{2}^{-2/3}) = 0,\quad D_{x}^{3} (y_{2}^{-2/3}) = 0 \] なことを示せ。
[円錐曲線の方程式は \[ y = ax + b ± \sqrt{px^{2} + 2qx + r} \] と書ける。ここから \[ y_{2} = ±\frac{pr - q^{2}}{(px^{2} + 2qx + r)^{3/2}} \] が分かる。放物線では加えて \(p = 0\) が成り立つ]
-
\(\dfrac{dy}{dx},\ \dfrac{1}{2!}\, \dfrac{d^{2}y}{dx^{2}},\ \dfrac{1}{3!}\, \dfrac{d^{3}y}{dx^{3}},\ \dfrac{1}{4!}\, \dfrac{d^{4}y}{dx^{4}},\ \ldots\) を \(t,\ a,\ b,\ c,\ \ldots\) と表記し、\(\dfrac{dx}{dy},\ \dfrac{1}{2!}\, \dfrac{d^{2}x}{dy^{2}},\ \dfrac{1}{3!}\, \dfrac{d^{3}x}{dy^{3}}\), \(\dfrac{1}{4!}\, \dfrac{d^{4}x}{dy^{4}},\ \ldots\) を \(\tau,\ \alpha,\ \beta,\ \gamma,\ \ldots\) と表記する。このとき \[ 4ac - 5b^{2} = \frac{4\alpha\gamma - 5\beta^{2}}{\tau^{8}},\quad bt - a^{2} = - \frac{\beta\tau - \alpha^{2}}{\tau^{6}} \] を示せ。同様の等式を \(a^{2}d - 3abc - 2b^{3},\ (1 + t^{2})b - 2a^{2}t,\ 2ct - 5ab\) に対してそれぞれ求めよ。
-
\(y = \sin(n\arcsin x)\) の \(k\) 次導関数を \(y_{k}\) とする。等式 \[ (1 - x^{2})y_{k+2} - (2k + 1)xy_{k+1} + (n^{2} - k^{2})y_{k} = 0 \] を示せ。
[\(k = 0\) の場合をまず証明し、それからライプニッツの定理を使って \(k\) 回微分する]
-
等式 \[ vD_{x}^{n}u = D_{x}^{n}(uv) - nD_{x}^{n-1}(uD_{x}v) + \frac{n(n - 1)}{1·2} D_{x}^{n-2}(uD_{x}^{2}v) - \cdots \] を示せ。\(n\) は正の整数とする。 [数学的帰納法を使う]
-
次の式で与えられる曲線を考える: \[ \begin{aligned} x & = a(2\cos t + \cos 2t),\quad y & = a(2\sin t - \sin 2t) \end{aligned} \]
次を示せ: (i) パラメータ \(t = t\) に対応する点における接線と法線の方程式が \[ x\sin \dfrac{1}{2} t + y\cos \dfrac{1}{2} t = a\sin \dfrac{3}{2} t,\quad x\cos \dfrac{1}{2} t - y\sin \dfrac{1}{2} t = 3a\cos \dfrac{3}{2} t \] であること (ii) \(P\) における接線が曲線と交わる点 \(Q,\ R\) のパラメータがそれぞれ \(-\frac{1}{2}t\) と \(\pi - \frac{1}{2} t\) であること (iii) \(QR = 4a\) (iv) \(Q\) と \(R\) における接線が直行し、交点が円 \(x^{2} + y^{2} = a^{2}\) 上にあること (v) \(P,\ Q,\ R\) における法線が一点で交わり、交点が円 \(x^{2} + y^{2} = 9a^{2}\) 上にあること (vi) 曲線の方程式が \[ (x^{2} + y^{2} + 12ax + 9a^{2})^{2} = 4a(2x + 3a)^{3} \] であること。
曲線の概形を図示せよ。
-
問題 15 の曲線の定義は \(\xi/a = 2u + (1/u^{2}),\ \eta/a = (2/u) + u^{2}\) と書けることを示せ。\(\xi = x + yi,\ \eta = x - yi\), \(u = \operatorname{Cis} t\) とする。点 \(u\) における接線と法線が \[ u^{2}\xi - u\eta = a(u^{3} - 1),\quad u^{2}\xi + u\eta = 3a(u^{3} + 1) \] だと示し、問題 15 の (ii)–(v) を証明せよ。
-
\(x^{4} + 4px^{3} - 4qx - 1 = 0\) が重根を持つ条件が \((p + q)^{2/3} - (p - q)^{2/3} = 1\) だと示せ。
(Math. Trip. 1898.)
-
三次方程式 \(f(x) = 0\) の根を小さい順に \(\alpha,\ \beta,\ \gamma\) とする。\([\alpha, \beta]\) と \([\beta, \gamma]\) を六等分すると、\(f'(x) = 0\) の根がそれぞれ \(\beta\) から数えて四つ目の小区間に属することを示せ。\(f'(x) = 0\) の根が分割点に一致する場合が二つあるが、このとき三次方程式はどのような性質を持つか?
(Math. Trip. 1907.)
-
次に示す関数を \(f(x)\) として、\(f(x)\) の極大値と極小値および \(f(x) = 0\) の実根を調べよ: \[ \begin{gathered} x - \sin x - \tan\alpha (1 - \cos x),\\ x - \sin x - (\alpha - \sin\alpha) - \tan \dfrac{1}{2}\alpha (\cos\alpha - \cos x) \end{gathered} \] \(\alpha\) は \(0\) から \(\pi\) の角度とする。最初の関数が二重根を持つ条件が「\(\tan\alpha - \alpha\) が \(\pi\) の倍数」だとを示せ。
-
比 \(\lambda : \mu\) を調整することで、\(\lambda(ax^{2} + bx + c) + \mu(a'x^{2} + b'x + c') = 0\) の根を実数とし、その差を任意の値とできることを示せ。ただしこの式に含まれる二つの二次方程式が実根を持ち、その区間が重なる場合は除く。この場合には根が必ず実数となるが、その差に下限が存在する。
(Math. Trip. 1895.)
[関数 \(\dfrac{ax^{2} + bx + c}{a'x^{2} + b'x + c'}\) のグラフの形を考える。例 46.12 などを参照]
-
\(0 \lt x \lt 1\) のとき \[ \pi \lt \frac{\sin \pi x}{x(1 - x)} \leq 4 \] だと示し、この関数のグラフを描け。
-
次の関数のグラフを描け: \[ \pi \cot\pi x - \frac{1}{x} - \frac{1}{x - 1} \]
-
次の微分方程式で定義される \(y\) のグラフの概形を描け: \[ \frac{dy}{dx} = \frac{(6x^{2} + x - 1) (x - 1)^{2} (x + 1)^{3}}{x^{2}} \]
(Math. Trip. 1908.)
-
長方形の紙を折って、角の一つが反対側の辺の上にあるようにする。折り目の長さを極大にする折り方を求めよ。
-
楕円 \(\dfrac{x^{2}}{a^{2}} + \dfrac{y^{2}}{b^{2}} = 1\) と中心が同じ円が交わる鋭角の最大値は \(\arctan\dfrac{a^{2} - b^{2}}{2ab}\) である。
(Math. Trip. 1900.)
-
三角形の面積と \(\Delta\) と周囲の長さの半分 \(s\) が固定されている。いずれかの辺の長さの極大値または極小値が \(s(x - s) x^{2} + 4\Delta^{2} = 0\) を満たすことを示せ。方程式の根の存在、そしてそれが極大値と極小値のどちらなのかについて議論せよ。
[\(a + b + c = 2s\) と \(s(s - a)(s - b)(s - c) = \Delta^{2}\) を使えば \(a\) と \(b\) を \(c\) の関数として表せる。\(c\) に関して微分して \(da/dc = 0\) とすると \(b = c\) かつ \(s - b = s - c = \frac{1}{2} a\) が得られ、ここから \(s(a - s)a^{2} + 4\Delta^{2} = 0\) が得られる。
この方程式は \(s^{4} \gt 27\Delta^{2}\) なら三つの実根を持ち、そうでなければ一つの実根を持つ。三辺が等しいとき (固定された面積に対する周りの長さが極小の三角形のとき) \(s^{4} = 27\Delta^{2}\) が成り立つので、\(s^{4} \lt 27\Delta^{2}\) にはならない。よって上の \(a\) に関する方程式は三つの実根を持つ。さらに三つの根の和が正で積が負だから、二つの根が正でもう一つが負と分かる。二つの正の根のうち一つが極大値に対応し、もう一つが極小値に対応する]
-
与えられた三点 \(A,\ B,\ C\) を通る面積最大の正三角形の面積は \[ 2\Delta + \frac{a^{2} + b^{2} + c^{2}}{2\sqrt{3}} \] である。\(a,\ b,\ c\) は \(\triangle ABC\) の三辺の長さで、\(\Delta\) はその面積とする。
(Math. Trip. 1899.)
-
頂点の一つが原点にあり、底角がカージオイド \(r = a(1 + \cos\theta)\) 上にある二等辺三角形の面積の極大値を \(\Delta,\ \Delta'\) とすると、\(256\Delta\Delta' = 25a^{4}\sqrt{5}\) が成り立つ。
(Math. Trip. 1907.)
-
点 \((x, y)\) が曲線 \(x^{2}y - 4x^{2} - 4xy + y^{2} + 16x - 2y - 7 = 0\) を通って \((2, 3)\) に近づくときの \((x^{2} - 4y + 8)/(y^{2} - 6x + 3)\) の極限を求めよ。
(Math. Trip. 1903.)
[\((2, 3)\) を新しい原点として取ると、曲線の方程式は \(\xi^{2} \eta - \xi^{2} + \eta^{2} = 0\) となり、極限を求める関数の式は \((\xi^{2} + 4\xi - 4\eta)/(\eta^{2} + 6\eta - 6\xi)\) となる。\(\eta = t\xi\) とすると \(\xi = (1 - t^{2})/t,\ \eta = 1 - t^{2}\) を得る。曲線は原点が分岐点となっており、これは \(t = -1\) と \(t = 1\) に対応する。与えられた関数を \(t\) を使って書き直し、\(t\) を \(-1\) あるいは \(1\) に向かわせれば、極限がそれぞれ \(-\frac{3}{2}\) と \(-\frac{2}{3}\) だと分かる]
-
もし \[ f(x) = \dfrac{1}{\sin x - \sin a} - \dfrac{1}{(x - a)\cos a} \] なら \[ \frac{d}{da}\{\lim_{x \to a} f(x)\} - \lim_{x \to a}f'(x) = \dfrac{3}{4} \sec^{3} a - \dfrac{5}{12} \sec a \] が成り立つ。
-
\(\phi(x) = 1/(1 + x^{2})\) なら \(\phi^{n} (x) = Q_{n}(x)/(1 + x^{2})^{n+1}\) だと示せ。\(Q_{n}(x)\) は次数 \(n\) の多項式を表す。さらに次を示せ:
- \(Q_{n+1} = (1 + x^{2}) Q_{n}' - 2(n + 1) x Q_{n}\)
- \(Q_{n+2} + 2(n + 2) x Q_{n+1} + (n + 2)(n + 1)(1 + x^{2})Q_{n} = 0\)
- \((1 + x^{2}) Q_{n}'' - 2nx Q_{n}' + n(n + 1)Q_{n} = 0\)
- \(Q_{n} = (-1)^{n} n!\left\{(n + 1)x^{n} - \dfrac{(n + 1)n(n - 1)}{3!} x^{n-2} + \cdots\right\}\)
- \(Q_{n}\) の根は全て実数で、\(Q_{n-1} = n\) の根によって分断される。
-
\(f(x),\ \phi(x),\ \psi(x)\) が \(a \leq x \leq b\) で導関数を持つなら、\(a\) と \(b\) の間のある \(\xi\) で次が成り立つ: \[ \begin{vmatrix} f(a) & \phi(a) & \psi(a)\\ f(b) & \phi(b) & \psi(b)\\ f'(\xi)& \phi'(\xi)& \psi'(\xi) \end{vmatrix} =0 \] [三行目を \(f(x),\ \phi(x),\ \psi(x)\) に入れ替えて得られる関数を考える。この命題で \(\phi(x) = x,\ \psi(x) = 1\) とすると平均値の定理 (§125) が得られる]
-
問題 32 から次の等式を導け: \[ \frac{f(b) - f(a)}{\phi(b) - \phi(a)} = \frac{f'(\xi)}{\phi'(\xi)} \]
-
\(x \to \infty\) のとき \(\phi'(x) \to a\) なら \(\phi(x)/x \to a\) が成り立ち、\(\phi'(x) \to \infty\) なら \(\phi(x) \to \infty\) が成り立つ。 [\(x_{0} \lt \xi \lt x\) に対する等式 \(\phi(x) - \phi(x_{0}) = (x - x_{0})\phi'(\xi)\) を使う]
-
\(x \to \infty\) のとき \(\phi(x) \to a\) なら、\(\phi'(x)\) は \(0\) 以外の極限に向かわない。
-
\(x \to \infty\) のとき \(\phi(x) + \phi'(x) \to a\) なら、\(\phi(x) \to a\) かつ \(\phi'(x) \to 0\) が成り立つ。
[\(\phi(x) = a + \psi(x)\) とすれば \(\psi(x) + \psi'(x) \to 0\) となる。もし十分大きい \(x\) で \(\psi'(x)\) の符号が一定 (正とする) なら \(\psi(x)\) は単調増加であり、極限 \(l\) または \(\infty\) に向かう。\(\psi(x) \to \infty\) なら \(\psi(x) + \psi'(x) \to 0\) より \(\psi'(x) \to -\infty\) だが、これは \(\phi'(x)\) の符号に関する仮定に反する。\(\psi(x) \to l\) なら \(\phi'(x) \to -l\) だが、これは \(l = 0\) でない限りあり得ない (問題 35)。同様の理由で \(\psi'(x)\) が極限で負になることもない。一方 \(\psi(x)\) の符号が変化し極限が存在しないなら、\(\psi(x)\) には極大値と極小値が存在する。\(\psi(x)\) が極大または極小となる大きい \(x\) では \(\psi(x) + \psi'(x)\) が小さくなり、さらに \(\psi'(x) = 0\) が成り立つ。よって \(\psi(x)\) も小さい。以上より、どんな場合でも \(x\) が大きいときの \(\psi(x)\) は小さいと分かる
この定理の一般化および別証明は拙著 Generalisations of a limit theorem of Mr Mercer, volume 43, Quarterly Journal of Mathematics を参照。上述の単純な証明は E・W・ホブソン教授によって提案された]
-
\(\displaystyle\int R\left\{x, \sqrt{\frac{ax + b}{mx + n}}, \sqrt{\frac{cx + d}{mx + n}}\right\} dx\) を有理関数の積分に帰着させる方法を示せ。[\(mx + n = 1/t\) として 例 49.13 を使う]
-
次の積分を計算せよ: \[ \small \begin{gathered} \int \frac{dx}{(1 + x^{2})^{3}},\quad \int \sqrt{\frac{x - 1}{x + 1}}\, \frac{dx}{x},\quad \int \frac{x\, dx}{\sqrt{1 + x} - \sqrt[3]{1 + x}},\\ \int \sqrt{a^{2} + \sqrt{b^{2} + \frac{c}{x}}}\, dx,\quad \int \cosec^{3}x\, dx,\quad \int \frac{5\cos x + 6}{2\cos x + \sin x + 3}\, dx,\\ \int \frac{dx}{(2 - \sin^{2}x) (2 + \sin x - \sin^{2} x)},\quad \int \frac{\cos x\sin x \, dx}{\cos^{4}x + \sin^{4}x},\quad \int \cosec x \sqrt{\sec 2x}\, dx,\\ \int \frac{dx}{\sqrt{(1 + \sin x) (2 + \sin x)}},\quad \int \frac{x + \sin x}{1 + \cos x}\, dx,\quad \int \text{arcsec } x\, dx,\quad \int (\arcsin x)^{2}\, dx,\\ \int x\arcsin x\, dx,\quad \int \frac{x\arcsin x}{\sqrt{1 - x^{2}}}\, dx,\quad \int \frac{\arcsin x}{x^{3}}\, dx,\quad \int \frac{\arcsin x}{(1 + x)^{2}}\, dx,\\ \int \frac{\arctan x}{x^{2}}\, dx,\quad \int \frac{\arctan x}{(1 + x^{2})^{3/2}}\, dx,\quad \int \frac{\log(\alpha^{2} + \beta^{2}x^{2})}{x^{2}}\, dx,\quad \int \frac{\log(\alpha + \beta x)}{(a + bx)^{2}}\, dx \end{gathered} \]
-
帰着の公式
-
次を示せ: \[ \begin{aligned} & 2(n - 1)(q - \dfrac{1}{4}p^{2}) \int \frac{dx}{(x^{2} + px + q)^{n}} \\ & \qquad = \frac{x + \frac{1}{2}p}{(x^{2} + px + q)^{n-1}} + (2n - 3) \int \frac{dx}{(x^{2} + px + q)^{n-1}} \end{aligned} \]
[\(x + \frac{1}{2}p = t,\ q - \frac{1}{4}p^{2} = \lambda\) とすれば \[ \begin{aligned} \int \frac{dt}{(t^{2} + \lambda)^{n}} & = \frac{1}{\lambda} \int \frac{dt}{(t^{2} + \lambda)^{n-1}} - \frac{1}{\lambda} \int \frac{t^{2}\, dt}{(t^{2} + \lambda)^{n}} \\ & = \frac{1}{\lambda} \int \frac{dt}{(t^{2} + \lambda)^{n-1}} + \frac{1}{2\lambda(n-1)} \int t \frac{d}{dt} \left\{\frac{1}{(t^{2} + \lambda)^{n-1}}\right\} dt \end{aligned} \] を得る。部分積分を使えば示すべき式が求まる。
こういった等式を帰着の公式 (formula of reduction) と呼ぶ。\(n\) が正の整数の場合が一番よく使われる。\(\displaystyle\int \frac{dx}{(x^{2} + px + q)^{n}}\) が \(\displaystyle\int \frac{dx}{(x^{2} + px + q)^{n-1}}\) で表されているので、全ての \(n\) に対する積分を順に求められる]
-
\(I_{p, q} = \displaystyle\int x^{p}(1 + x)^{q}\, dx\) とする。このとき \[ (p + 1) I_{p, q} = x^{p+1}(1 + x)^{q} - qI_{p+1, q-1} \] を示し、\(I_{p, q}\) と \(I_{p-1, 1+1}\) を関連付ける同様の等式を求めよ。さらに置換 \(x = -y(1 + y)\) を使って次の等式を示せ: \[ I_{p, q} = (-1)^{p+1} \int y^{p} (1 + y)^{-p-q-2}\, dy \]
-
\(X = a + bx\) とする。このとき次の等式が成り立つ: \[ \begin{aligned} \int xX^{-1/3}\, dx & = -\frac{3}{10b^{2}}(3a - 2bx) X^{2/3}, \\ \int x^{2}X^{-1/3}\, dx & = \frac{3}{40b^{3}}(9a^{2} - 6abx + 5b^{2}x^{2}) X^{2/3},\\ \int xX^{-1/4}\, dx & = -\frac{4}{21b^{2}}(4a - 3bx) X^{3/4},\\ \int x^{2}X^{-1/4}\, dx & = \frac{4}{231b^{3}}(32a^{2} - 24abx + 21b^{2}x^{2}) X^{3/4} \end{aligned} \]
-
\(I_{m, n} = \displaystyle\int \frac{x^{m}\, dx}{(1 + x^{2})^{n}}\) とする。このとき次の等式が成り立つ: \[ 2(n - 1)I_{m, n} = -x^{m-1} (1 + x^{2})^{-(n-1)} + (m - 1)I_{m-2, n-1} \]
-
\(I_{n} = \displaystyle\int x^{n} \cos\beta x\, dx\) および \(J_{n} = \displaystyle\int x^{n} \sin\beta x\, dx\) とする。このとき次の等式が成り立つ: \[ \begin{gathered} \beta I_{n} = \hphantom{-} x^{n} \sin\beta x - nJ_{n-1},\\ \beta J_{n} = -x^{n} \cos\beta x + nI_{n-1}\hphantom{,} \end{gathered} \]
-
\(I_{n} = \displaystyle\int \cos^{n} x\, dx\) および \(J_{n} = \displaystyle\int \sin^{n} x\, dx\) とする。このとき次の等式が成り立つ: \[ \begin{gathered} nI_{n} = \hphantom{-} \sin x\cos^{n-1} x + (n - 1) I_{n-2},\\ nJ_{n} = - \cos x\sin^{n-1} x + (n - 1) J_{n-2}\hphantom{,} \end{gathered} \]
-
\(I_{n} = \displaystyle\int \tan^{n}x\, dx\) なら \((n - 1)(I_{n} + I_{n-2}) = \tan^{n-1}x\) が成り立つ。
-
\(I_{m, n} = \displaystyle\int \cos^{m}x \sin^{n}x\, dx\) とする。このとき次の等式が成り立つ: \[ \begin{alignedat}{2} (m+n)I_{m, n} & = -& & \cos^{m+1}x \sin^{n-1}x + (n - 1) I_{m, n-2}\\ & = & & \cos^{m-1}x \sin^{n+1}x + (m - 1) I_{m-2, n} \end{alignedat} \]
[仮定から \[ \begin{aligned} (m+1)I_{m, n} & = -\int \sin^{n-1}x \frac{d}{dx} (\cos^{m+1}x)\, dx\\ & = -\cos^{m+1}x \sin^{n-1}x + (n - 1)\int \cos^{m+2}x \sin^{n-2}x\, dx\\ & = -\cos^{m+1}x \sin^{n-1}x + (n - 1)(I_{m, n-2} - I_{m, n}) \end{aligned} \] が分かる。ここから一つ目の等式が得られる]
-
\(I_{m, n} = \displaystyle\int \sin^{m}x \sin nx\, dx\) と \(I_{m-2, n}\) を関連付ける等式を見つけよ。
(Math. Trip. 1897.)
-
\(I_{m, n} = \displaystyle\int x^{m} \cosec^{n}x\, dx\) とする。このとき次の等式が成り立つ: \[ \begin{aligned} (n - 1)(n - 2)I_{m, n} = {} & (n - 2)^{2}I_{m, n-2} + m(m - 1)I_{m-2, n-2}\\ & \quad -x^{m-1} \cosec^{n-1}x \{m\sin x + (n - 2) x\cos x\} \end{aligned} \]
(Math. Trip. 1896.)
-
\(I_{n} = \displaystyle\int (a + b\cos x)^{-n}\, dx\) とする。このとき次の等式が成り立つ: \[ (n - 1)(a^{2} - b^{2}) I_{n} = -b\sin x (a + b\cos x)^{-(n-1)} + (2n - 3)aI_{n-1} - (n - 2)I_{n-2} \]
-
\(I_{n} = \displaystyle\int (a\cos^{2} x + 2h\cos x\sin x + b\sin^{2}x)^{-n}\, dx\) とする。このとき次の等式が成り立つ: \[ 4n(n + 1)(ab - h^{2})I_{n+2} - 2n(2n + 1)(a + b)I_{n+1} + 4n^{2}I_{n} = -\frac{d^{2} I_{n}}{dx^{2}} \]
(Math. Trip. 1898.)
-
\(I_{m, n} = \displaystyle\int x^{m}(\log x)^{n}\, dx\) とする。このとき次の等式が成り立つ: \[ (m + 1)I_{m, n} = x^{m+1}(\log x)^{n} - nI_{m, n-1} \]
-
-
\(n\) を正の整数とする。このとき \(\displaystyle\int x^{m}(\log x)^{n}\, dx\) は次に等しい: \[ x^{m+1} \left\{\frac{(\log x)^{n}}{m + 1} - \frac{n(\log x)^{n-1}}{(m + 1)^{2}} + \frac{n(n - 1)(\log x)^{n-2}}{(m + 1)^{3}} - \cdots + \frac{(-1)^{n}n!}{(m + 1)^{n+1}}\right\} \]
-
全ての \(x\) に対して \(\phi'' + a^{2}\phi = 0\) となる関数 \(\phi(x)\) は一般に \(A\cos ax + B\sin ax\) つまり \(\rho\cos(ax + \varepsilon)\) という形をしている。ここで \(A,\ B,\ \rho,\ \varepsilon\) は定数を表す。 [\(2\phi'\) を両辺に乗じて積分すると、定数 \(b\) に対して \({\phi'}^{2} + a^{2}\phi^{2} = a^{2}b^{2}\) が分かる。ここから \(ax = \displaystyle\int \frac{d\phi}{\sqrt{b^{2} - \phi^{2}}}\) が導かれる]
-
\(y' + \omega z = 0\) かつ \(z' - \omega y = 0\) を満たす最も一般的な関数 \(y\) と \(z\) を求めよ。\(\omega\) は定数で、ダッシュは \(x\) に関する微分を表す。
-
\(\alpha\) を鋭角を表す定数としたとき、曲線 \[ x = \cos\phi + \frac{\sin\alpha \sin\phi}{1 - \cos^{2}\alpha \sin^{2}\phi},\quad y = \sin\phi - \frac{\sin\alpha \cos\phi}{1 - \cos^{2}\alpha \sin^{2}\phi} \] が定める領域の面積は \(\dfrac{1}{2}\dfrac{(1 + \sin\alpha)^{2}}{\sin\alpha}\pi\) である。
(Math. Trip. 1904.)
-
半径 \(a\) の円の弦で直径に射影すると長さが \(2a\cos\beta\) となるものを考える。この弦の中点の軌跡は二つのループからなり、ループの面積がどちらも \(a^{2}(\beta - \cos\beta\sin\beta)\) だと示せ。
(Math. Trip. 1903.)
-
曲線 \((x/a)^{2/3} + (y/b)^{2/3} = 1\) を四等分した部分の長さが \((a^{2} + ab + b^{2})/(a + b)\) だと示せ。
(Math. Trip. 1911.)
-
半径 \(a\) の円の中に点 \(A\) があり、\(A\) は円の中心から \(b\) だけ離れている。\(A\) から円の接線に下ろした垂線の足の軌跡が、面積が \(\pi(a^{2} + \frac{1}{2}b^{2})\) の領域を囲むと示せ。
(Math. Trip. 1909.)
-
\((a, b, c, f, g, h \mathbin{)\kern-5pt(} x, y, 1)^{2} = 0\) が円錐曲線の方程式なら、 \[ \int \frac{dx}{(lx + my + n)(hx + by + f)} = \alpha\log \frac{PT}{PT'} + \beta \] が成り立つ。ここで \(PT,\ PT'\) は円錐曲線上の点 \(P\) から弦 \(lx + my + n = 0\) の端点における接線に下ろした垂線の長さを表し、\(\alpha\) と \(\beta\) は定数とする。
(Math. Trip. 1902.)
-
積分 \[ \int \frac{ax^{2} + 2bx + c}{(Ax^{2} + 2Bx + C)^{2}}\, dx \] が \(x\) の有理関数となるのは \(AC - B^{2}\) と \(aC + cA - 2bB\) のどちらかが \(0\) になる場合に限られることを示せ10。
-
\(f\) と \(F\) が多項式で、\(F\) は重根を持たないとする。このとき \[ \int \frac{f(x)}{\{F(x)\}^{2}}\, dx \] が \(x\) の有理関数となるための必要十分条件は \(f'F' - fF''\) が \(F\) で割り切れることだと示せ。
-
積分 \[ \int \frac{\alpha\cos x + \beta\sin x + \gamma}{(1 - e\cos x)^{2}}\, dx \] が \(\cos x\) と \(\sin x\) の有理関数となるのは \(\alpha e + \gamma = 0\) の場合に限ると示せ。そしてこの条件が成り立つときの積分を計算せよ。
-
接線が \(OX\) と垂直になる例外的な場合は考えていない (後で考える)。この仮定があれば、この二つの疑問文は同値となる。[return]
-
例えばクリスタル著 Algebra, vol. i, pp.151 et seq. がある。[return]
-
連続であるが導関数を持たない関数にも極大および極小となる点が存在する場合がある。この定理ではもちろん導関数の存在を仮定している。[return]
-
\(-1/(\sqrt{p} - \sqrt{q})^{2}\) が極大値で \(-1/(\sqrt{p} + \sqrt{q})^{2}\) が極小値となる。極小値の方が大きい。[return]
-
例えばクリスタル著 Algebra, vol. i, pp. 151–9 を参照。[return]
-
拙著 "The integration of functions of a single variable" (Cambridge Tracts in Mathematics, No. 2, second edition, 1915) を参照。実際の関数でこうなることは少ない。[return]
-
ここで説明した積分方法は \(a/A = b/B\) のときには行えない。しかしこのときは置換 \(ax + b = t\) で積分を簡略化できる。代数関数の積分についてさらに詳しくは Stolz, Grundzüge der Differential-und-integralrechnung, vol. i, pp. 331 et seq. および Bromwich, Elementary Integrals (Bowes and Bowes, 1911) を参照。別の帰着が Sir G. Greenhill によっても示されている: 彼の A Chapter in the Integral Calculus, pp. 12 et seq. および §131 で示した文献を参照。[return]