§23 多項式
これからの例を見れば、無限に存在する様々な種類の関数をよりよく理解できるだろう。
-
多項式: 次の形をした関数を \(x\) の多項式 (polynomial) と呼ぶ: \[ a_{0}x^{m} + a_{1}x^{m-1} + \cdots + a_{m} \] ここで \(a_{0},\ a_{1},\ \ldots,\ a_{m}\) は定数を表す。もっとも単純な多項式は \(x\) のべき乗 \(y = x,\ x^{2},\ x^{3},\ \ldots,\ x^{m},\ \ldots\) であり、\(x^{m}\) のグラフは \(m\) の偶奇によって二つに分かれる。
まず \(m = 2\) の場合を考える。このとき三つの点 \((0, 0),\ (1, 1),\ (-1, 1)\) はグラフ上にある。グラフ上のその他の点は \(x\) に特定の値を代入すれば得られる。例えば \[ x = \frac{1}{2},\quad 2,\quad 3,\quad -\frac{1}{2},\quad -2,\quad 3 \quad \] のとき、それぞれ \[ y = \frac{1}{4},\quad 4,\quad 9,\quad \hphantom{-}\frac{1}{4},\quad \hphantom{-}4,\quad 9 \quad \] となる。グラフ上の点をいくつかプロットすれば、グラフ全体が 図 8 のような形をしていると予想できる。グラフ上にあると分かった点を結んで曲線を描き、適当な別の \(x\) とそれに対応する \(y\) をプロットしてその正確さをテストすれば、新しい点が曲線にとても近いことが分かるだろう (手で書いた分だけ不正確にはなる)。この曲線はもちろん放物線である。
しかしここで、現段階では正確に答えられない重要な問題が一つある。読者も聞いたことがあるであろう連続曲線 (continuous couve) という言葉についてである。連続曲線と言えば値が飛んだりしない繋がった曲線のことであり、例えば 図 8 にある曲線は連続曲線に見える。問題は、関数 \(y = x^{2}\) のこのグラフが本当に連続曲線かどうかである。曲線上の点を個別にたくさん計算すれば見た目は連続らしく見えるが、これは証明ではない。
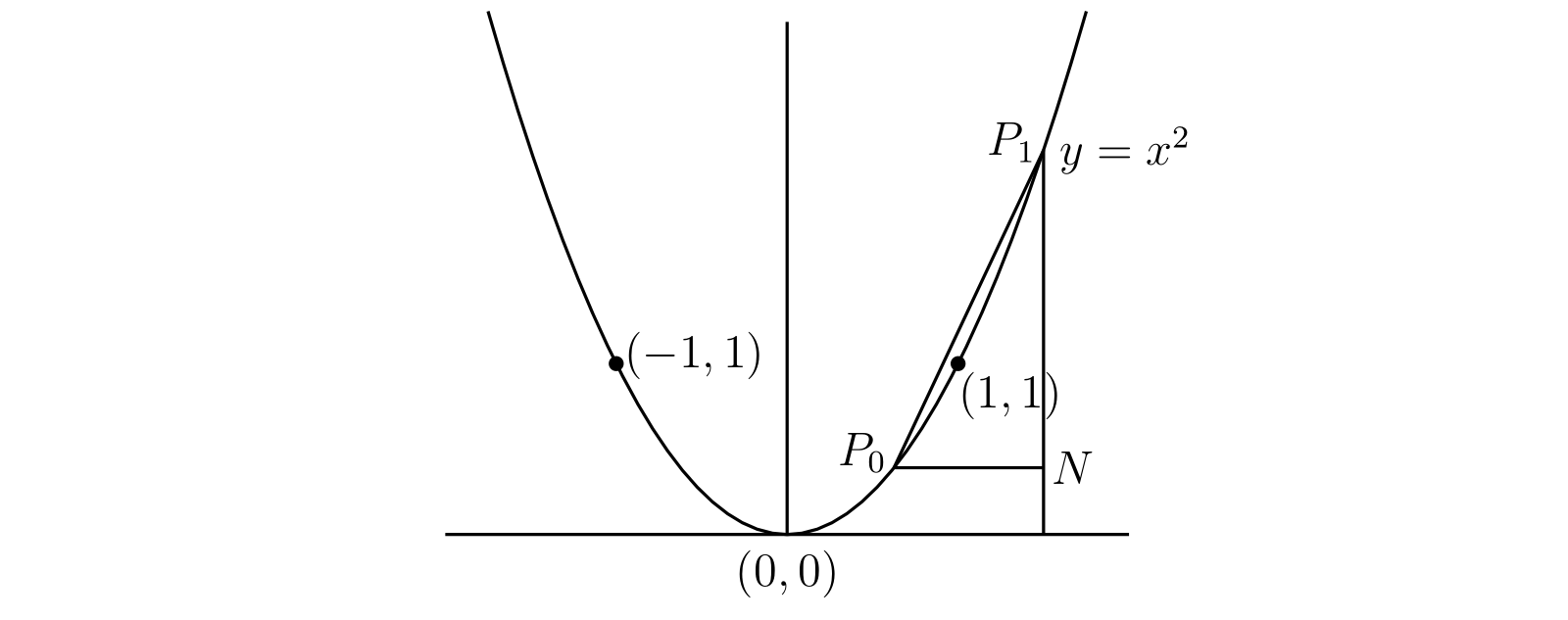 図 8
図 8この問題は第五章まで議論できない。第五章では私たちが普通に使う「連続」という言葉の正確な意味を正確に議論し、上述のグラフおよびこの章でこれから考えるいくつかのグラフが確かに連続なことを証明する。なので今のところは、関数のグラフを「常識的に」描いてもらって構わない。
\(y = x^{2}\) が いたるところで \(x\) 軸に対して凸なことは簡単に示せる。\(P_{0},\ P_{1}\) を \((x_{0}, x_{0}^{2}),\ (x_{1}, x_{1}^{2})\) とする (図 8 参照)。このとき弦 \(P_{0}P_{1}\) 上にある点の座標は、和が \(1\) である二つの正の実数 \(\lambda\) と \(\mu\) を使って \(x = \lambda x_{0} + \mu x_{1},\ y = \lambda x_{0}^{2} + \mu x_{1}^{2}\) と表せる。さらに \[ \begin{aligned} y - x^{2} & = (\lambda + \mu)(\lambda x_{0}^{2} + \mu x_{1}^{2}) - (\lambda x_{0} + \mu x_{1} )^{2} \\ & = \lambda\mu(x_{1} - x_{0})^{2} \geq 0 \end{aligned} \] が成り立つから、この弦は完全に曲線の上にある。
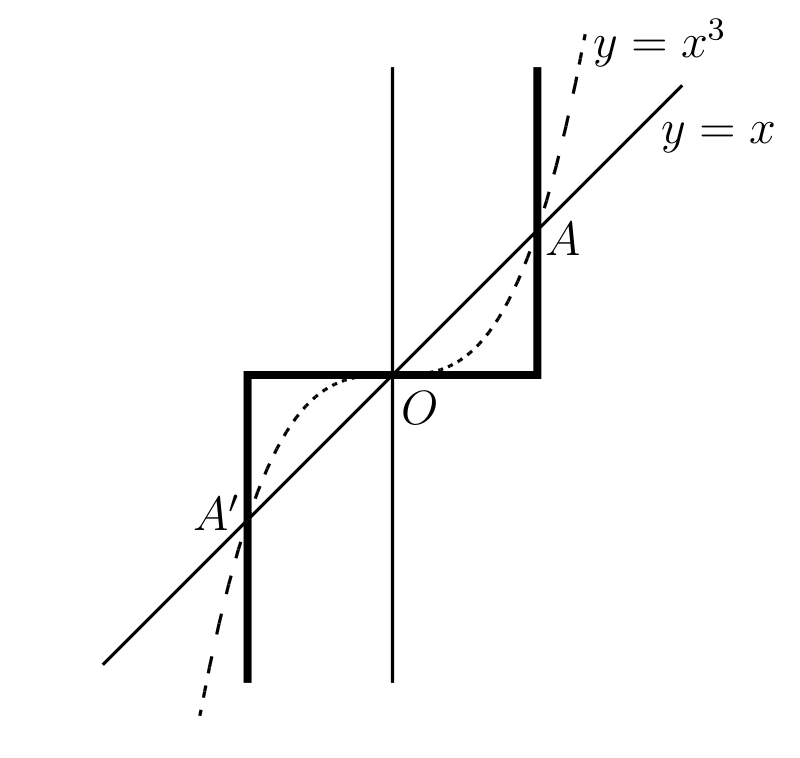
曲線 \(y = x^{4}\) は全体的に \(y = x^{2}\) と似ているが、\(O\) の近くではより緩やかであり、図 9 中の \(A,\ A'\) を超えるとより急になる。そして \(4\) より大きい偶数 \(m\) に対してはこの性質がさらに顕著になる。\(m\) が大きくなると緩やかな部分と急な部分がさらに強調され、最終的に見た目では図中の太い線と区別できなくなる。
次に奇数 \(m\) に対する \(y = x^{m}\) のグラフを考える。二つのグラフの重要な違いは、\(m\) が偶数のときは \((-x)^{m} = x^{m}\) なのでグラフが \(OY\) に関して対称となるのに対して、\(m\) が奇数のときは \((-x)^{m} = -x^{m}\) なので \(x\) が負のとき \(y\) が負となる点にある。図 10 に曲線 \(y = x\) と \(y = x^{3}\) を示す。太線は大きな奇数の \(m\) に対する \(y = x^{m}\) を近似した曲線である。
ここまでくれば、任意の多項式のグラフを (いくらか理論的に) 描くことができる。まず \(y = x^{m}\) のグラフがあれば、全ての点の縦座標を \(C\) 倍することで \(y = Cx^{m}\) のグラフが得られる (\(C\) は整数)。次にもし \(f(x)\) と \(F(x)\) のグラフがあれば、全ての点に対して二つのグラフの縦座標の和をとることで \(f(x) + F(x)\) のグラフが得られる。
しかし多項式のグラフの描画にはもっと簡単な微積分を使った方法がある。この方法は後で説明するので、この話題はここまでとする。
-
曲線 \(y = 7x^{4},\ y = 3x^{5},\ y = x^{10}\) の通る点を調べよ。
[三つのグラフは一つの図に注意深く描くこと1。\(x\) の項が持つ最大の指数が大きいと、\(x\) が大きくなるにしたがって値が急速に大きくなることが分かるだろう。また \[ x^{10} + 3x^{5} + 7x^{4} \] といった多項式では (あるいは \(x^{10} + 30x^{5} + 700x^{4}\) でさえ)、\(x\) が大きいときに大部分を占めるのは最初の項である。\(x = 4\) のときでさえ \(x^{10} \gt 1,000,000\) であり、このとき \(30x^{5} \lt 35,000\) および \(700x^{4} \lt 180,000\) に過ぎない。\(x = 10\) ともなれば最初の項はさらに大きくなる]
-
\(x = 1,\ 10,\ 100\) といった値で \(x^{12},\ 1,000,000x^{6},\ 1000,000,000,000x\) の相対的な大きさを比較せよ。
[同じような例を他にも作ってみるとよい。関数の相対的な増加速度という考え方はこれから何度も出てくる]
-
\(ax^{2} + 2bx + c\) のグラフを描け。
[\(y - \{(ac - b^{2})/a\} = a\{x + (b/a)\}^{2}\) だから、点 \((-b/a, (ac - b^{2})/a)\) を通る新しい軸を元の軸と平行に取れば、この方程式は新しい軸における \(y' = a{x'}^{2}\) となる。この曲線は放物線である]
-
曲線 \(y = x^{3} - 3x + 1,\ y = x^{2}(x - 1),\ y = x(x - 1)^{2}\) が通る点を調べよ。
-
\(y\) 軸方向の目盛りを \(x\) 軸方向の目盛りより小さく描いた方がよい。そうしないと図がとてつもない大きさになる[return]