§9 実数の大きさの関係

数の概念を拡張して次に当然行うべきは、対応する等号・不等号・加算・乗算といった概念の拡張である。こういった概念を新しい数に適用する方法、そして拡張された概念が通常の代数法則を満たすことを示す必要がある。この証明がなくては、一般的な実数を §1 の有理数と同じように扱えない。しかし全てを詳細に示すには多くの紙面が必要になるので、ここでは詳細な議論の進め方を大まかに示すに留める。

実数は \(\alpha,\ \beta,\ \gamma,\ \ldots\) といったギリシャ文字で表し、対応する下のクラスと上のクラスに属する有理数をそれぞれ \(a\) と \(A\)、\(b\) と \(B\)、\(c\) と \(C\) と言ったアルファベットで表す。クラス自身は \((a),\ (A)\) などで表す。

二つの実数 \(\alpha\) と \(\beta\) の関係には三つの可能性がある:

1. 全ての \(a\) が \(b\) であり、全ての \(A\) が \(B\) である。このとき \((a)\) と \((b)\) および \((A)\) と \((B)\) は同一となる。
2. 全ての \(a\) は \(b\) であるが、\(A\) の全ては \(B\) でない。このとき \((a)\) は \((b)\) の真の部分¹となり、かつ \((B)\) は \((A)\) の真の部分となる。
3. 全ての \(A\) は \(B\) だが、\(a\) の全ては \(b\) でない。

この三つの場合を 図 4 に図示する。

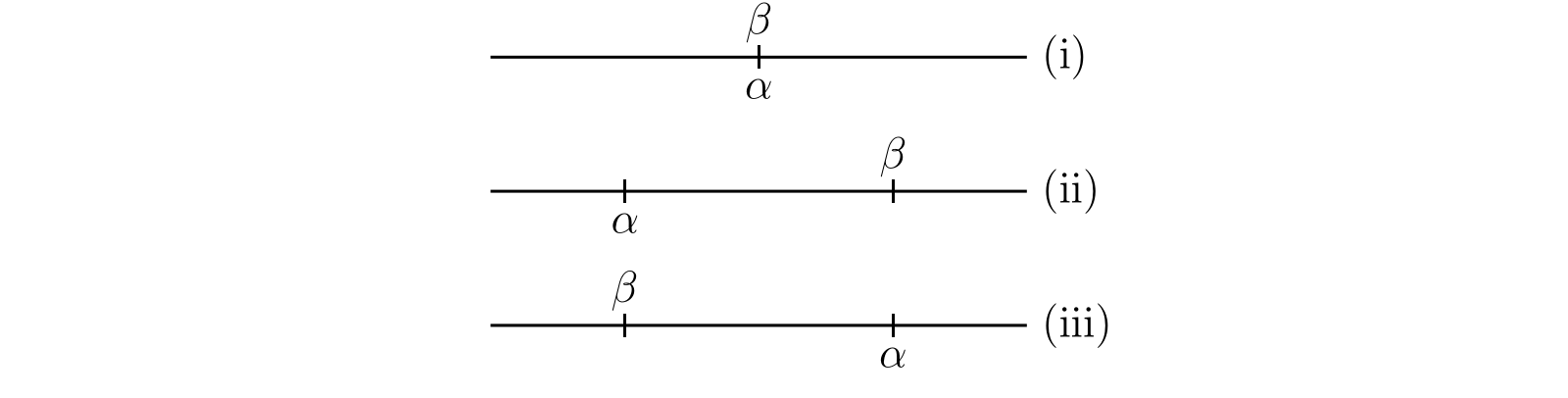
(i) のとき \(\alpha = \beta\) と表記し、(ii) のときは \(\alpha \lt \beta\) と、(iii) のときは \(\alpha \gt \beta\) と表記する。\(\alpha\) と \(\beta\) が共に有理数のとき、私たちが知っているとみなしていた有理数に関する等式と不等式がこの定義と矛盾しないことは明らかである。また任意の正の数が任意の負の数より大きいことも容易に分かる。

この段階で正の数 \(\alpha\) に対する負の数 \(-\alpha\) 定義すると便利だろう。\((a),\ (A)\) を \(\alpha\) に対応するクラスとして、下のクラスに全ての \(-A\) を、上のクラスに全ての \(-a\) を取ると新たな切断を定義できる。こうして定義される実数を \(-\alpha\) と表す。\(-\alpha\) は明らかに負となる。同様に \(\alpha\) が負または \(0\) のときにも \(-\alpha\) を定義できる。\(\alpha\) が負ならば \(-\alpha\) は正となり、\(-(-\alpha) = \alpha\) なことは容易に分かる。\(\alpha\) と \(-\alpha\) のうち一方が正となる (\(\alpha = 0\) の場合は除く) が、二つのうち正の方を \(|\alpha|\) と表記し、\(\alpha\) の絶対値 (absolute value) あるいは大きさ (modulus) と呼ぶ。

[以上の結果は全て定義から直ちに得られる]

1. つまり \((a)\) は \((b)\) に含まれ、かつ \((b)\) と同じではない。^[return]