§28 超越関数

\(\cos x,\ \sin x\) および \(a\cos x + b\sin x\) のグラフを描け。

[サインとコサインがそれぞれ \(a/\sqrt{a^{2} + b^{2}}\) と \(b/\sqrt{a^{2} + b^{2}}\) である値を \(\alpha\) とし、さらに \(\beta = \sqrt{a^{2} + b^{2}}\) とすれば、\(a\cos x + b\sin x = \beta\cos(x - \alpha)\) が成り立つ。そのため三つの関数のグラフは相似である]

\(\cos^{2} x,\ \sin^{2} x,\ a\cos^{2} x + b\sin^{2} x\) のグラフを描け。

\(f(x)\) と \(F(x)\) のグラフが描かれているとする。このとき \[ f(x)\cos^{2} x + F(x)\sin^{2} x \] のグラフは \(y = f(x)\) と \(y = F(x)\) の間を揺れ動く曲線となる。\(f(x) = x,\ F(x) = x^{2}\) のときのグラフを描け。

\(\cos px + \cos qx\) のグラフが \(2\cos\frac{1}{2}(p - q)x\) と \(-2\cos\frac{1}{2}(p + q)x\) のグラフの間にあり、二つのグラフに交互に接することを示せ。\((p - q)/(p + q)\) が小さい場合のグラフの概形を描け。

(Math. Trip. 1908.)

\(x + \sin x,\ \ \dfrac{1}{x} + \sin x,\ \ x\sin x,\ \ \dfrac{\sin x}{x}\) のグラフを描け。

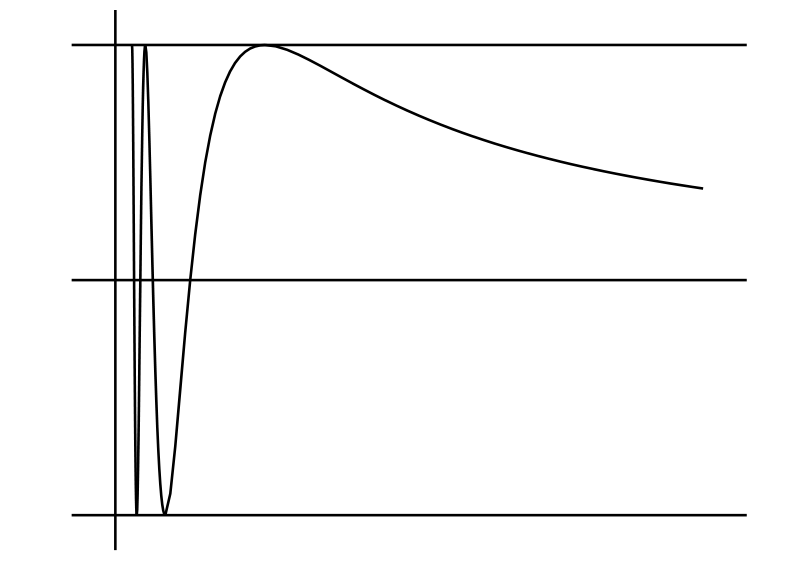
\(\sin\dfrac{1}{x}\) のグラフを描け。 [\(y = \sin(1/x)\) とすると任意の整数 \(m\) に対して \(x = 1/m\pi\) で \(y = 0\) となる。同様に \(x = 1/(2m + \frac{1}{2})\pi\) なら \(y = 1\)、\(x = 1/(2m - \frac{1}{2})\pi\) なら \(y = -1\) である。この曲線は全体が \(y = -1\) と \(y = 1\) の間に収まる (図 13)。グラフは上下に振動し、そのスピードは \(x\) が \(0\) に近づくにつれて速くなる。\(x = 0\) では関数が定義されない。また \(x\) が大きいとき \(y\) は小さくなる²。曲線の負の部分は正の部分と相似である]

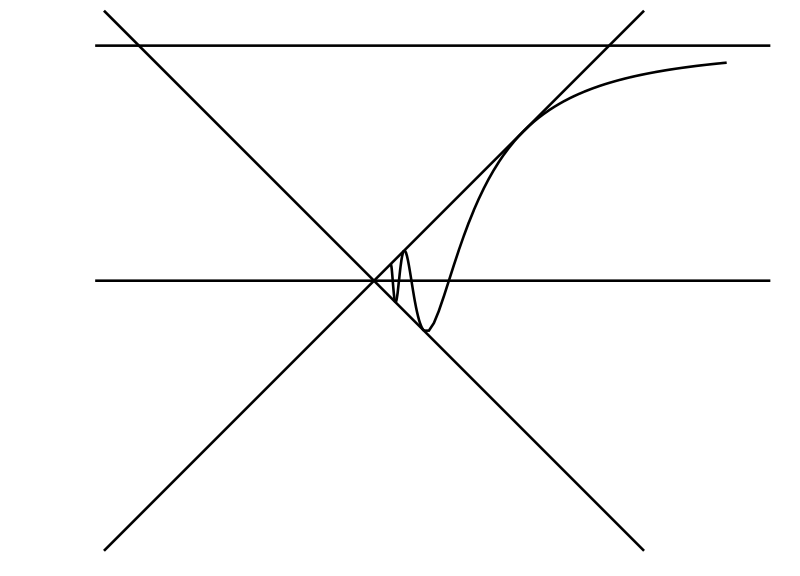
\(x\sin\dfrac{1}{x}\) のグラフを描け。

[前問の曲線が \(y = -1\) と \(y = 1\) の間にあったのと同様に、この曲線は \(y = -x\) と \(y = x\) の間にある (図 14)]

次の関数のグラフを描け: \[ x^{2}\sin \frac{1}{x},\quad \frac{1}{x}\sin \frac{1}{x},\quad \sin^{2} \frac{1}{x},\quad \left\{x\sin \frac{1}{x}\right\}^{2}, \] \[ \quad a\cos^{2} \frac{1}{x} + b\sin^{2} \frac{1}{x}, \quad \sin x + \sin \frac{1}{x},\quad \sin x\sin \frac{1}{x} \]

次の関数のグラフを描け: \[ \cos x^{2},\ \sin x^{2},\ a\cos x^{2} + b\sin x^{2} \]

\(\arccos x\) と \(\arcsin x\) のグラフを描け。

[\(y = \arccos x\) なら \(x = \cos y\) が成り立つ。この関係から、\(y\) の関数 \(x = \cos y\) のグラフから \(x\) の関数 \(y = \arccos x\) のグラフが得られると分かる。明らかに \(y\) は \(-1 \leq x \leq 1\) でのみ定義され、この \(x\) に対して無限個の値を持つ。つまり \(-1 \lt x \lt 1\) に対する \(0\) と \(\pi\) の間の \(y\) の値を \(\alpha\) すれば、他の \(y\) の値は \(n\) を (正負を問わない) 任意の整数として \(2n\pi ± \alpha\) となる]

次のグラフを描け: \[ \tan x,\quad \cot x,\quad \sec x, \quad \cosec x,\quad \tan^{2} x,\quad \cot^{2} x, \quad \sec^{2} x,\quad \cosec^{2} x \]

\(\arctan x,\ \operatorname{arccot} x,\ \operatorname{arcsec} x,\ \operatorname{arccosec} x\) のグラフを描け。特定の一つの値から他の関数の全ての値を表す (問題 10 で示したような) 式を示せ。

\(\tan \dfrac{1}{x},\ \cot \dfrac{1}{x},\ \sec \dfrac{1}{x},\ \cosec \dfrac{1}{x}\) のグラフを描け。

\(\cos x\) と \(\sin x\) が \(x\) の有理関数でないことを示せ。

[\(f(x)\) が定義される全ての \(x\) に対して \(f(x) = f(x + a)\) が成り立つとき、関数 \(f\) は周期的 (perdiodic) であると言い、\(a\) をその周期 (period) と呼ぶ。\(\cos x\) と \(\sin x\) は周期 \(2\pi\) の周期関数である。定数でない有理関数が周期関数でないことは次の通り簡単に示せる。\(P\) と \(Q\) が多項式で \[ f(x) = \frac{P(x)}{Q(x)} \] と仮定し、全ての \(x\) で \(f(x) = f(x + a)\) とする。\(f(0) = k\) と置くと、方程式 \(P(x) - kQ(x) = 0\) は \(x = 0,\ a,\ 2a,\ \ldots\) という無限に多くの \(x\) で満たされる。したがってこの方程式は全ての \(x\) で成り立ち、\(f(x) = k\) すなわち \(f(x)\) は定数である]

より一般的に、周期を持つ関数は \(x\) の代数関数でないことを示せ。

[代数関数を定義する方程式を \[ y^{m} + R_{1}y^{m-1} + \cdots + R_{m} = 0 \qquad \text{(1)} \] とする。ここで \(R_{1},\ \ldots\ \) は \(x\) の有理関数である。これを変形すると、\(x\) の多項式 \(P_{0},\ P_{1},\ \ldots\ \) を使って \[ P_{0}y^{m} + P_{1}y^{m-1} + \cdots + P_{m} = 0, \] となる。前問と同様の議論により \[ P_{0}k^{m} + P_{1}k^{m-1} + \cdots + P_{m} = 0 \] が全ての \(x\) について成り立つ。よって \(y = k\) とすれば (1) が全ての \(x\) について満たされる。すなわち今考えている代数関数の値の一つは定数に単純化される。

さらに (1) を \(y - k\) で割って同じ議論を繰り返す。すると私たちが考えている代数関数は全ての \(x\) について \(k,\ k',\ \ldots\) という定数値しかとらない、つまりこの関数はいくつかの定数値からなることが最終的に結論できる]

サインとコサインの逆関数は有理関数でも代数関数でもない。 [\(-1\) と \(1\) の間の任意の \(x\) に対する \(\arcsin x\) と \(\arccos x\) の値が無限個あることから示せる]