§29 その他の超越関数
-
三角関数に次いで重要なのが、指数関数と対数関数である。これらの関数は第九章と第十章で取り上げるが、今の私たちには手に余る。また性質が調べられているその他の超越関数、例えば楕円関数・ベッセル関数・ラグランジュ関数・ガンマ関数はどれもこの本の範囲を超える。しかし初等的な関数の中には、理論的な重要性が有理関数・代数関数・三角関数よりも劣るものの、グラフを描くことで関数的な関係の可能性をよりよく理解できるものが存在する。
-
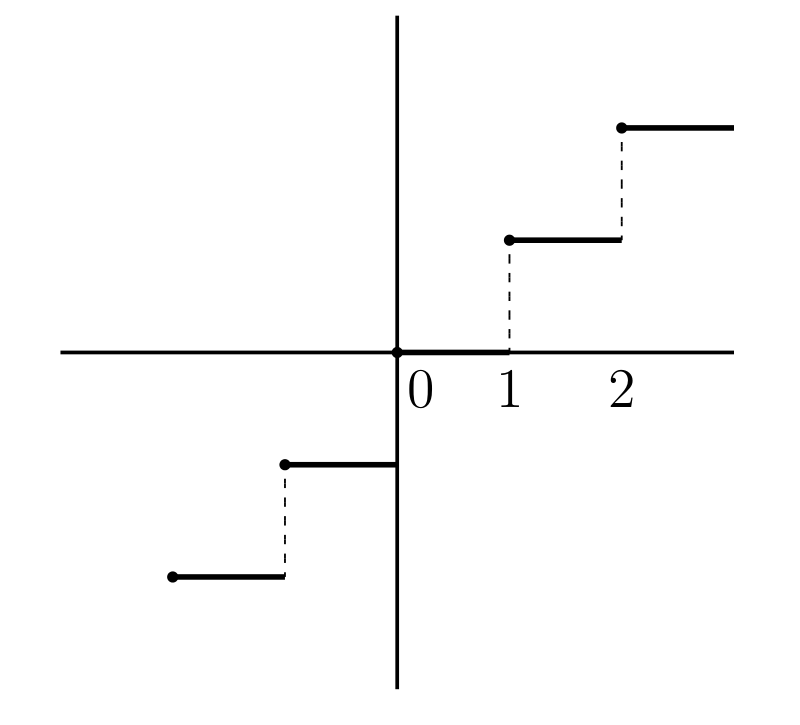
\(x\) を越えない最大の整数を \([x]\) で表すとする。\(y = [x]\) のグラフを 図 15a に示す。太線の左端の点はグラフに含まれるが、右端の点は含まれない。
-
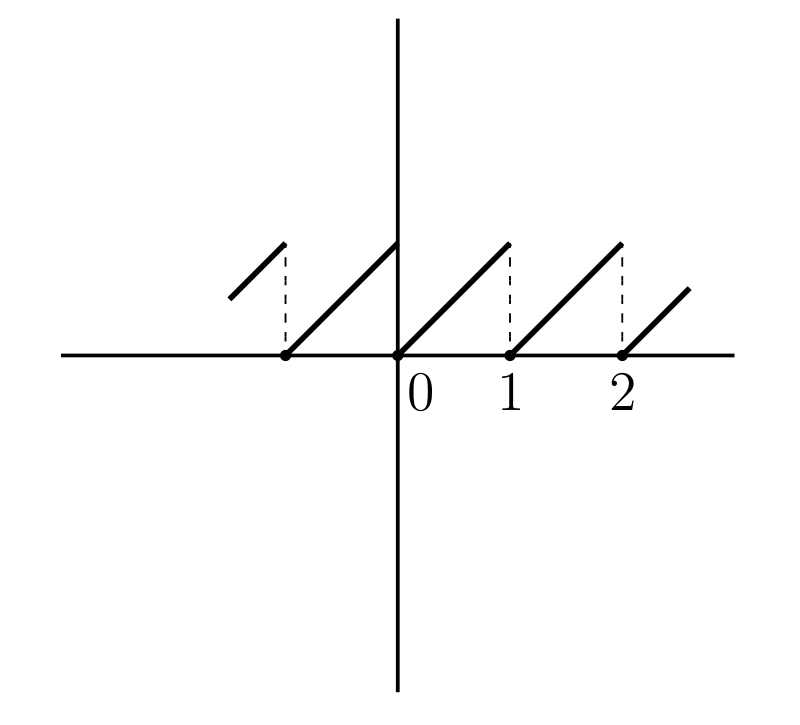
\(y = x - [x]\) (図 15b)
-
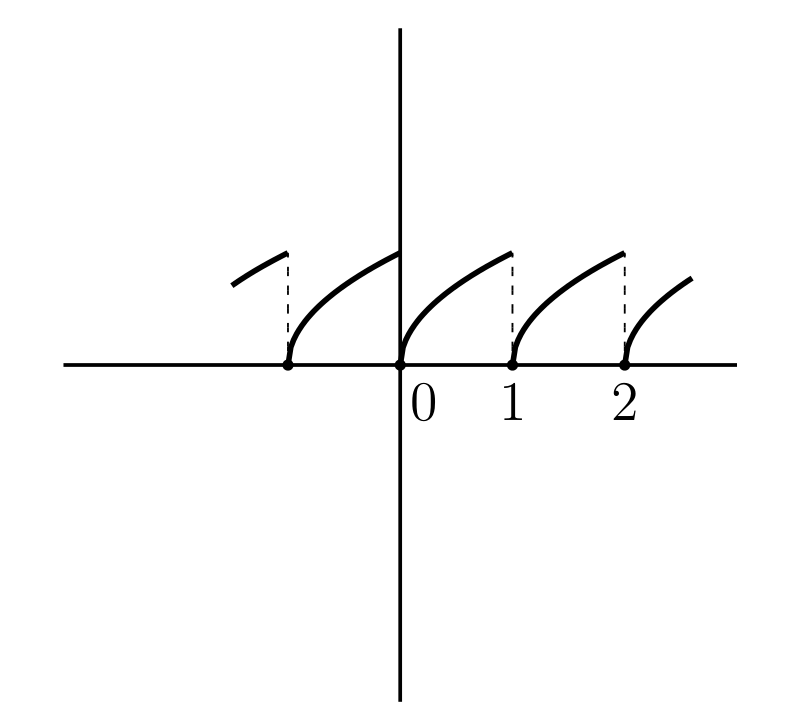
\(y = \sqrt{x - [x]}\) (図 15c)
-
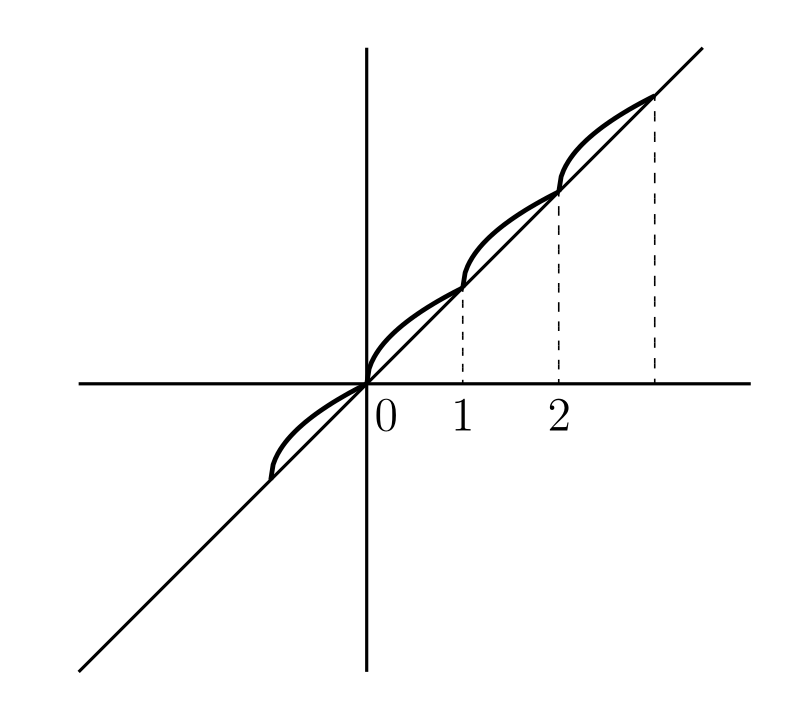
\(y = [x] + \sqrt{x - [x]}\) (図 15d)
-
\(y = (x - [x])^{2},\ y = [x] + (x - [x])^{2}\)
-
\(y = [\sqrt{x}],\ y = [x^{2}],\ y = \sqrt{x} - [\sqrt{x}],\ y = x^{2} - [x^{2}],\ y = [1 - x^{2}]\)
-
\(y\) を \(\bm{x}\) の最大素因数と定義する (例 10.6)。このとき \(y\) は整数の \(x\) に対してのみ定義される。もし \[ x = 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9,\ 10,\ 11,\ 12,\ 13,\ \ldots, \] なら \[ y = 1,\ 2,\ 3,\ 2,\ 5,\ 3,\ 7,\ 2,\ 3,\ \hphantom{1} 5,\ 11,\ \hphantom{1} 3,\ 13,\ \ldots\hphantom{,} \] であり、グラフは孤立した点から構成される。
-
\(y\) を \(\bm{x}\) の分母とする (例 10.7)。すると \(y\) は有理数の \(x\) に対してしか定義されない。グラフ上の点は好きなだけ多くプロットできるが、最終的なグラフは通常の意味での曲線ではない。無理数 \(x\) に対応する点が存在しない。
\(N\) を正の整数として、点 \((N - 1, N)\) と \((N, N)\) を結ぶ直線を引く。この直線上にある点の個数が \(N\) と互いに素な \(N\) より小さい正の整数の数と等しいことを示せ。
-
\(x\) が整数のとき \(y = 0\) で、\(x\) が整数でないとき \(y = x\) と定める。この関数のグラフは直線 \(y = x\) から \[ \ldots, \quad (-1, -1),\quad (0, 0),\quad (1, 1),\quad (2, 2),\quad \ldots \] という点を取り除き、\(x\) 軸上の \(\ldots,\ (-1, 0),\ (0, 0),\ (1, 0),\ \ldots\ \) という点を追加したものになる。
この関数は道理にかなっていないと読者は思うかもしれない。「整数でない \(x\) で \(y\) が \(x\) と等しいなら、整数でも \(y = x\) ではないか」と疑問に思うことだろう。この疑問に対する答えは「そうなるべき理由などない」である。実際のところこの \(y\) は関数の定義の本質をよく表していると言える: \(x\) と \(y\) の関係であって \(x\) が分かったときに \(y\) が分かるものであれば、それは関数となる。私たちには好きなようにこの関係を考える自由があり、それがどんなに人為的で荒唐無稽に見えても構わない。もちろんこの関数 \(y\) は、\(x\) が整数を含んだどんな値でも常に \(x\) に等しい関数とは全く異なる。
-
\(x\) が有理数のとき \(y = 1\) で、\(x\) が無理数のとき \(y = 0\) とする。この関数のグラフは \(y = 1\) と \(y = 0\) に並んだ二つの点列からなる。見た目では二つの連続な直線があるように見えるが、実際には抜けている点が両方の直線にそれぞれ無限個ある。
-
\(x\) が無理数のとき \(y = x\) で、\(x\) が有理数 \(p/q\) のとき \(y = \sqrt{(1 + p^{2})/(1 + q^{2})}\) とする。
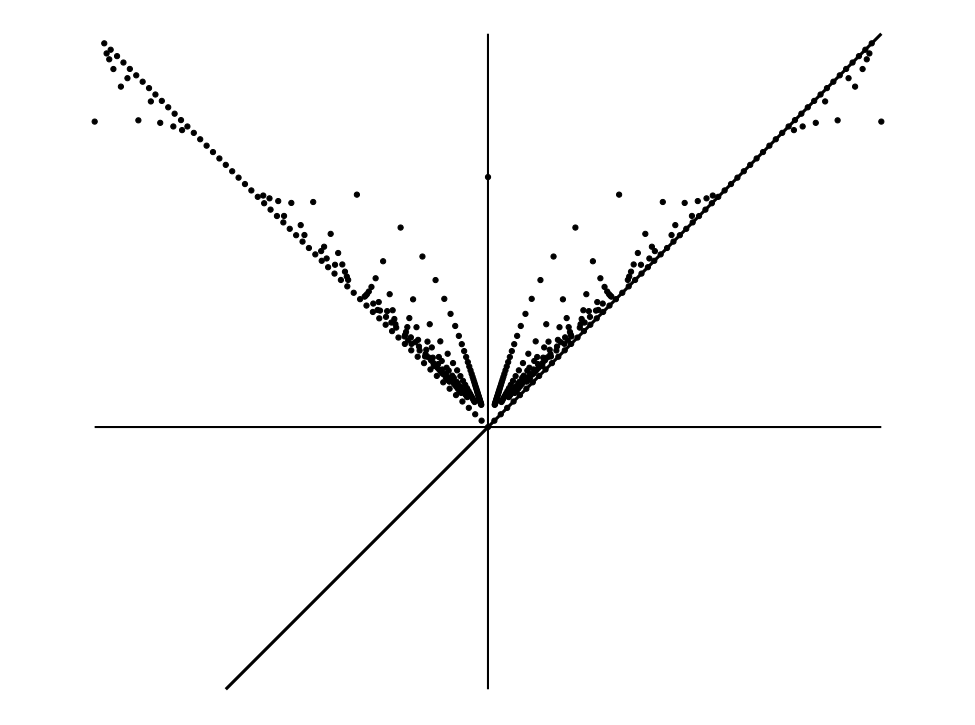 図 16
図 16この関数のグラフの無理数 \(x\) に対応する部分は本当は連続でないが、見た目では直線 \(y = x\) と区別が付かない。
有理数 \(x\) を考える。\(x\) が正なら、\(\sqrt{(1 + p^{2})/(1 + q^{2})}\) が \(p/q\) と等しくなるのは \(p = q\) すなわち \(x = 1\) のときだけである。つまり有理数 \(x\) に対応する \((1, 1)\) 以外の点は全て \(y = x\) から外れる。もし \(p \lt q\) なら \(\sqrt{(1 + p^{2})/(1 + q^{2})} \gt p/q\) が成り立ち、\(p \gt q\) なら \(\sqrt{(1 + p^{2})/(1 + q^{2})} \lt p/q\) が成り立つ。よって \(0 \lt x \lt 1\) なら点は \(y = x\) の上方にあり、\(1 \lt x\) なら下方にある。また \(p\) と \(q\) が大きいと \(\sqrt{(1 + p^{2})/(1 + q^{2})}\) はほぼ \(p/q\) に等しくなり、任意の有理数 \(x\) に対しては任意に大きい分母と分子を持った表現が存在するので、グラフの \(y = x\) の近くには大量の点が集まる。正の \(x\) に対するグラフの概形は直線とその周りに集まる孤立した点の集合からなり、点は直線に近づくほど濃くなる。
負の \(x\) に対応するグラフは、孤立した点を \(y\) 軸に関して対称にした点と不連続な \(y = x\) の残りの部分からなる。そのため \(y\) 軸より左側の点は \(y = x\) の周りではなく \(y = -x\) の周りに集まる。しかし \(y = -x\) はグラフに含まれない (図 16)。