§36 変位の加算
次の式にはまだ意味が与えられていない: \[ \overline{PQ} + \overline{P'Q'},\quad [x, y] + [x', y'] \] 常識的に考えて、二つの変位の和はそれらを連続して適用したときの結果を表す変位として定義される必要がある。\(P'Q'\) と長さが同じで平行な \(QQ_{1}\) を書く。\(P\) に対して \(\overline{PQ}\) と \(\overline{P'Q'}\) を連続して適用すると、\(P\) はまず \(Q\) に移動しその後 \(Q_{1}\) に移動する。よって \(\overline{PQ}\) と \(\overline{P'Q'}\) の和は \(\overline{PQ_{1}}\) として定義するべきと分かる。\(PQ\) と長さが同じで平行な \(OA\)、および \(P'Q'\) と長さが同じで平行な \(OB\) を書いて平行四辺形 \(OACB\) を完成させれば、次が成り立つ: \[ \overline{PQ} + \overline{P'Q'} = \overline{PQ_{1}} = \overline{OA} + \overline{OB} = \overline{OC} \]
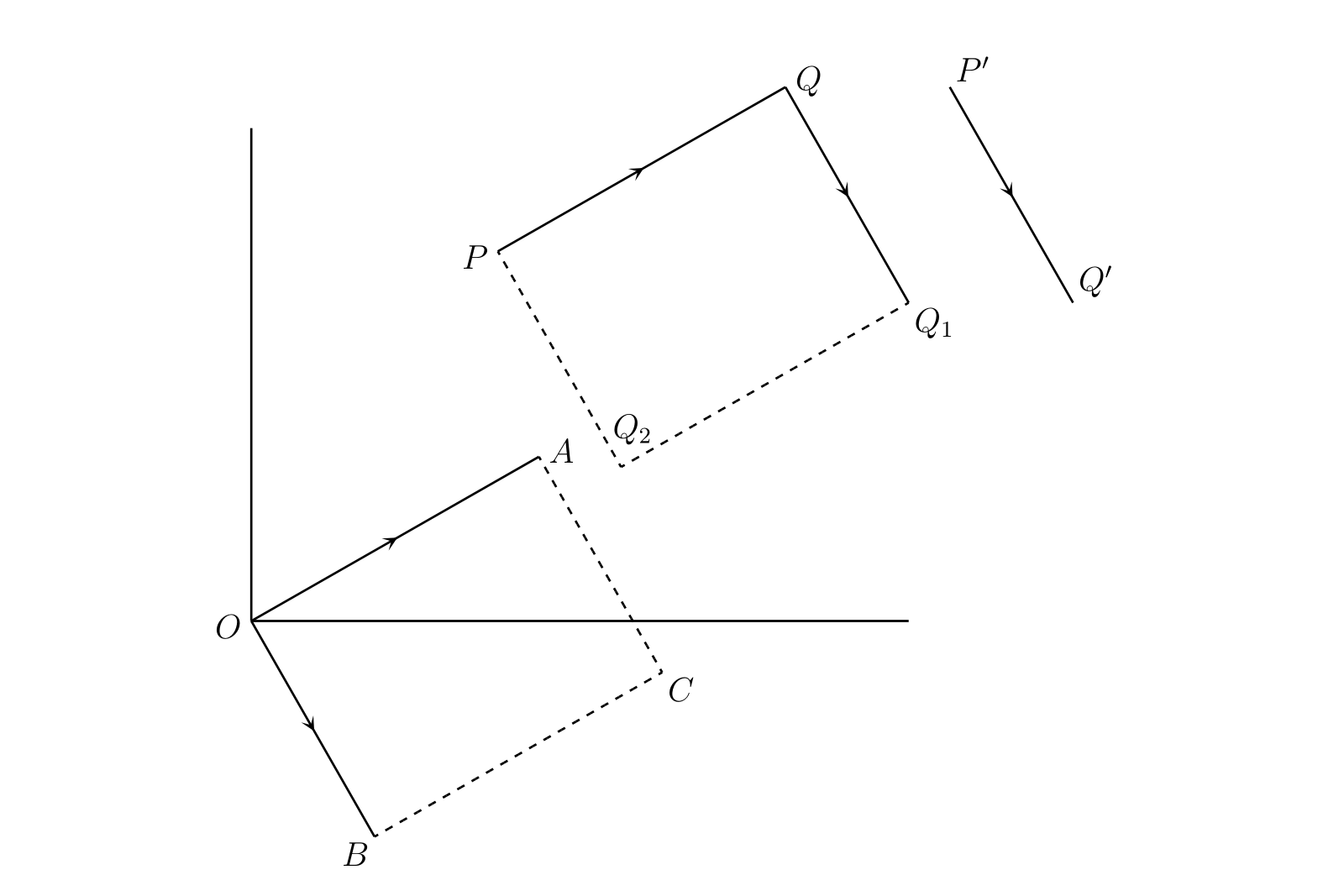
この定義から導かれることを考える。\(B\) の座標が \(x', y'\) なら、\(AB\) の中点の座標は \((\frac{1}{2}(x + x'),\ \frac{1}{2} (y + y'))\)、\(C\) の座標は \((x + x',\ y + y')\) となる。よって \[ [x, y] + [x', y'] = [x + x', y + y'] \qquad \text{(3)} \] が成り立つ。これは変位の和の記号による定義ともみなせる。さらに \[ \begin{aligned} [x', y'] + [x, y] & = [x' + x, y' + y] \\ & = [x + x', y + y'] \\ & = [x, y] + [x', y'] \end{aligned} \qquad \text{(4)} \] も成り立つ。つまり通常の代数における等式 \(a + b = b + a\) と同様に変位の和は交換法則を満たす。\(P\) を最初に \(P'Q'\) と同じ方向と長さだけ移動させ、それから \(PQ\) と同じ方向と長さだけ移動させた場合にも \(P\) が \(Q_{1}\) に到達するというのは幾何学的に明らかであり、変位の交換法則がこの事実を表していると言える。
変位の減算を次のように定義する: \[ [x, y] - [x', y'] = [x, y] + (-[x', y']) \qquad \text{(5)} \] これは \([x, y] + [-x', -y']\) および \([x - x', y - y']\) と同じことである。特に次が成り立つ: \[ [x, y] - [x, y] = [0, 0] \]
変位 \([0, 0]\) は粒子を移動させない。これはゼロ変位 (zero displacement) であり、\([0, 0] = 0\) と表記する。
-
次の等式を示せ:
- \(\alpha [\beta x, \beta y] = \beta [\alpha x, \alpha y] = [\alpha \beta x, \alpha \beta y]\)
- \(([x, y] + [x', y']) + [x'', y''] = [x, y] + ([x', y'] + [x'', y''])\)
- \([x, y] + [x', y'] = [x', y'] + [x, y]\)
- \((\alpha + \beta) [x, y] = \alpha [x, y] + \beta [x, y]\)
- \(\alpha \{[x, y] + [x', y']\} = \alpha [x, y] + \alpha [x', y']\)
[(iii) は前に示した。他の等式も定義から容易に従う。(iii) に対して行ったような幾何学的な意味の考察をそれぞれのケースについて行うこと]
-
\(M\) が \(PQ\) の中点なら \(\overline{OM} = \frac{1}{2}(\overline{OP} + \overline{OQ})\) が成り立つ。一般的に言えば、\(M\) が \(PQ\) を \(\mu : \lambda\) の比に分割するとき、次の式が成り立つ: \[ \overline{OM} = \frac{\lambda}{\lambda + \mu}\, \overline{OP} + \frac{\mu}{\lambda + \mu}\, \overline{OQ} \]
-
\(G\) が同一の粒子 \(P_{1},\ P_{2},\ \ldots,\ P_{n}\) の重心なら、次の式が成り立つ: \[ \overline{OG} = \frac{\overline{OP_{1}} + \overline{OP_{2}} + \cdots + \overline{OP_{n}}}{n} \]
-
\(P,\ Q,\ R\) を同一直線上にある点とすると、\(0\) でない実数 \(\alpha,\ \beta,\ \gamma\) を使って次のように書ける: \[ \alpha · \overline{OP} + \beta · \overline{OQ} + \gamma · \overline{OR} = 0 \] 加えて逆も成り立つ。 [これは問題 2 の言い換えに過ぎない]
-
\(\overline{AB}\) と \(\overline{AC}\) が同一直線上にない二つの変位で \[ \alpha · \overline{AB} + \beta · \overline{AC} = \gamma · \overline{AB} + \delta · \overline{AC} \] が成り立つなら、\(\alpha = \gamma\) かつ \(\beta = \delta\) である。
[\(AB_{1} = \alpha · AB,\ AC_{1} = \beta · AC\) を取り、平行四辺形 \(AB_{1}P_{1}C_{1}\) を完成させる。すると \(\overline{AP_{1}} = \alpha · \overline{AB} + \beta · \overline{AC}\) が成り立つ。この形を使った \(\overline{AP_{1}}\) の表現方法は一通りしかないことが分かるので、命題が示せる]
-
\(ABCD\) を平行四辺形とする。平行四辺形内部の点 \(Q\) を取り、直線 \(RQS\) と \(TQU\) を辺に平行に取る。\(RU\) と \(TS\) が \(AC\) 上で交わることを示せ。
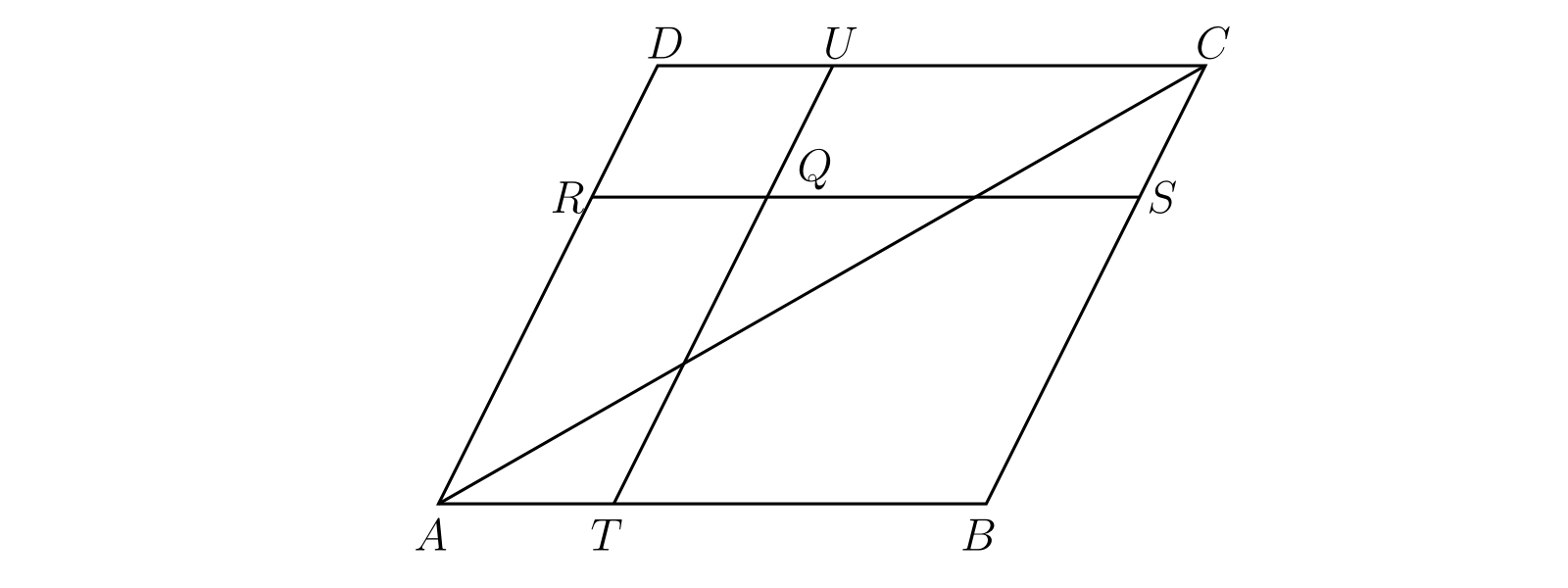 図 21
図 21[比 \(AT:AB\) と \(AR:AD\) を \(\alpha\) と \(\beta\) で表す。このとき次が成り立つ: \[ \begin{gathered} \overline{AT} = \alpha · \overline{AB},\quad \overline{AR} = \beta · \overline{AD}, \\ \overline{AU} = \alpha · \overline{AB} + \overline{AD},\quad \overline{AS} = \overline{AB} + \beta · \overline{AD} \end{gathered} \]
\(RU\) と \(AC\) の交点を \(P\) とすると、三点 \(R,\ U,\ P\) は同一直線上にあるので \[ \overline{AP} = \frac{\lambda}{\lambda + \mu}\, \overline{AR} + \frac{\mu}{\lambda + \mu}\, \overline{AU} \] が成り立つ。ここで \(P\) は \(RU\) を \(\mu : \lambda\) に分割する。ここから次の式が分かる: \[ \overline{AP} = \frac{\alpha\mu}{\lambda + \mu}\, \overline{AB} + \frac{\beta\lambda + \mu}{\lambda + \mu}\, \overline{AD}. \]
一方 \(P\) は \(AC\) 上にあるので、\(\overline{AP}\) は \(\overline{AC}\) の実数倍である。つまり \[ \overline{AP} = k · \overline{AC} = k · \overline{AB} + k · \overline{AD} \] と書ける。よって (問題 5 から) \(\alpha\mu = \beta\lambda + \mu = (\lambda + \mu)k\) が分かり、この式から \[ k = \frac{\alpha\beta}{\alpha + \beta - 1} \] が求まる。この結果の対称性から、\(TS\) と \(AC\) の交点を \(P'\) とすれば同様の議論で \[ \overline{AP'} = \frac{\alpha\beta}{\alpha + \beta - 1}\, \overline{AC} \] が分かる。よって \(P\) と \(P'\) は同一の点を表す]
-
\(ABCD\) を平行四辺形、\(M\) を \(AB\) の中点とする。\(DM\) が \(AC\) を三等分し、\(AC\) が \(DM\) を三等分することを示せ1。
-
最後の二つの例はウィラード・ギブズ著 Vector Analysis から取った。[return]