§45 ド・モアブルの定理

次の命題は加算と乗算の定義から直ちに従う:

1. 二つの複素数の和の実部 (および和の虚部) は二つの実部の和 (および虚部の和) に等しい。
2. 二つの複素数の積の大きさは二つの大きさの積に等しい。
3. 二つの複素数の積の偏角は二つの偏角の和に等しいか、二つの偏角の和から \(2\pi\) 離れた値に等しい。

最後の二つの定理は次の等式として表せる: \[ r(\cos\theta + i\sin\theta) × \rho(\cos\phi + i\sin\phi) = r\rho\{\cos(\theta + \phi) + i\sin(\theta + \phi)\} \] 証明は左辺を計算して \(\cos(\theta + \phi)\) と \(\sin(\theta + \phi)\) に関する三角関数の公式を使えば簡単に行える。さらに一般的に言うと、次が成り立つ: \[ \begin{gathered} r_{1}(\cos\theta_{1} + i\sin\theta_{1}) × r_{2}(\cos\theta_{2} + i\sin\theta_{2}) × \cdots × r_{n}(\cos\theta_{n} + i\sin\theta_{n})\\ = r_{1}r_{2} \cdots r_{n} \{\cos(\theta_{1} + \theta_{2} + \cdots + \theta_{n}) + i \sin(\theta_{1} + \theta_{2} + \cdots + \theta_{n})\} \end{gathered} \]

特に重要なのが \[ r_{1} = r_{2} = \cdots = r_{n} = 1, \quad \theta_{1} = \theta_{2} = \cdots = \theta_{n} = \theta \] とした場合であり、次の式が得られる: \[ (\cos\theta + i\sin\theta)^{n} = \cos n\theta + i\sin n\theta \] ここで \(n\) は正の整数を表す。この結果はド・モアブルの定理 (De Moivre's Theorem) として知られる¹。

また \[ z = r(\cos\theta + i\sin\theta) \] であれば \[ \frac{1}{z} = \frac{1}{r}(\cos\theta - i\sin\theta) \] となる。つまり \(z\) の逆数の大きさは \(z\) の大きさの逆数であり、\(z\) の逆数の偏角は \(z\) の偏角の符号を反転させたものである。ここから (2) と (3) に対応する商に関する定理を導ける:

4. 二つの複素数の商の大きさは二つの大きさの商に等しい。
5. 二つの複素数の商の偏角は二つの偏角の差に等しいか、二つの偏角の差から \(2\pi\) 離れた値に等しい。

また \[ \begin{aligned} (\cos\theta + i\sin\theta)^{-n} & = (\cos\theta - i\sin\theta)^{n}\\ & = \{\cos(-\theta) + i\sin(-\theta)\}^{n}\\ & = \cos(-n\theta) + i\sin(-n\theta) \end{aligned} \] だから、ド・モアブルの定理は正と負の整数 \(\bm{n}\) 全てに対して成立する。

定理 (1)–(5) に次の定理を加える。これも同じく非常に重要である。

6. 任意個の複素数の和の大きさは、大きさの和と等しいかそれより小さい。

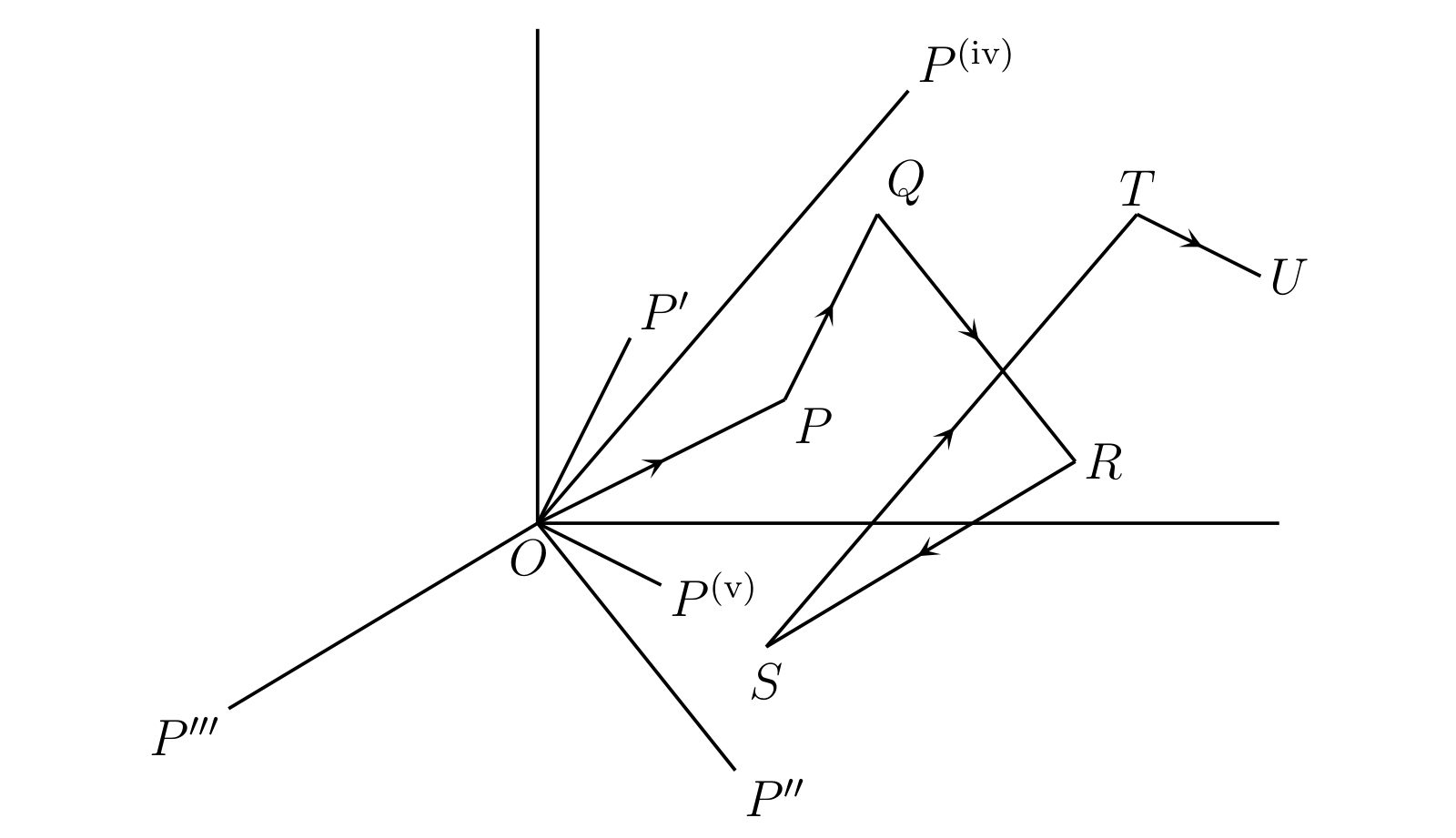
証明は次の通り。\(\overline{OP},\ \overline{OP'},\ \ldots\ \) を複素数に対応する変位とする。\(PQ\) を \(OP'\) と平行で長さが等しいよう取り、\(QR\) を \(OP''\) と平行で長さが等しいように取る。以降も続けて取っていくと、最後の点 \(U\) では次が成り立つ: \[ \overline{OU} = \overline{OP} + \overline{OP'} + \overline{OP''} + \cdots \] \(OU\) の長さは考えている複素数の和の大きさと等しい。一方で複素数の大きさの和は折れ線 \(OPQR \ldots U\) の全長なので、\(OU\) より大きくはならない。

代数だけを使ったこの定理の証明の概略が 例 21.1 にある。

1. \(\cos \theta + i \sin \theta\) を省略して \(\operatorname{Cis} \theta\) と表記すると便利なことがある。ハークネスとモーレイによって導入されたこの表記を使うと、ド・モアブルの定理は \((\operatorname{Cis}\theta)^{n} = \operatorname{Cis}n\theta\) と表せる。^[return]