第四章 正整数関数の極値

§50 正整数関数

第二章では実変数 \(x\) の関数という概念についてたくさんの例を使って議論したが、説明に使った関数の間で大きく異なる重要な特徴が一つあった: 全ての \(x\) に対して定義される関数もあれば、有理数に対してだけ定義される関数もあり、さらに整数に対してだけ定義される関数もあった。

(vii) のように正の整数 \(x\) に対してだけ定義される関数を考える。この関数は二つの少しだけ異なる視点から捉えられる。まずこれまでと同様に、実数変数 \(x\) の関数が \(x\) の一部の値 (つまり正の整数) に対してだけ定義されたものであり、他の \(x\) の値については定義されないとみなす考え方がある。そしてもう一つ、正の整数でない \(x\) の値を全く考慮せずに、関数を正整数変数 \(\bm{n}\) の関数とみなす考え方がある。後者の場合 \(n\) は \[ 1,\ 2,\ 3,\ 4,\ \ldots. \] という値を取る。そして関数を \[ y = \phi(n) \] と表記し、\(y\) を全ての \(n\) に対して定義された \(n\) の関数とみなす。

全ての \(x\) に対して定義された任意の関数から全ての \(n\) に対して定義された関数が作れるのは明らかである。例えば \(y = x^{2}\) から \(y = n^{2}\) を作るには、正の整数でない \(x\) とそれに対応する \(y\) を無視すればよい。一方で全ての \(n\) で定義された関数からは、正の整数でない \(x\) に対応する \(y\) に好きな値を割り当てることで、\(x\) の関数を無数に作れる。

§51 補間

\(n\) の関数が与えられたときに、\(x\) が正の整数のときその関数と同じ値を取る \(x\) の関数を求める問題は、高等数学において非常に重要である。これは関数補間問題 (problem of functional interpolation) と呼ばれる。

しかしこれは、この条件を満たす \(x\) の関数を適当に一つ見つける問題ではない: 上述の通り定義されてない部分には好きな値を割り当てられるので、この問題はあまりにも簡単すぎる。例えば \(n\) の関数の値が \(x\) の関数の値の全てだとみなして他の値では値を持たないとできるが、これは明らかに私たちが望むものではない。必要なのは、\(x\) の(できる限り単純な) 式であって \(x = 1,\ 2,\ \ldots\) で与えられた関数と同じ値を持つものである。

\(n\) が最初から式で定義される場合など、補間問題に明らかな解が存在することもある。例えば \(y = \phi(n)\) で \(\phi(n)\) が \(n^{2}\) や \(\cos \pi\) といった関数なら、こういった関数は \(n\) が正の整数でなくても意味を持つので、\(x\) の関数 \(y = \phi(x)\) を自然に考えられる。ただこの非常に単純な場合でさえ、同程度に明らかな別の解が簡単に見つかる。例えば \(\sin n\pi = 0\) なので \[ y = \phi(x) + \sin x\pi \] は \(x = n\) に \(\phi(n)\) という値を割り当てる。

\(\phi(n)\) が式として定義されていても、その式が一部の \(x\) で値を持たないというケースもある。例えば \((-1)^{n}\) がそうである (\(x\) が無理数、または \(x\) が有理数で分母が偶数のとき値を持たない)。ただし全ての \(x\) で定義されるよう式を変形できる可能性もある。\((-1)^{n}\) の例であれば \[ (-1)^{n} = \cos n\pi \] が整数 \(n\) に対して成り立つので、関数 \(\cos x\pi\) はこの補間問題の解となる。

\(\phi(x)\) が正の整数以外の実数に対して定義されていても、全てに対して定義されるわけではないという場合もある。例えば \(y = n^{n}\) からは \(y = x^{x}\) という式が導かれるが、この式が意味を持つのは残りの \(x\) の一部だけである。正の \(x\) だけを考えるとすれば、(初等代数の有理指数の定義を使うとして) \(x^{x}\) は \(x\) が有理数のときに意味を持つものの、\(x\) が無理数のときは (少なくとも現在の私たちには) 意味をなさない。よってこの補間問題は、\(x^{x}\) を \(x\) が無理数の場合でも意味を持つよう定義を拡張する問題となる。この拡張方法は後述する。

続いて \[ y = 1 · 2 \cdots n = n! \] を考える。\(x\) が正の整数以外の値のとき \(x!\) は意味を持たないので、\(x = n\) で \(n!\) となる簡単な \(x\) の式は存在しない。実はこれは補間問題を解決するための試みが数学における重要な進歩に結び付いたケースであり、補間としての条件を満たすだけではなく他にも興味深い重要な性質をいくつも兼ね備えた関数 (ガンマ関数, Gamma-function) の発見に数学者は成功している。

§52 有限クラスと無限クラス

先に進む前に、純粋数学において頻出する抽象的で論理的なこの概念について少し説明する必要がある。

まず、読者はクラス (a class) という概念を理解しているだろうと思う。「クラス」を論理的に細かく議論する必要はない: クラスとはとある性質を持つ物や対象を集めたり揃えたりしたものだと大雑把に捉えれば十分であり、そのとき性質は単純なものでも複雑なものでも構わない。例えば英国臣民のクラス・代議士のクラス・正の整数のクラス・実数のクラスなどが考えられる。

さらに読者は、有限クラスおよび無限クラスという言葉の意味も理解していると思う。例えば英国臣民のクラスは有限クラスである: 過去・現在・未来の英国臣民を全てを集めれば、その集まりは有限の大きさ \(n\) を持つ。もちろん \(n\) の正確な値は分からない。ただ現在の英国臣民のクラスなら、理論上は \(n\) の値を実際に数えて確認できる。国勢調査が正確であればの話ではあるが。

これに対して、正の整数のクラスは有限ではなく無限である。より正確に表現すれば「\(n\) として任意の正の整数、例えば \(1000\) や \(1,000,000\) あるいは考え得る好きな数を取ると、正の整数の個数は \(n\) より大きい」が成り立つ。 例えば考えた数が \(1,000,000\) だとすれば、明らかに正の整数は \(1,000,001\) 個以上ある。同様に有理数のクラスや実数のクラスも無限と分かる。この事実を「正の整数は無限個ある」と表現すると分かりやすい。ただしこう言ったときに意味するのが、クラスの要素数が \(1000\) とか \(1,000,000\) といった有限の数でないことだけであると必ず意識しておかなければならない。

§53 \(n\) が大きいときの \(n\) の関数の性質 (その 1)

§50–§51 で考えた「\(n\) の関数」に戻る。\(n\) の関数は第二章で考えた \(x\) の関数と様々な点で異なるが、共通する基礎的な性質が一つある: 関数の値が定義される変数の値を集めると無限クラスになる。これからの議論の基礎となるのがこの事実であり、次章で見るようにこの議論は \(x\) の関数に対しても適用できる。

\(\phi(n)\) を任意の \(n\) の関数、\(P\) を \(\phi(n)\) に関する任意の性質 (例えば「正の整数である」や「\(1\) より大きい」など) とする。\(n = 1,\ 2,\ 3,\ \ldots\) のそれぞれについて \(\phi(n)\) が性質 \(P\) を持つかどうかを考えると、次の三つの可能性がある:

1. 全ての \(n\) または有限個の例外を除いた全ての \(n\) で \(\phi(n)\) が性質 \(P\) を持つ。
2. 全ての \(n\) または有限個の例外を除いた全ての \(n\) で \(\phi(n)\) が性質 \(P\) を持たない。
3. (a) でも (b) でもない。

(b) が成り立つなら \(\phi(n)\) が成り立つ \(n\) の値は有限クラスを構成し、(a) が成り立つなら \(\phi(n)\) が成り立たない \(n\) の値は有限クラスを構成する。三番目の場合にはどちらも無限クラスになる。具体的な例を考えよう。

1. \(\phi(n) = n\) で \(P\) が「正の整数である」なら、全ての \(n\) について \(\phi(n)\) は性質 \(P\) を持つ。 これに対して \(P\) を「\(1000\) 以上の正の整数である」とすれば、\(\phi(n)\) は有限個の例外を除いた全ての \(n\) で成り立つ。例外は \(1,\ 2,\ 3,\ \ldots,\ 999\) である。いずれの場合でも (a) が成り立つ。
2. \(\phi(n) = n\) で \(P\) が「\(1000\) より小さい」なら、(b) が成り立つ。
3. \(\phi(n) = n\) で \(P\) が「奇数である」なら、(c) が成り立つ。\(n\) が奇数なら \(\phi(n)\) は奇数、\(n\) が偶数なら \(\phi(n)\) は偶数であり、偶数の \(n\) と奇数の \(n\) はどちらも無限クラスを構成するためである。

§54 \(n\) が大きいときの \(n\) の関数の性質 (その 2)

\(\phi(n)\) と \(P\) が前節の命題 (a) を満たす、つまり有限個の例外を除いた全ての \(n\) で \(\phi(n)\) が成り立つとする。例外の数を \(N\) として、全ての例外を \[ n_{1},\ n_{2},\ \ldots,\ n_{N} \] と表記する。当然これら \(N\) 個の値が最初の \(N\) 個の値 \(1,\ 2,\ \ldots,\ N\) である必要はない。実際に考える関数ではたいてい例外が \(1,\ 2,\ \ldots,\ N\) になるが、そうでなくとも \(n \gt n_{N}\) なら \(\phi(n)\) が性質 \(P\) を持つと言えればよい。例えば \(n\) 番目の素数は奇数となるのは \(n \gt 2\) のときであり、\(n = 2\) が唯一の例外となる。あるいは \(1/n \lt .001\) となるのは \(n \gt 1000\) のときで、最初から \(1000\) 個の \(n\) の値が例外となる。あるいは \[ \frac{1000\{1 + (-1)^{n}\}}{n} \lt 1 \] となるのは \(n \gt 2000\) のときで、例外は \(2,\ 4,\ 6,\ \ldots,\ 2000\) となる。つまり、こういった場合には最初の有限個より後ろの全ての \(\bm{n}\) が考えている性質を持つ。

これからこの事実を、\(\phi(n)\) が「大きい \(n\) で成り立つ」「非常に大きい \(n\) で成り立つ」「十分に大きい全ての \(n\) で成り立つ」などと表現する。そしてこのとき「\(\bm{\phi(n)}\) は大きな \(\bm{n}\) に対して性質 \(\bm{P}\) を持つ」と言う (性質 \(P\) は不等式で表されることが多い)。これはとある有限の値 \(n_{0}\) があって「\(n_{0}\) 以上の全ての \(n\) で \(\phi(n)\)」が成り立つことを意味する。例えば上記の例では、\(n_{0}\) として \(n_{N}\) (最大の例外) より大きい任意の数を取れる: \(n_{N} + 1\) とするのが自然だろう。

よって「大きい素数は全て奇数である」あるいは「大きい \(n\) に対して \(1/n\) は \(.001\) より小さい」といった命題の意味が定まる。読者はこういった命題における「大きい」という言葉の使い方をよく納得しておかなければならない。実のところ数学における大きいという言葉には決まった基準が存在せず、その意味では日常生活で使う「大きい」と大差ない。日常生活において、あるときには大きい数字も別のときには小さくなる例は当たり前のようにある: サッカーで \(6\) ゴールは大きな得点だが、クリケットで \(6\) ランは大きいとは言えない。クリケットの \(400\) ランは大きいが、£ \(400\) の収入はそうでもない。そして数学でも、一般的に言って大きい (large) は十分に大きい (large enough) を意味する。あるとき十分大きい数字も、別のときには十分大きくない可能性がある。

「大きい \(n\) に対して \(\phi(n)\) は性質 \(P\) を持つ」という主張が何を意味するのか理解できたと思う。この章ではこういった命題について考えていく。

§55 「\(n\) が無限大に向かうとき」について

これまで考えたことを少し異なる視点から観察する自然な方法がある。\(n\) が順に \(1,\ 2,\ 3,\ \ldots\) という値を取ると考える。「順に」という言い回しは時間の経過を暗に示しているが、例えば \(n\) が決まった時間 (例えば一秒) ごとに進むと考えればよい。\(n\) は時間の経過と共に大きくなり、その大きさは限りがない。私たちがどんなに大きな数 (例えば \(2147483647\)) を想像したとしても、\(n\) がその数よりも大きくなる瞬間がある。

この際限ない \(n\) の増加を表す簡便な表現として「\(\bm{n}\) が無限大に向かうとき (\(n\) tends to infinity)」あるいは「\(n \to \infty\)」をこれから使うことにする。ここで最後の記号 \(\infty\) は無限大を表す。「向かう」からは「順に」と同様に時間の経過が示唆されるので、上述のように \(n\) が時間と共に変化すると考える。ただしこれは考える上でそうすると分かりやすいだけに過ぎない。変数 \(n\) は論理的な対象であって、それ自体は時間と何の関係もない。

\(n\) が「\(\infty\) に向かう」と言ったとき、それは考えている \(n\) の値が大きくなり続ける終わらない列をなすことを意味する。読者はこの事実を強く心に刻んでおかなければならない。特に「無限大」という数は存在しない: 例えば \[ n = \infty \] と書いたところで、この式は全く意味を持たない。\(n\) が \(\infty\) と等しくなることは原理的にあり得ない。「\(\infty\) と等しい」が意味を持たないからである。さらに言えば、現在の私たちに対して \(\infty\) が意味を持つのは上に示した意味で「\(\infty\) に向かう」と言ったときだけであり、それ以外のときには意味を持たない。以降では \(\infty\) という記号に関連した他の言い回しに意味を与えていくが、そのときには次のことを常に意識する必要がある:

1. \(\bm{\infty}\) 自体には意味がない。ただし \(\bm{\infty}\) を含んだ言い回しは意味を持つ場合がある。
2. 記号 \(\infty\) を含んだ言い回しが意味を持つ全ての場合において、その言い回しが意味を持つ理由は、以前に特別な定義を通してその言い回しに意味を与えたからである。

この定義から次の事実がすぐに分かる: 大きな \(n\) に対して \(\phi(n)\) が性質 \(P\) を持ち、\(n\) が今説明した意味で「\(\infty\) に向かう」なら、いずれ考える \(n\) は十分大きくなり、\(\phi(n)\) が性質 \(P\) を持つ。さらに「\(n\) が十分大きいときに \(\phi(n)\) が持つ性質は何か？」という問題を言い換えると「\(n\) が \(\infty\) に向かうとき、\(\phi(n)\) はどのように振る舞うか？」となることも分かる。

§56 \(n\) が無限大に向かうときの \(n\) の関数の挙動 (その 1)

続いてこれまでの内容を使って、高等数学に絶え間なく登場するあの種の命題が持つ意味の議論に進む。例として (a)「\(n\) が大きいとき \(1/n\) は小さい」と (b)「\(n\) が大きいとき \(1 - (1/n)\) は \(1\) にほぼ等しい」という二つの命題を考える。一見すると自明に思えるこれらの命題にも、注意を必要とする点がたくさんある。まずは少し単純な (a) から見ていく。

以前に「\(n\) が大きいとき \(1/n\) は \(.01\) より小さい」という命題を考えた。これは \(n\) がとある値 (具体的には \(100\)) より大きいときに \(1/n \lt .01\) が成り立つことを意味する。同様に「\(n\) が大きいとき \(1/n\) は \(.0001\) より小さい」も成り立つ: \(n \gt 10000\) なら \(1/n \lt .0001\) となる。この命題は \(.01\) や \(.0001\) を \(.000001\) あるいは \(.00000001\) としても、あるいは好きな正の値としてもなお成り立つ。

「\(n\) が大きいとき \(1/n\) は \(.001\) より小さい」という形をした全ての命題、つまり \(.001\) の部分を \(.0001\) や \(.000001\) をはじめとしたもっと小さな任意の数と取り換えた全ての命題が成り立つことを表す表現があった方が望ましい。これを表すのが「\(\varepsilon\) がどれだけ小さかろうと、\(n\) が十分大きければ \(1/n \lt \varepsilon\) が成り立つ」という言い回しである。そしてこの命題は明らかに正しい。\(n \gt 1/\varepsilon\) なら \(1/n \lt \varepsilon\) なので、"十分に大きい" \(n\) の値とは \(1/\varepsilon\) より大きい全ての値である。この表現は実際には込み入った事実を意味しており、\(\varepsilon\) に \(.01\) といった具体的な値を与えて得られる全ての文の集まりを意味している。もちろん \(\varepsilon\) が小さければそれだけ \(1/\varepsilon\) も大きくなり、"十分に大きい" \(n\) の最小値も大きくなる: \(\varepsilon\) がある値のときに十分に大きい \(n\) も、\(\varepsilon\) がそれより小さくなればそうでなくなる。

前段落の二つ目の鍵括弧にある命題こそが (a) 「\(n\) が大きいとき \(1/n\) は小さい」の本当の意味である。同様に (b) が実際に意味するのは「\(\phi(n) = 1 - (1/n)\) なら、"十分大きい \(n\) に対して \(1 - \phi(n) \lt \varepsilon\)" という命題が \(\varepsilon\) にどんな値 (例えば \(.01\) や \(.0001\)) を与えたとしても成り立つ」である。命題 (b) が成り立つのは \(1 - \phi(n) = 1/n\) から分かる。

(a) と (b) が表す事実を表現するのに使われる方法がもう一つあり、これは §55 の考え方を使っている。具体的には「\(n\) が大きいとき \(1/n\) は小さい」と言う代わりに「\(n\) が \(\infty\) に向かうとき \(1/n\) は \(0\) に向かう」と表現する。同様に「\(n\) が \(\infty\) に向かうとき \(1 - (1/n)\) は \(1\) に向かう」と言う。この二つの命題はそれぞれ (a) および (b) と正確に同値である。つまり

• \(n\) が大きいとき \(1/n\) は小さい
• \(n\) が \(\infty\) に向かうとき \(1/n\) は \(0\) に向かう

はどちらも同じことを表しており、次の正確な表現と同値である:

• \(\varepsilon\) が正の実数なら、\(\varepsilon\) がどれだけ小さくとも、十分大きい \(n\) に対して \(1/n \lt \varepsilon\) が成り立つ

これをさらに正確に言えば次のようになる:

• \(\varepsilon\) が正の整数なら、\(\varepsilon\) がどれだけ小さくとも、\(n_{0}\) より大きい全ての \(n\) で \(1/n \lt \varepsilon\) が成り立つように \(n_{0}\) を選べる

最後の命題における \(n_{0}\) は当然 \(\varepsilon\) の関数である。この事実を強調するために \(n_{0}\) ではなく \(n_{0}(\varepsilon)\) と書く場合もある。

関数 \(1/n\) が持つこの性質を表現する方法をさらにもう一つ導入する。「\(n\) が \(\infty\) に向かうときの \(1/n\) の極限 (limit) は \(0\) である」と言うことにする。そしてこれを \[ \lim_{n\to\infty} \frac{1}{n} = 0 \] あるいは単に \(\lim(1/n) = 0\) と表記する。「\(n \to \infty\) のとき \(1/n \to 0\)」と書くこともある。これは「\(n\) が \(\infty\) に向かうとき \(1/n\) は \(0\) に向かう (\(1/n \to 0\) である)」を意味する。同様に \[ \lim_{n\to\infty} \left(1 - \frac{1}{n}\right) = 1,\quad \lim \left(1 - \frac{1}{n}\right) = 1 \] あるいは \(1 - (1/n) \to 1\) と表記する。

§57 \(n\) が無限大に向かうときの \(n\) の関数の挙動 (その 2)

続いて別の例を考える: \(\phi(n) = n^{2}\) とする。このとき「\(n\) が大きいとき \(n^{2}\) は大きい」が成り立つ。この命題を正確に表現すると次のようになる:

• \(\Delta\) を任意の正の整数とすると、\(\Delta\) がどれだけ大きくとも、十分大きい \(n\) で \(n^{2} \gt \Delta\) となる。
• \(n_{0}(\Delta)\) 以上の全ての \(n\) で \(n^{2} \gt \Delta\) となる \(n_{0}(\Delta)\) を見つけられる。

当然これを「\(n\) が \(\infty\) に向かうとき \(n^{2}\) は \(\infty\) に向かう」あるいは「\(n^{2}\) は \(n\) と共に \(\infty\) へ向かう」と表現し、 \[ n^2 \to \infty \] と書く。

最後に関数 \(\phi(n) = -n^{2}\) を考える。この場合 \(n\) が大きいとき \(\phi(n)\) は大きくなるが、負方向に大きくなる。このとき「\(n\) が \(\infty\) に向かうとき \(-n^{2}\) は \(-\infty\) に向かう」と言い表し、 \[ -n^{2} \to -\infty \] と書く。ここで \(-\infty\) という記号が使われるので、\(n^{2} \to \infty\) を \(n^{2} \to + \infty\) として、一般的には \(\infty\) の代わりに \(+\infty\) と書いて記号が統一させた方が分かりやすい場合もある。

ここで繰り返しになるが、上述の文において \(\infty,\ +\infty,\ -\infty\) と言った記号がそれ自体では意味を持たないことを強調しておく。これまでに説明してきた特別な使われ方をしたときに初めて意味が付与される。

§58 極限の定義 (その 1)

以上の議論を終えれば、極限 (limit) の一般的な概念を説明する準備が整う。大雑把に言って「\(n\) が大きいときに \(\phi(n)\) が \(l\) にほぼ等しい」なら「\(n\) が \(\infty\) に向かうときに \(\phi(n)\) が極限 \(l\) に向かう」と言う。これまでの説明が分かっていればこの文の意味は明確だと思うが、厳密な数学的定義とするにはこれだけでは正確さが十分でない。正確には「十分大きな \(n\) について、\(\phi(n)\) と \(l\) の差が \(\varepsilon\) より小さい」と表現しなければならない。この命題は \(\varepsilon = .01\) でも \(\varepsilon = .0001\) でも正しく、さらに全ての正の実数 \(\varepsilon\) に対して正しい。\(\varepsilon\) がどんな値だったとしても、とある有限の \(n_{0}(\varepsilon)\) より後の全ての \(n\) について \(\phi(n)\) と \(l\) の間が \(\varepsilon\) より小さくなる。もちろん一般的に言って \(\varepsilon\) が小さいほど \(n_{0}\) は大きくなる。

こうして正式な定義が導かれる:

\(\phi(n)\) と \(l\) の差は正の実数 \(|\phi(n) - l|\) で表すことが多い。これは \(\phi(n) - l\) と \(l - \phi(n)\) の正の方と等しく、§44 で定義した \(\phi(n) - l\) の大きさの定義と合致する。ただし今の段階では正と負の実数だけを考えている。

この記法を使えば、定義を次のように短く表現できる: 任意の正の実数 \(\varepsilon\) が与えられたとき、\(\varepsilon\) がどれだけ小さくとも、\(n \geq n_{0}(\varepsilon)\) なら \(|\phi(n) - l| \lt \varepsilon\) となる \(n_{0}(\varepsilon)\) を見つけられるとする。このとき「\(n\) が \(\infty\) に向かうとき \(\phi\) は極限 \(l\) 向かう」と言い、次のように書く: \[ \lim_{n \to \infty} \phi(n) = l \]

§59 極限の定義 (その 2)

極限の定義は次のように図示できる。\(\phi(n)\) のグラフは \(n = 1,\ 2,\ 3,\ \ldots\) に対応する無数の点からなる。

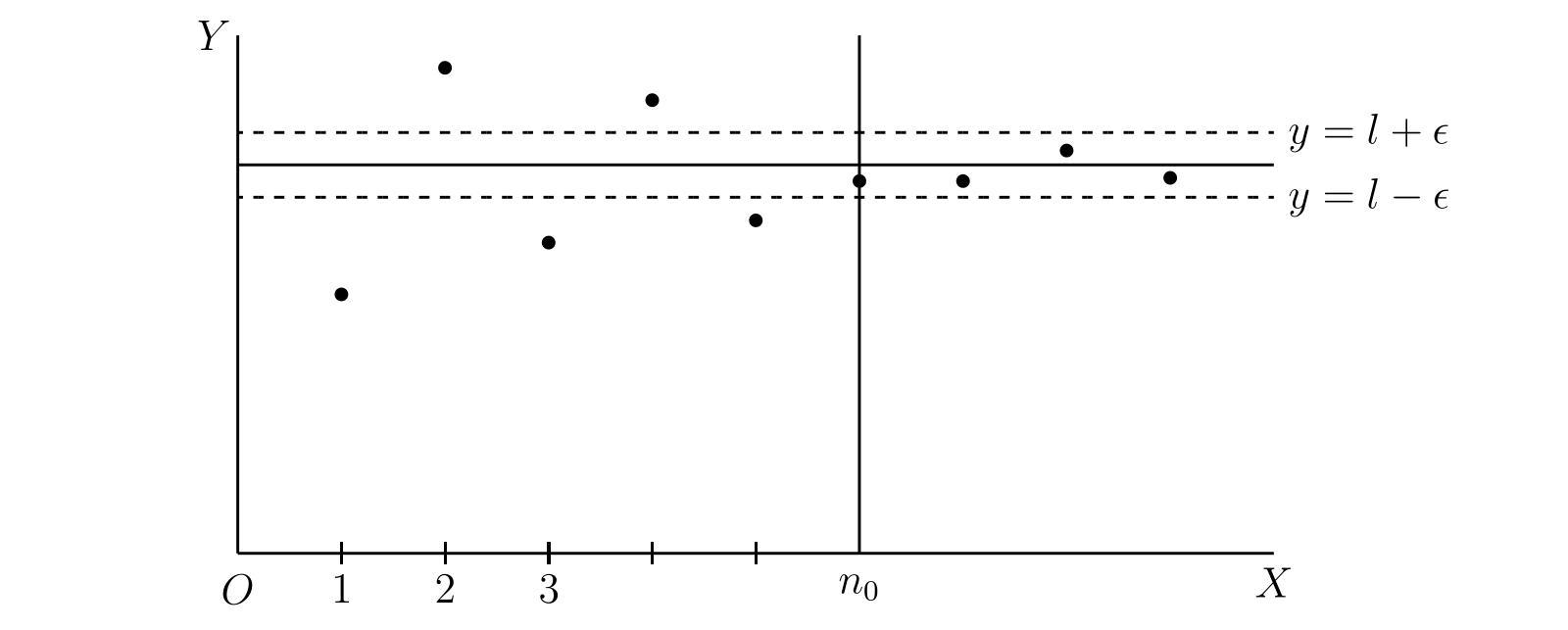
直線 \(y = l\) を描き、そこから \(\varepsilon\) だけ離れた平行な二直線 \(y = l - \varepsilon,\ y = l + \varepsilon\) を描く。すると \[ \lim_{n \to \infty} \phi(n) = l \] となるのは、二つの直線の隙間がどれだけ小さくとも、直線 \(x = n_{0}\) を引いてこの直線よりも右にある全ての点が二つの直線の間にあるようにできるときとなる。この幾何学的な定義の捉え方は、正の整数ではなく全ての実数に対して定義される関数を考えるときに特に重要となる。

§60 極限の定義 (その 3)

\(n\) が \(\infty\) に向かうときに極限を持つ \(n\) の関数については以上となる。次は \(n^{2}\) や \(-n^{2}\) のように、正および負の無限大に向かう関数について同様の定義を考える。ここまでを理解した読者であれば次の定義を簡単に理解できるだろう:

正確さを犠牲にした表現を使えば「十分大きい \(n\) を考えれば \(\phi(n)\) を好きなだけ大きくできる」となる。この表現では定義の重要な点、つまり \(\phi(n)\) が \(n \geq n_{0}(\Delta)\) を満たす全ての \(n\) で \(\Delta\) より大きくならなければならず、一部が大きくなるだけでは不十分である点が曖昧になってしまうが、意味が分かっているならこう書いても問題はない。

\(\phi(n)\) が \(+\infty\) に向かうとき \[ \phi(n) \to +\infty \] と書く。負の無限大に向かう関数の定義は読者に任せる。

§61 極限の定義に関して

読者は次の点に注意すべきである。

1. 明らかに、\(\phi(n)\) の値を有限個の \(n\) で変化させても \(n\) が無限大に向かうときの \(\phi(n)\) の挙動は変化しない。例えば \(1/n\) は \(n\) が \(\infty\) に向かうとき \(0\) に向かうが、\(1/n\) の値を有限個だけ適当に変化させれば新しい関数を無数に作れる。例として \(n = 1,\ 2,\ 7,\ 11,\ 101,\ 107,\ 109,\ 237\) で \(3\) となり、他の \(n\) では \(1/n\) となる関数 \(\phi(n)\) を考えると、この関数は最初の \(1/n\) と同様 \(\lim\phi(n) = 0\) を満たす。あるいは \(n = 1,\ 2,\ 7,\ 11,\ 101,\ 107,\ 109,\ 237\) で \(3\) となり、それ以外の \(n\) で \(n^{2}\) となる関数を \(\phi(n)\) とすれば、\(\phi(n) \to +\infty\) が成り立つ。

2. 一方で無限個の \(\phi(n)\) の値を変化させると、一般には \(n\) が \(\infty\) に向かうときの挙動が変化する。例えば関数 \(1/n\) について、\(n\) が \(100\) の倍数のときの値を全て \(1\) に変更すると \(\lim\phi(n) = 0\) は成り立たなくなる。値が変わるのが有限個である限り、\(\phi(n)\) が変更された全ての \(n\) に対応する \(n_{0}\) より大きい \(n_{0}\) を必ず選べる。例えば上述の例では常に \(n_{0} \gt 237\) を取れる。実際には §56 で考えた仮想的な相手が \(3\) より小さな \(\varepsilon\) (前者の例) あるいは \(3\) より大きい \(\Delta\) (後者の例) を示してきた場合にはこの条件が自動的に満たされる。しかし無限個の値を変化させると、\(n_{0}\) としてどれだけ大きな値を取っても、それよりも大きい \(n\) で \(\phi(n)\) が元の関数と異なるものが存在してしまう。

3. 極限の定義において、\(|\phi(n) - l| \lt \varepsilon\) が \(n = n_{0}\) だけではなく \(n \geq n_{0}\) のときも成り立たなければならないという条件はもちろん欠かすことができない。つまり \(n_{0}\) とそれよりも大きい全ての \(n\) で不等式が成り立つ必要がある。例えば最後の例の \(\phi(n)\) では、与えられた \(\varepsilon\) に対して \(n = n_{0}\) のとき \(|\phi(n)| \lt \varepsilon\) となるよう \(n_{0}\) を選ぶことはできる: 十分に大きくて \(100\) の倍数でない \(n\) を選べばよい。しかしそう選んだ \(n_{0}\) も、全ての \(n \geq n_{0}\) で \(|\phi(n)| \lt \varepsilon\) とはならない: \(n_{0}\) より大きい任意の \(100\) の倍数はこの不等式を満たさない。

4. \(\phi(n)\) が常に \(l\) より大きいなら、\(|\phi(n) - l|\) を \(\phi(n) - l\) とできる。例えば \(n\) が無限大に向かうときに \(1/n\) が \(0\) に向かうことを示すには、\(n \geq n_{0}\) のとき \(1/n \lt \varepsilon\) が示せればよい。一方で \(\phi(n) = (-1)^{n}/n\) の場合には、\(l\) は \(0\) で変わらないものの、\(\phi(n) - l\) が正にも負にもなる。このような場合には条件を \(|\phi(n) - l| \lt \varepsilon\) としなければならない。今の例では \(|\phi(n)| \lt \varepsilon\) とする。

5. 極限 \(l\) が \(\phi(n)\) が取る値と同じになることもある。例えば全ての \(n\) に対して \(\phi(n) = 0\) なら、明らかに \(\lim\phi(n) = 0\) となる。あるいは上の (2) と (3) のように関数 \(1/n\) の値を置き換え、そのとき \(n\) が \(100\) の倍数のとき (\(1\) ではなく) \(0\) とする。そうすると \(\phi(n)\) は \(n\) が \(100\) の倍数のとき \(0\) でそれ以外のとき \(1/n\) となる。こうしたとしても \(n\) が無限大に向かうときの \(\phi(n)\) の極限は \(0\) で変わらず、この関数は極限と同じ値を無限個の \(n\) で取る: 具体的には \(100\) の倍数で \(\phi(n) = 0\) となる。

   一方で一般には \(\bm{n}\) の関数がある \(\bm{n}\) で極限と同じ値を取るとは限らない。これは \(\phi(n) = 1/n\) の場合を考えれば十分である。極限は \(0\) だが、どんな \(n\) を与えてもこの関数が \(0\) になることはない。

   次の事実はどれだけ強く意識しても意識しすぎることはない: 極限は関数の値ではない。極限は関数の値とは全く異なる値であり、その定義に関数の値が使われていて、関数の値と等しくなることもあるというだけに過ぎない。例えば \[ \phi(n) = 0,\ 1 \] という関数では、全ての \(\phi(n)\) が極限と等しい。また \[ \phi(n) = \frac{1}{n},\quad \frac{(-1)^{n}}{n},\quad 1 + \frac{1}{n},\quad 1 + \frac{(-1)^{n}}{n} \] では、極限は \(\phi(n)\) のどれとも等しくない。さらに \[ \phi(n) = (\sin\tfrac{1}{2}n\pi)/n,\quad 1 + \{(\sin\tfrac{1}{2}n\pi)/n\} \] (\(\sin\frac{1}{2}n\pi\) が常に \(1\) 以下なので、\(n\) が \(\infty\) に向かうときのこの関数の極限は \(0\) および \(1\) だと分かる) では、極限は偶数の \(n\) に対応する値と等しいものの、奇数の \(n\) に対応する値とは等しくない。

6. 関数の値の絶対値が \(n\) が大きいときに常にとても大きいにもかかわらず、それが \(+ \infty\) や \(-\infty\) に向かわないことがあり得る。例としては \(\phi(n) = (-1)^{n} n\) がある。関数が \(+\infty\) や \(-\infty\) に向かうのは、ある \(n\) より後ろで符号が一定であるときに限られる。

§62 振動関数

例えば前節の最後の例のように関数の取る値が周期的な列をなす場合、その関数は振動する。ただしこのような特殊な挙動をせずに振動する場合もある。関数が振動するのは他に特別なことをしないときであり、関数の振動は純粋に否定的に定義される。

もっとも単純な振動関数の例を次に示す: \[ \phi(n) = (-1)^{n} \] \(\phi(n)\) は \(n\) が偶数なら \(+1\) で \(n\) が奇数なら \(-1\) であり、二つの値を交互に取る。次に \[ \phi(n) = (-1)^{n} + \frac{1}{n} \] を考える。この関数の取る値は \[ -1 + 1,\quad 1 + \frac{1}{2},\quad -1 + \frac{1}{3},\quad 1 + \frac{1}{4},\quad -1 + \frac{1}{5},\ \ldots \] となる。\(n\) が大きいときの関数の値は \(+1\) と \(-1\) にほぼ等しくなる。\(\phi(n)\) が極限あるいは \( \infty\) や \(-\infty\) に向かうことはないので、この関数は振動する: しかし同じ値は繰り返されない。またこの関数の値の大きさが全て \(3/2\) 以下であることも分かる。同様に \[ \phi(n) = (-1)^{n} 100 + \frac{1000}{n} \] も振動する。\(n\) が大きいときの関数の値は \(100\) と \(-100\) にほぼ等しい。この場合の大きさの最大値は \(n = 1\) のときの \(900\) である。次に \(\phi(n) = (-1)^{n}n\) を考えると、関数は \(-1,\ 2,\ -3,\ 4,\ -5,\ \ldots\ \) という値を取る。\(\phi(n)\) は極限にも \(+\infty\) や \(-\infty\) にも向かわないので、この関数は振動する。しかしこの場合には、関数の値の大きさを上から抑える上限が存在しない。この二種類の例から、さらなる定義が必要だと分かる:

§63 振る舞いが分かっている二つの関数の和の振る舞い

これはほとんど明らか⁴である。次のような議論がすぐに頭に浮かぶだろう: 「\(n\) が大きいとき、\(\phi(n)\) はほぼ \(a\) に等しく、\(\psi(n)\) は \(b\) にほぼ等しい。よってその和は \(a + b\) にほぼ等しい」 後はこれを正しく表現すればよい。

\(\varepsilon\) を任意の正の実数 (例えば \(.001,\ .0000001,\ \ldots\)) とする。\(n \geq n_{0}\) で次の条件が成り立つような \(n_{0}\) を見つければよい: \[ |\phi(n) + \psi(n) - a - b| \lt \varepsilon \qquad \text{(1)} \] 第三章で証明したように、二つの数の和の大きさは大きさの和以下なので \[ |\phi(n) + \psi(n) - a - b| \leq |\phi(n) - a| + |\psi(n) - b| \] が成り立つ。よって \(n \geq n_{0}\) で次の条件が満たされるように \(n_{0}\) を選べるなら \(\text{(1)}\) が成り立つと分かる: \[ |\phi(n) - a| + |\psi(n) - b| \lt \varepsilon \qquad \text{(2)} \] そしてこれはもちろん正しい: \(\lim \phi(n) = a\) だから、極限の定義より \(n_{1}\) が存在して \(n \geq n_{1}\) のとき \(|\phi(n) - a| \lt \varepsilon'\) が成り立つ。ここで \(\varepsilon'\) はどれだけ小さくても構わない。よって \(\varepsilon' = \frac{1}{2}\varepsilon\) として \(n \geq n_{1}\) で \(|\phi(n) - a| \lt \frac{1}{2}\varepsilon\) となるようできる。同様に \(n \geq n_{2}\) で \(|\psi(n) - b| \lt \frac{1}{2}\varepsilon\) となる \(n_{2}\) を見つけられる。後は \(\bm{n_{1}}\) と \(\bm{n_{2}}\) の大きい方を \(n_{0}\) として取る。そうすれば \(n \geq n_{0}\) のとき \(|\phi(n) - a| \lt \frac{1}{2}\varepsilon\) かつ \(|\psi(n) - b| \lt \frac{1}{2}\varepsilon\) となって (2) が満たされるので、定理が証明される。

§64 極限に関する諸定理

次の結果は簡単に確認できるだろう:

1. \(\phi(n)\) が極限に向かって \(\psi(n)\) が \(+\infty\) または \(-\infty\) に向かうか無限または有限に振動するなら、\(\phi(n) + \psi(n)\) は \(\psi(n)\) と同じように振る舞う。

2. \(\phi(n) \to +\infty\) で \(\psi(n)\) が \( +\infty\) に向かうか有限に振動するなら、\(\phi(n) + \psi(n) \to +\infty\) が成り立つ。

もちろん二つ目の命題は \(+\infty\) を \(-\infty\) に変えても成り立つ。

3. \(\phi(n) \to + \infty\) かつ \(\psi(n) \to -\infty\) なら、\(\phi(n) + \psi(n)\) は極限に向かう場合もあれば \(+\infty\) または \(-\infty\) に向かう場合もある。あるいは有限または無限に振動する場合もある。

(i) \(\phi(n) = n,\ \psi(n) = -n,\ \) (ii) \(\phi(n) = n^{2},\ \psi(n) = -n,\ \) (iii) \(\phi(n) = n,\ \psi(n) = -n^{2},\ \) (iv) \(\phi(n) = n + (-1)^{n},\ \psi(n) = -n\) (v) \(\phi(n) = n^{2} + (-1)^{n}n,\ \psi(n) = -n^{2}\) がこの五つの可能性を満たす例となる。これ以外の例も作ってみるとよい。

4. \(\phi(n) \to +\infty\) で \(\psi(n)\) が無限に振動するなら、\(\phi(n) + \psi(n)\) は \( +\infty\) に向かう場合もあれば無限に振動する場合もある。ただし極限に向かう、\(-\infty\) に向かう、有限に振動することはない。

\(\psi(n) = \{\phi(n) + \psi(n)\} - \phi(n)\) なので、仮に \(\phi(n) + \psi(n)\) に対して最後の三つのうちどれかが成り立つとすると、これまでの結果から \(\psi(n) \to -\infty\) となって不合理となる。あり得る二つの場合の例としては (i) \(\phi(n) = n^{2},\ \psi(n) = (-1)^{n}n\) と (ii) \(\phi(n) = n,\ \psi(n) = (-1)^{n}n^{2}\) がある。ここでも \(+ \infty\) と \(-\infty\) は交換できる。

5. \(\phi(n)\) と \(\psi(n)\) がどちらも有限に振動するなら、\(\phi(n) + \psi(n)\) は極限に向かうか、有限に振動する。

例えば (i) \(\phi(n) = (-1)^{n},\ \psi(n) = (-1)^{n+1},\ \) (ii) \(\phi(n) = \psi(n) = (-1)^{n}\) とすれば二つの可能性が得られる。

6. \(\phi(n)\) が有限に振動し \(\psi(n)\) が無限に振動するなら、\(\phi(n) + \psi(n)\) は無限に振動する。

仮定から \(\phi(n)\) の絶対値がある値 \(K\) より常に小さいと分かる。\(\psi(n)\) は無限に振動するので、その絶対値は任意の実数 (\(10K,\ 100K,\ \ldots\)) よりも大きくなる。よって \(\phi(n) + \psi(n)\) の絶対値は任意の実数 (\(9K,\ 99K,\ \ldots\)) より大きくなる。よって \(\phi(n) + \psi(n)\) は \(+\infty\) または \(-\infty\) に向かうか、無限に振動する。しかしもし \( +\infty\) に向かうなら \[ \psi(n) = \{\phi(n) + \psi(n)\} - \phi(n) \] も同じく \(+\infty\) に向かうことがこれまでの結果から分かるので、\(\phi(n) + \psi(n)\) は \( +\infty\) に向かわない。同様に \(- \infty\) に向かうこともなく、無限に振動すると分かる。

7. \(\phi(n)\) と \(\psi(n)\) が両方とも無限に振動するなら、\(\phi(n) + \psi(n)\) は極限に向かうか、\(+ \infty\) または \(- \infty\) に向かうか、有限または無限に振動する。

\(\phi(n) = (-1)^{n}n\) で \(\psi(n)\) を \((-1)^{n+1}n,\ \{1 + (-1)^{n+1}\}n,\ -\{1 + (-1)^{n}\}n,\ (-1)^{n+1}(n + 1),\ (-1)^{n}n\) とすれば、五つの可能なケースが全て得られる。

以上の七つの結果は互いに異なる命題を表す。二つの関数の積を考える前に、§63 の定理は \(n \to \infty\) のときの三つ以上の関数の和についても拡張できることを指摘しておく。

§65 振る舞いが分かっている二つの関数の積の振る舞い

二つの関数の積についても同様の定理をそれぞれ示せる。一番重要な定理を次に示す:

\(\phi_{1}(n)\) と \(\psi_{1}(n)\) を \[ \phi(n) = a + \phi_{1}(n), \quad \psi(n) = b + \psi_{1}(n) \] と定義すると、\(\lim\phi_{1}(n) = 0\) と \(\lim\psi_{1}(n) = 0\) が成り立つ。そして \[ \phi(n)\psi(n) = ab + a\psi_{1}(n) + b\phi_{1}(n) + \phi_{1}(n)\psi_{1}(n) \] なので、\(\phi(n)\psi(n) - ab\) の絶対値は \(a\psi_{1}(n),\ b\phi_{1}(n),\ \phi_{1}(n)\psi_{1}(n)\) の絶対値の和以下である。したがって \[ \lim\{\phi(n)\psi(n) - ab\} = 0 \] が分かり、定理が証明される。

言うまでもなく、§63 の定理と同じくこの定理も任意個の関数の積に拡張でき、§64 で和について述べたのと同様の定理は積についても成り立つ。ただし積では、\(n\) が \(\infty\) に向かうときの \(\phi(n)\) の挙動を六種類に場合分けする必要がある。つまり \(\phi(n)\) が (1) \(\bm{0}\) でない極限に向かう、(2) \(0\) に向かう、(3a) \(+\infty\) に向かう、(3b) \(-\infty\) に向かう、(4) 有限に振動する、(5) 無限に振動する、の六つである。ただし一般に (3a) の結果の符号を交換すれば (3b) を得られるので、個別に考える必要はない。

その他の定理を全て長々と考えていては紙面が足りなくなる。例として二つだけをここに示し、他は読者に任せる。残りの定理の定式化はちょうどよい練習問題だろう。

\(\phi(n)\) を \(n\)、\(\psi(n)\) を \(2 + (-1)^{n},\ -2 - (-1)^{n},\ (-1)^{n}\) とすれば三つの可能性が得られる。

例えば (i) \(\phi(n) = \psi(n) = (-1)^{n},\ \) (ii) \(\phi(n) = 1 + (-1)^{n},\ \psi(n) = 1 - (-1)^{n},\ \) (iii) \(\phi(n) = \cos\frac{1}{3}n\pi,\ \psi(n) = \sin\tfrac{1}{3} n\pi\) とする。

この定理は \(\phi(n)\) が定数の場合が特に重要となる。このとき定理は「\(\lim\phi(n) = a\) なら \(\lim k\phi(n) = ka\)」という命題になる。ここから、\(k = 0\) でないなら \(\phi(n) \to +\infty\) のとき \(k\) の符号に応じて \(k\phi(n) \to +\infty\) または \(k\phi(n) \to -\infty\) だと分かる。\(k = 0\) ならもちろん全ての \(n\) に対して \(k\phi(n) = 0\) であり \(\lim k\phi(n) = 0\) となる。また \(\phi(n)\) が有限あるいは無限に振動するなら、\(k = 0\) でない限り \(k \phi(n)\) も同じ振る舞いをする。

§66 振る舞いが分かっている二つの関数の商の振る舞い

もちろん二つの関数の差についても同様の定理が存在し、ここまでの定理の系として簡単に示せる。商 \[ \frac{\phi(n)}{\psi(n)} \] に関する定理を示すには、次の定理をまず証明する。

仮定から \[ \phi(n) = a + \phi_{1}(n) \] と置くと \(\lim\phi_{1}(n) = 0\) であり、そして \[ \left|\frac{1}{\phi(n)} - \frac{1}{a}\right| = \frac{|\phi_{1}(n)|}{|a| |a + \phi_{1}(n)|} \] が成り立つ。\(\lim\phi_{1}(n) = 0\) より、\(n \geq n_{0}\) のときこの値が \(\varepsilon\) 以下になるよう \(n_{0}\) を選べる。

これまでの二つの定理から、商に関する一般的な定理が得られる:

これまでの定理について見た「関連する定理」を、この定理についても定式化・証明・例示してみるとよい。

§67 有理関数の極限

証明は次の通り。\(P\) は定数 \(A\) と正の整数 \(p,\ q,\ \ldots\) を使った次の形の項の和として表せる: \[ A\{\phi(n)\}^{p} \{\psi(n)\}^{q} \cdots \] §65 の定理 (を任意個の関数の積に拡張したもの) から、この項は極限 \(Aa^{p}b^{q}\cdots\) に向かうと分かる。よって §63 の定理の拡張から \(P\) は極限 \(P(a, b, c,\ \ldots)\) に向かう。したがって §66 の定理から示したい式が得られる。

§68 一般的な有理関数の極限

上の一般的な定理は次の非常に重要な問題に適用できる: 「最も一般的な \(n\) の有理関数 \[ S(n) = \frac{a_{0}n^{p} + a_{1}n^{p-1} + \cdots + a_{p}} {b_{0}n^{q} + b_{1}n^{q-1} + \cdots + b_{q}} \] は、\(n\) が \(\infty\) に向かうときどう振る舞うか⁵？」

定理を適用するために、\(S(n)\) を次のように変形する: \[ n^{p-q}\left\{ \biggl(a_{0} + \frac{a_{1}}{n} + \cdots + \frac{a_{p}}{n^{p}}\biggr)\bigg/ \biggl(b_{0} + \frac{b_{1}}{n} + \cdots + \frac{b_{q}}{n^{q}}\biggr) \right\} \] 中括弧の中身は \(R\{\phi(n)\}\) という形をしている。ここで \(\phi(n) = 1/n\) であり、\(n\) が \(\infty\) に向かうとき \(R\) は \(R(0) = a_{0}/b_{0}\) に向かう。そして \(p \lt q\) なら \(n^{p-q} \to 0\)、\(p = q\) なら \(n^{p-q} = 1\) したがって \(n^{p-q} \to 1\)、\(p \gt q\) なら \(n^{p-q} \to +\infty\) となる。よって §65 の定理から \[ \begin{cases} \lim S(n) = 0 & (p \lt q), \\ \lim S(n) = a_{0}/b_{0} & (p = q), \\ S(n) \to +\infty & (p \gt q,\ a_{0}/b_{0} \text{ が正}), \\ S(n) \to -\infty & (p \gt q,\ a_{0}/b_{0} \text{ が負}) \end{cases} \] が分かる。

§69 単調増加関数

\(n\) の関数からなる特殊なクラスで特に重要なのが、\(n\) が \(\infty\) に向かうときの値の変動が常に同じ方向である関数のクラス、つまり常に増加する関数と常に減少する関数からなるクラスである。ただ \(\phi(n)\) が常に増加するなら \(-\phi(n)\) は常に減少するので、二つのケースを別々に考える必要はない。どちらかに対して証明された定理は簡単にもう一方へと拡張できる。

\(\phi(n)\) がいくつかの連続する \(n\) について同じ値を取る場合は除かれていない: 除いたのは減少する場合だけである。例えば \[ \phi(n) = 2n + (-1)^{n} \] は \(n = 0,\ 1,\ 2,\ 3,\ 4,\ \ldots\ \) のときの値が \[ 1,\ 1,\ 5,\ 5,\ 9,\ 9,\ \ldots \] なので、\(n\) に関して単調増加である。さらにこの定義は、ある \(n\) の後が全て定数となる関数も除いていない: 例えば \(\phi(n) = 1\) は単調増加である。ただこういった関数は非常に特殊で \(n\) が \(\infty\) に向かうときの振る舞いも明らかなので、一見不自然に思えるこの定義に大きな問題はない。

このクラスに属する関数についてのきわめて重要な定理がある:

言い換えると、一般的には五つの可能性があった関数の振る舞いが、今考えている特殊な関数については二つしかない。

この定理はデデキントの定理 (§17) の単純な系である。\(\xi\) を任意の実数として、ある \(n\) (およびそれ以降の全ての \(n\)) で \(\phi(n) \geq \xi\) ならクラス \(L\) に、そうでないなら \(R\) に入れることで、実数を二つのクラスに分割する。

このとき \(L\) は確実に存在するが、\(R\) は存在しない場合がある。もし \(R\) が存在しないなら、任意の実数 \(\Delta\) について、十分大きな全ての \(n\) で \(\phi(n) \gt \Delta\) が成り立つ。つまり \[ \phi(n) \to +\infty \] となる。

一方でもし \(R\) が存在するなら、\(L\) と \(R\) は §17 の意味で実数の切断を定義する。この切断に対応する実数を \(a\) とする。\(\varepsilon\) を任意の正の実数とすると全ての \(n\) について \(\phi(n) \lt a + \varepsilon\) であり、\(\varepsilon\) は任意だから \(\phi(n) \leq a\) が分かる。一方で十分大きな \(n\) とそれ以降の全ての \(n\) で \(\phi(n) \gt a - \varepsilon\) なので、 \[ \phi(n)\to a \] が分かる。

後で非常に有用となる系を示す:

極限が \(K\) となる可能性もあることに注意すべきである。例えば \(\phi(n) = 3 - (1/n)\) とすると、全ての \(\phi(n)\) は \(3\) より小さいにもかかわらず極限は \(3\) となる。

\(n\) が大きくなるにつれて \(\phi(n)\) が小さくなる場合に対応する定理や系を自分で書いてみるとよい。

§70 単調増加関数の収束判定

上述の定理がなぜ重要かというと、この定理を使えば \(n\) の関数が \(n \to \infty\) のとき極限に向かうかどうかをあらかじめ極限を予測、推定することなく判定できる場面が非常に多いためである。これは今まで不可能だった。極限の存在とその値が分かっているなら \[ |\phi(n) - l| \lt \varepsilon\quad (n \geq n_{0}) \] という判定法が使える。例えば \(\phi(n) = 1/n\) なら、極限には \(0\) しかあり得ないとすぐに分かる。しかし \[ \phi(n) = \left(1 + \frac{1}{n}\right)^{n} \] が極限に向かうかどうかを判定するときには、極限がそもそも存在するのか、極限が存在したとしてその値は何かが分からない。そのため極限 \(l\) を使う上述の判定法は、\(l\) の存在を判定するのに全く使いものにならない。

§71 ワイエルシュトラスの定理の別証明

§69 の結果を使うと、§19 で示した重要な定理の別証明が可能になる。

\(PQ\) を二つの等しい部分に分ける。二つの部分の少なくとも一方は \(S\) の点を無限に含むので、それを \(P_{1}Q_{1}\) とする (図 28)。両方が無限の点を含むときは左側の部分を選ぶ。

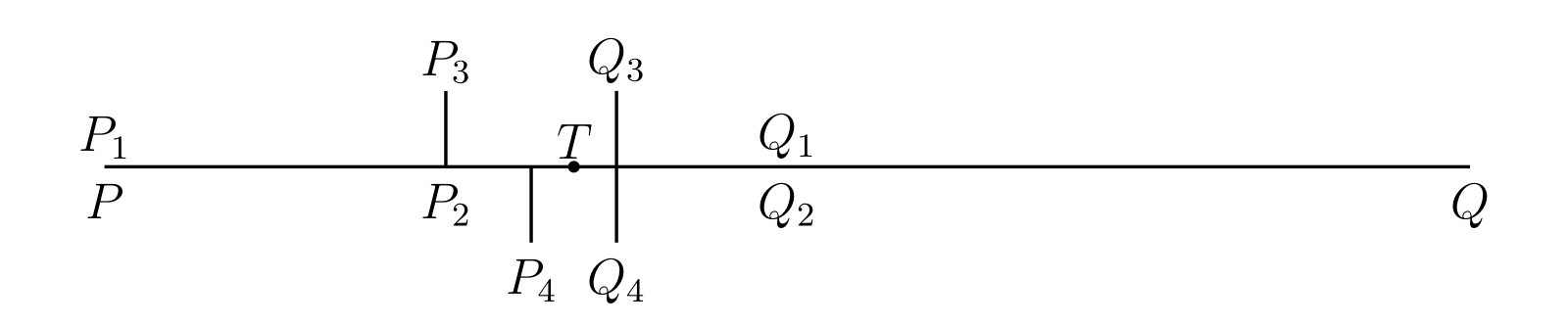
同様に \(P_{1}Q_{1}\) を二つの等しい部分に分ければ、少なくとも一方は \(S\) の点を無限に含む。無限の点を含むのが片方だけならそれを \(P_{2}Q_{2}\) とし、両方が含むときは左側の部分を \(P_{2}Q_{2}\) とする。この操作を繰り返すと区間の無限列 \[ PQ,\quad P_{1}Q_{1},\quad P_{2}Q_{2},\quad P_{3}Q_{3},\quad \ldots, \] を定義できる。各区間は一つ前の区間の半分であり、全ての区間は \(S\) の点を無限に含む。

点 \(P,\ P_{1},\ P_{2},\ \ldots\ \) は左から右へ単調に移動するので、\(P_{n}\) は極限の点 \(T\) に向かう。同様に \(Q_{n}\) も極限の点 \(T'\) に向かう。しかし明らかに、どんな \(n\) に対しても \(TT'\) は \(P_{n}Q_{n}\) よりも小さい。\(P_{n}Q_{n}\) の長さは \(PQ/2^{n}\) であり、\(0\) に向かう。そのため \(T'\) と \(T\) は一致し、\(P_{n}\) と \(Q_{n}\) はどちらも \(T\) に向かう。

このとき \(T\) は \(S\) の集積点となる: \(\xi\) を \(T\) の座標として \(\xi - \varepsilon, \xi + \varepsilon\) という形の区間を考えると、十分大きな \(n\) では \(P_{n}Q_{n}\) がこの区間に完全に含まれる⁶ので、\([\xi - \varepsilon, \xi + \varepsilon]\) は \(S\) の点を無限に含む。

§72 \(x^n\) の極限

§69 の結果を \(\phi(n) = x^{n}\) という特に重要な関数に適用しよう。\(x = 1\) なら \(\phi(n) = 1\) で \(\lim\phi(n) = 1\) となり、\(x = 0\) なら \(\phi(n) = 0\) で \(\lim \phi(n) = 0\) となる。これらの特殊ケースについてこれ以上考える必要はない。

まず \(x\) が正だとする。すると \(\phi(n + 1) = x\phi(n)\) なので、\(x \gt 1\) なら \(\phi(n)\) は \(n\) と共に増加し、\(x \lt 1\) なら \(n\) と共に減少する。

もし \(x \gt 1\) なら、\(x^{n}\) は (明らかに \(1\) より大きい) 極限または \(+\infty\) に向かう。極限 \(l\) に向かうなら 例 25.7 から \(\lim\phi(n + 1) = \lim\phi(n) = l\) であり、ここから \[ \lim\phi(n + 1) = \lim x\phi(n) = x\lim\phi(n) = xl \] となって \(l = xl\) が分かる。しかし \(x\) と \(l\) はどちらも \(1\) より大きいので、これはあり得ない。よって \[ x^{n} \to +\infty\quad (x \gt 1) \] が分かる。

一方で \(x \lt 1\) なら \(x^{n}\) は減少関数であり、極限または \(-\infty\) に向かう。\(x^{n}\) は正だから二番目の選択肢は無視できる。\(\lim x^{n} = l\) とおけば前と同じ理由で \(l = xl\) であり、\(l = 0\) が分かる。つまり \[ \lim x^{n} = 0\quad (0 \lt x \lt 1) \] である。

最後に \(x\) が負の場合を考える。もし \(-1 \lt x \lt 0\) なら、\(x = -y\) とすれば \(0 \lt y \lt 1\) であり \(\lim y^{n} = 0\) が分かる。よって \(\lim x^{n} = 0\) となる。もし \(x = -1\) なら \(x^{n}\) は \(1\) と \(-1\) の間で振動する。最後に \(x \lt -1\) なら、\(x = -y\) とすれば \(y \gt 1\) であり \(y^{n}\) は \(+\infty\) に向かう。よって \(x^{n}\) は正負の符号を交互に取り、その絶対値は任意の数より大きくなる。つまり \(x^{n}\) は無限に振動する。以上の結果を次にまとめる: \[ \begin{alignedat}{2} & \phi(n) = x^{n} \to +\infty & & (x \gt 1),\\ & \lim \phi(n) = 1 & & (x = 1),\\ & \lim \phi(n) = 0 & & (-1 \lt x \lt 1),\\ & \phi(n) \text{ は有限に振動する} & & (x = -1),\\ & \phi(n) \text{ は無限に振動する} \qquad & & (x \lt -1) \end{alignedat} \]

§73 \((1 + \frac{1}{n})^{n}\) の極限

§69 の定理を使うと \(\displaystyle \phi(n) = \left(1 + \frac{1}{n}\right)^{n}\) に関するより難しい問題を解くことができる。

二項定理⁷から次が分かる: \[ \begin{gathered} \begin{aligned} \biggl(1 + \frac{1}{n}\biggr)^{n} & = 1 + n · \frac{1}{n} + \frac{n(n - 1)}{1·2}\, \frac{1}{n^{2}} + \cdots + \frac{n(n - 1)\cdots (n - n + 1)}{1·2\cdots n}\, \frac{1}{n^{n}}\\ & = 1 + 1 + \frac{1}{1·2} \biggl(1 - \frac{1}{n}\biggr) + \frac{1}{1·2·3} \biggl(1 - \frac{1}{n}\biggr) \biggl(1- \frac{2}{n}\biggr) + \cdots\\ \end{aligned} \\ {} + \frac{1}{1·2\cdots n} \biggl(1 - \frac{1}{n}\biggr) \biggl(1 - \frac{2}{n}\biggr)\cdots \biggl(1 - \frac{n - 1}{n}\biggr) \end{gathered} \]

この式の第 \(p + 1\) 項 \[ \frac{1}{1·2\cdots p} \left(1 - \frac{1}{n}\right) \left(1 - \frac{2}{n}\right)\cdots \left(1 - \frac{p - 1}{n}\right) \] は正であり、\(n\) の単調増加関数と分かる。項数は \(n\) と共に増えるので \(\left(1 + \dfrac{1}{n}\right)^{n}\) は \(n\) と共に増加し、\(n \to \infty\) のとき極限または \(+\infty\) に向かう。

しかし \[ \begin{aligned} \left(1 + \frac{1}{n}\right)^{n} & \lt 1 + 1 + \frac{1}{1·2} + \frac{1}{1·2·3} + \cdots + \frac{1}{1·2·3 \cdots n}\\ & \lt 1 + 1 + \frac{1}{2} + \frac{1}{2^{2}} + \cdots + \frac{1}{2^{n-1}} \lt 3 \end{aligned} \] が成り立つ。

よって \(\left(1 + \dfrac{1}{n}\right)^{n}\) は \(+\infty\) に向かわない。つまり \[ \lim_{n \to\infty} \left(1 + \frac{1}{n}\right)^{n} = e \] であり、\(e\) は \(2 \lt e \leq 3\) を満たす。

§74 補助的な不等式

以降で使うことになる初等的な不等式をいくつかここで示しておく。

1. \(\alpha \gt 1\) で \(r\) が正の整数なら \[ r\alpha^{r} \gt \alpha^{r-1} + \alpha^{r-2} + \cdots + 1 \] が成り立つ。両辺に \(\alpha - 1\) を乗じれば \[ r\alpha^{r}(\alpha - 1) \gt \alpha^{r} - 1 \] となり、さらに両辺に \(r(\alpha^{r} - 1)\) を足して \(r(r + 1)\) で割れば \[ \frac{\alpha^{r+1} - 1}{r + 1} \gt \frac{\alpha^{r} - 1}{r}\quad (\alpha \gt 1) \qquad \text{(1)} \] を得る。同様に \[ \frac{1 - \beta^{r+1}}{r + 1} \lt \frac{1 - \beta^{r}}{r}\quad (0 \lt \beta \lt 1) \qquad \text{(2)} \] も示せる。

   ここから \(r\) と \(s\) が正の整数で \(r \gt s\) なら \[ \frac{\alpha^{r} - 1}{r} \gt \frac{a^{s} - 1}{s},\quad \frac{1 - \beta^{r}}{r} \lt \frac{1 - \beta^{s}}{s} \qquad \text{(3)} \] が成り立つと分かる。ここで \(0 \lt \beta \lt 1 \lt \alpha\) である。特に \(s = 1\) とすれば \[ \alpha^{r} - 1 \gt r(\alpha - 1),\quad 1 - \beta^{r} \lt r(1 - \beta) \qquad \text{(4)} \] を得る。

2. 不等式 (3) と (4) は \(r\) と \(s\) が正の整数という仮定の下で証明したが、より一般的に \(r\) と \(s\) を正の有理数としても容易に示せる。例えば最初の不等式 (3) を示すには、\(a,\ b,\ c,\ d\) を正の整数として \(r = a/b,\ s = c/d\) とおく。このとき \(ad \gt bc\) で、\(\alpha = \gamma^{bd}\) とおけば示すべき不等式は \[ \frac{\gamma^{ad} - 1}{ad} \gt \frac{\gamma^{bc} - 1}{bc} \] となるが、これは既に示されている。同じ議論は不等式 (4) にも適用できる。また \[ \alpha^{s} - 1 \lt s(\alpha - 1),\quad 1 - \beta^{s} \gt s(1 - \beta) \qquad \text{(5)} \] も同様に示せる。

3. これからは全ての記号が正の数を表し、\(r\) と \(s\) は有理数で、\(\alpha\) と \(r\) は \(1\) より大きく、\(\beta\) と \(s\) は \(1\) より小さいとする。(4) で \(\alpha\) に \(1/\beta\) を代入し、\(\beta\) に \(1/\alpha\) を代入すると \[ \alpha^{r} - 1 \lt r\alpha^{r-1}(\alpha - 1),\quad 1 - \beta^{r} \gt r\beta^{r-1}(1 - \beta) \qquad \text{(6)} \] を得る。同様に (5) からは \[ \alpha^{s} - 1 \gt s\alpha^{s-1}(\alpha - 1),\quad 1 - \beta^{s} \lt s\beta^{s-1}(1 - \beta) \qquad \text{(7)} \] が分かる。

   (4) と (6) を合わせると \[ r\alpha^{r-1}(\alpha - 1) \gt \alpha^{r} - 1 \gt r(\alpha - 1) \qquad \text{(8)} \] となり、\(\alpha\) に \(x/y\) を代入すると \[ rx^{r-1} (x - y) \gt x^{r} - y^{r} \gt ry^{r-1} (x - y) \qquad \text{(9)} \] が得られる。ただし \(x \gt y \gt 0\) である。同様に (5) と (7) からは \[ sx^{s-1} (x - y) \lt x^{s} - y^{s} \lt sy^{s-1} (x - y) \qquad \text{(10)} \] が分かる。

§75 \(n (\sqrt[n]{x} - 1)\) の極限

§74 の不等式 (3) の最初の式に \(r = 1/(n-1)\) と \(s = 1/n\) を代入すると、\(\alpha \gt 1\) なら \[ (n - 1)(\sqrt[n-1]{\alpha} - 1) \gt n(\sqrt[n]{\alpha} - 1) \] だと分かる。よって \(\phi(n) = n(\sqrt[n]{\alpha} - 1)\) なら \(\phi(n)\) は \(n\) に関して単調減少する。加えて \(\phi(n)\) は常に正なので、\(\phi(n)\) は \(n \to \infty\) のとき極限 \(l\) に向かい、\(l \geq 0\) である。

同様に §74 で示した (7) の最初の式で \(s = 1/n\) とすると \[ n(\sqrt[n]{\alpha} - 1) \gt \sqrt[n]{\alpha}\left(1 - \frac{1}{\alpha}\right) \gt 1 - \frac{1}{\alpha} \] を得る。よって \(l \geq 1 - (1/\alpha) \gt 0\) が分かる。つまり \(\alpha \gt 1\) なら \[ \lim_{n \to \infty} n(\sqrt[n]{\alpha} - 1) = f(\alpha) \] であり、\(f(\alpha) \gt 0\) が成り立つ。

次に \(\beta \lt 1\) として \(\beta = 1/\alpha\) と置けば、\(n(\sqrt[n]{\beta} - 1) = -n(\sqrt[n]{\alpha} - 1)/\sqrt[n]{\alpha}\) が成り立つ。\(n(\sqrt[n]{\alpha} - 1) \to f(\alpha)\) であり、例 27.10 から \[ \sqrt[n]{\alpha} \to 1 \] なので、\(\beta = 1/\alpha \lt 1\) なら \[ n(\sqrt[n]{\beta} - 1) \to -f(\alpha) \] が分かる。最後に \(x = 1\) なら全ての \(n\) に対して \(n(\sqrt[n]{x} - 1) = 0\) が成り立つ。

以上より、次の結果が得られる: 極限 \[ \lim n(\sqrt[n]{x} - 1) \] は全ての正の \(x\) に対して定義される \(x\) の関数を定義する。この関数 \(f(x)\) は \[ f(1/x) = -f(x),\quad f(1) = 0 \] を満たし、\(x \gt 1\) なら正、\(x \lt 1\) なら負である。\(x\) のネイピアの対数 (Napierian logarithm) を使ったこの関数の特徴付けを後で説明する。

例 \(f(xy) = f(x) + f(y)\) を示せ。 [等式 \[ f(xy) = \lim n(\sqrt[n]{xy} - 1) = \lim \{n(\sqrt[n]{x} - 1)\sqrt[n]{y} + n(\sqrt[n]{y} - 1)\} \] を使う]

§76 無限級数

\(u(n)\) が \(n\) の関数で、全ての \(n\) に対して定義されているとする。\(\nu = 1,\ 2,\ \ldots,\ n\) に対応する \(u(\nu)\) の値を全て足せば、\(u(\nu)\) とは異なる \(n\) の関数が得られる。具体的には \[ s(n) = u(1) + u(2) + \cdots + u(n) \] であり、この関数も全ての \(n\) に対して定義される。簡便のために、記法を少し変えて \[ s_{n} = u_{1} + u_{2} + \cdots + u_{n} \] あるいは \[ s_{n} = \sum_{\nu=1}^{n} u_{\nu} \] と書くことが多い。

\(n\) が \(\infty\) に向かうときに \(s_{n}\) が極限 \(s\) に向かうなら \[ \lim_{n\to\infty} \sum_{\nu=1}^{n} u_{\nu} = s \] となる。この等式を通常 \[ \sum_{\nu=1}^{\infty} u_{\nu} = s, \quad u_{1} + u_{2} + u_{3} + \cdots = s \] と書く。点々 \(\cdots\) は \(u\) の級数が無限に続くことを表す。

この等式は、\(u\) を最初からたくさん足していくと足すたびに和が極限 \(s\) に近づくことを意味する。より正確に言えば、任意に小さい正の数 \(\varepsilon\) について、最初の \(n_{0}(\varepsilon)\) 項 (および \(n_{0}(\varepsilon)\) より多い項) の和が \(s - \varepsilon\) と \(s + \varepsilon\) の間にあるように \(n_{0}(\varepsilon)\) を選べることを意味する。前に定義した記号を使えば、\(n \geq n_{0}(\varepsilon)\) のとき \[ s - \varepsilon \lt s_{n} \lt s + \varepsilon \] である。こういった状況において、級数 \[ u_{1} + u_{2} + \cdots \] を収束する無限級数 (convergent infinite series) と呼び、\(s\) を級数の和 (sum) あるいは級数の全項の和 (sum of all the terms) と呼ぶ。

つまり級数 \(u_{1} + u_{2} + \cdots\) が「収束して和が \(s\)となる」「和 \(s\) に収束する」「\(s\) に収束する」と言ったとしても、それは最初の \(n\) 項の和 \(s_{n} = u_{1} + u_{2} + \cdots + u_{n}\) が \(n \to \infty\) のとき極限 \(s\) に向かうことを別の表現で表しているに過ぎない。無限級数を考えたとしてもこれまでに扱っていない概念は必要とならないので、読者はすぐに理解できるはずである。実際、和 \(s_{n}\) は今まで考えてきた関数 \(\phi(n)\) の表記を変えただけであり、任意の関数 \(\phi(n)\) は次のようにして級数の形に表せる: \[ \phi(n) = \phi(1) + \{\phi(2) - \phi(1)\} + \cdots + \{\phi(n) - \phi(n - 1)\} \] \(\phi(n)\) は \(n \to \infty\) のとき \(l\) に「収束する」と言った方が (「向かう」と言うよりも) 分かりやすい場合もある。

\(s_{n} \to +\infty\) または \(s_{n} \to -\infty\) のとき、級数 \(u_{1} + u_{2} + \cdots\) は発散する (divergent) あるいは \(\bm{ +\infty}\) に発散する (diverges to \( +\infty\)) および \(\bm{ -\infty}\) に発散する (diverges to \( -\infty\)) と言う。例えば「\(\phi(n)\) は \( +\infty\) に発散する」は \(\phi(n) \to +\infty\) を意味する。\(s_{n}\) が極限にも \( +\infty\) にも \(-\infty\) にも向かわないなら、\(s_{n}\) は有限または無限に振動する。このとき級数 \(u_{1} + u_{2} + \cdots\) は有限または無限に振動すると言う⁸。

§77 無限級数に関する定理

これから無限級数を扱うときには、次の一般的な定理を利用できる場面に多く遭遇する:

1. \(u_{1} + u_{2} + \cdots\) が収束して和が \(s\) なら、\(a + u_{1} + u_{2} + \cdots\) は収束して和は \(a + s\) となる。同様に \(a + b + c + \cdots + k + u_{1} + u_{2} + \cdots\) は収束して和は \(a + b + c + \cdots + k + s\) となる。

2. \(u_{1} + u_{2} + \cdots\) が収束して和が \(s\) なら、\(u_{m+1} + u_{m+2} + \cdots\) は収束して和は \[ s - u_{1} - u_{2} - \cdots - u_{m} \] となる。

3. (1) および (2) で最初の級数が発散もしくは振動するなら、後の級数も同じ振る舞いをする。

4. \(u_{1} + u_{2} + \cdots\) が収束して和が \(s\) なら、\(ku_{1} + ku_{2} + \cdots\) は収束して和は \(ks\) となる。

5. (4) で最初の級数が発散もしくは振動するなら、\(k = 0\) でない限り後の級数も同じ振る舞いをする。

6. \(u_{1} + u_{2} + \cdots\) と \(v_{1} + v_{2} + \cdots\) がどちらも収束するなら級数 \((u_{1} + v_{1}) + (u_{2} + v_{2}) + \cdots\) も収束し、和は元の二つの級数の和を足したものに等しい。

以上の定理は全て、収束の定義や §63–§66 の結果を和 \(s_{n} = u_{1} + u_{2} + \cdots + u_{n}\) に適用すれば得られる。次の定理は異なる特徴を持つ:

7. \(u_{1} + u_{2} + \cdots\) が収束するなら \(\lim u_{n} = 0\) が成り立つ。

   この定理の逆も正しく、\(\lim u_{n} = 0\) なら級数 \(\sum u_{n}\) も収束するだろうと思うかもしれない。しかし簡単な例を使えばこれが正しくないと示せる。級数 \[ 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \cdots \] では \(u_{n} = 1/n\) であり、最初の四項の和は \[ 1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} \gt 1 + \frac{1}{2} + \frac{2}{4} = 1 + \frac{1}{2} + \frac{1}{2} \] を満たす。次の四つの項の和では \(\frac{1}{5} + \frac{1}{6} + \frac{1}{7} + \frac{1}{8} \gt \frac{4}{8} = \frac{1}{2}\) であり、その次の八項の和も \(\frac{8}{16} = \frac{1}{2}\) より大きい。以降同様なので、最初の \[ 4 + 4 + 8 + 16 + \cdots + 2^{n} = 2^{n+1} \] 項の和が \[ 2 + \frac{1}{2} + \frac{1}{2} + \frac{1}{2} + \cdots + \frac{1}{2} = \frac{1}{2} (n + 3) \] より大きいと示せる。これは \(n\) と共にいくらでも大きくなるので、級数は \(+\infty\) に発散する。

8. \(u_{1} + u_{2} + u_{3} + \cdots\) が収束するなら、この級数の項を括弧でくくってできる任意の級数も収束し、和は元の級数と等しい。

   この定理の証明は読者に任せる。なおここでも逆は正しくない。例えば \(1 - 1 + 1 - 1 + \cdots\) は振動するが、 \[ (1 - 1) + (1 - 1) + \cdots \] つまり \(0 + 0 + 0 + \cdots\) は \(0\) に収束する。

9. 全ての \(u_{n}\) が正または \(0\) なら、\(\sum u_{n}\) は収束するか、そうでなければ \(+\infty\) に発散する。そして収束するなら和は正である (全ての項が \(0\) の場合は除く。この場合の和はもちろん \(0\) となる)。

   \(s_{n}\) は §69 の意味で \(n\) の増加関数だから、この節の結果を \(s_{n}\) に適用できる。

10. 全ての項 \(u_{n}\) が正または \(0\) とする。\(\sum u_{n}\) が収束するための必要十分条件は、任意個の項の和が \(K\) 以下となるような実数 \(K\) を見つけられることである。そのとき級数の和は \(K\) 以下となる。

    これも §69 の定理から直ちに従う。言うまでもなく \(u_{n}\) が全て正であるという条件が満たされないならこの結果は成り立たない。例えば \[ 1 - 1 + 1 - 1 + \cdots \] は振動するが、\(s_{n}\) は \(1\) と \(0\) を交互に取る。

11. 二つの級数 \(u_{1} + u_{2} + \cdots\) と \(v_{1} + v_{2} + \cdots\) の項が全て正または \(0\) だとする。ある定数 \(K\) に対して全ての \(n\) で \(u_{n} \leq Kv_{n}\) なら、二つ目の級数が収束するとき最初の級数も収束する。そのとき最初の級数の和は二番目の級数の和の \(K\) 倍以下となる。

    \(v_{1} + v_{2} + \cdots = t\) なら全ての \(n\) に対して \(v_{1} + v_{2} + \cdots + v_{n} \leq t\) であり、ここから \(u_{1} + u_{2} + \cdots + u_{n} \leq Kt\) となって定理が証明できる。

    逆に \(\sum u_{n}\) が発散して \(v_{n} \geq Ku_{n}\) なら \(\sum v_{n}\) も発散する。

§78 無限幾何級数

続いて "幾何" 級数 (geometrical series) を考える。この級数の一般項は \(u_{n} = r^{n-1}\) で \[ s_{n} = 1 + r + r^{2} + \cdots + r^{n-1} = \frac{1 - r^{n}}{1 - r} \] が成り立つ。ただし \(r = 1\) のときは例外で \[ s_{n} = 1 + 1 + \cdots + 1 = n \] となる。\(r = 1\) なら \(s_{n} \to \infty\) だが、一般に \(s_{n}\) は \(r^{n}\) が極限に向かうときに限って収束する。§72 の結果を使えば次が分かる:

もし \(r \geq 1\) なら \(s_{n} \geq n\) であり \(s_{n} \to +\infty\)、すなわち級数は \( +\infty\) に発散する。もし \(r = -1\) なら \(n\) が奇数のとき \(s_{n} = 1\) でそうでないとき \(s_{n} = 0\) となる、つまり \(s_{n}\) は有限に振動する。そして \(r \lt -1\) なら \(s_{n}\) は無限に振動する。以上の結果を次にまとめる:

§79 極限を使った連続実関数の表現

ここまでの節で \[ \lim_{n \to \infty} \phi_{n}(x) \] という形の関数の極限、あるいは \[ u_{1}(x) + u_{2}(x) + \cdots = \lim_{n \to \infty}\{u_{1}(x) + u_{2}(x) + \cdots + u_{n}(x)\} \] という形の級数を考えた。こういった関数や級数は \(n\) の関数だが、その極限には \(n\) 以外に \(x\) というもう一つの変数が関係しており、極限は \(x\) の関数となる。例えば §75 では \[ f(x) = \lim_{n \to \infty} n(\sqrt[n]{x} - 1) \] という形の関数を考えた。あるいは幾何級数 \(1 + x + x^{2} + \cdots\) は \(x\) の関数であり、\(-1 \lt x \lt 1\) なら \(1/(1 - x)\) に等しく、それ以外では全ての \(x\) に対して定義されない。

第三章で登場した一見すると "無理やり作ったように見える" "不自然な" 関数は、極限を使うと簡単に表現できる。次の例を見ればこのことを理解できるだろう。

§80 有界集合の上限と下限

\(S\) を実数の集合とする。\(S\) に含まれる全ての \(s\) について \(s \leq K\) となる実数 \(K\) が存在するなら、\(S\) は上に有界 (bounded above) と言う。全ての \(s\) について \(s \geq K\) となる実数 \(K\) が存在するなら、\(S\) は下に有界 (bounded below) と言う。\(S\) が下にも上にも有界なら、\(S\) は有界 (bounded) と言う。

\(S\) が上に有界だとする (下に有界でなくてもよい)。このとき上述の \(K\) が持つ「全ての \(s\) に対して \(s \leq K\)」という性質を持つ実数は \(K\) の他にも無限にある。例えば \(K\) より大きい全ての数はこの性質を持つ。これからこの性質を持つ実数に最小値 \(\bm{M}\) があることを示す¹²。この \(M\) より大きい \(S\) の任意は存在せず、それでいて \(M\) より小さい任意の実数は少なくとも一つの \(S\) の要素より小さくなる。

実数 \(\xi\) を次のようにして二つのクラス \(L\) と \(R\) に分ける。\(\xi\) より大きい要素が \(S\) にあるなら \(\xi\) を \(L\) 入れ、そうでないなら \(R\) に入れる。すると全ての \(\xi\) は \(L\) と \(R\) のどちらかに含まれる。また \(S\) のいずれかの要素より小さい数は \(L\) に含まれ \(K\) は \(R\) に含まれるので、両方のクラスは一つ以上の要素を持つ。そして \(L\) の任意の要素は \(S\) のいずれかの要素より小さく、したがって \(R\) の任意の要素より小さい。よってデデキントの定理 (§17) の三つの条件が成り立つので、二つのクラスを分ける実数 \(M\) が存在する。

この \(M\) こそが存在を証明しようとしていた実数である。まず、\(M\) は \(S\) の任意の要素より大きい: もし \(S\) のとある要素 \(s\) が \(M\) より大きかったとすると、正の実数 \(\eta\) を使って \(s = M + \eta\) と書ける。すると \(M + \frac{1}{2}\eta\) は \(s\) より小さいので \(L\) に含まれ、\(M\) より大きいので \(R\) にも含まれることになるが、これはあり得ない。一方で \(M\) より小さい任意の数は \(L\) に含まれ、したがって少なくとも一つの \(S\) の要素より小さい。以上より、\(M\) は必要とされる性質を全て持つ。

この数 \(M\) を \(S\) の上限 (supremum) と呼ぶ¹³。今示した事実を次にまとめる:

同様に (上に有界だとは限らない) 下に有界な集合に対する定理も示せる:

\(S\) が上に有界なら \(M \leq K\) が成り立ち、\(S\) が下に有界なら \(m \geq k\) が成り立つ。よって \(S\) が有界なら \(k \leq m \leq M \leq K\) となる。

§81 有界関数の上限と下限

\(\phi(n)\) を正整数変数 \(n\) の関数とする。\(\phi(n)\) の値を全て集めると集合 \(S\) が定義でき、\(S\) に対しては §80 の議論を全て適用できる。こうして定義される \(S\) が上に有界、下に有界、有界のとき、\(\phi(n)\) をそれぞれ上に有界、下に有界、有界と言う。\(\phi(n)\) が上に有界なら、ある実数 \(K\) が存在して全ての \(n\) に対して \(\phi(n) \leq K\) となる。このときある実数 \(M\) があって

• 全ての \(n\) に対して \(\phi(n) \leq M\)
• 任意の正の実数 \(\varepsilon\) に対して、少なくとも一つの \(n\) で \(\phi(n) \gt M - \varepsilon\)

が成り立つ。この実数 \(M\) を \(\phi(n)\) の上限 (supremum) と呼ぶ。同様に \(\phi(n)\) が下に有界なら、ある実数が \(k\) があって全ての \(n\) で \(\phi(n) \geq k\) である。このときある実数 \(m\) があって

• 全ての \(n\) に対して \(\phi(n) \geq m\)
• 任意の正の実数 \(\varepsilon\) に対して、少なくとも一つの \(n\) で \(\phi(n) \lt m + \varepsilon\)

が成り立つ。この実数 \(m\) を \(\phi(n)\) の下限 (infimum) と呼ぶ。

\(K\) が存在するなら \(M \leq K\) が成り立ち、\(k\) が存在するなら \(m \geq k\) が成り立つ。そして \(k\) と \(K\) が両方存在するなら次の不等式が成り立つ: \[ k \leq m \leq M \leq K \]

§82 上極限と下極限

\(\phi(n)\) を有界関数、\(M\) と \(m\) を \(\phi(n)\) の上限と下限とする。任意の実数 \(\xi\) を取り、大きい \(n\) に対する \(\phi(n)\) と \(\xi\) の間で成り立つ不等式について考える。可能性は三つあり、どれか一つだけが起こる:

1. 十分大きい全ての \(n\) で \(\xi \geq \phi(n)\)
2. 十分大きい全ての \(n\) で \(\xi \leq \phi(n)\)
3. 無限個の \(n\) で \(\xi \lt \phi(n)\)、かつ無限個の \(n\) で \(\xi \gt \phi(n)\)

(1) のとき \(\xi\) を上の数 (superior number) と呼び、(2) のとき \(\xi\) を下の数 (inferior number)、(3) のとき \(\xi\) を中間の数 (intermediate number) と呼ぶ。明らかに、上の数は \(m\) および下の数より小さくならない。

上の数全体の集合を考える。要素が全て \(m\) 以上であるこの集合は下に有界であり、下限 \(\Lambda\) を持つ。同様に下の数を集めた集合は上限 \(\lambda\) を持つ。

\(\Lambda\) と \(\lambda\) を \(n\) が無限大に向かうときの \(\phi(n)\) の 上極限 (upper limit) および 下極限 (lower limit) と呼び¹⁴、次のように書く: \[ \Lambda = \limsup \phi(n),\quad \lambda = \liminf \phi(n) \] 上極限と下極限は次の性質を持つ:

1. \(m \leq \lambda \leq \Lambda \leq M\)
2. 中間の数の集合に要素が存在するなら、\(\Lambda\) と \(\lambda\) が中間の数の上限および下限となる。
3. \(\varepsilon\) を任意の正の実数とすると、十分大きい全ての \(n\) に対して \(\phi(n) \lt \Lambda + \varepsilon\) および無限個の \(n\) に対して \(\phi(n) \gt \Lambda - \varepsilon\) が成り立つ。
4. 同様に十分大きい全ての \(n\) に対して \(\phi(n) \gt \lambda - \varepsilon\) および無限個の \(n\) に対して \(\phi(n) \lt \lambda + \varepsilon\) が成り立つ。
5. \(\phi(n)\) が極限に向かうための必要十分条件は \(\Lambda = \lambda\) である。これが成り立つなら、\(\phi(n)\) は極限 \(l = \Lambda = \lambda\) に向かう。

これらの性質の中で (1) は定義から直ちに従う。(2) は次のように示せる。もし \(\Lambda = \lambda = l\) なら中間の値は唯一 \(l\) だけであり、性質は明らかに成り立つ。そうでなくて \(\Lambda \gt \lambda\) なら、任意の中間の数 \(\xi\) は上の数より小さく下の数より大きく \(\lambda \leq \xi \leq \Lambda\) となる。そしてもし \(\lambda \lt \xi \lt \Lambda\) なら \(\xi\) は上の数でも下の数でもないので、中間の数となる。よって \(\lambda\) と \(\Lambda\) に好きなだけ近い \(\xi\) が存在する。

(3) を示すには、\(\Lambda + \varepsilon\) が上の数で \(\Lambda - \varepsilon\) が中間の数または下の数なことを利用する。これと定義を使えばすぐに示せる。(4) の証明も同様にできる。

(5) は次のように証明できる。\(\Lambda = \lambda = l\) なら \[ l - \varepsilon \lt \phi(n) \lt l + \varepsilon \] が任意の正の実数 \(\varepsilon\) と十分大きな全ての \(n\) に対して成り立つので、\(\phi(n) \to l\) と分かる。逆に \(\phi(n) \to n\) なら上の不等式が十分大きな全ての \(n\) で成り立つので、\(l - \varepsilon\) は下の数で \(l + \varepsilon\) は上の数となる。よって \[ \lambda \geq l - \varepsilon,\quad \Lambda \leq l + \varepsilon \] すなわち \(\Lambda - \lambda \leq 2\varepsilon\) であり、\(\Lambda - \lambda \geq 0\) よりこれは \(\Lambda = \lambda\) のときに限って正しい。

§83 有界関数に対する収束の基本原則 (コーシーの収束判定法)

前節の結果から \(\phi(n)\) が極限に向かうための必要十分条件が分かる。これは「収束の基本原則¹⁶ (the general principle of convergence)」と呼ばれる非常に重要な条件である。

まず必要性を示す。\(\phi(n) \to l\) のときある \(n_{0}\) があって \(n \geq n_{0}\) で \[ l - \frac{1}{2}\varepsilon \lt \phi(n) \lt l + \frac{1}{2}\varepsilon \] が成り立つ。よって全ての \(n_{1} \geq n_{0}\) と全ての \(n_{2} \geq n_{0}\) で \[ |\phi(n_{2}) - \phi(n_{1})| \lt \varepsilon \qquad \text{(1)} \] となる。

次に十分性を示す。\(\lambda = \Lambda\) を示せばよい。もし \(\lambda \lt \Lambda\) なら、どれだけ小さい正の \(\varepsilon\) に対しても、無限個の \(n\) で \(\phi(n) \lt \lambda + \varepsilon\) および無限個の \(n\) で \(\phi(n) \gt \Lambda - \varepsilon\) となる。よって与えられた任意の \(n_{0}\) より大きい \(n_{1}\) と \(n_{2}\) であって \[ \phi(n_{2}) - \phi(n_{1}) \gt \Lambda - \lambda - 2\varepsilon \] が成り立つものを取れる。\(\varepsilon\) が十分小さいときこれは \(\frac{1}{2}(\Lambda - \lambda)\) より大きくなるが、これは (1) と矛盾する。よって \(\lambda = \Lambda\) であり、\(\phi(n)\) は極限に向かう。

§84 非有界関数

ここまでは有界関数だけを考えてきた。しかし次に示すように「収束の基本原則」は関数の有界性を仮定しなくても成り立つので、前節で示した定理からは「有界関数」という言葉を取り除ける。

まず \(\phi(n)\) が極限 \(l\) に向かうなら、有限個の値を除いた全ての値が \(l + \varepsilon\) と \(l - \varepsilon\) と \(\phi(n)\) の間にあるので、\(\phi(n)\) が有界だと分かる。

次に前節の定理の条件が満たされるなら、 \[ |\phi(n_{2}) - \phi(n_{1})| \lt \varepsilon \] が全ての \(n_{1} \geq n_{0}\) と全ての \(n_{2} \geq n_{0}\) で成り立つ。\(n_{0}\) より大きい \(n_{1}\) を固定すれば \[ \phi(n_{1}) - \varepsilon \lt \phi(n_{2}) \lt \phi(n_{1}) + \varepsilon \] が \(n_{2} \geq n_{0}\) のとき成り立つ。ここから \(\phi(n)\) は有界と分かり、前節で示した証明の後半部分が適用できる。

この「収束の基本原則」の理論的重要性はどれだけ強調しても強調しすぎることはない。§69 の定理と同じように、この条件を使うと \(\phi(n)\) が極限を持つかどうかを極限の値を求めずに判定できる。さらに §69 の定理が持っていた単調増加という特殊な仮定をこの条件は持っていない。ただ簡単な問題ではこの条件が必要とならず、単調増加の仮定が付いた定理を使えば示したいことを示せる場合が多い。この条件は非常に重要であるものの、以降の章でこの条件が使われることは実質一度もない¹⁷。ここでは次の点を指摘するに留める: \[ \phi(n) = s_{n} = u_{1} + u_{2} + \cdots + u_{n} \] とすれば、無限級数の収束性に関する必要十分条件が直ちに得られる:

§85 複素関数と複素級数の極限

この章ではこれまで \(n\) の実関数と項が実数の級数を考えてきた。こういった概念と定義は関数の値や級数の項が複素数の場合へと自然に拡張できる。

\(\phi(n)\) が複素数 \[ \rho(n) + i\sigma(n) \] で、\(\rho(n)\) と \(\sigma(n)\) が \(n\) の実関数だとする。このとき \(\rho(n)\) と \(\sigma(n)\) が \(n \to \infty\) のときにそれぞれ極限 \(r\) と \(s\) に向かうなら \(\phi(n)\) は極限 \(l = r + is\) に収束すると言い、 \[ \lim\phi(n) = l \] と書く。同様に \(u_{n}\) が複素数 \(v_{n} + iw_{n}\) なら、級数 \[ u_{1} + u_{2} + u_{3} + \cdots \] が和 \(l = r + is\) に収束するのは、級数 \[ v_{1} + v_{2} + v_{3} + \cdots,\quad w_{1} + w_{2} + w_{3} + \cdots \] がそれぞれ \(r,\ s\) に収束するときである。

\(u_{1} + u_{2} + u_{3} + \cdots\) が和 \(l\) に収束するといった場合、もちろんそれは和 \[ s_{n} = u_{1} + u_{2} + \cdots + u_{n} = (v_{1} + v_{2} + \cdots + v_{n}) + i(w_{1} + w_{2} + \cdots + w_{n}) \] が \(n \to \infty\) で \(l\) に収束することを表す。

実関数と実級数では収束に他にも発散と有限および無限の振動を定義した。しかし複素関数と複素級数では \(\rho(n)\) と \(\sigma(n)\) の両方を考えなければならず細かな場合分けが多く生じるので、定義する意味がほとんどない。そこで収束しない複素関数と複素級数をさらに細かく区別する必要がある場合には、実部と虚部の振る舞いに関する議論を別々に行うことにする。

§86 複素関数と複素級数の特徴

次の定理は実関数や実級数に関して証明したものと同様であり、証明は難しくない。

1. \(\lim\phi(n) = l\) なら固定された任意の \(p\) に対して \(\lim\phi(n + p) = l\) となる。

2. \(u_{1} + u_{2} + \cdots\) が収束して和が \(l\) なら \(a + b + c + \cdots + k + u_{1} + u_{2} + \cdots\) は和 \(a + b + c + \cdots + k + l\) に収束し、\(u_{p+1} + u_{p+2} + \cdots\) は和 \(l - u_{1} - u_{2} - \cdots - u_{p}\) に収束する。

3. \(\lim\phi(n) = l\) かつ \(\lim\psi(n) = m\) なら \[ \lim\{\phi(n) + \psi(n)\} = l + m \] が成り立つ。

4. \(\lim\phi(n) = l\) なら \(\lim k\phi(n) = kl\) となる。

5. \(\lim\phi(n) = l\) かつ \(\lim\psi(n) = m\) なら \(\lim \phi(n)\psi(n) = lm\) となる。

6. \(u_{1} + u_{2} + \cdots\) が和 \(l\) に収束し \(v_{1} + v_{2} + \cdots\) が和 \(m\) に収束するなら、\((u_{1} + v_{1}) + (u_{2}+ v_{2}) + \cdots\) は和 \(l + m\) に収束する。

7. \(u_{1} + u_{2} + \cdots\) が和 \(l\) に収束するなら、\(ku_{1} + ku_{2} + \cdots\) は和 \(kl\) に収束する。

8. \(u_{1} + u_{2} + u_{3} + \cdots\) が収束するなら \(\lim u_{n} = 0\) となる。

9. \(u_{1} + u_{2} + u_{3} + \cdots\) が収束するなら、この級数の項に適当に括弧を付けてできる新しい級数も全て収束し、そういった級数と元の級数の和は等しい。

   例として (5) を示す。 \[ \begin{gathered} \phi(n) = \rho(n) + i\sigma(n), \quad \psi(n) = \rho'(n) + i\sigma'(n), \\ l = r + is, \quad m = r' + is' \end{gathered} \] とする。

   このとき \[ \begin{gathered} \rho(n) \to r,\quad \sigma(n) \to s,\\ \rho'(n) \to r',\quad \sigma'(n) \to s' \end{gathered} \] が成り立つ。

   ここで \[ \phi(n)\psi(n) = \rho\rho' - \sigma\sigma' + i(\rho\sigma' + \rho'\sigma) \] および \[ \begin{aligned} \rho\rho' - \sigma\sigma' & \to rr' - ss',\\ \rho\sigma' + \rho'\sigma & \to rs' + r's \end{aligned} \] であり、ここから \[ \phi(n)\psi(n) \to rr' - ss' + i(rs' + r's) \] つまり \[ \phi(n)\psi(n) \to (r + is)(r' + is') = lm \] が分かる。

次の定理は少し異なる特徴を持つ:

10. \(n \to \infty\) で \(\phi(n) = \rho(n) + i\sigma(n)\) が \(0\) に収束するための必要十分条件は \[ |\phi(n)| = \sqrt{\{\rho(n)\}^{2} + \{\sigma(n)\}^{2}} \] が \(0\) に収束することである。

    \(\rho(n)\) と \(\sigma(n)\) が \(0\) が収束するなら、明らかに \(\sqrt{\rho^{2} + \sigma^{2}}\) も \(0\) に収束する。逆は \(\rho\) と \(\sigma\) の絶対値が \(\sqrt{\rho^{2} + \sigma^{2}}\) 以下なことから従う。

11. より一般的に言うと、\(\phi(n)\) が極限 \(l\) に収束するための必要十分条件は \[ |\phi(n) - l| \] が \(0\) に収束することである。

    \(\phi(n) - l\) が \(0\) に収束するので、(10) を適用できる。

12. §83–§84 の定理は \(\phi(n)\) と \(u_{n}\) が複素数であっても成り立つ。

    \(\phi(n)\) が \(l\) に収束するための必要十分条件が、\(n_{2} \gt n_{1} \geq n_{0}\) に対して \[ |\phi(n_{2}) - \phi(n_{1})| \lt \varepsilon \qquad \text{(1)} \] だと示せばよい。

    \(\phi(n) \to l\) なら \(\rho(n) \to r\) かつ \(\sigma(n) \to s\) であり、\(\varepsilon\) に対応する \(n_{0}'\) と \(n_{0}''\) があって \[ \begin{aligned} |\rho(n_{2}) - \rho(n_{1})| & \lt \frac{1}{2}\varepsilon,\\ |\sigma(n_{2}) - \sigma(n_{1})| & \lt \frac{1}{2}\varepsilon \end{aligned} \] がそれぞれ \(n_{2} \gt n_{1} \geq n_{0}'\) と \(n_{2} \gt n_{1} \geq n_{0}''\) のとき成り立つ。よって \(n_{0}'\) と \(n_{0}''\) の大きい方を \(n_{0}\) とすれば \[ |\phi(n_{2}) - \phi(n_{1})| \leq |\rho(n_{2}) - \rho(n_{1})| + |\sigma(n_{2}) - \sigma(n_{1})| \lt \varepsilon \] が \(n_{2} \gt n_{1} \geq n_{0}\) のとき成り立つ。よって条件 (1) は必要である。十分性は次のように示す。\(n_{2} \gt n_{1} \geq n_{0}\) のとき \[ |\rho(n_{2}) - \rho(n_{1})| \leq |\phi(n_{2}) - \phi(n_{1})| \lt \varepsilon \] だから、\(\rho(n)\) は極限 \(r\) に向かうと分かる。同様に \(\sigma(n)\) が \(s\) に向かうことも分かる。

§87 複素数 \(z\) に対する \(z^{n}\) の極限

\(\phi(n) = z^{n}\) という重要なケースを考える。\(z\) が実数の場合のこの問題は前に §72 で考えた。

§86 の (1) より \(z^{n} \to l\) なら \(z^{n+1} \to l\) となる。一方 §86 の (4) からは \[ z^{n+1} = zz^{n} \to zl \] が分かるので、\(l = zl\) が成り立つ。これは (a) \(l = 0\) または (b) \(z = 1\) のときに限って成り立つ。\(z = 1\) なら \(\lim z^{n} = 1\) である。この特殊ケースを除けば、極限が存在するならそれは \(0\) となる。

正の \(r\) を使って \(z = r(\cos\theta + i\sin\theta)\) とする。このとき \[ z^{n} = r^{n} (\cos n\theta + i\sin n\theta) \] だから、\(|z^{n}| = r^{n}\) が成り立つ。よって \(|z^{n}|\) は \(r \lt 1\) のときに限って \(0\) に向かう。よって §86 の (10) から \[ \lim z^{n} = 0 \] が \(r \lt 1\) のときに限って成り立つと分かる。これ以外のとき \(z^{n}\) は収束しない。唯一の例外は \(z = 1\) で、このときは \(z^{n} \to 1\) となる。

§88 複素数 \(z\) の幾何級数

\(z \neq 1\) なら等式 \[ s_{n} = 1 + z + z^{2} + \cdots + z^{n-1} = \frac{1 - z^{n}}{1 - z} \] が成り立つので、級数 \(\bm{1 + z + z^{2} + \cdots}\) が収束するのは \(\bm{r = |z| \lt 1}\) のときに限る。そのときの和は \(1/(1 - z)\) となる。

よって \(z = r(\cos\theta + i\sin\theta) = r\operatorname{Cis}\theta\) で \(r \lt 1\) なら \[ \begin{aligned} 1 + z + z^{2} + \cdots & = \frac{1}{1 - r\operatorname{Cis}\theta} \\ \end{aligned} \] つまり \[ \begin{aligned} 1 + r \operatorname{Cis}\theta + r^{2} \operatorname{Cis} 2\theta + \cdots & = \frac{1}{1 - r\operatorname{Cis}\theta}\\ & = \frac{1 - r\cos\theta + ir\sin\theta}{1 - 2r\cos\theta + r^{2}} \end{aligned} \] となる。実部と虚部を分けて書けば、\(r \lt 1\) に対して \[ \begin{aligned} 1 + r\cos\theta + r^{2}\cos 2\theta + \cdots & = \frac{1 - r\cos\theta}{1 - 2r\cos\theta + r^{2}},\\ r\sin\theta + r^{2}\sin 2\theta + \cdots & = \frac{r\sin\theta}{1 - 2r\cos\theta + r^{2}} \end{aligned} \] を得る。\(\theta\) を \(\theta + \pi\) に変えれば、絶対値が \(1\) より小さい負の \(r\) でもこの式が成立すると分かる。つまりこの式は \(-1 \lt r \lt 1\) で成り立つ。

第四章のその他の例

1. 関数 \(\phi(n)\) が \(n = 0,\ 1,\ 2,\ \ldots\) で \(1,\ 0,\ 0,\ 0,\ 1,\ 0,\ 0,\ 0,\ 1,\ \ldots\) という値を取るとする。\(\phi(n)\) を三角関数が含まれない \(n\) の式で表せ。 [\(\phi(n) = \frac{1}{4}\{1 + (-1)^{n} + i^{n} + (-i)^{n}\}\)]

2. \(n\) が \(\infty\) に向かうとき \(\phi(n)\) が単調増加で \(\psi(n)\) が単調減少だとする。全ての \(n\) で \(\psi(n) \gt \phi(n)\) が成り立つなら、\(\phi(n)\) と \(\psi(n)\) の両方が極限に向かい、さらに \(\lim\phi(n) \leq \lim\psi(n)\) だと示せ。 [§69 の結果から直ちに得られる]

3. もし \[ \phi(n) = \left(1 + \frac{1}{n}\right)^{n},\quad \psi(n) = \left(1 - \frac{1}{n}\right)^{-n} \] なら \(\phi(n + 1) \gt \phi(n)\) かつ \(\psi(n + 1) \lt \psi(n)\) だと示せ。 [一つ目の式は §73 で示した]

4. 前問の設定で、全ての \(n\) に対して \(\psi(n) \gt \phi(n)\) だと示せ。そして \(n\) が \(\infty\) に向かうとき \(\phi(n)\) と \(\psi(n)\) が極限に向かうと (二つ前の問題を使って) 示せ¹⁸。

5. 和が \(n\) の正整数の組を全て考え、その積の代数平均を \(S_{n}\) とする。\(\lim(S_{n}/n^{2}) = 1/6\) を示せ。

   (Math. Trip. 1903.)

6. \(x\) と \(A\) が正で \(x_{1} = \frac{1}{2}\{x + (A/x)\},\ x_{2} = \frac{1}{2}\{x_{1} + (A/x_{1})\},\ \ldots\) という関係が成り立つなら \(\lim x_{n} = \sqrt{A}\) だと示せ。

   [まず \(\dfrac{x_{n} - \sqrt{A}}{x_{n} + \sqrt{A}} = \biggl(\dfrac{x - \sqrt{A}}{x + \sqrt{A}}\biggr)^{2^{n}}\) を示す]

7. 全ての \(n\) に対して \(\phi(n)\) が正の整数で、\(n\) と共に \(\infty\) に向かうとする。このとき \(x^{\phi(n)}\) は \(0 \lt x \lt 1\) なら \(0\) に向かい、\(x \gt 1\) なら \(+\infty\) に向かう。他の \(x\) の値に対する \(n \to \infty\) における \(x^{\phi(n)}\) の振る舞いを議論せよ。

8. \(n\) が増加するとき \(a_{n}\) が単調に増加または減少するなら、\((a_{1} + a_{2} + \cdots + a_{n})/n\) もそうだと示せ¹⁹。

9. \(x_{n+1} = \sqrt{k + x_{n}}\) で \(k\) と \(x_{1}\) は正とする。このとき \(x^{2} = x + k\) の正の根を \(\alpha\) とすると、\(x_{1}\) が \(\alpha\) より小さいとき \(x_{1},\ x_{2},\ x_{3},\ \ldots\) は増加列となり、そうでないとき減少列となる。いずれの場合でも \(n \to \infty\) のとき \(x_{n} \to \alpha\) が成り立つ。

10. \(x_{n+1} = k/(1 + x_{n})\) で \(k\) と \(x_{1}\) は正とする。このとき \(x_{1},\ x_{3},\ x_{5},\ \ldots\ \) と \(x_{2},\ x_{4},\ x_{6},\ \ldots\ \) は一方が増加列でもう一方が減少列となる。そして \(x^{2} = x + k\) の正の根を \(\alpha\) とすると、二つの列は両方とも極限 \(\alpha\) に向かう。

11. 関数 \(f(x)\) が単調増加かつ全ての \(x\) に対して連続 (第五章) で、列 \(x_{1},\ x_{2},\ x_{3},\ \ldots\ \) が \(x_{n+1} = f(x_{n})\) で定義されるとする。\(x_{n}\) が方程式 \(x = f(x)\) の根に向かうかどうかを、図を使って議論せよ。特にこの方程式が根を一つだけ持つケースについて、\(y = f(x)\) が上からおよび下から直線 \(y = x\) を横切るときにどうなるかを考えよ。

12. \(x_{1},\ x_{2}\) が正で \(x_{n+1} = \frac{1}{2} (x_{n} + x_{n-1})\) とする。このとき二つの数列 \(x_{1},\ x_{3},\ x_{5},\ \ldots\) と \(x_{2},\ x_{4},\ x_{6},\ \ldots\) は一方が減少列でもう一方で増加列となり、共通の極限 \(\frac{1}{3}(x_{1} + 2x_{2})\) を持つ。

13. 次の等式で定義される関数 \(y\) のグラフを描け。 \[ y = \lim_{n \to \infty} \frac{x^{2n} \sin\frac{1}{2}\pi x + x^{2}}{x^{2n} + 1} \]

    (Math. Trip. 1901)

14. 関数 \[ y = \lim_{n \to \infty} \frac{1}{1 + n\sin^{2} \pi x} \] は \(x\) が整数のとき \(1\) で、それ以外のとき \(0\) となる。関数 \[ y = \lim_{n \to \infty} \frac{\psi(x) + n\phi(x) \sin^{2}\pi x}{1 + n\sin^{2}\pi x} \] は \(x\) が整数のとき \(\psi(x)\) に等しく、それ以外のとき \(\phi(x)\) に等しい。

15. 関数 \[ y = \lim_{n \to \infty} \frac{x^{n}\phi(x) + x^{-n}\psi(x)}{x^{n} + x^{-n}} \] のグラフが \(\phi(x)\) と \(\psi(x)\) の一部分、および (一般には) 二つの孤立点からなると示せ。(a) \(x = 1\)、(b) \(x = -1\)、(c) \(x = 0\) のとき、\(y\) は定義されるか？

16. \(x\) が有理数のとき \(0\)、\(x\) が無理数のとき \(1\) となる関数が次の式で表せることを示せ: \[ y = \lim_{m \to \infty} \text{sgn}\{\sin^{2}(m!\, \pi x)\} \] ここで 例 31.14 と同様 \[ \text{sgn } x = \lim_{n \to \infty} (2/\pi)\arctan(nx) \] とする。 [\(x\) が有理数なら、\(\sin^{2}(m!\, \pi x)\) および \(\text{sgn}\{\sin^{2}(m!\, \pi x)\}\) はある \(m\) から後ろで全て \(0\) となる。\(x\) が無理数なら \(\sin^{2}(m!\, \pi x)\) は常に正で、\(\text{sgn}\{\sin^{2}(m!\, \pi x)\}\) は常に \(1\) となる]

    この \(y\) が次の形でも表せると示せ: \[ 1 - \lim_{m \to\infty} [\lim_{n \to\infty}\{\cos(m!\, \pi x)\}^{2n}] \]

17. 級数 \[ \sum_{1}^{\infty} \frac{1}{\nu(\nu + 1)},\quad \sum_{1}^{\infty} \frac{1}{\nu(\nu + 1)\cdots(\nu + k)} \] の和を求めよ。

    [次が成り立つ: \[ \frac{1}{\nu(\nu + 1)\cdots(\nu + k)} = \frac{1}{k} \biggl\{\frac{1}{\nu(\nu + 1)\cdots(\nu + k - 1)} - \frac{1}{(\nu + 1)(\nu + 2)\cdots(\nu + k)}\biggr\} \] よって \[ \sum_{1}^{n} \frac{1}{\nu(\nu + 1)\cdots(\nu + k)} = \frac{1}{k}\left\{\frac{1}{1·2\cdots k} - \frac{1}{(n + 1)(n + 2)\cdots (n + k)}\right\} \] であり、したがって \[ \sum_{1}^{\infty} \frac{1}{\nu(\nu + 1)\cdots (\nu + k)} = \frac{1}{k(k!)} \] が成り立つ]

18. \(|z| \lt |\alpha|\) なら \[ \frac{L}{z - \alpha} = -\frac{L}{\alpha}\left(1 + \frac{z}{\alpha} + \frac{z^{2}}{\alpha^{2}} + \cdots\right) \] であり、\(|z|\gt|\alpha|\) なら \[ \frac{L}{z - \alpha} = \frac{L}{z}\left(1 + \frac{\alpha}{z} + \frac{\alpha^{2}}{z^{2}} + \cdots\right) \] が成り立つ。

19. \(z\) のべきを使った \(\dfrac{Az + B}{az^{2} + 2bz + c}\) の展開: \(az^{2} + 2bz + c = 0\) の根を \(\alpha,\ \beta\) とすれば \(az^{2} + 2bz + c = a(z - \alpha)(z - \beta)\) となる。\(A,\ B,\ a,\ b,\ c\) が全て実数で \(\alpha \neq \beta\) とすれば \[ \frac{Az + B}{az^{2} + 2bz + c} = \frac{1}{a(\alpha - \beta)} \left(\frac{A\alpha + B}{z - \alpha} - \frac{A\beta + B}{z - \beta}\right) \] が容易に分かる。このとき \(b^{2} \gt ac\) と \(b^{2} \lt ac\) に応じて二つの場合がある。

    1. \(b^{2} \gt ac\) なら \(\alpha\) と \(\beta\) は異なる実数である。\(|z|\) が \(|\alpha|\) と \(|\beta|\) より小さいなら \(1/(z - \alpha)\) と \(1/(z - \beta)\) は \(z\) の昇べきの級数に展開でき、\(|z|\) が \(|\alpha|\) と \(|\beta|\) より小さいなら降べきの級数に、\(|z|\) が \(|\alpha|\) と \(|\beta|\) の間にあるなら一つが降べきの級数、もう一つが小べきの級数に展開される。結果を自分で書いてみるとよい。\(|z|\) が \(|\alpha|\) または \(|\beta|\) に等しいならこういった展開はできない。

    2. \(b^{2} \lt ac\) なら根は共役な複素数である (§43)。よって \(\rho^{2} = \alpha\beta = c/a,\ \rho\cos\phi = \frac{1}{2}(\alpha + \beta) = - b/a\) とすれば \[ \alpha = \rho\operatorname{Cis}\phi, \quad \beta = \rho\operatorname{Cis}(-\phi) \] であり、\(\cos\phi = -\sqrt{b^{2}/ac},\ \sin\phi = \sqrt{1 - (b^{2}/ac)}\) が成り立つ。

       \(|z| \lt \rho\) なら二つの関数は \(z\) の昇べきの級数で表せる。\(z^{n}\) の係数は \[ \frac{A\rho\sin n\phi + B\sin\{(n + 1)\phi\}}{a\rho^{n+1} \sin\phi} \] となる。\(|z| \gt \rho\) のときは同様の降べきの級数が得られる。\(|z| = \rho\) のときは展開できない。

20. \(|z| \lt 1\) なら \[ 1 + 2z + 3z^{2} + \cdots + (n + 1)z^{n} + \cdots = \frac{1}{(1 - z)^{2}} \] だと示せ。

    [第 \(n\) 項までの和は \(\dfrac{1 - z^{n}}{(1 - z)^{2}} - \dfrac{nz^{n}}{1 - z}\) となる]

21. \(L/(z - \alpha)^{2}\) を \(z\) の級数に展開せよ。\(|z| \lt |\alpha|\) のときは昇べきの級数、\(|z| \gt |\alpha|\) のときは降べきの級数となる。

22. \(b^{2} = ac\) かつ \(|az| \lt |b|\) なら \[ \frac{Az + B}{az^{2} + 2bz + c} = \sum_{0}^{\infty} p_{n}z^{n} \] が成り立つ。ここで \(p_{n} = \{(-a)^{n}/b^{n+2}\} \{(n + 1)aB - nbA\}\) である。\(|az| \gt |b|\) のときに対応する \(z\) の降べきの級数を求めよ。

23. 問題 19 の結果を \(\dfrac{1}{1 + z^{2}}\) に対して確かめよ。

    [\(\dfrac{1}{1 + z^{2}} = \sum z^{n} \sin\{\frac{1}{2}(n + 1)\pi\} = 1 - z^{2} + z^{4} - \cdots\) となる]

24. \(|z| \lt 1\) なら \[ \frac{1}{1 + z + z^{2}} = \frac{2}{\sqrt{3}} \sum_{0}^{\infty} z^{n} \sin\{\tfrac{2}{3}(n + 1)\pi\} \] だと示せ。

25. \(\dfrac{1 + z}{1 + z^{2}},\ \dfrac{1 + z^{2}}{1 + z^{3}},\ \dfrac{1 + z + z^{2}}{1 + z^{4}}\) を昇べきの \(z\) の級数に展開せよ。その展開が成り立つのは \(z\) がどんな値のときか？

26. \(\dfrac{a}{a + bz + cz^{2}} = 1 + p_{1}z + p_{2}z^{2} + \cdots\) なら \[ 1 + p_{1}^{2}z + p_{2}^{2}z^{2} + \cdots = \frac{a + cz}{a - cz}\cdot \frac{a^{2}}{a^{2} - (b^{2} - 2ac)z + c^{2}z^{2}} \] が成り立つ。

    (Math. Trip. 1900.)

27. \(\lim\limits_{n \to \infty} s_{n} = l\) なら \[ \lim_{n \to \infty} \frac{s_{1} + s_{2} + \cdots + s_{n}}{n} = l \] が成り立つ。

    [\(s_{n} = l + t_{n}\) として、\(t_{n}\) が \(0\) に向かうとき \((t_{1} + t_{2} + \cdots + t_{n})/n\) も \(0\) に向かうと示す。

    \(t_{1},\ t_{2},\ \ldots,\ t_{n}\) を \(t_{1},\ t_{2},\ \ldots,\ t_{p}\) と \(t_{p+1},\ t_{p+2},\ \ldots,\ t_{n}\) に分割する。ここで \(p\) は \(n\) の関数であり、\(n \to \infty\) のとき \(\infty\) に向かう。ただし \(p\) が無限大に向かう速度は \(n\) より遅い、つまり \(p \to \infty\) のとき \(p/n \to 0\) とする。例えば \(p\) は「\(\sqrt{n}\) の整数部分」という関数だとする。

    \(\varepsilon\) を任意の正の実数とする。\(\varepsilon\) がどれだけ小さくとも、\(n \geq n_{0}\) で \(t_{p+1},\ t_{p+2},\ \ldots,\ t_{n}\) の絶対値が全て \(\frac{1}{2}\varepsilon\) より小さくなるように \(n_{0}\) を選べる。そして \[ \left| \frac{t_{p+1} + t_{p+2} + \cdots + t_{n}}{n} \right| \lt \frac{1}{2} \cdot \frac{\varepsilon(n - p)}{n} \lt \frac{1}{2} \varepsilon \] が成り立つ。\(t_{1},\ t_{2},\ \ldots, t_{p}\) の絶対値の最大値を \(A\) とすれば \[ \left| \frac{t_{1} + t_{2} + \cdots + t_{p}}{n} \right| \lt \frac{pA}{n} \] となる。\(n \to \infty\) のとき \(\frac{p}{n} \to 0\) だったから、\(n_{0}\) が十分大きければ全ての \(n \geq n_{0}\) でこれは \(\frac{1}{2}\varepsilon\) より小さくなる。よって \[ \left|\frac{t_{1} + t_{2} + \cdots + t_{n}}{n}\right| \leq \left|\frac{t_{1} + t_{2} + \cdots + t_{p}}{n}\right| + \left|\frac{t_{p+1} + \cdots + t_{n}}{n} \right| \lt \varepsilon \] が \(n \geq n_{0}\) で成り立つ。示したいことはこれで証明された。

    極限を上手く扱えるようになりたいなら、上の議論を詳しく見ておくべきである。この例のように式を二つに分け、それぞれの極限が \(0\) なことを異なる方法で示し、それによって元の式が \(0\) に収束することを示さなければならないケースは非常に多い。この方法の証明は一筋縄ではいかない。

    証明の要点は次の通りである: 添え字が大きいなら \(t_{n}\) は小さいという仮定の下で、\(n\) が大きいとき \((t_{1} + t_{2} + \cdots + t_{n})/n\) が小さいことを示せばよい。分子の級数を二つの部分に分ける。一つ目の部分に入る項は小さくないが、項の数が \(n\) と比べたとき少ない。二つ目の部分に入る項の数は少なくないが、項が小さいので和は \(n\) より小さい速度でしか増加しない。よって \((t_{1} + t_{2} + \cdots + t_{n})/n\) を分割した二つの級数の和は両方とも \(n\) が大きいとき \(n\) と比べて小さいと分かる]

28. \(n \to \infty\) で \(\phi(n) - \phi(n - 1)\to l\) なら \(\phi(n)/n \to l\) となる。

    [\(\phi(n) = s_{1} + s_{2} + \cdots + s_{n}\) とすれば \(\phi(n) - \phi(n - 1) = s_{n}\) となり、前問の結果に帰着される]

29. \(s_{n} = \frac{1}{2}\{1 - (-1)^{n}\}\) なら \(s_{n}\) が \(n\) の偶奇によって \(1\) または \(0\) となるが、\(n \to \infty\) のとき \((s_{1} + s_{2} + \cdots + s_{n})/n \to \frac{1}{2}\) が成り立つ。

    [ここから問題 27 の逆が偽だと分かる。この \(s_{n}\) は \(n \to \infty\) で振動する]

30. 次の級数の最初の \(n\) 項の和を \(c_{n},\ s_{n}\) とする: \[ \frac{1}{2} + \cos\theta + \cos 2\theta + \cdots,\quad \sin\theta + \sin 2\theta + \cdots\hphantom{\,} \] このとき \[ \lim \frac{c_{1} + c_{2} + \cdots + c_{n}}{n} = 0, \quad \lim \frac{s_{1} + s_{2} + \cdots + s_{n}}{n} = \frac{1}{2} \cot\frac{1}{2} \theta \] が成り立つ。

1. 最後のケースでは \(N\) が時間にも依存する。また囚人 \(x\) は確かな値を持つが、この値は時間によって変動する。そのため時間を考えに入れれば、この関係は二変数関数 \(y = F(x, t)\) の簡単な例となる。この関数が定義されるのは \(t\) のとある区間、具体的にはダートムーア刑務所が完成してから閉鎖されるまで、そして特定の正の整数 \(x\) についてだけとなる。\(x\) が取る値は \(t\) に応じて変わる。^[return]

2. ここでは \([x]\) を第二章の意味で使っている。^[return]

3. ブロムウィッチ著 Infinite Series, p.485 を参照。^[return]

4. この言い回しが持つ曖昧さに読者はすぐに気が付くだろう。「これこれの定理はほとんど明らかである」という言葉は二つの異なる意味を持つ。一つ目の意味は「この定理の正しさは疑いの余地がない」であり、例えば「\(2 + 2 = 4\)」や「二等辺三角形の底角は等しい」の正しさを示すときに使われる。定理がこの意味で「明らか」だったとしても、それが正しいと証明されているとは言えない。常識を使った直感的な推論は間違うことが多く、さらにたとえ定理が正しかったとしても、それが「明らか」だから証明しなくてよいということにはならない。数学の目標は前提を使った結論の導出であり、結論が前提と同じぐらい「明らか」であっても証明の必要性が損なわれることはないし、通常は証明がつまらなくなることもない。

   しかしときには、この例のように「これはほとんど明らかである」が全く異なる意味を持つ場合もある。このとき私たちは「少し考えればこの主張の正しさを理解できるのはもちろん、きちんとした証明の各行を想像することもできるだろう」を意味する。定理がこの意味で「明らか」な場合には、証明を省略することもある。これは証明が不必要なためでは決してなく、読者が自分で容易に思い付けるものを細かく書くのは時間と空間の無駄でしかないためである。^[return]

5. \(a_{0}\) も \(b_{0}\) も \(0\) でないという自然な仮定を置く。^[return]

6. 具体的には \(PQ/2^{n} \lt \varepsilon\) となればよい。^[return]

7. ここで使われている指数が正の整数のときの二項定理は初等代数の定理である。その他の場合の二項定理には無限級数の理論が必要であり、後で触れる。^[return]

8. 「発散する」と「振動する」という表現は著者によって異なる使われ方をするので、注意する必要がある。ここではブロムウィッチ著 Infinite Series と同じ定義を使った。ホブソン著 Theory of Functions of a Real Variable では級数が有限に振動するときに限って「振動する」という表現が使われ、無限に振動する級数は「発散する」とされる。多くの外国の著者は「発散する」を「収束しない」の意味で使う。^[return]

9. 訳注: ここで「小数 (decimal)」は \(0.a_{1}a_{2} \ldots \) という形で表された \(0\) から \(1\) の間にある実数を意味する。^[return]

10. 訳注: 循環しない桁を持たないことを言う。^[return]

11. この例の結果を適切に変更すれば、全て任意の大きさの小数に拡張できる。詳細な議論はブロムウィッチ著 Infinite Series, Appendix I を参照。^[return]

12. 実数の無限集合に必ずしも最小値が存在するとは限らない。例えば \[ 1,\ \frac{1}{2},\ \frac{1}{3},\ \ldots,\ \frac {1}{n},\ \ldots \] からなる集合には最小値がない。^[return]

13. 訳注: 原著では \(S\) の上限が "the upper bound of \(S\)" と呼ばれているが、これは標準的でないので変更した。下限についても同様。^[return]

14. 訳注: 原著では \(\phi(n)\) の上極限が "the upper limit of indetermination of \(\phi(n)\)" と呼ばれているが、これは標準的でないので変更した。下極限についても同様。^[return]

15. この結果の簡潔な証明が "Some Problems of Diophantine Approximation", Acto Mathematica, vol. xxxvii にいくつか載っている。^[return]

16. 訳注: 日本の文献では「コーシーの収束判定法」と呼ばれることが多い。^[return]

17. 第八章で示す証明の中にはこの条件を使うと単純化できるものがいくつかある。^[return]

18. \(\lim\{\psi(n) - \phi(n)\} = 0\) および両方の関数が極限 \(e\) に向かうことの証明はクリスタル著 Algebra, vol. ii, pp.78 にある。本書では第九章で違う方法を使って証明する^[return]

19. 問題 8–12 はブロムウィッチ著 Infinite Series から取った。^[return]