§110 導関数 (その 1)

曲線に自然に関連付けられる性質の議論に戻る。最も重要で明白な性質は、前章で見た、曲線の見た目がつながっているかどうかという性質である。この性質は連続関数の定義で表される。

直線・円・円錐曲線といった初等幾何学で登場する普通の曲線には他にもたくさんの一般的な性質がある。その中でおそらく最も単純で最も注目に値するのは、曲線の各点で有限の方向が定まる、言い換えると、曲線上の各点で接線が引けることである。読者も知っての通り、初等幾何学では曲線上の点 \(P\) における接線が「点 \(Q\) が点 \(P\) に向かって近づくときの、弦 \(PQ\) の"極限"」として定義される。この「極限」の存在するという仮定が意味することを考えよう。

図 36 の \(P\) は曲線上の固定された点で、\(Q\) は移動する点だとする。\(PM, QN \) は \(OY\) と平行で、\(PR\) は \(OX\) と平行である。\(P\) の座標を \((x,\ y)\) として \(Q\) の座標を \((x + h,\ y + k)\) とすれば、\(N\) が \(M\) の左にあるとき \(h\) は正となり、右にあるとき負となる。

\(P\) で曲線の接線が存在すると仮定していた。つまり弦 \(PQ\) の「極限」が存在する。\(P\) における接線 \(PT\) と \(OX\) の角度を \(\psi\) とする。このとき \(PT\) が \(PQ\) の「極限」であるとは、曲線の両側から \(Q\) を \(P\) に近づけたときの \(\angle QPR\) の極限が \(\psi\) であることを意味する。ここで一般的なケースと例外的なケースを区別する必要がある。

\(\phi\) が \(\frac{1}{2}\pi\) でない一般的なケースでは、\(PT\) と \(OY\) が平行でない。そして \(\angle RPQ\) は極限 \(\psi\) に向かう。つまり \[ \frac{RQ}{PR} = \tan \angle RPQ \] は極限 \(\tan \psi\) に向かう。ここで \[ \frac{RQ}{PR} = \frac{NQ - MP}{MN} = \frac{\phi(x + h) - \phi(x)}{h} \] だから、 \[ \lim_{h \to 0} \frac{\phi(x + h) - \phi(x)}{h} = \tan\psi \qquad \text{(1)} \] が成り立つ。

ここまでの式が符号の影響を受ける点に注意してほしい。つまり \(Q\) が \(P\) に左にあるなら \(RQ\) は負となる。しかし (1) が表す極限の収束は \(h\) の符号に影響されない。

つまり \(\phi(x)\) のグラフとして表される曲線が点 \(P\) で \(x\) 軸と垂直でない接線を持つとすれば、\(\phi(x)\) は「\(P\) の横座標を \(x\) とすると、\(h\) が \(0\) に向かうとき \(\{\phi(x + h) - \phi(x)\}/h\) が極限に向かう」という性質を持つ。

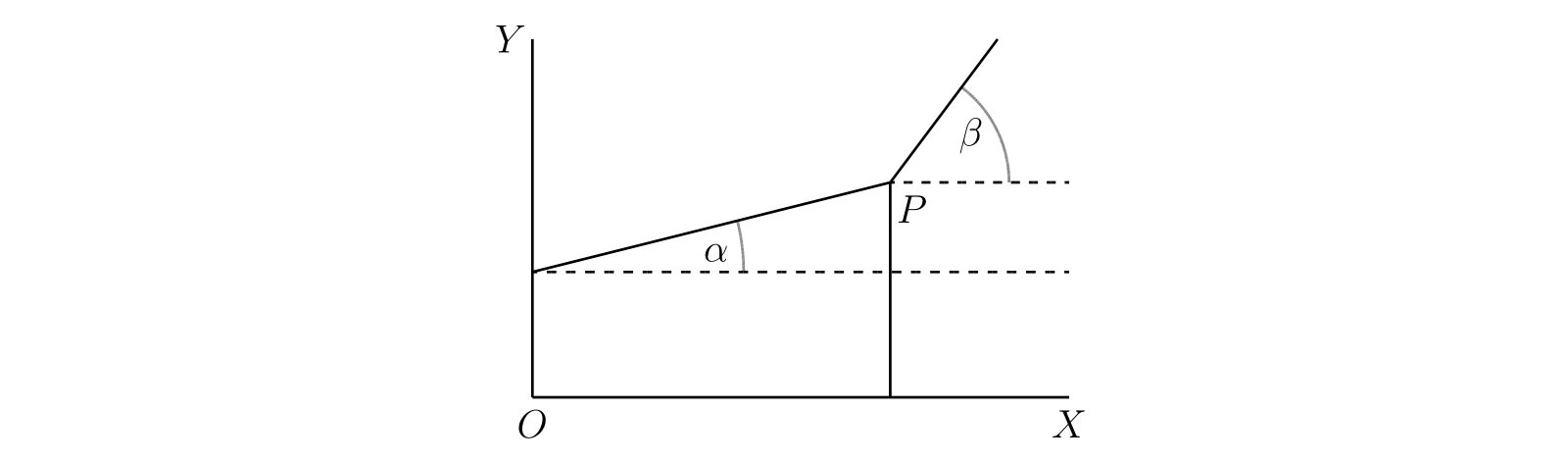
円や楕円のように曲線上の全ての点で接線が引ける、あるいは区間内の全ての \(x\) に対応するの点で接線が引けると仮定する。さらに接線が \(x\) 軸と垂直にならないとする。これにより例えば円を考えるときは半円よりも小さい弧を考えることになる。このとき式 \(\text{(1)}\) が区間内の全ての \(x\) で成り立つ。全ての \(x\) には対応する \(\tan \psi\) が存在するので、\(\tan \psi\) は \(x\) の関数となる。この関数は考えている全ての \(x\) に対して定義され、その値は元の関数 \(\psi(x)\) から計算・導出できる。この関数を導関数 (derivative, derived function) と呼び、次の記号で表す: \[ \phi'(x) \]

\(\phi(x)\) の導関数は \(\phi(x)\) の微分係数 (differential coefficient) とも呼ばれる。\(\phi(x)\) から \(\phi'(x)\) を求める操作を一般に微分 (differentiation) と呼ぶ。このような名前が付けられたのには歴史的な理由がある: §115 を見よ。

前述した例外では \(\psi = \frac{1}{2}\pi\) となる。この場合について詳しく考える前に、定義に関する注意や図を使った説明を行う。