§122 極大値と極小値 (その 1)

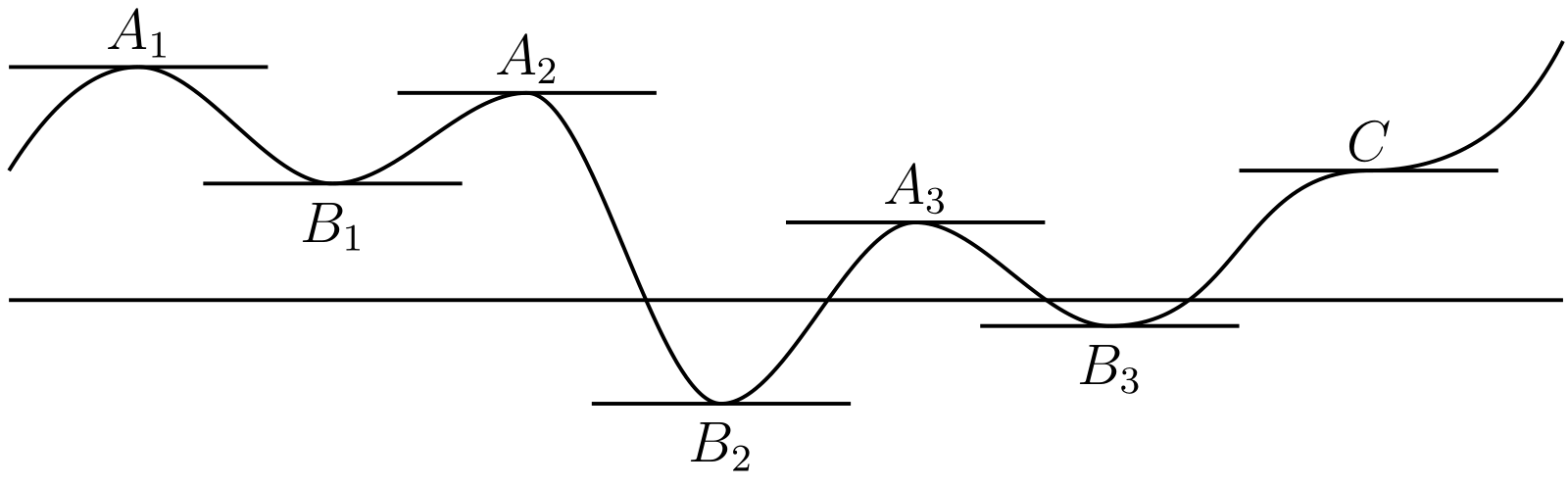
\(x = \xi\) における \(\phi(x)\) の値 \(\phi(\xi)\) が極大 (maximum) であるとは、\(x = \xi\) の近傍における任意の \(\phi(x)\) よりも \(\phi(\xi)\) の方が大きい、つまり \(\xi - \delta \lt x \lt \xi\) および \(\xi \lt x \lt \xi + \delta\) で \(\phi(\xi) \gt \phi(x)\) となる \(x\) の区間 \([\xi - \delta, \xi + \delta]\) が存在することを言う。同様に極小 (minimum) も定義する。例えば 図 39 ではグラフで表される関数が極大の点に \(A\) が対応し、極小の点に \(B\) が対応する。\(A_{3}\) が極大で \(B_{1}\) が極小の状況で \(B_{1}\) における関数の値が \(A_{3}\) における値よりも大きくなっているが、これは何も問題ないことに注意してほしい。

これは定理 A から直ちに従う。この条件が十分でないのは 図 39 の点 C を見ればすぐに分かる。あるいは \(y = x^{3}\) なら \(\phi'(x) = 3x^{2}\) であり \(x = 0\) で \(\phi'(x) = 0\) となるが、図 10 のグラフを見れば分かるように \(x^{3}\) は \(x = 0\) で極小でも極大でもない。

しかし「\(\phi'(\xi) = 0\)、かつ \(\xi\) より小さく十分 \(\xi\) に近い全ての \(x\) で \(\phi'(x) \gt 0\)、かつ \(\xi\) より大きく十分 \(\xi\) に近い全ての \(x\) で \(\phi'(x) \lt 0\) 」であれば \(\phi(x)\) は \(x = \xi\) で極大となることは言える。二つの不等式が反対向きなら \(x = \xi\) で極小となる。この仮定が成り立つとき §121 の系 3 より \(\phi(x)\) が \(x\) と共に増加するような区間 \([\xi - \delta, \xi]\) と \(\phi(x)\) が \(x\) と共に減少する区間 \([\xi, \xi + \delta]\) が存在し、これが \(\phi(\xi)\) が極大であることを保証する。

この結果は次のようにも表現できる: \(\phi'(x)\) の符号が \(x = \xi\) で正から負に変化するなら、\(\phi(x)\) は \(x = \xi\) で極大となる。\(\phi'(x)\) の符号が逆方向に変化するなら、\(\phi(x)\) は \(x = \xi\) で極小となる。

1. 連続であるが導関数を持たない関数にも極大および極小となる点が存在する場合がある。この定理ではもちろん導関数の存在を仮定している。^[return]