§124 極大値と極小値 (その 3)

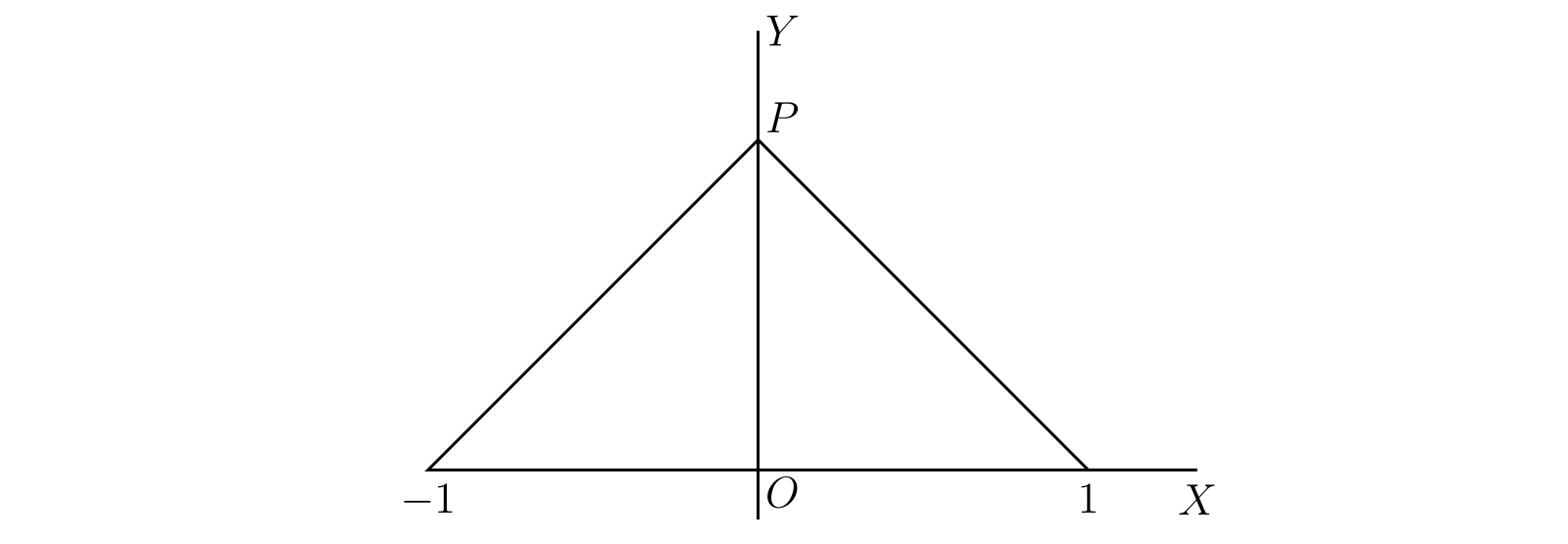
ここまでは (前節を除いて) 考えている区間に含まれる全ての $x$ で $ϕ (x)$ が導関数を持つ状況を考えてきた。この条件が満たされないなら定理は成り立たない。例えば次の関数は定理 B の前提を満たすが結論は満たさない: $y = 1 - x^{2}$ ただし平方根は正の値を取るとする。この関数のグラフを図 40 に示す。この関数は $ϕ (- 1) = ϕ (1) = 0$ を満たすが、図からも明らかなように $x$ が負なら $ϕ^{'} (x)$ は $- 1$ で $x$ が正なら $ϕ^{'} (x)$ は $1$ である。また $ϕ (x)$ は $x = 0$ で微分係数を持たず、グラフの点 $P$ では接線を引けない。つまり $ϕ (x)$ は明らかに $x = 0$ で極大となるにもかかわらず、 $ϕ^{'} (0)$ は存在せず、 $0$ と等しくない。つまり定理 B を使った極大性の判定が失敗する。

仮定したのは導関数 $ϕ^{'} (x)$ の存在だけだが、仮定されていない性質の中に特に重要なものが一つある: それは $ϕ^{'} (x)$ が連続関数かどうかである。ここから細かいことだが非常に興味深い疑問が生じる: 関数 $ϕ (x)$ が連続でない導関数を持つことはそもそもあり得るのか？言い換えると、各点で接線を引けるがその傾きが連続的に変化しないものが存在するか？常識に照らして考えれば、この疑問に「あり得ない」「存在しない」と答えたくなるかもしれない。しかしその答えが間違っていると示すのは難しくない。

関数 $ϕ (x)$ を $x \neq = 0$ のとき $ϕ (x) = x^{2} sin (1/ x)$ および $ϕ (0) = 0$ と定義する。このとき $ϕ (x)$ は全ての $x$ で連続となる。そして $x \neq = 0$ なら $ϕ^{'} (x) = 2 x sin (1/ x) - cos (1/ x)$ であり、そうでないなら $ϕ^{'} (0) = h \to 0 lim \frac{h ^{2} sin ( 1/ h )}{h} = 0$ が成り立つ。つまり $ϕ^{'} (x)$ は全ての $x$ に対して存在するが、 $ϕ^{'} (x)$ は $x = 0$ で不連続となる。 $x \to 0$ のとき $2 x sin (1/ x)$ は $0$ に向かうが、 $cos (1/ x)$ は下限 $- 1$ と上限 $1$ の間を振動する。よって $ϕ^{'} (x)$ も $- 1$ と $1$ の間を振動する。

本質的に同じ例を使うと §121 で予告した例が得られる。 $0 < a < 1$ に対して、 $x \neq = 0$ のとき $ϕ (x) = x^{2} sin (1/ x) + a x$ および $ϕ (0) = 0$ と定義する。すると $ϕ^{'} (0) = a > 0$ なので、定理 A の前提が満たされる。しかし $x \neq = 0$ のとき $ϕ^{'} (x) = 2 x sin (1/ x) - cos (1/ x) + a$ は下限 $a - 1$ と上限 $a + 1$ の間を振動する。 $a - 1 < 0$ だから、 $ϕ^{'} (x) < 0$ が成り立つ $x$ を $0$ に好きなだけ近くに見つけられる。よって $x = 0$ を含んだ区間であって $ϕ (x)$ が $x$ の単調増加関数となるものは存在しない。

ただし一般の導関数 $ϕ^{'} (x)$ が第五章の例 37.18 で説明した "単純な" 不連続性を持つことはない。つまり $x \to + 0$ のとき $ϕ^{'} (x) \to a$ で $x \to - 0$ のとき $ϕ^{'} (x) \to b$ で $ϕ^{'} (0) = c$ なら必ず $a = b = c$ であり、 $ϕ^{'} (x)$ は $x = 0$ で連続となる。証明は例 47.3 で行う。

例 46

定理 B が $ϕ (x) = (x - a)^{m} (x - b)^{n}$ と $ϕ (x) = (x - a)^{m} (x - b)^{n} (x - c)^{p}$ で正しいことを確認せよ。 $m, n, p$ は正の整数で $a < b < c$ とする。

[最初の関数は $x = a$ と $x = b$ で $0$ となる。そして $ϕ^{'} (x) = (x - a)^{m - 1} (x - b)^{n - 1} {(m + n) x - mb - na}$ は $x = (mb + na) / (m + n)$ で $0$ となるが、この値は $a$ と $b$ の間にある。二つ目の関数では二次方程式 $(m + n + p) x^{2} - {m (b + c) + n (c + a) + p (a + b)} x + mb c + n c a + p ab = 0$ が $a$ と $b$ および $b$ と $c$ の間に根を持つことを示す]
次の多項式が $x > 1$ で正だと示せ: $2 x^{3} + 3 x^{2} - 12 x + 7, 3 x^{4} + 8 x^{3} - 6 x^{2} - 24 x + 19$
任意の $x$ の区間で $x - sin x$ が増加関数であること、および $x$ が $- \frac{1}{2} π$ から $\frac{1}{2} π$ まで増加するとき $tan x - x$ が増加することを示せ。 $x$ の関数 $a x - sin x$ が単調増加および単調減少となるのは $a$ がどんな値のときか？
$tan x - x$ が $x = \frac{1}{2} π$ から $x = \frac{3}{2} π$ や $x = \frac{3}{2} π$ から $x = \frac{5}{2} π$ といった区間でも増加すること、および $tan x = x$ の根が各区間にちょうど一つずつ含まれることを示せ (参考: 例 17.4)。
問題 3 を使って $x > 0$ で $sin x - x < 0$ だと示し、ここから $cos x - 1 + \frac{1}{2} x^{2} > 0$ と $sin x - x + \frac{1}{6} x^{3} > 0$ を導け。一般に $x > 0$ に対して $C_{2 m} S_{2 m + 1} = cos x - 1 + \frac{x ^{2}}{2 !} - \dots - (- 1)^{m} \frac{x ^{2 m}}{( 2 m )!}, = sin x - x + \frac{x ^{3}}{3 !} - \dots - (- 1)^{m} \frac{x ^{2 m + 1}}{( 2 m + 1 )!}$ とすると、 $C_{2 m}$ と $S_{2 m + 1}$ は $m$ が奇数なら正で偶数なら負だと示せ。
$f (x)$ と $f^{''} (x)$ が連続かつ区間 $[a, b]$ で符号が一定なら、この区間には $f (x) = 0$ と $f^{'} (x) = 0$ の根がそれぞれ最大でも一つしか含まれないと示せ。
関数 $u, v$ の導関数 $u^{'}, v^{'}$ がとある区間で連続で、かつその区間で $u v^{'} - u^{'} v$ が $0$ にならないとする。適当な二つの $u = 0$ の根の間には $v = 0$ の根があること、およびその逆を示せ。 $u = cos x,$ $v = sin x$ としてこの事実を確かめよ。

[二つの $u = 0$ の根 $α$ と $β$ の間で $v$ が $0$ にならないとする。このとき関数 $u / v$ は区間 $[α, β]$ で連続であり、区間の端で $0$ となる。よって $(u / v)^{'} = (u^{'} v - u v^{'}) / v^{2}$ は $α$ と $β$ の間のどこかで $0$ になるが、これは仮定と矛盾する]
次の関数が極大および極小となる点を求めよ: $(x - 1)^{2} (x + 2), x^{3} - 3 x, 2 x^{3} - 3 x^{2} - 36 x + 10, 4 x^{3} - 18 x^{2} + 27 x - 7, 3 x^{4} - 4 x^{3} + 1, x^{5} - 15 x^{3} + 3$ それぞれの関数のグラフを描け。

[例として最後の関数を考える。この関数の導関数 $ϕ^{'} (x) = 5 x^{2} (x^{2} - 9)$ は $x = - 3, 0, 3$ で $0$ となる。少し調べれば $x = - 3$ が極大で $x = 3$ が極小だと分かるが、 $x = 0$ はどちらでもない。 $ϕ^{'} (x)$ は $x = 0$ の両方向で負となる]
関数 $(x - a)^{m} (x - b)^{n}$ の極大および極小について議論せよ。 $m$ と $n$ は正の整数として、 $m$ と $n$ が奇数および偶数のそれぞれの場合を考えること。さらにこの関数のグラフを描け。
前問と同じことを関数 $(x - a) (x - b)^{2} (x - c)^{3}$ について議論せよ。 $a, b, c$ の大小関係に応じてグラフの形がどう変わるか示せ。
$a, b, c, d$ がどんな値であっても、 $(a x + b) / (c x + d)$ が極大または極小となる点を持たないことを示せ。この関数のグラフを描け。
次の関数が極大および極小となる点について議論せよ: $y = \frac{a x ^{2} + 2 b x + c}{A x ^{2} + 2 B x + C}$ 分母は複素根を持つとする。

[ $a$ と $A$ は正だと仮定できる。導関数が $0$ になるのは $(a x + b) (B x + C) - (A x + B) (b x + c) = 0 (1)$ のときである。この方程式は実根を持つ: 持たないとすると導関数が常に同じ符号を持つことになるが、これは $y$ が全ての $x$ で連続で $x \to + \infty$ および $x \to - \infty$ のとき $y \to a / A$ という事実に反する。 $y$ のグラフは直線 $y = a / A$ とちょうど一回だけ交わるが、 $b / a > B / A$ なら十分大きい正の $x$ ではグラフがこの直線より上にあり、十分大きい負の $x$ ではグラフがこの直線より下にあること ( $b / a < B / A$ ならその逆) が示せる。よって $b / a > B / A$ なら $(1)$ の大きい方の根で $y$ は極大となり、小さい方の根で極小となる。 $b / a > B / A$ ならその逆が成り立つ]
前問の設定における $y$ の極大値と極小値は $a x^{2} + 2 b x + c - λ (A x^{2} + 2 B x + C)$ が $x$ の完全平方式となる $λ$ となる。 [これは $y = λ$ が曲線に接するための条件である]
一般に $R (x) = P (x) / Q (x)$ が極大または極小となる $x$ の値を $λ$ とすると、 $P (x) - λ Q (x) = 0$ は等しい根の組を持つ。
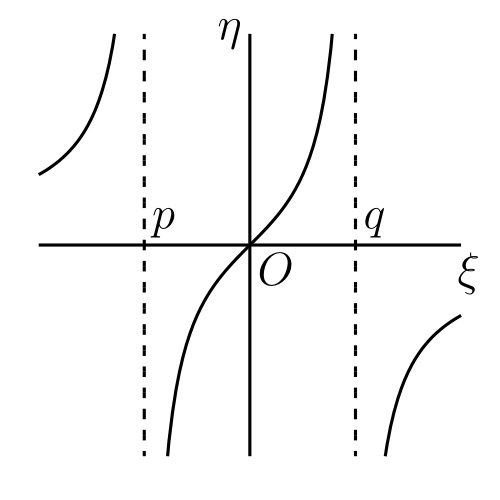
$A x^{2} + 2 B x + C = 0$ が実根を持つなら、議論は次のようになる。 $λ = b A - a B, μ = c A - a C$ とすると $y - \frac{a}{A} = \frac{λ x + μ}{A ( A x ^{2} + 2 B x + C )}$ が成り立つ。さらに $ξ = λ x + μ, η = (A / λ^{2}) (A y - a)$ とすれば $η = \frac{ξ}{( ξ - p ) ( ξ - q )}$ となる。

この $(x, y)$ から $(ξ, η)$ への変形は軸に平行な原点の移動・軸の縮小拡大・座標の反転 ( $λ < 0$ の場合) からなる。そのため $x$ の関数 $y$ の極小値は $ξ$ の関数 $η$ の極小値に対応する。この逆も成り立ち、極大値についても成り立つ。

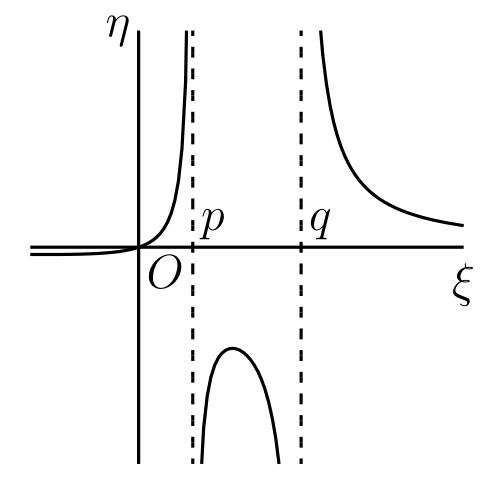
$ξ$ に関する $η$ の導関数は $(ξ - p) (ξ - q) - ξ (ξ - p) - ξ (ξ - q) = 0$ つまり $ξ^{2} = pq$ のとき $0$ となる。よって $η$ の導関数は $p$ と $q$ の符号が同じなら二つの根を持ち、異なるなら根を持たない。後者の場合の $η$ のグラフを図 41a に示す。

図 41a

図 41b

図 41c

$p$ と $q$ が正ならグラフは図 41b のようになり、 $ξ = pq$ で極大となり $ξ = - pq$ で極小となる¹。

$p = q$ なら $η = \frac{ξ}{( ξ - p ) ^{2}}$ であり、図 41c のようなグラフが得られる。

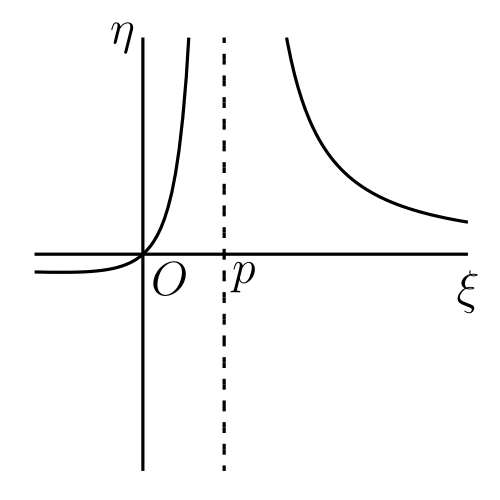
以上の議論は $λ \neq = 0$ を仮定している。 $λ = 0$ なら $a / A = b / B$ であり、 $y - \frac{a}{A} = \frac{μ}{A ( A x ^{2} + 2 B x + C )} = \frac{μ}{A ^{2} ( x - x _{1} ) ( x - x _{2} )}$ となる。 $d y / d x = 0$ とすると単一の値 $x = \frac{1}{2} (x_{1} + x_{2})$ を得る。グラフを描けば、 $μ$ が正ならこの値で極大となり、負なら極小となることが分かる。 $μ$ が正の場合のグラフを図 42 に示す。

[関数 $y = (a x^{2} + 2 b x + c) / (A x^{2} + 2 B x + C)$ に関する代数的な方法だけを使った完全な一般理論はクリスタル著 Algebra, vol i, pp. 464–7 にある]

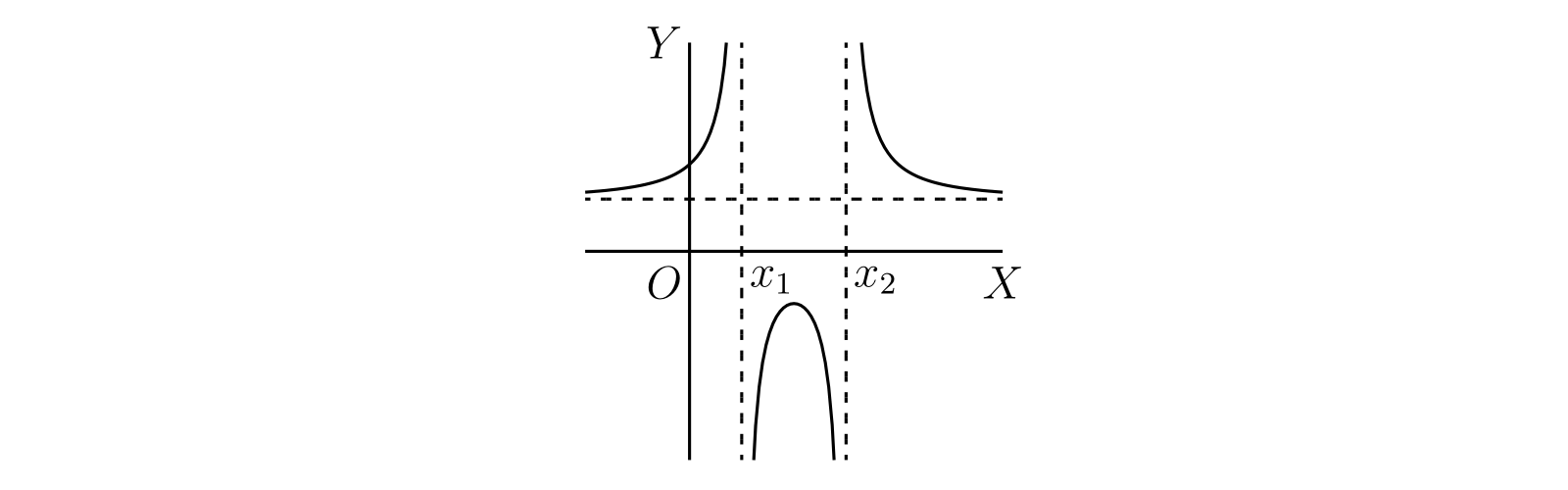図 42
$γ$ が $α$ と $β$ の間にあるなら、 $x$ が動くとき $(x - α) (x - β) / (x - γ)$ は全ての実数の値を取る。そうでないなら、長さ $4 ∣ α - γ ∣∣ β - γ ∣$ の区間を除いた全ての値を取る。
$0 < c < 1$ なら $y = \frac{x ^{2} + 2 x + c}{x ^{2} + 4 x + 3 c}$ が全ての実数の値を取ることを示し、この場合の関数のグラフを描け

(Math. Trip. 1910.)
$(a x^{2} + 2 b x + c) / (A x^{2} + 2 B x + C)$ の形をした関数であって $x = 1$ と $x = - 1$ でそれぞれ $2$ と $3$ の極大値または極小値を取り、 $x = 0$ では $2.5$ となるものを求めよ。

(Math. Trip. 1908.)
$a$ と $b$ が正なら、 $\frac{( x + a ) ( x + b )}{( x - a ) ( x - b )}$ の極大値と極小値は次の値である: $- (\frac{a + b}{a - b})^{2}, - (\frac{a - b}{a + b})^{2}$
$\frac{( x - 1 ) ^{2}}{( x + 1 ) ^{3}}$ の極大値は $\frac{2}{27}$ である。
次の関数の極大値と極小値について議論せよ: $\frac{x ( x - 1 )}{x ^{2} + 3 x + 3}, \frac{x ^{4}}{( x - 1 ) ( x - 3 ) ^{3}}, \frac{( x - 1 ) ^{2} ( 3 x ^{2} - 2 x - 37 )}{( x + 5 ) ^{2} ( 3 x ^{2} - 14 x - 1 )}$

(Math. Trip. 1898.)

[最後の関数を $P (x) / Q (x)$ と表記すれば $P^{'} Q - P Q^{'} = 72 (x - 7) (x - 3) (x - 1) (x + 1) (x + 2) (x + 5)$ が成り立つ]
$a cos x + b sin x$ が極大および極小となる $x$ の値を求めよ。関数を $A cos (x - B)$ の形に変形することでその結果の正しさを確かめよ。
次の関数が極大および極小となる $x$ の値を求めよ: $a^{2} cos^{2} x + b^{2} sin^{2} x, A cos^{2} x + 2 H cos x sin x + B sin^{2} x$
$\frac{sin ( x + a )}{sin ( x + b )}$ が極大値および極小値を持たないと示し、この関数のグラフを描け。
関数 $\frac{sin ^{2} x}{sin ( x + a ) sin ( x + b )} (0 < a < b < π)$ が極小値 $0$ と極大値 $- \frac{4 sin a sin b}{sin ^{2} ( a - b )}$ を無限に持つと示せ。

(Math. Trip. 1909.)
$a^{2} sec^{2} x + b^{2} cosec^{2} x$ の最小値は $(a + b)^{2}$ である。
$tan 3 x cot 2 x$ が $\frac{1}{9}$ と $\frac{3}{2}$ の間の値を取らないことを示せ。
直角三角形の斜辺ともう一つの辺の長さの和が固定されたとき、三角形の面積はその二つの辺の間の角度が $60°$ のとき最大になると示せ。

(Math. Trip. 1909)
固定点 $(a, b)$ を通る直線が $OX$ と $O Y$ に交わる点をそれぞれ $P$ と $Q$ とする。 $PQ, OP + OQ, OP \cdot OQ$ の最小値がそれぞれ $(a^{2/3} + b^{2/3})^{3/2}, (a + b)^{2}, 4 ab$ だと示せ。
楕円の接線が $x, y$ 軸と交わる点を $P, Q$ とする。 $PQ$ の最小値が短半径と長半径の積に等しいと示せ。
円錐曲線 $a x^{2} + 2 h x y + b y^{2} = 1$ の軸の長さと方向を求めよ。

[ $x$ 軸との角度が $θ$ で長さが $r$ の半径を持つ円錐曲線は $\frac{1}{r ^{2}} = a cos^{2} θ + 2 h cos θ sin θ + b sin^{2} θ$ で与えられる。 $r$ が極大および極小となる条件は $tan 2 θ = 2 h / (a - b)$ である。二つの方程式から $θ$ を消去すれば $(a - \frac{1}{r ^{2}}) (b - \frac{1}{r ^{2}}) = h^{2}$ を得る]
$x$ と $y$ が正で $x + y = k$ なら、 $x^{m} y^{n}$ の最大値は $\frac{m ^{m} n ^{n} k ^{m + n}}{( m + n ) ^{m + n}}$ である。
$x$ が $y$ が正で $x^{2} + x y + y^{2} = 3 κ^{2}$ を満たすとき、 $a x + b y$ の最大値は $2 κ a^{2} - ab + b^{2}$ である。

[ $a x + b y$ が極大なら $a + b (d y / d x) = 0$ が成り立つ。 $x$ と $y$ の関係からは $(2 x + y) + (x + 2 y) (d y / d x) = 0$ が分かる。二つの $d y / d x$ を等号で結べばよい]
$a, b, c$ を正の実数とする。 $θ$ と $ϕ$ が鋭角で $a sec θ + b sec ϕ = c$ が成り立つなら、 $a cos θ + b cos ϕ$ は $θ = ϕ$ のとき極小となる。

$- 1/ (p - q)^{2}$ が極大値で $- 1/ (p + q)^{2}$ が極小値となる。極小値の方が大きい。^[return]