第七章 微分と積分に関する諸定理
§147 高階の平均値の定理 (テイラーの定理)
§125 で証明したように、\(f(x)\) が区間 \([a, b]\) で導関数 \(f'(x)\) を持つとき、\(a \lt \xi \lt b\) を満たす \(\xi\) で \[ f(b) - f(a) = (b - a) f'(\xi) \] が成り立つ。同じことを言い換えると、\(f(x)\) が \([a, a + h]\) で導関数を持つなら、とある \(\theta_{1}\ \) (\(0 \lt \theta_{1} \lt 1\)) で \[ f(a + h) - f(a) = hf'(a + \theta_{1} h) \qquad \text{(1)} \] が成り立つ。この定理の証明では関数 \[ f(b) - f(x) - \frac{b - x}{b - a} \{f(b) - f(a)\} \] を考えた。この関数は \(x = a\) と \(x = b\) で \(0\) となる。
\(f(x)\) が \([a, b]\) で二次導関数 \(f''(x)\) を持つと仮定する。これにより一次導関数 \(f'(x)\) の連続性も仮定される。関数 \[ f(b) - f(x) - (b - x) f'(x) - \left(\frac{b - x}{b - a}\right)^{2} \{f(b) - f(a) - (b - a)f'(a)\} \] を考えると、この関数も \(x = a\) と \(x = b\) で \(0\) になる。この関数の導関数は \[ \frac{2(b - x)}{(b - a)^{2}} \{f(b) - f(a) - (b - a) f'(a) - \dfrac{1}{2}(b - a)^{2}f''(x)\} \] であり、これは \(a\) と \(b\) の間にある \(x\ \) (\(a\) と \(b\) は除く) で \(0\) になる (§121)。つまり \(a\) と \(b\) の間のとある \(\xi\) で次の等式が成り立つ: \[ f(b) = f(a) + (b - a)f'(a) + \dfrac{1}{2}(b - a)^{2}f''(\xi) \] \(\theta_{2}\ \) (\(0 \lt \theta_{2} \lt 1\)) を使えば \(\xi = a + \theta_{2}(b - a)\) という形で表すこともできる。
\(b = a + h\) とすれば \[ f(a + h) = f(a) + hf'(a) + \dfrac{1}{2}h^{2} f''(a + \theta_{2}h) \qquad \text{(2)} \] を得る。これは二次の平均値の定理 (Mean Value Theorem of the second order) と呼ばれる命題の標準形である。
\(\text{(1)}\) と \(\text{(2)}\) を一般化すると、次の定理が導かれる:
\(x\) の関数 \(f(x)\) が \([a, b]\) で \(n\) 次までの導関数を持つなら、ある \(\theta_{n}\ \) (\(0 \lt \theta_{n} \lt 1\)) で \[ \begin{aligned} f(a + h) & = f(a) + hf'(a) + \dfrac{1}{2} h^{2}f''(a) + \cdots \\ & \qquad \quad \cdots + \frac{h^{n-1}}{(n - 1)!} f^{(n-1)}(a) + \frac{h^{n}}{n!} f^{(n)}(a + \theta_{n}h) \end{aligned} \] が成り立つ。
証明は \(n = 1\) と \(n = 2\) の特殊な場合と同じように進む。関数 \[ F_{n}(x) - \left(\frac{b - x}{b - a}\right)^{n} F_{n}(a) \] を考える。ここで \[ F_{n}(x) = f(b) - f(x) - (b - x)f'(x) - \frac{(b - x)^{2}}{2!} f''(x) - \cdots - \frac{(b - x)^{n-1}}{(n - 1)!} f^{(n-1)}(x) \] である。この関数は \(x = a\) と \(x = b\) で \(0\) になる。よってその導関数 \[ \frac{n(b - x)^{n-1}}{(b - a)^{n}} \left\{F_{n}(a) - \frac{(b - a)^{n}}{n!} f^{(n)}(x)\right\} \] は \(a\) と \(b\) の間のとある \(x\) で \(0\) になる。示すべき結果はここから得られる。
この定理は非常に重要なので、章の終わりで別証明を示す。ここで示した証明と本質的に異なるわけではないが、式の形が違っており、部分積分が利用される。
-
\(f(x)\) を \(r\) 次の多項式とする。このとき \(f^{(n)}(x)\) は \(n \gt r\) で \(0\) に等しく、テイラーの定理は代数的な恒等式 \[ f(a + h) = f(a) + hf'(a) + \frac{h^{2}}{2!} f''(a) + \cdots + \frac{h^{r}}{r!} f^{(r)}(a) \] となる。
-
定理を \(f(x) = \dfrac{1}{x}\) に適用すると、正の \(x\) と \(x + h\) に対して次の結果が得られる: \[ \frac{1}{x + h} = \frac{1}{x} - \frac{h}{x^{2}} + \frac{h^{2}}{x^{3}} - \cdots + \frac{(-1)^{n-1} h^{n-1}}{x^{n}} + \frac{(-1)^{n} h^{n}}{(x + \theta_{n} h)^{n+1}} \]
[等式 \[ \frac{1}{x + h} = \frac{1}{x} - \frac{h}{x^{2}} + \frac{h^{2}}{x^{3}} - \cdots + \frac{(-1)^{n-1} h^{n-1}}{x^{n}} + \frac{(-1)^{n} h^{n}}{x^{n}(x + h)}\quad \] が成り立つから、\(x^{n}(x + h)\) を \((x + \theta_{n}h)^{n+1}\) の形に表せることから示したい結果を確認できる。また \(x^{n+1} \lt x^{n}(x + h) \lt (x + h)^{n+1}\) という明らかな不等式を使っても示せる]
-
等式 \[ \begin{aligned} \sin(x + h) = & \sin x + h\cos x - \frac{h^{2}}{2!}\sin x - \frac{h^{3}}{3!}\cos x + \cdots\\ \cdots & + (-1)^{n-1}\frac{h^{2n-1}}{(2n - 1)!}\cos x + (-1)^{n} \frac{h^{2n}}{2n!}\sin(x + \theta_{2n} h) \end{aligned} \] および \(\cos(x + h)\) に関する同様の等式、そして \(h^{2n+1}\) まで展開する等式を示せ。
-
\(m\) を正の整数、\(n\) を \(m\) 以下の正の整数としたとき \[ (x + h)^{m} = x^{m} + \binom{m}{1}x^{m-1} h + \cdots + \binom{m}{n - 1}x^{m-n+1} h^{n-1} + \binom{m}{n}(x + \theta_{n} h)^{m-n} h^{n} \] を示せ。さらに \([x, x + h]\) が \(x = 0\) を含まないならこの等式が全ての実数1 \(m\) と全ての正の整数 \(n\) に対して成り立つこと、そして \(x \lt 0 \lt x + h\) あるいは \(x + h \lt 0 \lt x\) であっても \(m - n\) が正ならこの等式が成り立つことを示せ。
-
\(f(x) = 1/x\) かつ \(x \lt 0 \lt x + h\) なら、\(f(x + h) = f(x) + hf'(x + \theta_{1}h)\) という関係は成り立たない。 [\(f(x + h) - f(x) \gt 0\) と \(hf'(x + \theta_{1} h) = -h/(x + \theta_{1} h)^{2} \lt 0\) から分かる。平均値の定理の前提条件が満たされない]
-
\(x = -a,\ h = 2a,\ f(x) = x^{1/3}\) とすると、等式 \[ f(x + h) = f(x) + hf'(x + \theta_{1} h) \] は \(\theta_{1} = \frac{1}{2} ± \frac{1}{18}\sqrt{3}\) で満たされる。 [この例は、定理の証明に用いた前提条件が満たされなくても結果が成り立つ場合があることを示している]
-
ニュートン法による方程式の根の近似: 代数方程式 \(f(x) = 0\) の根の近似値を \(\xi\) として、実際の根を \(\xi + h\) とする。このとき \[ 0 = f(\xi + h) = f(\xi) + hf'(\xi) + \dfrac{1}{2} h^{2}f''(\xi + \theta_{2}h) \] であり、ここから \[ h = -\frac{f(\xi)}{f'(\xi)} - \dfrac{1}{2} h^{2} \frac{f''(\xi + \theta_{2}h)}{f'(\xi)} \] が分かる。
つまり \[ x = \xi - \frac{f(\xi)}{f'(\xi)} \] は一般に \(x = \xi\) より優れた近似となる。もし根が単純な根なら \(f'(\xi + h) \neq 0\) であり、\(h\) を十分小さくとれば考えている全ての \(x\) で \(|f'(x)| \gt K\) となるように定数 \(K\) を選べる。このとき \(h\) が一次の小ささを持つとすれば \(f(\xi)\) は一次の小ささであり、誤差 \(\xi - \{f(\xi)/f'(\xi)\}\) は二次の小ささを持つ。
-
最初の近似値を \(\xi = 3/2\) として \(x^{2} = 2\) に対してこの手続きを実行せよ。 [\(h = -1/12,\ \) \(\xi + h = 17/12 = 1.417\ldots\) となり、一度の実行にもかかわらずかなり正確な値が得られる。\(\xi = 17/12\) として手続きを反復すれば \(\xi + h = 577/408 = 1.414215\ldots\) が得られる。これは小数第五位まで正しい]
-
\(y\) が小さいときの \(x^{2} - 1 - y = 0\) を前問および前々問と同様に考えることで、近似的に \(\sqrt{1 + y} = 1 + \frac{1}{2} y - \{\frac{1}{4}y^{2}/(2 + y)\}\) であり、この近似の誤差は四次だと示せ。
-
\(f(x) = 0\) の根を \(\xi - (f/f') - \frac{1}{2}(f^{2}f''/{f'}^{3})\) と近似したときの誤差が三次だと示せ。全ての関数の引数は \(\xi\) とする。
-
\(\alpha\) が小さいとき、方程式 \(\sin x = \alpha x\) は \(\pi\) にほぼ等しい根を持つ。\((1 - \alpha)\pi\) が \(\pi\) よりも優れた近似であり、\((1 - \alpha + \alpha^{2})\pi\) はさらに優れた近似であることを示せ。
-
一般的な平均値の定理に出てくる \(\theta_{n}\) の \(h \to 0\) における極限が \(\dfrac{1}{n + 1}\) だと示せ。\(f^{(n+1)}(x)\) は連続とする。
[\(f(x + h)\) は次の二つの式と等しい: \[ \begin{gathered} f(x) + \cdots + \frac{h^{n}}{n!} f^{(n)}(x + \theta_{n}h),\\ f(x) + \cdots + \frac{h^{n}}{n!} f^{(n)}(x) + \frac{h^{n+1}}{(n + 1)!} f^{(n+1)}(x + \theta_{n+1}h) \end{gathered} \] ここで \(\theta_{n+1}\) と \(\theta_{n}\) は両方とも \(0\) と \(1\) の間にある。ここから \[ f^{(n)}(x + \theta_{n}h) = f^{(n)}(x) + \frac{hf^{(n+1)}(x + \theta_{n+1}h)}{n + 1} \] を得る。また一次の平均値の定理で \(h\) を \(\theta_{n}h\) としたものを \(f^{(n)}(x)\) に適用すれば \[ f^{(n)}(x + \theta_{n}h) = f^{(n)}(x) + \theta_{n}hf^{(n+1)}(x + \theta\theta_{n}h) \] であり、この \(\theta\) も \(0\) と \(1\) の間にある。よって \[ \theta_{n} f^{(n+1)}(x + \theta\theta_{n} h) = \frac{f^{(n+1)}(x + \theta_{n+1} h)}{n + 1} \] が成り立つ。\(f^{(n+1)}(x + \theta\theta_{n} h)\) と \(f^{(n+1)}(x + \theta_{n+1} h)\) はどちらも \(h \to 0\) で極限 \(f^{(n+1)}(x)\) に向かうから、示すべき式が得られる]
-
\(h \to 0\) のとき \(\{f(x + 2h) - 2f(x + h) + f(x)\}/h^{2} \to f''(x)\) だと示せ。\(f''(x)\) は連続とする。 [§147 の式 \(\text{(2)}\) を使う]
-
\(x = 0\) で \(f^{(n)}(x)\) が連続なら \[ f(x) = a_{0} + a_{1}x + a_{2}x^{2} + \cdots + (a_{n} + \varepsilon_{x}) x^{n} \] であり、\(a_{r} = f^{(r)}(0)/r!\) および \(x \to 0\) のとき \(\varepsilon_{x} \to 0\) だと示せ2。
-
等式 \[ a_{0} + a_{1}x + a_{2}x^{2} + \cdots + (a_{n} + \varepsilon_{x}) x^{n} = b_{0} + b_{1}x + b_{2}x^{2} + \cdots + (b_{n} + \eta_{x}) x^{n} \] が成り立っていて、さらに \(\varepsilon_{x}\) と \(\eta_{x}\) が \(x \to 0\) のとき \(0\) に向かうとする。このとき \(a_{0} = b_{0},\ a_{1} = b_{1},\ \ldots,\ a_{n} = b_{n}\) だと示せ。 [\(x \to 0\) とすれば \(a_{0} = b_{0}\) が分かる。次に \(x\) で割ってから \(x \to 0\) とすれば \(a_{1} = b_{1}\) が分かる。後はこの手続きを好きなだけ繰り返せばよい。この命題と前問の結果を使えば、 \(f(x) = a_{0} + a_{1}x + a_{2}x^{2} + \cdots + (a_{n} + \varepsilon_{x}) x^{n}\) で \(f(x)\) の最初の \(n\) 個の導関数が連続なら \(a_{r} = f^{(r)}(0)/r!\) だと分かる]
§148 テイラー級数
点 \(x = a\) を囲む区間 \([a - \eta, a + \eta]\) で \(f(x)\) の全ての導関数が連続とする。\(h\) の絶対値が \(\eta\) より小さいなら、全ての \(n\) に対して \(\theta_{n}\ \) (\(0 \lt \theta_{n} \lt 1\)) があって \[ f(a + h) = f(a) + hf'(a) + \cdots + \frac{h^{n-1}}{(n - 1)!} f^{(n-1)}(a) + \frac{h^{n}}{n!} f^{(n)}(a + \theta_{n} h), \] が成り立つ。つまり \[ S_{n} = \sum_{0}^{n-1} \frac{h^{\nu}}{\nu!} f^{(\nu)}(a),\quad R_{n} = \frac{h^{n}}{n!} f^{(n)}(a + \theta_{n} h) \] とすれば、 \[ f(a + h) - S_{n} = R_{n} \] が成り立つ。
加えて \(n \to \infty\) で \(R_{n} \to 0\) とすれば、 \[ f(a + h) = \lim_{n\to\infty} S_{n} = f(a) + hf'(a) + \frac{h^{2}}{2!} f''(a) + \cdots \] となる。
この \(f(a + h)\) の展開にはテイラー級数 (Teylor's Series) という名前が付いている。\(a = 0\) とした \[ f(h) = f(0) + hf'(0) + \frac{h^{2}}{2!} f''(0) + \cdots \] はマクローリン級数 (Maclaurin's Series) と呼ばれ、関数 \(R_{n}\) はラグランジュの剰余項 (Lagrange's form of the remainder) と呼ばれる。
\(f(x)\) の全ての導関数の連続ならテイラー級数が存在するなどと思ってはいけない。どんなときでも \(R_{n}\) の振る舞いの直接的な議論が欠かせない。
-
\(f(x) = \sin x\) とする。\(f(x)\) の全ての導関数は全ての \(x\) で連続となる。加えて全ての \(x\) と \(n\) で \(|f^{n}(x)| \leq 1\) が成り立つ。よって \(|R_{n}| \leq h^{n}/n!\) であり、\(h^{n}/n!\) は \(h\) の値に関わらず \(n \to \infty\) のとき \(0\) に向かう (例 27.12)。ここから \[ \sin(x + h) = \sin x + h\cos x - \frac{h^{2}}{2!}\sin x - \frac{h^{3}}{3!}\cos x + \frac{h^{4}}{4!}\sin x + \cdots \] が全ての \(x\) と \(h\) で成り立つと分かる。特に全ての \(h\) に対して \[ \sin h = h - \frac{h^{3}}{3!} + \frac{h^{5}}{5!} - \cdots \] である。同様に \[ \begin{aligned} \cos(x + h) & = \cos x - h\sin x - \frac{h^{2}}{2!}\cos x + \frac{h^{3}}{3!} \sin x + \cdots,\quad \\ \cos h & = 1 - \frac{h^{2}}{2!} + \frac{h^{4}}{4!} - \cdots \end{aligned} \] を示せる。
-
二項級数: \(m\) を正または負の有理数として、\(f(x) = (1 + x)^{m}\) と定める。このとき \(f^{(n)}(x) = m(m - 1) \cdots (m - n + 1) (1 + x)^{m-n}\) だから、マクローリン級数は次の形となる: \[ (1 + x)^{m} = 1 + \binom{m}{1}x + \binom{m}{2}x^{2} + \cdots \]
\(m\) が正の整数なら級数は途中で打ち切られ、正の整数に対する通常の二項定理が得られる。一般的な場合には \[ R_{n} = \frac{x^{n}}{n!} f^{(n)}(\theta_{n}x) = \binom{m}{n}x^{n}(1 + \theta_{n}x)^{m-n} \] だから、ある \(x\) の区間で正の整数でない \(m\) に対してこのマクローリン級数が本当に \((a + x)^{m}\) を表すと示すには、その区間の全ての \(x\) で \(R_{n} \to 0\) を示さなければならない。実は \(R_{n}\) は \(-1 \lt x \lt 1\) で収束し、\(0 \leq x \lt 1\) の場合の収束は簡単に示せる。\(0 \leq x \lt 1\) なら \(n \gt m\) のとき \((1 + \theta_{n}x)^{m-n} \lt 1\) であり、\(n \to \infty\) のとき \(\dbinom{m}{n} x^{n} \to 0\) が成り立つ (例 27.13)。しかし \(-1 \lt x \lt 0\) のときには証明が難しくなる。\(n \gt m\) では \(1 + \theta_{n}x \lt 1\) と \((1 + \theta_{n}x)^{m-n} \gt 1\) が成り立つが、\(0 \lt \theta_{n} \lt 1\) だけでは「\(1 + \theta_{n}x\) がとても小さく \((1 + \theta _{n}x)^{m-n}\) がとても大きい」というケースを排除できない。
実はテイラーの定理を使って二項定理を証明するには、\(R_{n}\) を別の形で表す必要がある。これは §162 で示す。
§149 テイラーの定理を使った極大値と極小値の計算
テイラーの定理を使うと §122–§123 で示した極値の判定法が理論的に完全なものになる (ただしこの結果が実際に役に立つわけではない)。\(\phi(x)\) が一次と二次の導関数を持つなら、\(\phi(x)\) が \(x = \xi\) で極大となるための十分条件は \(\phi'(\xi) = 0\) かつ \(\phi''(\xi) \lt 0\) であり、極小となるための十分条件は \(\phi'(\xi) = 0\) かつ \(\phi''(\xi) \gt 0\) だった。\(\phi''(\xi)\) と \(\phi'(\xi)\) がどちらも \(0\) だとこの方法では判定できなくなる。
最初の \(n\) 個の導関数 \[ \phi'(x),\quad \phi''(x),\quad \ldots,\quad \phi^{(n)}(x) \] が連続で、\(x = \xi\) で \(\phi^{(n)}(x)\) 以外が全て \(0\) になるとする。このとき十分小さい \(h\) で \[ \phi(\xi + h) - \phi(\xi) = \frac{h^{n}}{n!} \phi^{(n)} (\xi + \theta_{n} h) \] が成り立つ。極大値または極小値が存在するには、十分小さい全ての \(h\) でこの式の符号が一定でなければならない。ここから \(n\) は偶数だと分かる。\(n\) が偶数で \(\phi^{(n)}(\xi)\) が負なら極大値が、正なら極小値が存在する。
こうして判定法が得られる:
極大値または極小値が存在するには、\(0\) でない値を持つ一番次数の低い導関数が偶数次なことが十分である。その値が負なら極大値が存在し、正なら極小値が存在する。
-
この結果を \(\phi(x) = (x - a)^{m}\) に対して確かめよ。\(m\) は正の整数で、\(\xi = a\) とする。
-
\(m\) と \(n\) を正の整数として、関数 \((x - a)^{m} (x - b)^{n}\) が \(x = a\) と \(x = b\) で極大または極小となるか判定せよ。曲線 \(y = (x - a)^{m} (x - b)^{n}\) のグラフを可能な形それぞれについて描け。
-
次の関数が \(x = 0\) で極大または極小となるか判定せよ: \[ \begin{aligned} & \sin x - x,\quad\sin x - x + \frac{x^{3}}{6},\quad\sin x - x + \frac{x^{3}}{6} - \frac{x^{5}}{120}, &&\ldots,\\ & \cos x - 1,\quad\cos x - 1 + \frac{x^{2}}{2},\quad\cos x - 1 + \frac{x^{2}}{2} - \frac{x^{4}}{24}, &&\ldots \end{aligned} \]
§150 テイラーの定理を使った極限の計算
\(x\) の関数 \(f(x)\) と \(\phi(x)\) の導関数 \(f'(x)\) と \(\phi'(x)\) が \(x = \xi\) で連続であり、\(f(\xi)\) と \(\phi(\xi)\) が両方とも \(0\) だとする。このとき関数 \[ \psi(x) = \frac{f(x)}{\phi(x)} \] は \(x = \xi\) で定義されない。しかしもちろん \(\psi(x)\) が \(x \to \xi\) で極限に向かう可能性はある。
さて \(\xi\) と \(x\) の間の \(x_{1}\) に対して \[ f(x) = f(x) - f(\xi) = (x - \xi)f'(x_{1}) \] であり、同様に \(\xi\) と \(x\) の間の \(x_{2}\) に対して \(\phi(x) = (x - \xi)\phi'(x_{2})\) が成り立つ。したがって \[ \psi(x) = \frac{f'(x_{1})}{\phi'(x_{2})} \] が分かる。このとき四つの異なる場合が存在する。
-
\(f'(\xi) \neq 0\) かつ \(\phi'(\xi) \neq 0\) なら \[ \frac{f(x)}{\phi(x)} \to \frac{f'(\xi)}{\phi'(\xi)} \] が成り立つ。
-
\(f'(\xi) = 0\) かつ \(\phi'(\xi) \neq 0\) なら \[ \dfrac{f(x)}{\phi(x)} \to 0 \] が成り立つ。
-
\(f'(\xi) \neq 0\) かつ \(\phi'(\xi)= 0\) なら、\(\dfrac{f(x)}{\phi(x)}\) の絶対値は \(x \to \xi\) のとき非常に大きくなる。ただし \(\dfrac{f(x)}{\phi(x)}\) が \(\infty\) に向かうのか、\(-\infty\) に向かうのか、それともあるときは正に大きくてあるときは負に大きくなるのかを判定するには、\(x \to \xi\) のとき \(\phi'(x)\) がどのように \(0\) に向かうかについての情報が必要になる。
-
\(f'(\xi) = 0\) かつ \(\phi'(\xi) = 0\) なら、\(x \to 0\) における \(\dfrac{f(x)}{\phi(x)}\) の振る舞いに関して言えることは何もない。
最後の二つのケースでは、\(f(x)\) と \(\phi(x)\) が連続な二次導関数を持つ場合がある。もしそうなら \[ \begin{aligned} f(x) & = f(x) - f(\xi) - (x - \xi)f'(\xi) = \dfrac{1}{2}(x - \xi)^{2} f''(x_{1}),\\ \phi(x) & = \phi(x) - \phi(\xi) - (x - \xi)\phi'(\xi) = \dfrac{1}{2}(x - \xi)^{2} \phi''(x_{2}) \end{aligned} \] であり、\(x_{1}\) と \(x_{2}\) は \(\xi\) と \(x\) の間にある。ここから \[ \psi(x)= \frac{f''(x_{1})}{\phi''(x_{2})} \] が分かる。この式についても上と同じような場合分けが生じる。特に \(x = \xi\) で二次導関数がどちらも \(0\) にならないなら \[ \frac{f(x)}{\phi(x)} \to \frac{f''(\xi)}{\phi''(\xi)} \] が成り立つ。
明らかに以上の議論はいくらでも繰り返すことができ、次の結果が得られる:
\(f(x)\) と \(\phi(x)\) および (考えるだけの) その導関数が全て \(x = \xi\) で連続とする。\(f^{(p)}(x)\) と \(\phi^{(q)}(x)\) を \(x = \xi\) で \(0\) にならない \(f(x)\) と \(\phi(x)\) の導関数であって一番次数の低いものとすれば、次が成り立つ:
- \(p = q\) なら \(\dfrac{f(x)}{\phi(x)} \to \dfrac{f^{(p)}(\xi)}{\phi^{(p)}(\xi)}\) となる。
- \(p \gt q\) なら \(\dfrac{f(x)}{\phi(x)} \to 0\) となる。
- \(p \lt q\) で \(q - p\) が偶数なら \(\dfrac{f(x)}{\phi(x)} \to +\infty\) または \(\phi(x) \to -\infty\) であり、符号は \(\dfrac{f^{(p)}(\xi)}{\phi^{(q)}(\xi)}\) と同じになる。
- \(p \lt q\) で \(q - p\) が奇数なら \(x \to \xi + 0\) のとき \(\dfrac{f(x)}{\phi(x)} \to +\infty\) または \(\dfrac{f(x)}{\phi(x)} \to -\infty\) であり、符号は \(\dfrac{f^{(p)}(\xi)}{\phi^{(q)}(\xi)}\) と同じになる。\(x \to \xi - 0\) では符号が反転する。
この結果は次の式からすぐに得られる系である: \[ f(x) = \frac{(x - \xi)^{p}}{p!}f^{(p)}(x_{1}),\quad \phi(x) = \frac{(x - \xi)^{q}}{q!}\phi^{(q)}(x_{2}) \]
-
\(x \to 1\) における次の関数の極限を求めよ: \[ \frac{x - (n + 1)x^{n+1} + nx^{n+2}}{(1 - x)^{2}} \] [この関数とその一次導関数は \(x = 1\) で \(0\) となり、\(f''(1) = n(n + 1)\) と \(\phi''(1) = 2\) が成り立つ]
-
\(x \to 0\) における次の式の極限を求めよ: \[ \dfrac{\tan x - x}{x - \sin x},\quad \dfrac{\tan nx - n\tan x}{n\sin x - \sin nx} \]
-
\(x \to \infty\) における \(x\{\sqrt{x^{2} + a^{2}} - x\}\) の極限を求めよ。 [\(x = 1/y\) とする]
-
次を示せ: \[ \begin{gathered} \lim_{x \to n} (x - n)\cosec x\pi = \frac{(-1)^{n}}{\pi},\\ \lim_{x \to n} \frac{1}{x - n} \left\{ \cosec x\pi - \frac{(-1)^{n}}{(x - n)\pi} \right\} = \frac{(-1)^{n}\pi}{6} \end{gathered} \]
\(n\) は整数とする。\(\cot x\pi\) を使った同様の極限も求めよ。
-
\(x \to 0\) における次の式の極限を求めよ: \[ \frac{1}{x^{3}}\left(\cosec x - \frac{1}{x} - \frac{x}{6}\right),\quad \frac{1}{x^{3}}\left(\cot x - \frac{1}{x} + \frac{x}{3}\right) \]
-
\(x \to 0\) のとき \(\dfrac{\sin x\arcsin x - x^{2}}{x^{6}} \to \dfrac{1}{18}\) および \(\dfrac{\tan x\arctan x - x^{2}}{x^{6}} \to \dfrac{2}{9}\) が成り立つ。
§151 平面曲線の交点
ある点が二つの曲線の両方に存在するとき、二つの曲線はその点で交わる (intersect) と言う。さらにその点における接線が同じなら、二つの曲線はその点で接する (touch) と言う。
二つの関数 \(f(x)\) と \(\phi(x)\) について、全ての次数の導関数が \(x = \xi\) で連続とする。曲線 \(y = f(x)\) と \(y = \phi(x)\) を考える。一般に \(f(\xi)\) と \(\phi(\xi)\) は異なっており、\(x = \xi\) という横座標は交点に対応しない。しかしもし \(f(\xi) = \phi(\xi)\) なら、\(x = \xi,\ y = f(\xi) = \phi(\xi)\) という点で曲線が交わる。二つの曲線がこの点で交わるとする。さらに曲線がこの点で接するには、一次導関数 \(f'(x)\) と \(\phi'(x)\) が \(x = \xi\) で等しいことが必要十分である。
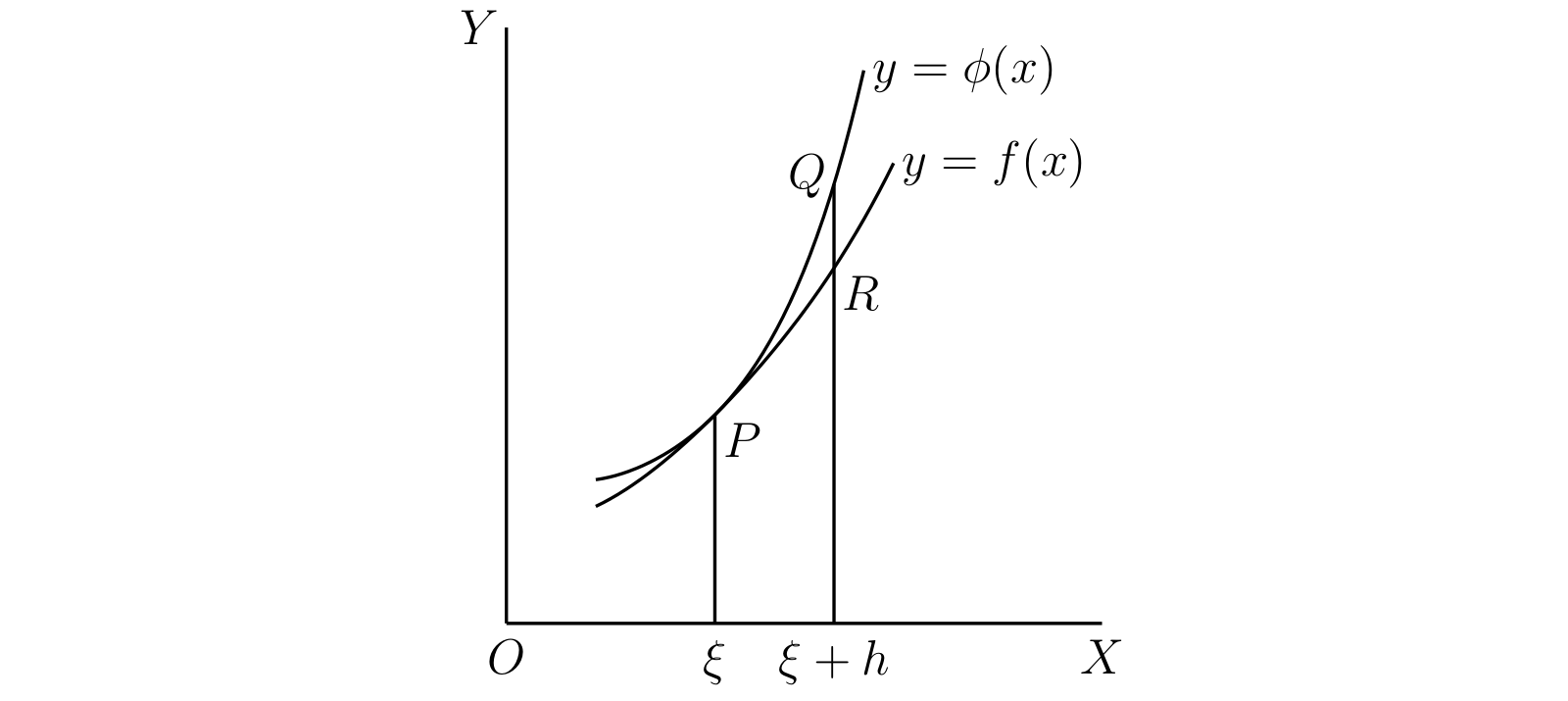
曲線が接触する点は異なる視点からも観察できる。上図では二つの曲線が \(P\) で接しており、\(QR\) が \(\phi(\xi + h) - f(\xi + h)\) に等しい。\(\phi(\xi) = f(\xi)\) および \(\phi'(\xi) = f'(\xi)\) だから、\(QR\) は \[ \dfrac{1}{2} h^{2}\{\phi''(\xi + \theta h) - f''(\xi + \theta h)\} \] にも等しい。ここで \(\theta\) は \(0\) から \(1\) の間の実数を表す。ここから \(h \to 0\) で \[ \lim \frac{QR}{h^{2}} = \dfrac{1}{2}\{\phi''(\xi) - f''(\xi)\} \] だと分かる。言い換えると、\(x\) 座標が \(\xi\) の点で二つの曲線が接するなら、\(\bm{x}\) 座標が \(\bm{\xi + h}\) の点における曲線の \(\bm{y}\) 座標の差は \(\bm{h}\) が小さいとき二次の小ささを持つ。
簡単に分かるように、曲線が交わるが接しはしないとき \(\lim (QR/h) = \phi'(\xi) - f'(\xi)\) が成り立ち、\(QR\) は一次の小ささを持つ。
つまり \(QR\) の小ささの次数を曲線の接触点の近さの指標として採用できる。つまり \(f\) と \(\phi\) の \(n - 1\) 次までの導関数が \(x = \xi\) で同じ値を取るなら、\(QR\) は \(n\) 次の小ささを持つ。この事実および次の式を示すのは難しくない: \[ \lim \frac{QR}{h^{n}} = \frac{1}{n!}\{\phi^{(n)}(\xi) - f^{(n)}(\xi)\} \] よって次の定義が得られる:
\(f(\xi) = \phi(\xi),\ f'(\xi) = \phi'(\xi),\ \ldots,f^{(n)}(\xi) = \phi^{(n)}(\xi)\) および \(f^{(n+1)}(\xi) \neq \phi^{(n+1)}(\xi)\) なら、曲線 \(y = f(x)\) と \(y = \phi(x)\) の \(x\) 座標が \(\xi\) の点を \(n\) 次の接触点 (contact of the \(n\)th order) と呼ぶ。
\(n\) 次の接触点に関するここまでの議論は軸の取り方に依存しており、接線が \(y\) 軸と平行なときには行えない。\(y\) が独立変数で \(x\) が従属変数だとみなせばこの場合を扱えるが、\(x\) と \(y\) の両方をパラメータ \(t\) の関数とみなした方が分かりやすい。この理論の素晴らしい解説が §147 で示したフォウラー氏による文献およびド・ラ・ヴァレ・プーサン著 Cours d'Analyse, vol. ii, pp. 396 et seq. にある。
-
\(\phi(x) = ax + b\) なら \(y = \phi(x)\) は直線となる。\(x = \xi\) の点が接点となる条件は \(f(\xi) = a\xi + b\) かつ \(f'(\xi) = a\) である。この条件が満たされる \(a\) と \(b\) を計算すれば \(a = f'(\xi)\) と \(b = f(\xi) - \xi f'(\xi)\) を得る。よって \(x = \xi\) における \(y = f(x)\) の接線の方程式は \[ y = xf'(\xi) + \{f(\xi) - \xi f'(\xi)\} \] つまり \(y - f(\xi) = (x - \xi)f'(\xi)\) となる (参考: 例 39.5)。
-
曲線上の点で接する直線は一意に決定される。接線と曲線が二次の接触点を持つには、\(f''(\xi) = \phi''(\xi)\) つまり \(f''(\xi) = 0\) でなければならない。曲線の接線が二次の接触点を持つ点を変曲点 (point of inflexion) と呼ぶ。
-
次の関数の変曲点を求めよ: \[ 3x^{4} - 6x^{3} + 1,\quad \dfrac{2x}{1 + x^{2}},\quad \sin x,\quad a\cos^{2}x + b\sin^{2}x,\quad \tan x,\quad \arctan x \]
-
円錐曲線 \(ax^{2} + 2hxy + by^{2} + 2gx + 2fy + c = 0\) が変曲点を持たないことを示せ。 [添え字で微分を表せば \(ax + hy + g + (hx + by + f)y_{1} = 0\) および \[ a + 2hy_{1} + by_{1}^{2} + (hx + by + f)y_{2} = 0 \] が成り立つ。よって変曲点において \[ a + 2hy_{1} + by_{1}^{2} = 0 \] が分かる。ここから \[ a(hx + by + f)^{2} - 2h(ax + hy + g)(hx + by + f) + b(ax + hy + g)^{2} = 0 \] つまり \[ (ab - h^{2})\{ax^{2} + 2hxy + by^{2} + 2gx + 2fy\} + af^{2} - 2fgh + bg^{2} = 0 \] となる。しかしこれが成り立つのは、円錐曲線の方程式が \[ af^{2} - 2fgh + bg^{2} = c(ab - h^{2}) \] つまり \(abc + 2fgh - af^{2} - bg^{2} - ch^{2} = 0\) を満たすときに限られる。これは円錐曲線が二つの直線に退化するための条件である]
-
\(y = \dfrac{ax^{2} + 2bx + c}{\alpha x^{2} + 2\beta x + \gamma}\) は \(\alpha x^{2} + 2\beta x + \gamma = 0\) が実根を持つなら一つの変曲点を、虚根を持つなら三つの変曲点を持つ。
[原点を変更することで、この方程式で表される曲線は次の形に変形できる (参考: 例 46.15): \[ \eta = \frac{\xi}{A\xi^{2} + 2B\xi + C} = \frac{\xi}{A(\xi - p)(\xi - q)} \] \(p\) と \(q\) は実数または複素数を表す。変曲点の条件は \(\xi^{3} - 3pq\xi + pq(p + q) = 0\) となる。これは \(\{pq(p - q)\}^{2}\) の正負に応じて一つまたは三つの実根を持つ。つまり \(p\) と \(q\) が実数か複素数かに応じて変曲点の数が変化する]
-
具体的な曲線 \(y = \dfrac{1 - x}{1 + x^{2}},\ y = \dfrac{1 - x^{2}}{1 + x^{2}},\ y = \dfrac{1 + x^{2}}{1 - x^{2}}\) の変曲点について議論せよ。
-
問題 5 の曲線が三つの変曲点を持つとき、それらが一直線上にあることを示せ。 [方程式 \(\xi^{3} - 3pq\xi + pq(p + q) = 0\) は \((\xi - p)(\xi - q)(\xi + p + q) + (p - q)^{2}\xi = 0\) と変形できる。すなわち、変曲点は直線 \(\xi + A(p - q)^{2}\eta + p + q = 0\) つまり \(A\xi - 4(AC - B^{2})\eta = 2B\) 上にある]
-
曲線 \(y = x\sin x\) と \(y = \dfrac{\sin x}{x}\) が無限に多くの変曲点を持つと示せ。
-
曲線の接触点と曲率3: 一般的な円の方程式 \[ (x - a)^{2} + (y - b)^{2} = r^{2} \qquad \text{(1)} \] には任意定数が三つ含まれる。この定数を、円と曲線 \(y = f(x)\) の接触点 \((\xi, \eta)\) がなるべく高い次数になるように定める問題を考える。ここで \(\eta = f(\xi)\) として、\(f'(\xi)\) と \(f''(\xi)\) を \(\eta_{1}\) および \(\eta_{2}\) と書く。円の方程式を二回微分すると \[ (x - a) + (y - b)y_{1} = 0, \qquad \text{(2)} \] \[ 1 + y_{1}^{2} + (y - b)y_{2} = 0 \qquad \text{(3)} \] が分かる。
もし円が曲線と接するなら、\(\text{(1)}\) と \(\text{(2)}\) が \(x = \xi,\ y = \eta,\ y_{1} = \eta_{1}\) で満たされる。ここから \((\xi - a)/\eta_{1} = -(\eta - b) = r/\sqrt{1 + \eta_{1}^{2}}\) が分かる。もし接触点が二次なら加えて \(\text{(3)}\) も成り立つ。このとき \(b = \eta + \{(1 + \eta_{1}^{2})/\eta_{2}\}\) であり、まとめると \[ a = \xi - \frac{\eta_{1}(1 + \eta_{1}^{2})}{\eta_{2}},\quad b = \eta + \frac{1 + \eta_{1}^{2}}{\eta_{2}},\quad r = \frac{(1 + \eta_{1}^{2})^{3/2}}{\eta_{2}} \] となる。
曲線との二次の接触点 \((\xi, \eta)\) を持つ円を曲率円 (circle of curvature) と呼び、曲率円の半径を曲率半径 (radius of curvature)、曲率半径の逆数を曲率 (curvature) と呼ぶ。つまり曲率は \(f''(\xi)/\{1 + [f'(\xi)]^{2}\}^{3/2}\) すなわち \[ \frac{d^{2}\eta}{d\xi^{2}} \bigg/ \biggl\{1 + \biggl(\frac{d\eta}{d\xi}\biggr)^{2}\biggr\}^{3/2} \] に等しい。
-
円の曲率が一定であり、半径の逆数に等しいことを示せ。さらに曲率が一定の曲線は円に限ることを示せ。
-
円錐曲線 \(y^{2} = 4ax\) と \((x/a)^{2} + (y/b)^{2} = 1\) の曲率半径と曲率中心を求めよ。
-
楕円上の点 \(P\) における曲率半径は \(\dfrac{CD^{3}}{ab}\) である。\(CD\) は \(CP\) と共役な4半径の長さを表す。
-
曲線 \(y = f(x)\) 上の点 \(P\) が与えられたときに、\(y = f(x)\) と四次の接触点を持つ円錐曲線を描けることを一般的に示せ。
[一般的な円錐曲線の方程式 \[ ax^{2} + 2hxy + by^{2} + 2gx + 2fy + c = 0 \] を \(x\) に関して四回微分する。添え字で微分の回数を表す記法を使うと \[ \begin{aligned} ax + hy + g + (hx + by + f) y_{1} & = 0,\\ a + 2hy_{1} + by_{1}^{2} + (hx + by + f) y_{2} & = 0,\\ 3(h + by_{1}) y_{2} + (hx + by + f) y_{3} & = 0,\\ 4(h + by_{1}) y_{3} +3by_{2}^{2} + (hx + by + f) y_{4} & = 0 \end{aligned} \] を得る。円錐曲線が四次の接触点を持つなら、この五つの等式が \(x,\ y,\ y_{1},\ y_{2},\ y_{3},\ y_{4}\) の値が \(\xi,\ \eta,\ \eta_{1},\ \eta_{2},\ \eta_{3},\ \eta_{4}\) のとき成り立つ。つまり比 \(a : b : c : f : g : h\) を求めるのにちょうど必要な数の等式が得られる]
-
曲線上の点 \(P\) と三次の接触点を持つ円錐曲線は無限に描ける。それらの中心が同一直線上にあることを示せ。
[接線と法線を軸として取れば、円錐の方程式は \(2y = ax^{2} + 2hxy + by^{2}\) という形となる。\(x\) が小さいとき、\(y\) の値は第五章に関するその他の例 22より \[ y = \dfrac{1}{2}ax^{2} + \left(\dfrac{1}{2}ah + \varepsilon_{x}\right) x^{3} \] を満たす。ここで \(x \to 0\) のとき \(\varepsilon_{x} \to 0\) である。一方でこの式は \(x \to 0\) で \(\varepsilon'_{x} \to 0\) となる \(\varepsilon'_{x}\) を使った \[ y = \dfrac{1}{2}f''(0) x^{2} + \left(\dfrac{1}{6}f'''(0) + \varepsilon'_{x}\right) x^{3} \] と等しくなければならない。よって 例 55.15 から \(a = f''(0),\ h = \dfrac{f'''(0)}{3f''(0)}\) が分かる。そしてこの円錐曲線の中心は \(ax + hy = 0\) 上にある]
-
楕円 \((x/a)^{2} + (y/b)^{2} = 1\) の長軸の端と三次に接触する放物線を求めよ。
-
楕円 \((x/a)^{2} + (y/b)^{2} = 1\) 上の点 \((a\cos\alpha, b\sin\alpha)\) と三次に接触する円錐曲線の中心の軌跡は直径 \(x/(a\cos\alpha) = y/(b\sin\alpha)\) である。 [この楕円自身も条件を満たす円錐曲線であることから分かる]
§152 多変数関数の微分 (その 1)
ここまでは \(x\) という一つの変数の関数だけを考えてきた。しかし微分の考え方を \(x,\ y,\ \ldots\) という複数の変数の関数に拡張するのを妨げるものは何もない。
\(f(x, y)\) を二つの5実変数 \(x\) と \(y\) の関数として、極限 \[ \lim_{h\to 0}\frac{f(x + h, y) - f(x, y)}{h},\quad \lim_{k\to 0}\frac{f(x, y + k) - f(x, y)}{k} \] が考えている全ての \(x\) と \(y\) に対して存在すると仮定する。つまり \(f(x, y)\) が \(x\) に関する導関数 \(df/dx = D_{x}f(x, y)\) を持ち、さらに \(y\) に関する導関数 \(df/dy = D_{y}f(x, y)\) も持つとする。こういった導関数は \(f\) の偏微分係数 (partial differential coefficients) と呼ばれ、 \[ \frac{\partial f}{\partial x},\quad \frac{\partial f}{\partial y} \] あるいは \[ f_{x}'(x, y),\quad f_{y}'(x, y) \] と表記される。\(f_{x}',\ f_{y}'\) や \(f_{x},\ f_{y}\) と書かれることもある。ただしここで、こういった記法が本質的に新しい概念を定義していると考えてはいけない。\(x\) に関する "偏微分" は、手続きとして通常の微分と全く同一である。\(f\) が \(x\) とは独立な二つ目の引数 \(y\) を取る点にだけ気を付ければよい。
ここまでの議論は \(x\) と \(y\) が互いに独立だとして進めてきた。\(x\) と \(y\) が何らかの関係で結ばれているなら、話は大きく変わってくる。この場合 \(y\) を変えずに \(x\) を \(x + h\) に変えることができないので、上述の \(f_{x}'\) の定義が全く意味をなさなくなる。ただしこのとき \(f(x, y)\) は本当の意味で二変数関数ではない。第二章で定義した通り、二変数関数とは二つの独立変数を持つ関数である。\(y\) が \(x\) に依存しているなら、\(y\) は \(x\) の関数となる。この関数を \(y = \phi(x)\) と書けば \[ f(x, y) = f\{x, \phi(x)\} \] が単一の変数 \(x\) の関数に過ぎないことがはっきりする。もちろん \(f\) は単一の変数 \(y\) の関数としても表せる。あるいは \(x\) と \(y\) を第三の変数 \(t\) の関数とみなしたほうが分かりやすい場合も往々にしてある。このとき \(f(x, y)\) は \(f\{\phi(t), \psi(t)\}\) という形で表すことができ、単一の変数 \(t\) の関数となる。
-
\(x = r\cos\theta\) かつ \(y = r\sin\theta\) なら \(r = \sqrt{x^{2} + y^{2}}\) と \(\theta = \arctan(y/x)\) が成り立つ。このとき \[ \begin{aligned} \frac{\partial r}{\partial x} & = \frac{x}{\sqrt{x^{2} + y^{2}}}, & \frac{\partial r}{\partial y} & = \frac{y}{\sqrt{x^{2} + y^{2}}}, & \frac{\partial \theta}{\partial x} & = -\frac{y}{x^{2} + y^{2}}, & \frac{\partial \theta}{\partial y} & = \frac{x}{x^{2} + y^{2}},\\ \frac{\partial x}{\partial r} & = \cos\theta, & \frac{\partial y}{\partial r} & = \sin\theta, & \frac{\partial x}{\partial \theta} & = -r\sin\theta, & \frac{\partial y}{\partial \theta} & = r\cos\theta \end{aligned} \] を示せ。
-
\(\dfrac{\partial r}{\partial x}\neq 1\bigg/\biggl(\dfrac{\partial x}{\partial r}\biggr)\) と \(\dfrac{\partial \theta}{\partial x}\neq 1\bigg/\biggl(\dfrac{\partial x}{\partial \theta}\biggr)\) を説明せよ。
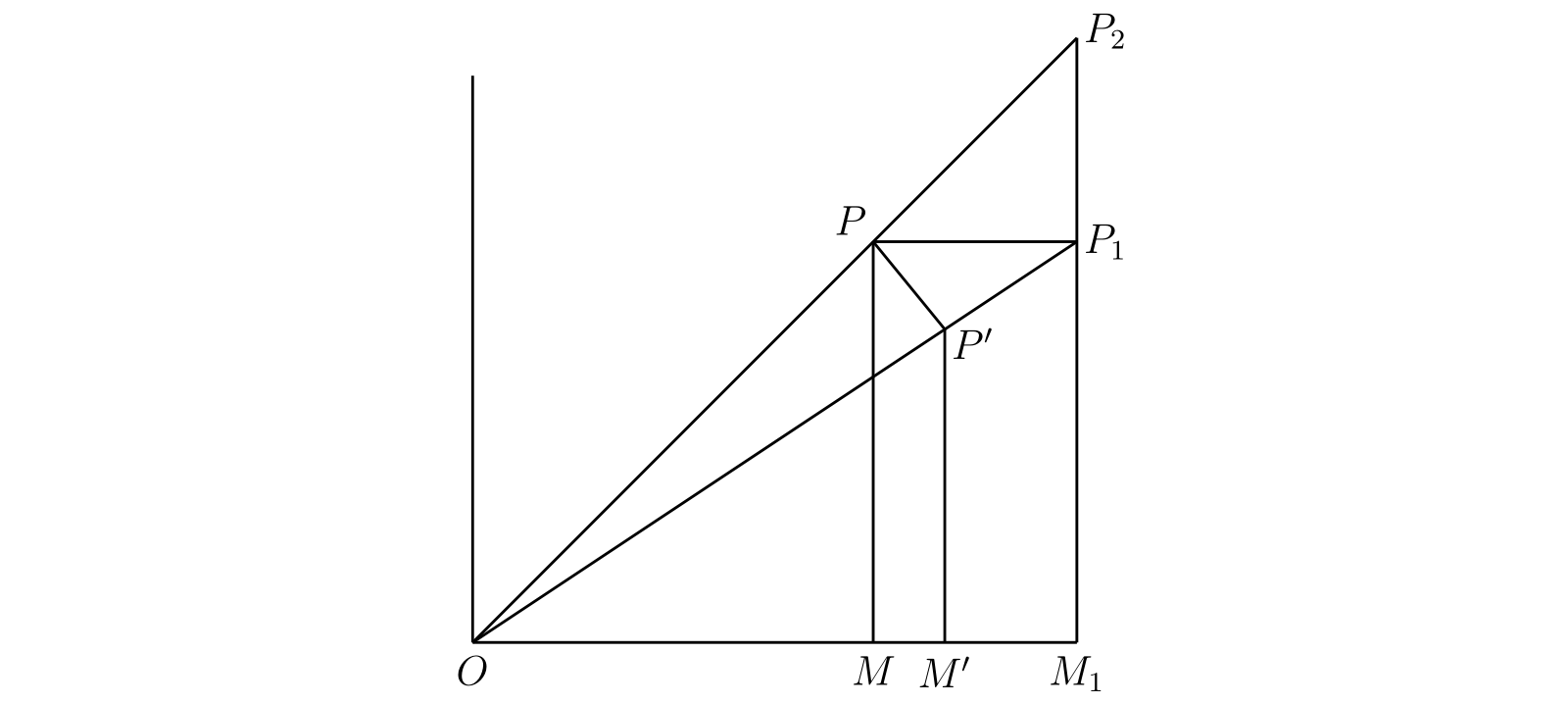 図 46
図 46[考えているのが単一の変数 \(x\) の関数 \(y\) のときは \(dy/dx\) と \(dx/dy\) の定義が互いの逆数であり、等号が成り立つ。しかし二変数関数ではこれは成り立たない。図 46 で \(P\) を点 \((x, y)\) あるいは \((r, \theta)\) とする。\(\partial r/\partial x\) を求めるには、\(y\) を定数に保ったまま \(x\) を増加させる必要がある。\(x\) の増分を \(MM_{1} = \delta x\) として、\(P\) の移動先を \(P_{1}\) とする。\(OP_{1}\) 上に \(OP' = OP\) となる \(P'\) を取ると、\(r\) の増分を \(P'P_{1} = \delta r\) と表せる。そして \(\partial r/\partial x = \lim(\delta r/\delta x)\) が成り立つ。一方で \(\partial x/\partial r\) を計算するには、\(x\) と \(y\) を \(r\) と \(\theta\) の関数とみなした上で \(\theta\) を一定に保ったまま \(r\) を \(\Delta r\) だけ増加させる必要がある。これによって \(P\) は \(P_{2}\) まで移動し、\(PP_{2} = \Delta r\) が成り立つ。対応する \(x\) の増分を \(MM_{1} = \Delta x\) とすれば \[ \frac{\partial x}{\partial r} = \lim \frac{\Delta x}{\Delta r} \] が成り立つ。すると \(\Delta x = \delta x\)6 かつ \(\Delta r \neq \delta r\) となる。実際 \[ \lim \frac{\delta r}{\delta x} = \lim \frac{P'P_{1}}{PP_{1}} = \cos\theta \] だが \[ \lim \frac{\Delta r}{\Delta x} = \lim \frac{PP_{2}}{PP_{1}} = \sec\theta \] であり、ここから \[ \lim \frac{\delta r}{\Delta r} = \cos^{2}\theta \] が分かる。
この関係の背後にあるのはもちろん\(\bm{\partial x/\partial r}\) と \(\bm{\partial r/\partial x}\) では \(\bm{P}\) の変動についての仮定が異なるという事実である]
-
\(z = f(ax + by)\) なら \(b\dfrac{\partial z}{\partial x} = a\dfrac{\partial z}{\partial y}\) だと示せ。
-
\(X + Y = x,\ Y = xy\) として \(\dfrac{\partial X}{\partial x},\ \dfrac{\partial X}{\partial y}\,\ \ldots\) を求めよ。\(x\) と \(y\) を \(X,\ Y\) の関数として表し、\(\dfrac{\partial x}{\partial X},\ \dfrac{\partial x}{\partial Y},\ \ldots\) を求めよ。
-
\(X + Y + Z = x,\ Y + Z = xy,\ Z = xyz\) として \(\dfrac{\partial X}{\partial x},\ \ldots\) を求めよ。\(X,\ Y,\ Z\) を使って \(x,\ y,\ z\) を表し、\(\dfrac{\partial x}{\partial X},\ \ldots\) を求めよ。
[この節の議論は任意の数の関数へと容易に拡張できる。ただし、複数の変数を持つ関数の偏微分は全ての独立変数が指定されてはじめて定義される点に注意が必要となる。例えば \(u = x + y + z\) で \(x,\ y,\ z\) が独立変数なら \(\partial u/\partial x = 1\) だが、\(u\) が \(x,\ x + y = \eta,\ x + y + z = \zeta\) という変数の関数だとすれば \(u = \zeta\) および \(\partial u/\partial x = 0\) となる]
§153 二変数関数の微分 (その 2)
一変数の関数の微分に関する全微分係数定理 (Theorem of the Total Differential Coefficient)と呼ばれる非常に重要な定理がある。この定理は前節で説明した二変数関数に関する概念を利用しており、 \[ f\{\phi(t), \psi(t)\} \] を \(t\) に関して微分する方法を与える。
最初に、\(x\) と \(y\) の二変数関数 \(f(x, y)\) が考えている全ての \(x,\ y\) で連続 (§107) な\(f_{x}',\ f_{y}'\) を持つ場合を考える。さらに \((x, y)\) の変動が曲線 \[ x = \phi(t),\quad y = \psi(t) \] に制限されていると仮定する。ここで \(\phi\) と \(\psi\) は \(t\) の関数で、連続な導関数 \(\phi'(t),\ \psi' (t)\) を持つ。このとき \(f(x, y)\) は単一の変数 \(t\) の関数となるので、これを \(F(t)\) と表記する。\(F'(t)\) を求める問題を考える。
\(t\) が \(t + \tau\) へ変化するとき \(x\) と \(y\) がそれぞれ \(x + \xi\) と \(y + \eta\) へ変化するなら、定義から \[ \begin{aligned} \frac{dF(t)}{dt} & = \lim_{\tau\to 0} \frac{1}{\tau}[f\{\phi(t + \tau), \psi(t + \tau)\} - f\{\phi(t), \psi(t)\}]\\ & = \lim \frac{1}{\tau}\{f(x + \xi, y + \eta) - f(x, y)\} \\ & = \lim \left[ \frac{f(x + \xi, y + \eta) - f(x, y + \eta)}{\xi}\, \frac{\xi}{\tau} + \frac{f(x, y + \eta) - f(x, y)}{\eta}\, \frac{\eta}{\tau} \right] \end{aligned} \] が分かる。
一方で平均値の定理からは、\(0\) と \(1\) の間にある実数 \(\theta\) と \(\theta'\) を使って \[ \begin{aligned} \frac{f(x + \xi, y + \eta) - f (x, y + \eta)}{\xi} & = f_{x}'(x + \theta\xi, y + \eta),\\ \frac{f(x, y + \eta) - f(x, y)}{\eta} \hphantom{{} + \xi} & = f_{y}'(x, y + \theta'\eta) \end{aligned} \] と書けることが分かる。\(\tau \to 0\) のとき \(\xi \to 0\) かつ \(\eta \to 0\) であり、さらに \(\xi/\tau \to \phi'(t)\) および \(\eta/\tau \to \psi'(t)\) そして \[ f_{x}'(x + \theta\xi, y + \eta) \to f_{x}'(x, y),\quad f_{y}'(x, y + \theta'\eta) \to f_{y}'(x, y) \] が成り立つ。よって \[ F'(t) = D_{t}f \{\phi(t), \psi(t)\} = f_{x}'(x, y)\phi'(t) + f_{y}'(x, y)\psi'(t) \] となる。この式を実際に計算するときには、まず \(x\) と \(y\) に関する微分を計算してから \(x = \phi(t)\) と \(y = \psi(t)\) を代入しなければならない。この結果の表記を変えれば \[ \frac{df}{dt} = \frac{\partial f}{\partial x}\, \frac{dx}{dt} + \frac{\partial f}{\partial y}\, \frac{dy}{dt} \] となる。
-
\(\phi(t) = \dfrac{1 - t^{2}}{1 + t^{2}},\ \psi(t) = \dfrac{2t}{1 + t^{2}}\) とすれば、\((x, y)\) の軌跡は円 \(x^{2} + y^{2} = 1\) となる。このとき \[ \begin{aligned} \phi'(t) & = -\frac{4t}{(1 + t^{2})^{2}},\quad \psi'(t) = \frac{2(1 - t^{2})}{(1 + t^{2})^{2}},\\ F'(t) & = -\frac{4t}{(1 + t^{2})^{2}}f_{x}' + \frac{2(1 - t^{2})}{(1 + t^{2})^{2}}f_{y}' \end{aligned} \] が成り立つ。この式では \(f\) を微分した後に \(x\) と \(y\) へ \(\dfrac{1 - t^{2}}{1 + t^{2}}\) と \(\dfrac{2t}{1 + t^{2}}\) を代入する。
具体的な値として例えば \(f(x, y) = x^{2} + y^{2}\) とすれば \(f_{x}' = 2x,\ f_{y}' = 2y\) となり、\(F'(t) = 2x\phi'(t) + 2y\psi'(t) = 0\) が分かる。\(F(t) = 1\) なので、これは明らかに正しい。
-
同じ要領で (a) \(x = t^{m},\ y = 1 - t^{m},\ f(x, y) = x + y\) および (b) \(x = a\cos t,\ y = a\sin t,\ f(x, y) = x^{2} + y^{2}\) に対して定理を確認せよ。
-
この定理の最も重要なインスタンスの一つが \(t\) が \(x\) に等しい場合である。このとき \[ D_{x}f\{x, \psi(x)\} = D_{x}f(x, y) + D_{y}f(x, y)\psi'(x) \] を得る。ここで \(y\) は微分した後に \(\psi(x)\) と置き換える。
\(\partial f/\partial x\) と \(\partial f/\partial y\) という記法の導入が正当化されるのは、この等式が成り立つためである。つまり \(df/dx\) は \(D_{x}f\{x, \psi(x)\}\) と \(D_{x}f(x, y)\) のどちらかに対して使うのが望ましい。\(D_{x}f\{x, \psi(x)\}\) では微分の前に \(y\) に \(\psi(x)\) を代入し、\(D_{x}f(x, y)\) では微分の後に代入する。例えば \(y = 1 - x\) および \(f(x, y) = x + y\) とすれば、\(D_{x}f(x, 1 - x) = D_{x}1 = 0\) に対して \(D_{x}f(x, y) = 1\) が成り立つ。
二つの関数の区別するために \(D_{x}f\{x, \psi(x)\}\) を \(df/dx\) と書き、\(D_{x}f(x, y)\) を \(\partial f/\partial x\) と書く。こう定めれば上記の定理は次のように表せる: \[ \frac{df}{dx} = \frac{\partial f}{\partial x} + \frac{\partial f}{\partial y}\, \frac{dy}{dx} \] ただこの記法にも問題がないわけではない。\(f\{x, \psi(x)\}\) と \(f(x, y)\) という二つの関数は \(x\) の関数としての形が全く異なっているにもかかわらず、\(df/dx\) と \(\partial f/\partial x\) では同じ記号 \(f\) を使って表されてしまっている。
-
\(x = \phi(t)\) と \(y = \psi(t)\) から \(t\) を削除した結果が \(f(x, y) = 0\) なら、 \[ \frac{\partial f}{\partial x}\, \frac{dx}{dt} + \frac{\partial f}{\partial y}\, \frac{dy}{dt} = 0 \] が成り立つ。
-
\(x\) と \(y\) が \(t\) の関数とする。\((x, y)\) の極座標を \((r, \theta)\) とすれば \(r' = (xx' + yy')/r\) および \(\theta' = (xy' - yx')/r^{2}\) が成り立つ。ダッシュは \(t\) に関する微分を表す。
§154 二変数関数の平均値の定理
前章の結果の多くは平均値の定理から導かれた。この定理は \[ \phi(x + h) - \phi(x) = hf'(x + \theta h) \] と表される。あるいは \(y = \phi(x)\) とすれば \[ \delta y = f'(x + \theta\, \delta x)\, \delta x \] とも書ける。
\(z = f(x, y)\) を二つの独立な変数 \(x\) と \(y\) の関数として、\(x\) と \(y\) の増分を \(h = \delta x\) および \(k = \delta y\) とする。\(z\) の増分 \[ \delta z = f(x + h, y + k) - f(x, y) \] を \(z\) の \(x\) と \(y\) に関する微分と \(h,\ k\) を使って表すことを考える。
\(f(x + ht, y + kt) = F(t)\) とすると、 \[ f(x + h, y + k) - f(x, y) = F(1) - F(0) = F'(\theta) \] となる \(\theta\ \) (\(0 \lt \theta \lt 1\)) が存在する。一方で §153 からは \[ \begin{aligned} F' (t) & = D_{t} f(x + ht, y + kt)\\ & = hf_{x}'(x + ht, y + kt) + kf_{y}'(x + ht, y + kt) \end{aligned} \] が分かり、二つの式から \[ \begin{aligned} \delta z & = f(x + h, y + k) - f(x, y) \\ & = hf_{x}'(x + \theta h, y + \theta k) + kf_{y}'(x + \theta h, y + \theta k) \end{aligned} \] が得られる。\(f_{x}'\) と \(f_{y}'\) は \(x\) と \(y\) の連続関数と仮定しているから、 \[ \begin{aligned} f_{x}'(x + \theta h, y + \theta k) & = f_{x}'(x, y) + \varepsilon_{h, k},\\ f_{y}'(x + \theta h, y + \theta k) & = f_{y}'(x, y) + \eta_{h, k} \end{aligned} \] とすれば \(h\) と \(k\) が \(0\) に向かうとき \(\varepsilon_{h, k}\) と \(\eta_{h, k}\) も \(0\) に向かう。よって上述の結果は \[ \delta z = (f_{x}' + \varepsilon)\, \delta x + (f_{y}' + \eta)\, \delta y \qquad \text{(1)} \] と書くことができる。ここで \(\delta x\) と \(\delta y\) が小さいとき \(\varepsilon\) と \(\eta\) も小さくなる。
\(\text{(1)}\) の結果を言い換えると「方程式 \[ \delta z = f_{x}'\, \delta x + f_{y}'\, \delta y \] が近似的に正しい」となる。つまり \(\delta x\) と \(\delta y\) の絶対値が大きい方7と比較するとこの式の両辺の差は小さい。ここで「\(\delta x\) と \(\delta y\) の絶対値の大きい方」と言わなければならないのは、\(\delta x\) と \(\delta y\) のどちらかがもう一方と比較して小さくなる場合があるためである。それどころか \(\delta x = 0\) あるいは \(\delta y = 0\) となるかもしれない。
\(\delta z = \lambda\, \delta x + \mu\, \delta y\) という形の方程式が今説明した意味で「近似的に」正しいなら \(\lambda = f_{x}',\ \mu = f_{y}'\) が成り立つことも示せる。仮定の式と (1) から \[ \delta z - f_{x}'\, \delta x - f_{y}'\, \delta y = \varepsilon\, \delta x + \eta\, \delta y,\quad \delta z - \lambda\, \delta x - \mu\, \delta y = \varepsilon'\, \delta x + \eta'\, \delta y \] が成り立ち、\(\delta x\) と \(\delta y\) が \(0\) に向かうとき \(\varepsilon,\ \eta,\ \varepsilon',\ \eta'\) は全て \(0\) に向かう。ここから \[ (\lambda - f_{x}')\, \delta x + (\mu - f_{y}')\, \delta y = \rho\, \delta x + \rho'\, \delta y \] とすれば \(\rho\) と \(\rho'\) も \(0\) に向かうと分かる。よって \(\zeta\) を任意の正の実数とすると、ある \(\sigma\) が存在して、絶対値が \(\sigma\) より小さい全ての \(\delta x\) と \(\delta y\) で \[ |(\lambda - f_{x}')\, \delta x + (\mu - f_{y}')\, \delta y| \lt \zeta(|\delta x| + |\delta y|) \] が成り立つ。\(\delta y = 0\) とすれば \(|(\lambda - f_{x}')\, \delta x| \lt \zeta|\delta x|\) つまり \(|\lambda - f_{x}'| \lt \zeta\) を得る。\(\zeta\) は好きなだけ小さくできるから、これは \(\lambda = f_{x}'\) でない限りあり得ない。同様に \(\mu = f_{y}'\) も示せる。
§155 微分小
微積分の応用、特に幾何学への応用では、§154 の式 \(\text{(1)}\) のような \(x,\ y,\ z\) の関数の増分 \(\delta x,\ \delta y,\ \delta z\) を使った式を使うよりも、\(dx,\ dy,\ dz\) で表される微分小 (differential) と呼ばれるものを使った式の方が便利な場合が多い。
しばらく一つの変数 \(x\) の関数 \(y = f(x)\) に話を戻す。\(f'(x)\) が連続なら、 \[ \delta y = \{f'(x) + \varepsilon\}\, \delta x \qquad \text{(1)} \] とすれば \(\delta x \to 0\) のとき \(\varepsilon \to 0\) が成り立つ。この事実を言い換えれば、等式 \[ \delta y = f'(x)\, \delta x \hphantom{\{{} + \varepsilon\}} \qquad \text{(2)} \] が「近似的に」正しい、ということになる。これまでは \(dy\) という単一の記号に意味を与えてこなかったが、ここで次の等式を使って \(dy\) を定義する: \[ dy = f'(x)\, \delta x \qquad \text{(3)} \]
\(x\) という具体的な関数を \(y\) として選べば \[ dx = \delta x \qquad \text{(4)} \] を得る。ここから \[ dy = f'(x)\, dx \qquad \text{(5)} \] が分かる。\(\text{(5)}\) の両辺を \(dx\) で割れば \[ \frac{dy}{dx} = f'(x) \qquad \text{(6)} \] となる。この \(dy/dx\) はこれまでのように \(y\) の微分係数を意味しているのではなく、二つの微分小の商を意味している。この結果として \(dy/dx\) という記号が二つの意味を持つことになったが、等式 \(\text{(6)}\) はどちらの意味であっても正しいので、何も問題は起こらない。
式 \(\text{(5)}\) には式 \(\text{(2)}\) と比べて二つの利点がある。まず \(\text{(5)}\) は近似ではなく正確な等式であり、その正しさに \(f'(x)\) の連続性が関係しない。反対に \(\text{(5)}\) の正確な等式から近似の等式 \(\text{(2)}\) へ変形が (特定の条件の下で) 可能であるというのは確実に言えるので、\(\text{(5)}\) がより重要となる。この「微分小」を使った記法の利点は純粋に技術的なものである。しかし特に複数の変数の関数を扱うときにこの技術的な利点が非常に大きくなるので、こういった記法の使用はまず避けられない。
\(f'(x)\) が連続なら、\(\delta x \to 0\) のとき \[ \lim \frac{dy}{\delta y} = 1 \] が成り立つ。この事実を指して「\(\delta x\) が小さいとき \(dy\) が \(\delta y\) の主部 (principal part) である」と表現することがある。「\(x\) が小さいとき \(ax\) は \(ax + bx^{2}\) の主部である」などと言うのと同様である。
これに対応する定義を二つの独立変数 \(x\) と \(y\) の関数 \(z\) に対しても考える。\(dz\) は次の等式で定義する: \[ dz = f_{x}'\, \delta x + f_{y}'\, \delta y \qquad \text{(7)} \] \(z = x\) および \(z = y\) を代入すれば \[ dx = \delta x,\quad dy = \delta y \qquad \text{(8)} \] が得られ、ここから \[ dz = f_{x}'\, dx + f_{y}'\, dy \qquad \text{(9)} \] が分かる。これは §154 の \(\text{(1)}\) に示した近似の式に対応する正確な形の等式と言える。ここでも同じ理由によりこの正確な等式が使われる。つまり実用上便利なことと、近似の式は正確な式から導けるというただそれだけの理由に過ぎない。
\(\text{(9)}\) には注目すべき性質が一つある。§153 で見たように、もし \(x\) と \(y\) が独立しておらず \(t\) という一つの変数の関数なら、\(z\) も \(t\) だけの関数であり \[ \frac{dz}{dt} = \frac{\partial f}{\partial x}\, \frac{dx}{dt} + \frac{\partial f}{\partial y}\, \frac{dy}{dt} \] が成り立つ。この等式の両辺に \(dt\) を乗じ、さらに \[ dx = \frac{dx}{dt}\, dt,\quad dy = \frac{dy}{dt}\, dt,\quad dz = \frac{dz}{dt}\, dt \] を使うと \[ dz = f_{x}'\, dx + f_{y}'\, dy \] が得られるが、これは \(\text{(9)}\) と同じ形をしている。つまり \(\bm{dz}\) を \(\bm{dx}\) と \(\bm{dy}\) で表した等式は、\(\bm{x}\) と \(\bm{y}\) が独立でも独立でなくても変わらない。この事実は応用において非常に重要となる。
また \(z\) が二つの独立変数 \(x\) と \(y\) の関数で \[ dz = \lambda\, dx + \mu\, dy \] なら \(\lambda = f_{x}',\ \mu = f_{y}'\) となることも分かる。§154 の最後の段落から容易に示せる。
ここまで三つの節を使って説明してきた定理や定義は、任意個数の変数の関数へと自明に拡張できる。
-
楕円の半軸を \(a,\ b\) とすると、面積は \(A = \pi ab\) で与えられる。 \[ \frac{dA}{A} = \frac{da}{a} + \frac{db}{b} \] を示し、さらに軸の増分と面積に関する近似的な等式を求めよ。
-
三角形 \(ABC\) の面積 \(\Delta\) を、(i) \(a,\ B,\ C,\ \) (ii) \(A,\ b,\ c,\ \) (iii) \(a,\ b,\ c\) の関数として表せ。さらに外接円の半径を \(R\) として \[ \begin{aligned} \frac{d\Delta}{\Delta} & = 2\frac{da}{a} + \frac{c\, dB}{a\sin B} + \frac{b\, dC}{a\sin C},\\ \frac{d\Delta}{\Delta} & = \cot A\, dA + \frac{db}{b} + \frac{dc}{c},\\ d\Delta & = R(\cos A\, da + \cos B\, db + \cos C\, dc) \end{aligned} \] を示せ。
-
三角形の面積を一定に保ったまま辺の長さを変化させるとき、\(a\) は \(b\) と \(c\) の関数とみなせる。このとき \[ \frac{\partial a}{\partial b} = -\frac{\cos B}{\cos A},\quad \frac{\partial a}{\partial c} = -\frac{\cos C}{\cos A} \] を示せ。
[等式 \[ da = \frac{\partial a}{\partial b}\, db + \frac{\partial a}{\partial c}\, dc,\quad \cos A\, da + \cos B\, db + \cos C\, dc = 0 \] から従う]
-
\(R\) を定数に保ったまま \(a,\ b,\ c\) が変化するなら \[ \frac{da}{\cos A} + \frac{db}{\cos B} + \frac{dc}{\cos C} = 0 \] が成り立ち、さらに \[ \frac{\partial a}{\partial b} = -\frac{\cos A}{\cos B},\quad \frac{\partial a}{\partial c} = -\frac{\cos A}{\cos C} \] となる。
[等式 \(a = 2R\sin A,\ \ldots\) と \(R\) および \(A + B + C\) が定数である事実を使う]
-
\(z\) が \(u\) と \(v\) の関数で、\(u\) と \(v\) が \(x\) と \(y\) の関数とする。このとき \[ \frac{\partial z}{\partial x} = \frac{\partial z}{\partial u}\, \frac{\partial u}{\partial x} + \frac{\partial z}{\partial v}\, \frac{\partial v}{\partial x},\quad \frac{\partial z}{\partial y} = \frac{\partial z}{\partial u}\, \frac{\partial u}{\partial y} + \frac{\partial z}{\partial v}\, \frac{\partial v}{\partial y} \] が成り立つ。
[仮定から \[ dz = \frac{\partial z}{\partial u}\, du + \frac{\partial z}{\partial v}\, dv,\quad du = \frac{\partial u}{\partial x}\, dx + \frac{\partial u}{\partial y}\, dy,\quad dv = \frac{\partial v}{\partial x}\, dx + \frac{\partial v}{\partial y}\, dy \] が分かる。最初の等式の \(du\) と \(dv\) に後ろの二つの等式を代入し、 \[ dz = \frac{\partial z}{\partial x}\, dx + \frac{\partial z}{\partial y}\, dy \] と比較すれば求めたい式が得られる]
-
\(z\) を \(x\) と \(y\) の関数として、\(X,\ Y,\ Z\) を次の等式で定義する: \[ x = a_{1} X + b_{1} Y + c_{1} Z,\quad y = a_{2} X + b_{2} Y + c_{2} Z,\quad z = a_{3} X + b_{3} Y + c_{3} Z \] このとき \(Z\) は \(X\) と \(Y\) の関数として表せる。\(\partial Z/\partial X\) と \(\partial Z/\partial Y\) を \(\partial z/\partial x\) と \(\partial z/\partial y\) を使って表せ。 [これらの微分係数を \(P,\ Q\) および \(p,\ q\) と表記する。このとき \(dz - p\, dx - q\, dy = 0\) であり、ここから \[ (c_{1} p + c_{2} q - c_{3})\, dZ + (a_{1} p + a_{2} q - a_{3})\, dX + (b_{1} p + b_{2} q - b_{3})\, dY = 0 \] が分かる。これを \(dZ - P\, dX - Q\, dY = 0\) と比較すれば \[ P = -\frac{a_{1}p + a_{2}q - a_{3}}{c_{1}p + c_{2}q - c_{3}},\quad Q = -\frac{b_{1}p + b_{2}q - b_{3}}{c_{1}p + c_{2}q - c_{3}} \] を得る]
-
前問の設定に加えて \[ (a_{1} x + b_{1} y + c_{1} z)p + (a_{2} x + b_{2} y + c_{2} z)q = a_{3} x + b_{3} y + c_{3} z \] が成り立つなら \[ (a_{1} X + b_{1} Y + c_{1} Z) P + (a_{2} X + b_{2} Y + c_{2} Z) Q = a_{3} X + b_{3} Y + c_{3} Z \] である。
(Math. Trip. 1899.)
-
陰関数の微分: \(f(x, y)\) と \(f_{y}'(x, y)\) が点 \((a, b)\) の近傍で連続とする。さらに \[ f(a, b) = 0,\quad f_{b}'(a, b) \neq 0 \] なら、\(f_{y}'(x, y)\) の符号が同一な \((a, b)\) の近傍が存在する。例として \(f_{y}'(x, y)\) が \((a, b)\) の近くで正である場合を考える。このとき \(a\) に十分近い \(x\) と \(b\) に十分近い \(y\) で \(f(x, y)\) は \(y\) の狭義単調増加関数となる (§96)。よって §108 の定理から、\(x = a\) では \(b\) に等しく \(x\) が \(a\) に近いときには等式 \(f(x, y) = 0\) が成り立つような連続関数 \(y\) が存在する。
さらに \(f(x, y)\) が \((a, b)\) の近傍で連続な \(f_{x}'(x, y)\) を持つとする。このとき \(f(x, y) = 0,\ x = a + h,\ y = b + k\) とすれば \[ 0 = f(x, y) - f(a, b) = (f_{a}' + \varepsilon) h + (f_{b}' + \eta) k \] であり、\(h\) と \(k\) が \(0\) に向かうとき \(\varepsilon\) と \(\eta\) は \(0\) に向かう。よって \[ \frac{k}{h} = -\frac{f_{a}' + \varepsilon}{f_{b}' + \eta} \to -\frac{f_{a}'}{f_{b}'} \] つまり \[ \frac{dy}{dx} = -\frac{f_{a}'}{f_{b}'} \] が成り立つ。
-
曲線 \(f(x, y) = 0\) 上の点 \((x_{0}, y_{0})\) における接線の方程式は \[ (x - x_{0}) f_{x_{0}}'(x_{0}, y_{0}) + (y - y_{0}) f_{y_{0}}'(x_{0}, y_{0}) = 0 \] である。
§156 定積分と面積
第六章の §145 では、\(PQ\) を \(x\) の連続関数 \(f(x)\) のグラフとしたとき 図 47 における領域 \(PpqQ\) に面積と呼ばれる値が定義されることを仮定して話を進めた。\(Op\) と \(Oq\) を \(a\) と \(x\) して \(x\) を変化させると、明らかにこの面積は \(x\) の関数となる。この関数を \(F(x)\) と表す。
§145 ではこの仮定の下で \(F'(x) = f(x)\) を示し、この結果を使えば特定の曲線の面積を計算できることを示した。しかし面積 \(F(x)\) なる値が存在するという最初の仮定はまだ正当化されていない。
長方形には面積が存在し、その値がニ辺の長さの積として得られることを私たちは知っている。またユークリッドによって示された三角形や平行四辺形あるいは多角形の性質を使えば、そういった図形の面積の意味を定められる。しかし現在の私たちは、曲線で囲まれた図形の面積の直接的な定義を知らない。これから \(F(x)\) に定義を与え、面積の存在を証明する方法を示す8。

\(f(x)\) が区間 \([a, b]\) で連続として、\([a, b]\) を \(x_{0},\ x_{1},\ x_{2},\ \ldots,\ x_{n}\) という分割点を使って複数の小区間に分割する。ここで \[ a = x_{0} \lt x_{1} \lt \cdots \lt x_{n-1} \lt x_{n} = b \] とする。さらに区間 \([x_{\nu}, x_{\nu+1}]\) (およびその長さ) を \(\delta_{\nu}\) と表記し、\(m_{\nu}\) で \(\delta_{\nu}\) における \(f(x)\) の下限 (§102) を表す。そして \[ s = m_{0}\delta_{0} + m_{1}\delta_{1} + \cdots + m_{n}\delta_{n} = \sum m_{\nu}\delta_{\nu} \] と定める。
\(M\) を \([a, b]\) における \(f(x)\) の上限とすれば、明らかに \(s \leq M(b - a)\) が成り立つ。よって §80 の言葉を使えば、\(s\) の取る値の集まりは上に有界となる。この集まりの上限を \(j\) とすれば、\(j\) より大きい \(s\) の値は存在せず、\(j\) より小さい任意の数より大きい \(s\) の値が存在する。
同様に \(\delta_{\nu}\) における \(f(x)\) の上限を \(M_{\nu}\) として、和 \[ S = \sum M_{\nu}\delta_{\nu} \] を定義する。
\([a, b]\) における \(f(x)\) の下限を \(m\) とすれば \(S \geq m(b - a)\) が成り立つ。よって \(S\) が取る値は下に有界であり、下限 \(J\) を持つ。\(J\) より小さい \(S\) の値は存在せず、\(J\) より大きい任意の数より小さい \(S\) が存在する。
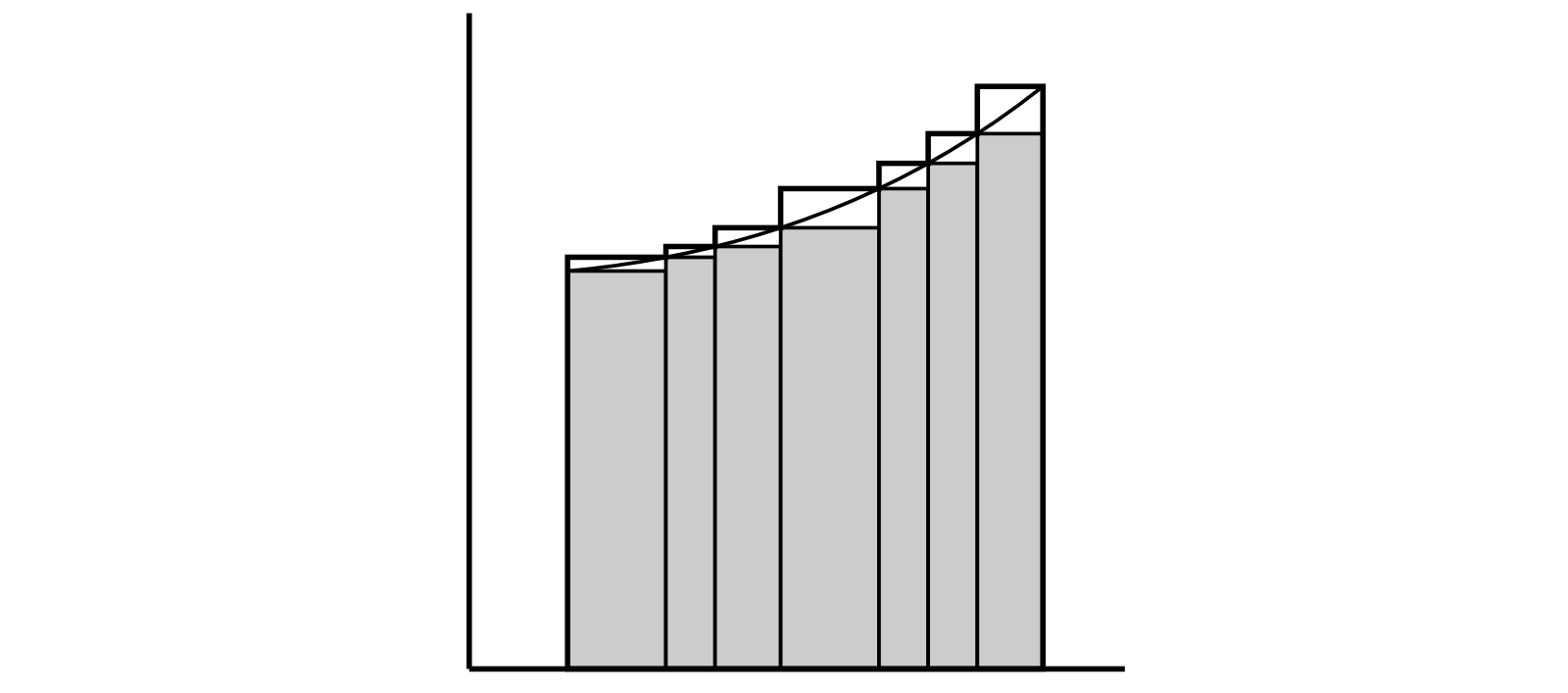
和 \(s\) と \(S\) の意味を理解するために、\(f(x)\) が \(x = a\) から \(x = b\) まで単調に増加するなら \(m_{\nu} = f(x_{\nu})\) かつ \(M_{\nu} = f(x_{\nu + 1})\) が成り立つことを納得しておくとよい。このとき 図 48 で灰色になっている長方形の面積の和が \(s\) で、太線で囲まれた領域の面積が \(S\) となる。一般に \(s\) と \(S\) は長方形からなる領域であり、面積を定義しようとしている曲線で囲まれた領域は \(s\) を含み、\(S\) に含まれる。
任意の和 \(\bm{s}\) が任意の和 \(\bm{S}\) よりも小さくなることを示す。ある分割に対応する和を \(s,\ S\) として、もう一つの適当な分割に対応する和を \(s',\ S'\) とする。\(s \leq S'\) と \(s' \leq S\) を示す必要がある。
\(s,\ S\) と \(s',\ S'\) に対応する二つの分割の分割点を全て取ることで、新しい分割を定義できる。この分割に対応する和を \(\mathbf{s},\ \mathbf{S}\) とすれば、明らかに \[ \mathbf{s} \geq s,\quad \mathbf{s} \geq s',\quad \mathbf{S} \leq S,\quad \mathbf{S} \leq S' \qquad \text{(1)} \] が成り立つ。例えば \(\mathbf{s}\) と \(s\) の違いを考えると、\(s\) に含まれる少なくとも一つの区間 \(\delta_{\mu}\) は、\(\mathbf{s}\) においていくつかの小区間 \[ \delta_{\nu, 1},\ \delta_{\nu, 2},\ \ldots,\ \delta_{\nu, p} \] に分割される。そのため \(s\) の \(m_{\nu}\delta_{\nu}\) という項は \(\mathbf{s}\) では \[ m_{\nu, 1}\delta_{\nu, 1} + m_{\nu, 2}\delta_{\nu, 2} + \cdots + m_{\nu, p}\delta_{\nu, p} \] という和になる。ここで \(m_{\nu, 1},\ m_{\nu, 2},\ \ldots\) は \(\delta_{\nu, 1},\ \delta_{\nu, 2},\ \ldots\) における \(f(x)\) の下限を表す。明らかに \(m_{\nu, 1} \geq m_{\nu},\ m_{\nu, 2} \geq m_{\nu},\ \ldots\) なので、この和は \(m_{\nu}\delta_{\nu}\) 以上である。よって \(\mathbf{s} \geq s\) が分かる。\(\text{(1)}\) の他の不等式も同様に示せる。さらに \(\mathbf{s} \leq \mathbf{S}\) だから、 \[ s \leq \mathbf{s} \leq \mathbf{S} \leq S' \] が分かる。これが証明すべきことだった。
また \(j \leq J\) も分かる。\(j\) に好きなだけ近い \(s\) と \(J\) に好きなだけ近い \(S\) を見つけられる9ので、\(j \gt J\) が成り立つなら \(s \gt S\) となる \(s\) と \(S\) が存在してしまう。
ここまでは \(f(x)\) が連続という事実を使ってこなかった。続いて \(j = J\) を示すときにこの事実を使う。区間 \(\delta_{\nu}\) の長さが \(0\) になるように分割点 \(x_{\nu}\) を増やしていくと、和 \(s\) および \(S\) が極限 \(J\) に向かうことも示す。より正確に言うと、任意の正の実数 \(\varepsilon\) に対して、全ての \(\nu\) で \(\delta_{\nu} \lt \delta\) なら \[ 0 \leq J - s \lt \varepsilon,\quad 0 \leq S - J \lt \varepsilon \] となる \(\delta\) が見つけられることを示す。
§106 の定理 2 から、ある \(\delta\) が存在して、全ての \(\delta_{\nu}\) が \(\delta\) より小さいなら \[ M_{\nu} - m_{\nu} \lt \frac{\varepsilon}{b - a} \] が成り立つ。よって \[ S - s = \sum (M_{\nu} - m_{\nu})\, \delta_{\nu} \lt \varepsilon \] となる。一方 \[ S - s = (S - J) + (J - j) + (j - s) \] であり、右辺の三項は全て正なので、この三項は全て \(\varepsilon\) より小さい。\(J - j\) は定数だから、\(0\) でなければならない。すなわち \(j = J\) かつ \(0 \leq j - s \lt \varepsilon,\ 0 \leq S - J \lt \varepsilon\) であり、示すべき関係が証明された。
領域 \(PpqQ\) の面積を \(\bm{s}\) と \(\bm{S}\) の共通の極限 \(\bm{J}\) として定義する。この定義にはより一般的で簡単な形が存在する。次の和を考える: \[ \sigma = \sum f_{\nu}\delta_{\nu} \] ここで \(f_{\nu}\) は \(\delta_{\nu}\) の適当な点における \(f(x)\) の値とする。\(\sigma\) は \(s\) と \(S\) の間にあるので、\(\delta_{\nu}\) が \(0\) に向かうとき極限 \(J\) に向かう。よって領域 \(PpqQ\) の面積を \(\sigma\) の極限として定義できる。
§157 定積分
\(f(x)\) を連続関数とすると、曲線 \(y = f(x)\) と \(x\) 軸と二つの垂直な直線 \(x = a\) と \(x = b\) で囲まれる領域は有限の領域となる。第六章の §145 で示したように、\(F(x)\) が \(f(x)\) の「積分関数」のとき、つまり \[ F'(x) = f(x),\quad F(x) = \int f(x)\, dx \] のとき、この領域の面積は \(F(b) - F(a)\) となる。
\(F(x)\) を表す式の計算がいつでも可能なわけではないので、\(F(x)\) を明示せずに \(PpqQ\) の面積を表現する方法があれば便利である。そこで \[ (PpqQ) = \int_{a}^{b} f(x)\, dx \] と書くことにする。
この等式の右辺の式は二つの方法のどちらかで定義されているとみなせる。まず \(f(x)\) を積分した関数の一つ \(F(x)\) に対する \(F(b) - F(a)\) の省略形と考える方法がある。ここで \(F(x)\) を示す式が計算できていなくても構わない。あるいは §156 で直接定義される \(PpqQ\) の面積と考えてもよい。
実数 \[ \int_{a}^{b} f(x)\, dx \] を定積分 (definite integral) と呼ぶ。\(a\) は積分の下端 (lower limit) と呼ばれ、\(b\) は積分の上端 (upper limit)、\([a, b]\) は積分区間 (range of integration) と呼ばれる。定積分は \(a\) と \(b\) そして関数 \(f(x)\) だけに依存しており、\(x\) の関数ではない。不定積分に対応する形で、関数の積分 \[ F(x) = \int f(x)\, dx \] を \(f(x)\) の不定積分 (indefinite integral) と呼ぶことがある。
定積分と不定積分の違いは観察する視点の違いに過ぎない。定積分 \(\displaystyle\int_{a}^{b} f(x)\, dx = F(b) - F(a)\) は \(b\) の関数であり、\(f(b)\) という関数のとある不定積分ともみなせる。あるいは不定積分 \(F(x)\) は常に定積分を使って表せる: \[ F(x) = F(a) + \int_{a}^{x} f(t)\, dt \]
ただ「不定積分」や「積分関数」を考えるときには、片方がもう一方の導関数であるという二つの関数の関係を考える場合が多い。そして「定積分」を考えるときには、積分する区間の変動を通常は考えない。区間は \(0\) から \(1\) のような定数であることが多く、この場合には \[ \int_{0}^{1} f(x)\, dx = F(1) - F(0) \] は関数ではなく、ただの実数となる。
\(\displaystyle\int_{a}^{x} f(t)\, dt\) は導関数に \(f(x)\) を持つので、間違いなく \(x\) の連続関数となる。
\(1/x\) は全ての正の \(x\) で連続なので、ここまでの議論から関数 \(\log x\) が本当に存在することが証明できる。§128 ではこの存在を仮定していた。
§158 扇形の面積と三角関数
\(\cos x\) や \(\sin x\) をはじめとした三角関数の理論が初等三角法の教科書で説明されるときには、証明されない仮定が最初におかれる場合が多い。二つの直線 \(OA\) と \(OP\) は角度 (angle) を定めるが、この「幾何学的な」定義を純粋に解析的な用語として採用することに問題はない。問題はこの次の、角度は数値として表せるという仮定にある。つまりここでは、図 47 の領域 \(PpqQ\) に対応する実数の存在と同じように、二つの直線の位置関係に対応する実数 \(x\) の存在が仮定されている。この点さえ認めれば、後は \(\cos x\) や \(\sin x\) が通常通りに定義でき、以降の理論の構築で行き詰まることもない。つまり唯一の問題は \(\bm{\cos x}\) や \(\bm{\sin x}\) における \(\bm{x}\) とはいったい何なのかにある。この問題を解決するには角度の意味を定める必要があり、私たちはこれからこれを行う。最も自然な定義は次のようになる: \(O\) を中心とした半径 \(1\) の円の弧を \(AP\) とすれば \(OA = OP = 1\) が成り立つ。そして角度の大きさを表す実数 \(x\) を 弧 \(\bm{AP}\) の長さと定める。この定義はたいていの教科書で採用されるものであり、"弧度法" の理論がここから展開される。しかし今の目的に照らして考えると致命的な欠陥がある。曲線の長さは面積と同じように詳細な数学的な解析が可能な概念であり、その解析はこれまでの節と似てはいるものの明らかにより難しい。そのため曲線の長さをここで一般的に扱うなどとてもできない。
つまり長さではなく面積を使って角度を定義しなければならない。そこで \(\angle AOP\) を 単位円上の扇形 \(\bm{AOP}\) の面積の二倍として定義する。
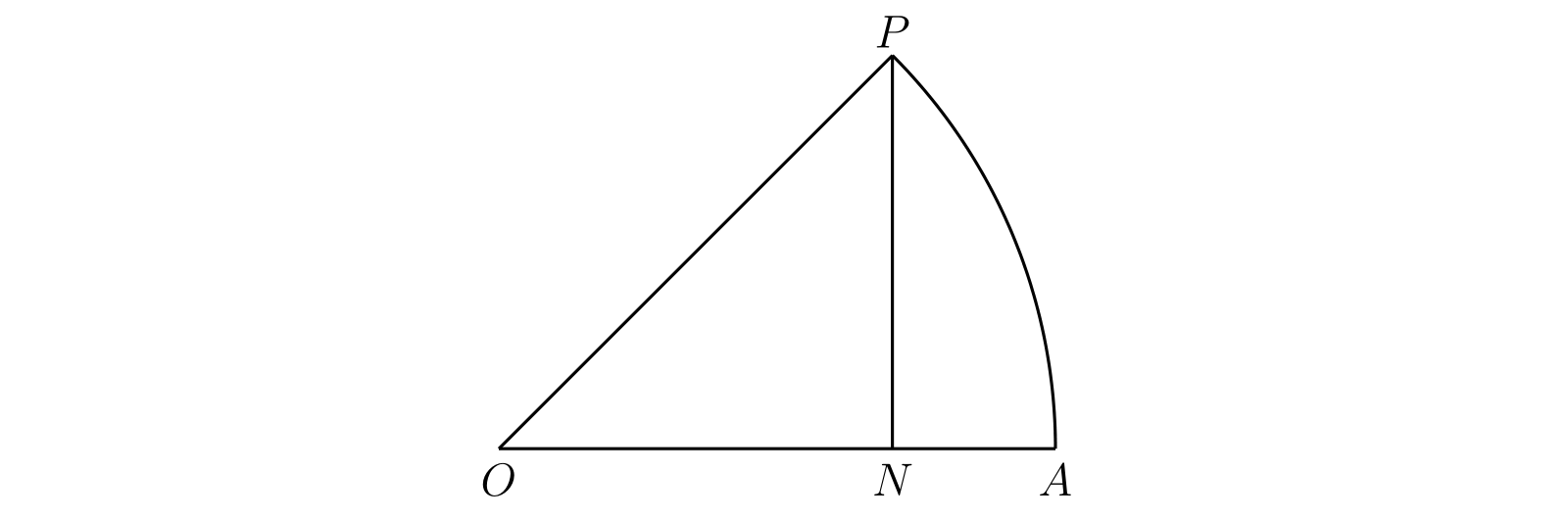
\(OA\) が \(y = 0\) で \(OP\) が \(y = mx\) である場合を考える (\(m \gt 0\))。扇形の面積は \(m\) の関数だから、これを \(\phi(m)\) と表す。\(\mu = (1 + m^{2})^{-\frac{1}{2}}\) とすれば \(P\) は点 \((\mu, m\mu)\) となり \[ \phi(m) = \dfrac{1}{2} m\mu^{2} + \int_{\mu}^{1} \sqrt{1 - x^{2}}\, dx \] が成り立つ。これを \(m\) で微分すれば \[ \phi'(m) = \frac{1}{2(1 + m^{2})},\quad \phi(m) = \dfrac{1}{2} \int_{0}^{m} \frac{dt}{1 + t^{2}} \] が分かる。よって先ほどの面積を使った角度の定義を解析的に表すには、\(\arctan m\) を等式 \[ \arctan m = \int_{0}^{m} \frac{dt}{1 + t^{2}} \] で定義すればよいと分かる。三角関数に関する理論はこの等式を始点として全て構築できる。第九章では同様の方法で対数の理論を得る。補遺 三 も参照。
不定積分を使った定積分の計算
-
次を示せ: \[ \int_{a}^{b} x^{n}\, dx = \frac{b^{n+1} - a^{n+1}}{n + 1} \] ここから特に \[ \int_{0}^{1} x^{n}\, dx = \frac{1}{n + 1} \] が分かる。
-
\(\displaystyle\int_{a}^{b} \cos mx\, dx = \frac{\sin mb - \sin ma}{m},\quad \displaystyle\int_{a}^{b} \sin mx\, dx = \frac{\cos ma - \cos mb}{m}\)
-
\(\displaystyle\int_{a}^{b}\frac{dx}{1 + x^{2}} = \arctan b - \arctan a,\quad \displaystyle\int_{0}^{1}\frac{dx}{1 + x^{2}} = \dfrac{1}{4}\pi\)
[一見すると多価関数 \(\arctan x\) が関係する積分は込み入って見えるが、等式 \[ \int_{0}^{x} \frac{dt}{1 + t^{2}} = \arctan x \] において \(\arctan x\) の表す角度が必ず \(-\frac{1}{2}\pi\) と \(\frac{1}{2}\pi\) の間にある事実が分かれば難しくない。この事実は \(x = 0\) で積分が \(0\) であり、\(x\) と共に単調増加することから分かる。つまり \(\arctan x\) も単調増加で、\(x \to \infty\) のとき \(\frac{1}{2}\pi\) に向かう。同様に \(x \to -\infty\) なら \(\arctan x \to -\frac{1}{2}\pi\) だとも示せる。同様に \(-1 \lt x \lt 1\) に対する等式 \[ \int_{0}^{x} \frac{dt}{\sqrt{1 - t^{2}}} = \arcsin x \] からは、角度 \(\arcsin x\) が \(-\frac{1}{2}\pi\) と \(\frac{1}{2}\pi\) の間にあることが分かる。よってもし \(a\) と \(b\) の絶対値が \(1\) 未満なら \[ \int_{a}^{b} \frac{dx}{\sqrt{1 - x^{2}}} = \arcsin b - \arcsin a \] が成り立つ]
-
\(\displaystyle\int_{0}^{1} \frac{dx}{1 - x + x^{2}} = \frac{2\pi}{3\sqrt3},\quad\displaystyle\int_{0}^{1} \frac{dx}{1 + x + x^{2}} = \frac{\pi}{3\sqrt3}\)
-
\(-\pi \lt \alpha \lt \pi\) なら \(\displaystyle\int_{0}^{1} \frac{dx}{1 + 2x\cos\alpha + x^{2}} = \frac{\alpha}{2\sin\alpha}\) が成り立つ。ただし \(\alpha = 0\) では \(\dfrac{1}{2}\) で、これは \(\alpha \to 0\) における \(\dfrac{1}{2}\alpha\cosec\alpha\) の極限に等しい。
-
\(\displaystyle\int_{0}^{1} \sqrt{1 - x^{2}}\, dx = \dfrac{1}{4}\pi,\quad \displaystyle\int_{0}^{a} \sqrt{a^{2} - x^{2}}\, dx = \dfrac{1}{4}\pi a^{2}\quad \) \((a \gt 0)\)
-
\(a \gt |b|\) なら \(\displaystyle\int_{0}^{\pi} \frac{dx}{a + b\cos x} = \frac{\pi}{\sqrt{a^{2} - b^{2}}}\) が成り立つ。 [不定積分の形については 例 53.3, 4 を参照。\(|a| \lt |b|\) だと \(0\) と \(\pi\) の間で被積分関数が無限大になる。\(a\) が負で \(-a \gt |b|\) のときの積分の値はどうなるか?]
-
\(a\) と \(b\) が正なら \(\displaystyle\int_{0}^{\frac{1}{2}\pi} \frac{dx}{a^{2}\cos^{2}x + b^{2}\sin^{2}x} = \frac{\pi}{2ab}\) が成り立つ。\(a\) と \(b\) が異なる符号を持つとき、あるいは両方負のときの積分の値は何か?
-
フーリエ積分: \(m\) と \(n\) を正の整数としたとき、 \[ \int_{0}^{2\pi} \cos mx \sin nx\, dx \] が常に \(0\) に等しいこと、および \[ \int_{0}^{2\pi} \cos mx \cos nx\, dx,\quad \int_{0}^{2\pi} \sin mx \sin nx\, dx \] が \(m = n\) なら \(\pi\) でそれ以外のとき \(0\) となることを示せ。
-
\(\displaystyle\int_{0}^{\pi} \cos mx \cos nx\, dx\) と \(\displaystyle\int_{0}^{\pi} \sin mx \sin nx\, dx\) が \(m = n\) なら \(\frac{1}{2}\pi\) で、そうでないなら \(0\) だと示せ。さらに \(n - m\) が奇数か偶数かに応じて \[ \int_{0}^{\pi} \cos mx \sin nx\, dx = \frac{2n}{n^{2} - m^{2}},\quad \int_{0}^{\pi} \cos mx \sin nx\, dx = 0 \] だと示せ。
§159 和の極限を使った定義による定積分の計算
§156–§157 で示した定義を使って定積分を直接計算できる場合も少数だがある。一般に不定積分を使って計算した方がずっと簡単なことが多いが、いくつか例を計算すれば理解が深まるだろう。
-
\(\displaystyle\int_{a}^{b} x\, dx\) を計算せよ。分割点 \(a = x_{0},\ x_{1},\ x_{2},\ \ldots,\ x_{n} = b\) で \([a, b]\) を \(n\) 等分し、 \[ (x_{1} - x_{0})f(x_{0}) + (x_{2} - x_{1})f(x_{1}) + \cdots + (x_{n} - x_{n-1})f(x_{n-1}) \] の \(n \to \infty\) における極限として求めること。
[和は \[ \small \begin{aligned} & \frac{b - a}{n}\left[ a + \left(a + \frac{b - a}{n}\right) + \left(a + 2\frac{b - a}{n}\right) + \cdots + \left\{a + (n - 1)\frac{b - a}{n}\right\} \right]\\ & \quad = \frac{b - a}{n}\left[ na + \frac{b - a}{n} \{1 + 2 + \cdots + (n - 1)\} \right]\\ & \quad = (b - a)\left\{a + (b - a)\frac{n(n - 1)}{2n^{2}}\right\} \end{aligned} \] であり、\(n \to \infty\) のとき極限 \(\frac{1}{2} (b^{2} - a^{2})\) に向かう。この結果を幾何学的に確認するとよい]
-
同様の方法で \(\displaystyle\int_{a}^{b} x^{2}\, dx\) を計算せよ。
-
\(\displaystyle\int_{a}^{b} x\, dx\) (\(0 \lt a \lt b\)) を計算せよ。\(r^{n} = b/a\) として \(a,\ ar,\ ar^{2},\ \ldots,\ ar^{n-1},\ ar^{n}\) という分割点で \([a, b]\) を \(n\) 個の部分に分割する方法を使うこと。
-
問題 1 の方法を使って \(\displaystyle\int_{a}^{b}\cos mx\, dx\) と \(\displaystyle\int_{a}^{b}\sin mx\, dx\) を計算せよ。
-
\(n \to \infty\) で \(n\sum\limits_{r=0}^{n-1} \dfrac{1}{n^{2} + r^{2}} \to \dfrac{1}{4}\pi\) だと示せ。
[次の等式から分かる: \[ \frac{n}{n^{2}} + \frac{n}{n^{2} + 1^{2}} + \cdots + \frac{n}{n^{2} + (n - 1)^{2}} = \sum_{r=0}^{n-1} \frac{(1/n)}{1 + (r/n)^{2}} \] 積分の直接的な定義から、\(n \to \infty\) におけるこの式の極限は \(\displaystyle\int_{0}^{1} \frac{dx}{1 + x^{2}}\) となる]
-
\(\dfrac{1}{n^{2}} \sum\limits_{r=0}^{n-1} \sqrt{n^{2} - r^{2}} \to \dfrac{1}{4}\pi\) を示せ。 [左辺の極限は \(\displaystyle\int_{0}^{1} \sqrt{1 - x^{2}}\, dx\) となる]
§160 定積分の性質
定積分は次に示す重要な性質を持つ10。
-
\(\displaystyle\int_{a}^{b} f(x)\, dx = -\int_{b}^{a} f(x)\, dx\)
これは \(F(x)\) を使った積分の定義から直ちに従う。つまり \(F(b) - F(a) = -\{F(a) - F(b)\}\) である。和を使った直接的な定義では上端が下端より大きいことが仮定されており、この定義は \(a \lt b\) のときの \(\displaystyle\int_{b}^{a} f(x)\, dx\) に適用できない。和を使った定義を基礎的なものとみなすなら、等式 \(\text{(1)}\) を右辺の定義とみなして定義を拡張する必要がある。
-
\(\displaystyle\int_{a}^{a} f(x)\, dx = 0\)
-
\(\displaystyle\int_{a}^{b}f(x)\, dx + \int_{b}^{c}f(x)\, dx = \int_{a}^{c}f(x)\, dx\)
-
\(\displaystyle\int_{a}^{b}kf(x)\, dx = k \int_{a}^{b}f(x)\, dx\)
-
\(\displaystyle\int_{a}^{b}\{f(x) + \phi(x)\}\, dx = \int_{a}^{b}f(x)\, dx + \int_{a}^{b}\phi(x)\, dx\)
こういった性質のきちんとした証明を書けば積分の理解が深まるだろう。不定積分を使った定義と和を使った直接的な定義の両方から示すとよい。次の関係も重要である:
-
\(a \leq x \leq b\) で \(f(x) \geq 0\) なら \(\displaystyle\int_{a}^{b}f(x)\, dx \geq 0\) が成り立つ。
§156 の和 \(s\) が負にならないと示すだけで済む。第七章に関するその他の例 41 ではこの条件の下では \(f(x)\) が常に \(0\) でない限り積分が \(0\) にならないことを示す。この事実は §121 の系 2 からも示せる。
-
\(a \leq x \leq b\) で \(H \leq f(x) \leq K\) なら次が成り立つ: \[ H(b - a) \leq \int_{a}^{b}f(x)\, dx \leq K(b - a) \]
\(f(x) - H\) と \(K - f(x)\) に対して \(\text{(6)}\) を適用すれば直ちに得られる。
-
\(a\) と \(b\) の間にある \(\xi\) で \(\displaystyle\int_{a}^{b}f(x)\, dx = (b-a)f(\xi)\) が成り立つ。
これは \(\text{(7)}\) を使えば示せる。\([a, b]\) における \(f(x)\) の最大値を \(H\) として最小値を \(K\) とすれば、積分の値は \(H\) と \(K\) の間の値 \(\eta\) を使って \(\eta(b - a)\) となる。\(f(x)\) は連続だから、\(f(\xi) = \eta\) を満たす \(\xi\) が存在する (§100)。
\(f(x)\) の不定積分を \(F(x)\) とすれば、\(\text{(8)}\) は \[ F(b) - F(a) = (b - a)F'(\xi) \] と書ける。つまり \(\text{(8)}\) は §125 で説明した平均値の定理の別表現である。\(\text{(8)}\) の等式を積分に対する平均値の定理 (First Mean Value Theorem for Integrals) と呼ぶ。
-
積分に対する一般化された平均値の定理: \(\phi(x)\) が \([a, b]\) で常に正だとする。\(\text{(7)}\) と同じように \(H\) と \(K\) を定めると、 \[ H\int_{a}^{b} \phi(x)\, dx \leq \int_{a}^{b} f(x)\phi(x)\, dx \leq K\int_{a}^{b} \phi(x)\, dx \] および \[ \int_{a}^{b} f(x)\phi(x)\, dx = f(\xi) \int_{a}^{b} \phi(x)\, dx \] が成り立つ。ここで \(\xi\) は \(\text{(8)}\) と同様とする。
\(\text{(6)}\) を次の積分に対して適用すれば得られる: \[ \int_{a}^{b} \{f(x) - H\}\phi(x)\, dx,\quad \int_{a}^{b} \{K - f(x)\}\phi(x)\, dx \] \(\phi(x)\) が常に負である場合に対応する結果を自分で書いてみるとよい。
-
積分の基本定理: 関数 \[ F(x) = \int_{a}^{x} f(t)\, dt \] の導関数は \(f(x)\) に等しい。
これは前に §145 で示したが、ここできちんと述べておいた方がいいだろう。§157 でも指摘したように、この系として \(\bm{F(x)}\) は \(\bm{x}\) の連続関数だと分かる。
-
和を使った直接的な定積分の定義と上述の結果 \(\text{(1)}\) – \(\text{(5)}\) を使って次を示せ:
- \(\displaystyle\int_{-a}^{a} \phi(x^{2})\, dx = 2\int_{0}^{a} \phi(x^{2})\, dx,\quad \displaystyle\int_{-a}^{a} x\phi(x^{2})\, dx = 0\)
- \(\displaystyle\int_{0}^{\frac{1}{2}\pi} \phi(\cos x)\, dx = \int_{0}^{\frac{1}{2} \pi} \phi(\sin x)\, dx = \dfrac{1}{2} \int_{0}^{\pi} \phi(\sin x)\, dx\)
- \(\displaystyle\int_{0}^{m\pi} \phi(\cos^{2} x)\, dx = m\int_{0}^{\pi} \phi(\cos^{2} x)\, dx\quad \) (\(m\) は整数)
[積分記号の中にある関数のグラフを描けば、これらの結果は幾何学的に分かる]
-
積分 \(\displaystyle\int_{0}^{\pi} \frac{\sin nx}{\sin x}\, dx\) の値は \(n\) が奇数のとき \(\pi\) で \(n\) が偶数のとき \(0\) だと示せ。 [等式 \((\sin nx)/(\sin x) = 2\cos \{(n - 1)x\} + 2\cos \{(n - 3)x\} + \cdots\) を使う。最後の項が \(1\) または \(2\cos x\) となる]
-
積分 \(\displaystyle\int_{0}^{\pi} \sin nx \cot x\, dx\) の値は \(n\) が奇数のとき \(0\) で \(n\) が偶数のとき \(\pi\) だと示せ。
-
\(\phi(x) = a_{0} + a_{1}\cos x + b_{1}\sin x + a_{2}\cos 2x + \cdots + a_{n}\cos nx + b_{n}\sin nx\) とする。\(n\) 以下の正の整数 \(k\) に対して \[ \int_{0}^{2\pi} \phi(x)\, dx = 2\pi a_{0},\ {} \int_{0}^{2\pi} \cos kx \phi(x)\, dx = \pi a_{k},\ {} \int_{0}^{2\pi} \sin kx \phi(x)\, dx = \pi b_{k} \] だと示せ。\(k \gt n\) なら後ろの二つの積分の値は \(0\) となる。 [例 63.9 を使う]
-
\(\phi(x) = a_{0} + a_{1} \cos x + a_{2}\cos 2x + \cdots + a_{n}\cos nx\) とする。\(n\) 以下の正の整数 \(k\) に対して \[ \int_{0}^{\pi} \phi(x)\, dx = \pi a_{0},\quad \int_{0}^{\pi} \cos kx \phi(x)\, dx = \dfrac{1}{2}\pi a_{k} \] だと示せ。\(k \gt n\) なら最後の積分の値は \(0\) となる。 [例 63.10 を使う]
-
\(a\) と \(b\) が正なら \[ \int_{0}^{2\pi} \frac{dx}{a^{2}\cos^{2} x + b^{2}\sin^{2} x} = \frac{2\pi}{ab} \] だと示せ。[例 63.8 とこの例の問題 1 を使う]
-
\(a \leq x \leq b\) で \(f(x) \leq \phi(x)\) なら \(\displaystyle\int_{a}^{b} f\, dx \leq \int_{a}^{b}\phi\, dx\) が成り立つ。
-
次を示せ: \[ \begin{alignedat}{2} 0 & \lt \int_{0}^{\frac{1}{2}\pi} \sin^{n+1}x\, dx & & \lt \int_{0}^{\frac{1}{2}\pi} \sin^{n}x\, dx,\\ 0 & \lt \int_{0}^{\frac{1}{4}\pi} \tan^{n+1}x\, dx & & \lt \int_{0}^{\frac{1}{4}\pi} \tan^{n}x\, dx \end{alignedat} \]
-
\(n \gt 1\) なら次の不等式が成り立つ11: \[ .5 \lt \int_{0}^{\frac{1}{2}} \frac{dx}{\sqrt{1 - x^{2n}}} \lt .524 \]
[\(\sqrt{1 - x^{2n}} \lt 1\) と \(\sqrt{1 - x^{2n}} \gt \sqrt{1 - x^{2}}\) から分かる]
-
次を示せ: \[ \dfrac{1}{2} \lt \int_{0}^{1} \frac{dx}{\sqrt{4 - x^{2} + x^{3}}} \lt \dfrac{1}{6}\pi \]
-
\(0 \lt x \lt 1\) なら \(\dfrac{3x + 8}{16} \lt \dfrac{1}{\sqrt{4 - 3x + x^{3}}} \lt \dfrac{1}{\sqrt{4 - 3x}}\) だと示し、そこから次を示せ: \[ \dfrac{19}{32} \lt \int_{0}^{1} \frac{dx}{\sqrt{4 - 3x + x^{3}}} \lt \dfrac{2}{3} \]
-
次を示せ: \[ .573 \lt \int_{1}^{2} \frac{dx}{\sqrt{4 - 3x + x^{3}}} \lt .595 \]
[\(x = 1 + u\) として、\(2 + 3u^{2} + u^{3}\) を \(2 + 4u^{2}\) および \(2 + 3u^{2}\) と置き換える]
-
\(\alpha\) と \(\phi\) を正の鋭角とする。このとき \[ \phi \lt \int_{0}^{\phi} \frac{dx}{\sqrt{1 - \sin^{2}\alpha \sin^{2} x}} \lt \frac{\phi}{\sqrt{1 - \sin^{2}\alpha \sin^{2}\phi}} \] が成り立つ。もし \(\alpha = \phi = \frac{1}{6}\pi\) なら、積分の値は \(.523\) と \(.541\) の間にある。
-
次を示せ: \[ \left|\int_{a}^{b} f(x)\, dx\right| \leq \int_{a}^{b}|f(x)|\, dx \]
[§156 の最後で考えた和 \(\sigma\) について、\(|f(x)|\) に対応する同じ和 \(\sigma'\) を考えれば \(|\sigma| \leq \sigma'\) が成り立つ]
-
\(|f(x)| \leq M\) のとき次の不等式が成り立つ: \[ \left|\int_{a}^{b} f(x)\phi(x)\, dx\right| \leq M\int_{a}^{b}|\phi(x)|\, dx \]
§161 置換積分と部分積分
§138 から \[ \int_{a}^{b} f(x)\phi'(x)\, dx = f(b)\phi(b) - f(a)\phi(a) - \int_{a}^{b} f'(x)\phi(x)\, dx \] が分かる。この等式は部分定積分 (integration of a definite integral by parts) の公式という名前で知られる。
同様に §133 からは、\(f(t)\) の不定積分が \(F(t)\) なら \[ \int f\{\phi(x)\}\phi'(x)\, dx = F\{\phi(x)\} \] だと分かる。よって \(\phi(a) = c,\ \phi(b) = d\) とすれば \[ \int_{c}^{d} f(t)\, dt = F(d) - F(c) = F\{\phi(b)\} - F\{\phi(a)\} = \int_{a}^{b} f\{\phi(x)\}\phi'(x)\, dx \] を得る。これは置換 (substitution) を使った定積分の変形公式である。
部分積分と置換積分の公式を使うと、被積分関数の不定積分をわざわざ計算せずとも定積分の値を求められる場合がある。そればかりか、不定積分がそもそも求められない場合でも値が求まることもある。この例を次の例でいくつか示す。不定積分を知らなくても定積分の値が求められる場合があるのは不思議なことではない。不定積分 \(F(x)\) の一般的な形が求められなくても、二つの特定の値の差 \(F(b) - F(a)\) なら求められる可能性がまだ残っている。ただ一般的に、この方法による計算は現在の私たちが知っているよりも高度な手法を使ってはじめて可能となる。
-
次を示せ: \[ \int_{a}^{b} x f''(x)\, dx = \{bf'(b) - f(b)\} - \{af'(a) - f(a)\} \]
-
より一般的には \[ \int_{a}^{b} x^{m} f^{(m+1)}(x)\, dx = F(b) - F(a) \] なら次が成り立つ: \[ \begin{aligned} F(x) = {} & x^{m} f^{(m)}(x) - mx^{m-1} f^{(m-1)}(x) \\ & \quad + m(m - 1)x^{m-2} f^{(m-2)}(x) - \cdots + (-1)^{m} m!\, f(x) \end{aligned} \]
-
次を示せ: \[ \int_{0}^{1} \arcsin x\, dx = \dfrac{1}{2}\pi - 1,\quad \int_{0}^{1}x\arctan x\, dx = \dfrac{1}{4}\pi - \dfrac{1}{2} \]
-
\(a\) と \(b\) が正のとき次を示せ: \[ \int_{0}^{\frac{1}{2}\pi} \frac{x\cos x\sin x\, dx}{(a^{2}\cos^{2}x + b^{2}\sin^{2}x)^{2}} = \frac{\pi}{4ab^{2}(a + b)} \]
[部分積分をしてから 例 63.8 を使う]
-
もし \[ f_{1}(x) = \int_{0}^{x}f(t)\, dt,\quad f_{2}(x) = \int_{0}^{x}f_{1}(t)\, dt,\ \ldots,\quad f_{k}(x) = \int_{0}^{x} f_{k-1}(t)\, dt \] なら次が成り立つ: \[ f_{k}(x) = \frac{1}{(k - 1)!} \int_{0}^{x} f(t)(x - t)^{k-1}\, dt \]
[部分積分を繰り返し使う]
-
\(m\) と \(n\) を正の整数とする。 \[ u_{m, n} = \int_{0}^{1} x^{m} (1 - x)^{n}\, dx \] なら \((m + n + 1) u_{m, n} = nu_{m, n-1}\) だと示し、次の等式を導け: \[ u_{m, n} = \frac{m!\, n!}{(m + n + 1)!} \]
-
\(\displaystyle u_{n} = \int_{0}^{\frac{1}{4}\pi} \tan^{n}x\, dx\) なら \(u_{n} + u_{n-2} = \dfrac{1}{n - 1}\) だとを示せ。これを使って全ての正の整数 \(n\) に対する積分の値を計算せよ。
[\(\tan^{n}x = \tan^{n-2}x(\sec^{2}x - 1)\) を使い、それから部分積分する]
-
前問の結果を使って \(u_{n}\) が \(\dfrac{1}{2(n - 1)}\) と \(\dfrac{1}{2(n + 1)}\) の間にあると示せ。
-
\(\displaystyle u_{n} = \int_{0}^{\frac{1}{2}\pi} \sin^{n} x\, dx\) なら \(u_{n} = \dfrac{n - 1}{n} u_{n-2}\) だと示せ。 [\(\sin^{n}x\) を \(\sin^{n-1}x\sin x\) として部分積分する]
-
\(n\) が奇数なら \[ u_{n} = \frac{2·4·6 \cdots (n - 1)}{3·5·7 \cdots n} \] で、\(n\) が偶数なら \[ u_{n} = \dfrac{1}{2}\pi \frac{1·3·5 \cdots (n - 1)}{2·4·6 \cdots n} \] だと示せ。
-
第二の平均値の定理 (Second Mean Value Theorem): \(x\) の関数 \(f(x)\) が \(x = a\) から \(x = b\) の間で符号が一定な微分係数を持つとする。このとき \(a\) と \(b\) の間のとある \(\xi\) で \[ \int_{a}^{b} f(x)\phi(x)\, dx = f(a) \int_{a}^{\xi} \phi(x)\, dx + f(b) \int_{\xi}^{b} \phi(x)\, dx \] が成り立つ。
[\(\Phi(x) = \displaystyle\int_{a}^{x}\phi(t)\, dt\) とすると、§160 で示した一般化された平均値の定理から \[ \begin{aligned} \int_{a}^{b} f(x)\phi(x)\, dx & = \int_{a}^{b} f(x)\Phi'(x)\, dx \\ & = f(b)\Phi(b) - \int_{a}^{b} f'(x)\Phi(x)\, dx\\ & = f(b)\Phi(b) - \Phi(\xi) \int_{a}^{b}f'(x)\, dx \end{aligned} \] が分かる。ここから示したい結果と同値な式 \[ \int_{a}^{b} f(x)\phi(x)\, dx = f(b)\Phi(b) + \{f(a) - f(b)\}\Phi(\xi) \] が得られる]
-
ボネによって発見された第二の平均値の定理の別表現: \(f'(x)\) の符号が一定で、\(f(b)\) と \(f(a) - f(b)\) が同じ符号を持つとする。このとき \(a\) と \(b\) の間のとある \(X\) で \[ \int_{a}^{b} f(x)\phi(x)\, dx = f(a) \int_{a}^{X} \phi(x)\, dx \] が成り立つ。 [仮定より \(f(b)\Phi(b) + \{f(a) - f(b)\}\Phi(\xi) = \mu f(a)\) が \(\Phi(\xi)\) と \(\Phi(b)\) の間のとある \(\mu\) で成り立つから、\(\mu = \Phi(x)\) となる \(x\) を \(X\) として取れる。特に重要なのは \(0 \leq f(b) \leq f(x) \leq f(a)\) の場合である]
同様に \(f(a)\) と \(f(b) - f(a)\) が同じ符号を持つなら、\(a\) と \(b\) のとある \(X\) で \[ \int_{a}^{b} f(x)\phi(x)\, dx = f(b) \int_{X}^{b} \phi(x)\, dx \] が成り立つ。 [関数 \(\Psi(\xi) = \displaystyle\int_{\xi}^{b} \phi(x)\, dx\) を使う。積分は \[ f(a)\Psi(a) + \{f(b) - f(a)\}\Psi(\xi) \] となる。特に重要なのは \(0 \leq f(a) \leq f(x) \leq f(b)\) の場合である]
-
\(X' \gt X \gt 0\) なら \(\displaystyle \left|\int_{X}^{X'} \frac{\sin x}{x}\, dx\right| \lt \frac{2}{X}\) だと示せ。
[問題 12 の最初の等式を適用する。\(\sin x\) の任意の区間に渡る積分の絶対値が \(2\) より小さいことに注意する]
-
例 65.1 の結果を置換積分を使って示せ。 [(i) では積分区間を \([-a, 0]\) と \([0, a]\) に分割して、一つ目の積分で \(x = -y\) とする。(ii) では置換 \(x = \frac{1}{2}\pi - y\) から一つ目の等式が得られ、二つ目の等式では \([0, \pi]\) を二等分してから \(x = \frac{1}{2}\pi + y\) を使う。(iii) では積分区間を \(m\) 等分して \(x = \pi + y,\ x = 2\pi + y,\ \ldots\) を使う]
-
\(\displaystyle \int_{a}^{b} F(x)\, dx = \int_{a}^{b} F(a + b - x)\, dx\) を示せ。
-
\(\displaystyle \int_{0}^{\frac{1}{2}\pi} \cos^{m} x\sin^{m} x\, dx = 2^{-m} \int_{0}^{\frac{1}{2}\pi} \cos^{m} x\, dx\) を示せ。
-
\(\displaystyle \int_{0}^{\pi} x\phi(\sin x)\, dx = \dfrac{1}{2}\pi \int_{0}^{\pi} \phi(\sin x)\, dx\) を示せ。
[\(x = \pi - y\) とする]
-
\(\displaystyle \int_{0}^{\pi} \frac{x\sin x}{1 + \cos^{2} x}\, dx = \dfrac{1}{4}\pi^{2}\) を示せ。
-
変形 \(x = a\cos^{2}\theta + b\sin^{2}\theta\) を使って次を示せ: \[ \int_{a}^{b} \sqrt{(x - a)(b - x)}\, dx = \dfrac{1}{8}\pi (b - a)^{2} \]
-
置換 \((a + b\cos x) (a - b\cos y) = a^{2} - b^{2}\) を使って、\(n\) が正の整数で \(a \gt |b|\) なら \[ \int_{0}^{\pi} (a + b\cos x)^{-n}\, dx = (a^{2} - b^{2})^{-(n - \frac{1}{2})} \int_{0}^{\pi} (a - b\cos y)^{n-1}\, dy \] だと示せ。\(n = 1,\ 2,\ 3\) に対する積分の値を求めよ。
-
\(m\) と \(n\) が正の整数なら次が成り立つ: \[ \int_{a}^{b} (x - a)^{m} (b - x)^{n}\, dx = (b - a)^{m+n+1} \frac{m!\, n!}{(m + n + 1)!} \]
[\(x = a + (b - a)y\) として問題 6 を使う]
§162 部分積分を使ったテイラーの定理の証明
続いて §147 で予告したテイラーの定理の別証明を示す。
\(n\) 次までの導関数が連続な関数を \(f(x)\) として、\(F_{n}(x)\) を次のように定める: \[ F_{n}(x) = f(b) - f(x) - (b - x)f'(x) - \cdots - \frac{(b - x)^{n-1}}{(n - 1)!} f^{(n-1)}(x) \]
このとき \[ F_{n}'(x) = -\frac{(b - x)^{n-1}}{(n - 1)!} f^{(n)}(x) \] であり、ここから \[ F_{n}(a) = F_{n}(b) - \int_{a}^{b}F_{n}'(x)\, dx = \frac{1}{(n - 1)!} \int_{a}^{b} (b - x)^{n-1} f^{(n)}(x)\, dx \] が分かる。\(b\) を \(a + h\) と書き、\(x = a + th\) として積分を変形すると \[ f(a + h) = f(a) + hf'(a) + \cdots + \frac{h^{n-1}}{(n - 1)!} f^{(n-1)}(a) + R_{n} \qquad \text{(1)} \] を得る。ここで \(R_{n}\) は次のようになる: \[ R_{n} = \frac{h^{n}}{(n - 1)!} \int_{0}^{1} (1 - t)^{n-1} f^{(n)}(a + th)\, dt \qquad \text{(2)} \]
\(p\) を \(n\) 以下の正の整数とすると、§160 の結果 (9) から \[ \begin{aligned} \int_{0}^{1} (1 - t)^{n-1} f^{(n)}(a + th)\, dt & = \int_{0}^{1}(1 - t)^{n-p} (1 - t)^{p-1} f^{(n)}(a + th)\, dt \\ & = (1 - \theta)^{n-p} f^{(n)}(a + \theta h) \int_{0}^{1} (1 - t)^{p-1}\, dt \end{aligned} \] が \(\theta\ \) (\(0 \lt \theta \lt 1\)) で成り立つ。よって次の式が得られる: \[ R_{n} = \frac{(1 - \theta)^{n-p} f^{(n)}(a + \theta h)h^{n}}{p(n - 1)!} \qquad \text{(3)} \]
\(p = n\) とすればラグランジュの剰余項 \(R_{n}\) (§148) となる12。一方で \(p = 1\) とすれば、コーシーの剰余項と呼ばれる次の形が得られる: \[ R_{n} = \frac{(1 - \theta)^{n-1} f^{(n)}(a + \theta h) h^{n}}{(n - 1)!} \qquad \text{(4)} \]
§163 コーシーの剰余項の二項係数への応用
\(m\) が正の整数でないとする。このとき \(f(x) = (1 + x)^{m}\) に対するコーシーの剰余項は次のようになる: \[ R_{n} = \frac{m(m - 1)\cdots (m - n + 1)}{1·2\cdots (n - 1)}\, \frac{(1 - \theta )^{n-1} x^{n}}{(1 + \theta x)^{n-m}} \]
ここで \(-1 \lt x \lt 1\) なら、\(x\) が正でも負でも \((1 - \theta)/(1 + \theta x)\) は \(1\) より小さい。さらに全ての \(n\) に対して \((1 + \theta x)^{m-1}\) は定数 \(K\) より小さくなる。具体的には \(m \gt 1\) なら \((1 + |x|)^{m-1}\) より小さく、\(m \lt 1\) なら \((1 - |x|)^{m-1}\) より小さい。したがって \[ |R_{n}| \lt K |m| \left|\binom{m - 1}{n - 1}\right| |x^{n}| = \rho_{n} \] とすれば、例 27.13 より \(n \to \infty\) で \(\rho_{n} \to 0\) となる。よって \(R_{n} \to 0\) が分かる。以上で全ての有理数 \(m\) と \(-1\) から \(1\) の間の \(x\) に対する二項定理が証明された。ラグランジュの剰余項を使った 例 56.2 では負の \(x\) の扱いが困難だったことを思い出してほしい。
§164 実変数の複素関数の積分
ここまで定積分の被積分関数は実関数だとしてきた。実変数 \(x\) の複素関数 \(f(x) = \phi(x) + i\psi(x)\) の \(a\) から \(b\) までの間の積分は次のように定義する: \[ \int_{a}^{b} f(x)\, dx = \int_{a}^{b} \{\phi(x) + i\psi(x)\}\, dx = \int_{a}^{b} \phi(x)\, dx + i \int_{a}^{b} \psi(x)\, dx \] この積分がこれまでに考えた実関数の積分と変わらない性質を持つことは明らかに分かる。
そのような性質の中に以降で使うことになるものが一つある。その性質は次の不等式で表される13: \[ \left|\int_{a}^{b} f(x)\, dx\right| \leq \int_{a}^{b} |f(x)|\, dx \qquad \text{(1)} \] この不等式は §156–§157 の定義から容易に示せる。\(\delta_{\nu}\) が §156 と同じ意味を持ち、\(\delta_{\nu}\) の適当な点における \(\phi\) と \(\psi\) の値を \(\phi_{\nu}\) と \(\psi_{\nu}\) とする。さらに \(f_{\nu} = \phi_{\nu} + i\psi_{\nu}\) とすれば \[ \begin{aligned} \int_{a}^{b} f\, dx & = \int_{a}^{b} \phi\, dx + i \int_{a}^{b} \psi\, dx \\ & = \lim \sum \phi_{\nu}\, \delta_{\nu} + i \lim \sum \psi_{\nu}\, \delta_{\nu} \\ & = \lim \sum (\phi_{\nu} + i\psi_{\nu})\, \delta_{\nu} = \lim \sum f_{\nu}\, \delta_{\nu} \end{aligned} \] であり、ここから \[ \left|\int_{a}^{b} f\, dx\right| = \left|\lim \sum f_{\nu}\, \delta_{\nu}\right| = \lim \left|\sum f_{\nu}\, \delta_{\nu}\right| \] が分かる。さらに \[ \int_{a}^{b} |f|\, dx = \lim \sum |f_{\nu}|\, \delta_{\nu} \] だから、求めたい不等式は \[ \left|\sum f_{\nu}\, \delta_{\nu}\right| \leq \sum |f_{\nu}|\, \delta_{\nu} \] から容易に示せる。
§162 の式 \(\text{(1)}\) と \(\text{(2)}\) が \(f\) が複素関数 \(\phi + i\psi\) の場合にも成り立つことも分かる。
第七章に関するその他の例
-
次のテイラー級数を確認せよ: \[ \begin{alignedat}{2} & \text{(1)} & \tan x & = x + \dfrac{1}{3} x^{3} + \dfrac{2}{15} x^{5} + \cdots, \\ & \text{(2)} & \sec x & = 1 + \dfrac{1}{2} x^{2} + \dfrac{5}{24} x^{4} + \cdots, \\ & \text{(3)}\quad & x\cosec x & = 1 + \dfrac{1}{6} x^{2} + \dfrac{7}{360} x^{4} + \cdots, \\ & \text{(4)} & x\cot x & = 1 - \dfrac{1}{3} x^{2} - \dfrac{1}{45} x^{4} - \cdots \end{alignedat} \]
-
\(f(x)\) とその \(n + 2\) 次までの導関数が連続で \(f^{(n+1)}(0) \neq 0\) とする。第 \(n\) 項までのテイラー級数のラグランジュの剰余項における \(\theta\) の値を \(\theta_{n}\) とすると、 \[ \theta_{n} = \frac{1}{n + 1} + \frac{n}{2(n + 1)^{2}(n + 2)} \left\{\frac{f^{(n+2)}(0)}{f^{(n+1)}(0)} + \varepsilon_{x}\right\}x \] が成り立つ。ただし \(x \to 0\) で \(\varepsilon_{x} \to 0\) とする。 [例 55.12 と同じ方法を使う]
-
\(f(x) = \dfrac{1}{1 + x}\) として前問の結果を確認せよ。 [\((1 + \theta_{n}x)^{n+1} = 1 + x\) となる]
-
\(f(x)\) が三次までの導関数を持つとする。このとき \[ f(b) = f(a) + \dfrac{1}{2}(b - a) \{f'(a) + f'(b)\} - \dfrac{1}{12}(b - a)^{3} f'''(\alpha) \] を示せ。ここで \(a \lt \alpha \lt b\) とする。 [関数 \[ \begin{aligned} & f(x) - f(a) - \dfrac{1}{2}(x - a) \{f'(a) + f'(x)\}\\ & \qquad - \left(\frac{x - a}{b - a}\right)^{3} [f(b) - f(a) - \dfrac{1}{2}(b - a) \{f'(a) + f'(b)\}] \end{aligned} \] に §147 と同様の議論を適用する]
-
前問と同じ条件で次を示せ: \[ f(b) = f(a) + (b - a) f'\{\dfrac{1}{2}(a + b)\} + \dfrac{1}{24}(b - a)^{3}f'''(\alpha) \]
-
同様に \(f(x)\) が五次までの導関数を持つとき次の等式が成り立つと示せ: \[ \begin{aligned} f(b) = f(a) & + \dfrac{1}{6}(b - a) [f'(a) + f'(b) + 4f'\{\dfrac{1}{2}(a + b)\}] \\ & - \dfrac{1}{2880}(b - a)^{5} f^{(5)}(\alpha) \end{aligned} \]
-
同じ条件で次を示せ: \[ \begin{aligned} f(b) = f(a) & + \dfrac{1}{2}(b - a) \{f'(a) + f'(b)\} \\ & - \dfrac{1}{12}(b - a)^{2} \{f''(b) - f''(a)\} + \dfrac{1}{720}(b - a)^{5} f^{(5)}(\alpha) \end{aligned} \]
-
次の等式を示せ:
- \(\displaystyle \begin{vmatrix} f(a) & f(b)\\ g(a) & g(b) \end{vmatrix} = (b - a) \begin{vmatrix} f(a) & f'(\beta)\\ g(a) & g'(\beta) \end{vmatrix}\)
\(\beta\) は \(a\) と \(b\) の間にあるとする。
- \(\displaystyle\begin{vmatrix} f(a) & f(b) & f(c)\\ g(a) & g(b) & g(c)\\ h(a) & h(b) & h(c)\end{vmatrix}= \dfrac{1}{2} (b - c)(c - a)(a - b)\begin{vmatrix} f(a) & f'(\beta) & f''(\gamma)\\ g(a) & g'(\beta) & g''(\gamma)\\ h(a) & h'(\beta) & h''(\gamma)\end{vmatrix}\)
\(\beta\) と \(\gamma\) は \(a,\ b,\ c\) の最小値と最大値の間にあるとする。
[(ii) の証明では、関数 \[ \phi(x) = \begin{vmatrix} f(a) & f(b) & f(x)\\ g(a) & g(b) & g(x)\\ h(a) & h(b) & h(x) \end{vmatrix} - \frac{(x - a)(x - b)}{(c - a)(c - b)} \begin{vmatrix} f(a) & f(b) & f(c)\\ g(a) & g(b) & g(c)\\ h(a) & h(b) & h(c) \end{vmatrix} \] を考える。この関数は \(x = a\) と \(x = b\) と \(x = c\) で \(0\) になる。§121 の定理 B から、\(a,\ b,\ c\) の最小値と最大値の間の二つの \(x\) で \(\phi(x)\) の一次導関数が \(0\) になること、さらに同じく \(a,\ b,\ c\) の最小値と最大値の間にある一つの \(\gamma\) で \(\phi(x)\) の二次導関数が \(0\) になることが分かる。ここから \[ \begin{vmatrix} f(a) & f(b) & f(c)\\ g(a) & g(b) & g(c)\\ h(a) & h(b) & h(c) \end{vmatrix} = \dfrac{1}{2}(c - a)(c - b) \begin{vmatrix} f(a) & f(b) & f''(\gamma)\\ g(a) & g(b) & g''(\gamma)\\ h(a) & h(b) & h''(\gamma) \end{vmatrix} \] を得る。残りの証明は易しい]
- \(\displaystyle \begin{vmatrix} f(a) & f(b)\\ g(a) & g(b) \end{vmatrix} = (b - a) \begin{vmatrix} f(a) & f'(\beta)\\ g(a) & g'(\beta) \end{vmatrix}\)
-
\(F(x)\) の \(n\) 次までの導関数が連続で、\(n - 1\) 次までの導関数は \(x = 0\) で \(0\) になるとする。これに加えて \(0 \leq x \leq h\) のとき \(A \leq F^{(n)}(x) \leq B\) なら、\(0 \leq x \leq h\) で \(A(x^{n}/n!) \leq F(x) \leq B(x^{n}/n!)\) だと示せ。
この結果を \[ f(x) - f(0) - xf'(0) - \cdots - \frac{x^{n-1}}{(n - 1)!} f^{(n-1)}(0) \] に適用し、テイラーの定理を導け。
-
\(\Delta_{h}\phi(x) = \phi(x) - \phi(x + h),\ \Delta_{h}^{2}\phi(x) = \Delta_{h}\{\Delta_{h}\phi(x)\},\ \ldots\) とする。\(\phi(x)\) が \(n\) 次までの導関数を持つなら \[ \Delta_{h}^{n}\phi(x) = \sum_{r=0}^{n}(-1)^{r} \binom{n}{r} \phi(x + rh) = (-h)^{n} \phi^{(n)}(\xi) \] が成り立つ。ここで \(\xi\) は \(x\) と \(x + nh\) の間にあるとする。さらに \(\phi^{(n)}(x)\) が連続なら、\(h \to 0\) で \(\{\Delta_{h}^{n}\phi(x)\}/h^{n} \to (-1)^{n}\phi^{(n)}(x)\) だと示せ。 [\(n = 2\) に対するこの結果は 例 55.13 で示した]
-
問題 10 を使って \(x \to \infty\) のとき \(x^{n-m}\, \Delta_{h}^{n} x^{m} \to m(m - 1) \cdots (m - n + 1)h^{n}\) だと示せ。\(m\) は任意の有理数で、\(n\) は任意の整数とする。これを使って次の式を証明せよ: \[ x\sqrt{x} \{\sqrt{x} - 2\sqrt{x + 1} + \sqrt{x + 2}\} \to -\dfrac{1}{4} \]
-
\(y = \phi(x)\) の導関数が少なくとも四次まで連続であり、\(\phi(0) = 0\) および \(\phi'(0) = 1\) が成り立つとする。このとき \(x \to 0\) で \(\varepsilon_{x} \to 0\) となる \(\varepsilon_{x}\) を使って \[ y = \phi(x) = x + a_{2}x^{2} + a_{3}x^{3} + (a_{4} + \varepsilon_{x})x^{4} \] とできる。次の等式を示せ: \[ x = \psi(y) = y - a_{2}y^{2} + (2a_{2}^{2} - a_{3})y^{3} - (5a_{2}^{3} - 5a_{2}a_{3} + a_{4} + \varepsilon_{y})y^{4} \] ただし \(y \to 0\) で \(\varepsilon_{y} \to 0\) とする。なおこのとき \(x\) も \(0\) に向かう。加えて \(x \to 0\) で \[ \frac{\phi(x)\psi(x) - x^{2}}{x^{4}} \to a_{2}^{2} \] だと示せ。
-
曲線 \(x = f(t),\ y = F(t)\) の曲率中心の座標 \((\xi, \eta)\) が \[ -\frac{\xi - x}{y'} = \frac{\eta - y}{x'} = \frac{{x'}^{2} + {y'}^{2}}{x'y'' - x''y'} \] で与えられ、曲率半径が \[ \frac{({x'}^{2} + {y'}^{2})^{3/2}}{x'y'' - x''y'} \] で与えられると示せ。ダッシュは \(t\) に関する微分を表す。
-
曲線 \(27ay^{2} = 4x^{3}\) 上の点 \((x, y)\) における曲率中心の座標 \((\xi, \eta)\) は \[ 3a(\xi + x) + 2x^{2} = 0, \quad \eta = 4y + \frac{9ay}{x} \] で与えられる。
(Math. Trip. 1899.)
-
曲線上の点 \((x, y)\) で \((1 + y_{1}^{2})y_{3} = 3y_{1}y_{2}^{2}\) が成り立つとき、\((x, y)\) における曲率円と曲線が三次の接触点を持つと示せ。さらに全ての点でこの性質を持つ唯一の曲線が円であること、この性質を持つ円錐曲線上の点が軸の端点のみであることを示せ。
-
\(y = ax^{2} + bx^{3} + cx^{4} + \cdots + kx^{n}\) と原点で交わる円錐曲線で接触点の次数が最も高いものは \(a^{3}y = a^{4}x^{2} + a^{2}bxy + (ac - b^{2})y^{2}\) である。この事実を使って、曲線 \(y = f(x)\) と \((\xi, \eta)\) で交わる円錐曲線で接触点の次数が最も高いものは \[ 18\eta_{2}^{3}T = 9\eta_{2}^{4}(x - \xi)^{2} + 6\eta_{2}^{2}\eta_{3}(x - \xi)T + (3\eta_{2}\eta_{4} - 4\eta_{3}^{2})T^{2} \] だと示せ。ここで \(T = (y - \eta) - \eta_{1}(x - \xi)\) とする。
(Math. Trip. 1907.)
-
同次関数14: \(u = x^{n} f(y/x, z/x,\ \ldots)\) とすると、\(x,\ y,\ z,\ \ldots\) が一定の比 \(\lambda : 1\) で増加するとき \(u\) の値は \(\lambda^{n}\) 倍になる以外は変化しない。このとき \(u\) を変数 \(x,\ y,\ z,\ \ldots\) に関する 次数 \(\bm{n}\) の同次関数 (homogeneous function of degree \(n\)) と呼ぶ。\(u\) が次数 \(n\) の同次関数なら \[ x\frac{\partial u}{\partial x} + y\frac{\partial u}{\partial y} + z\frac{\partial u}{\partial z} + \cdots = nu \] が成り立つことを示せ。この結果は同次関数に関するオイラーの定理と呼ばれる。
-
\(u\) が次数 \(n\) の同次関数なら、\(\dfrac{\partial u}{\partial x},\ \dfrac{\partial u}{\partial y},\ \ldots\) は次数 \(n - 1\) の同次関数である。
-
\(f(x, y) = 0\) を \(x\) と \(y\) に関する等式 (例えば \(x^{n} + y^{n} - x = 0\)) として、新しく変数 \(z\) を導入することで \(f(x, y)\) を同次にした等式 (例えば \(x^{n} + y^{n} - xz^{n-1} = 0\)) を \(F(x, y, z) = 0\) とする。曲線 \(f(x, y) = 0\) 上の 点 \((\xi, \eta)\) における接線の方程式が \[ xF_{\xi} + yF_{\eta} + zF_{\zeta} = 0 \] だと示せ。ここで \(F_{\xi},\ F_{\eta},\ F_{\zeta}\) は \(x = \xi,\ y = \eta,\ z = \zeta = 1\) における \(F_{x},\ F_{y},\ F_{z}\) の値を表す。
-
独立関数と従属関数 (ヤコビアンあるいは関数行列式): \(u\) と \(v\) が \(x\) と \(y\) の関数で、恒等的な関係 \[ \phi(u, v) = 0 \qquad \text{(1)} \] で結ばれているとする。
\(\text{(1)}\) を \(x\) および \(y\) に関して微分すると \[ \frac{\partial \phi}{\partial u}\, \frac{\partial u}{\partial x} + \frac{\partial \phi}{\partial v}\, \frac{\partial v}{\partial x} = 0,\quad \frac{\partial \phi}{\partial u}\, \frac{\partial u}{\partial y} + \frac{\partial \phi}{\partial v}\, \frac{\partial v}{\partial y} = 0 \qquad \text{(2)} \] を得る。ここから \(\phi\) の導関数を削除すると \[ J = \begin{vmatrix} u_{x} & u_{y}\\ v_{x} & v_{y} \end{vmatrix} = u_{x}v_{y} - u_{y}v_{x} = 0 \qquad \text{(3)} \] となる。ここで \(u_{x},\ u_{y},\ v_{x},\ v_{y}\) は \(u\) と \(v\) の \(x\) と \(y\) に関する導関数を表す。つまりこの条件は \(\text{(1)}\) を満たす関係が存在するための必要条件である。実はこの条件が十分でもあることが証明できる。詳細はグルサ著 Cours d' Analyse, vol. i, pp. 125 et seq. に譲る。
二つの関数 \(u\) と \(v\) が \(\text{(1)}\) の関係で結ばれているとき \(u\) と \(v\) は従属 (dependent)であると言い、そうでないなら独立 (independent) であると言う。\(J\) は \(x\) と \(y\) に関する \(u\) と \(v\) の ヤコビアン (Jacobian) あるいは関数行列式 (functional determinant) と呼ばれ、次のように表記される: \[ J = \frac{\partial(u, v)}{\partial(x, y)} \]
同様の結果は変数が任意個の関数でも成り立つ。例えば三変数 \(x,\ y,\ z\) に関する三つの関数 \(u,\ v,\ w\) が \(\phi(u, v, w) = 0\) という関係で結ばれるのは全ての \(x,\ y,\ z\) で \[ J = \begin{vmatrix} u_{x} & u_{y} & u_{z}\\ v_{x} & v_{y} & v_{z}\\ w_{x} & w_{y} & w_{z} \end{vmatrix} = \frac{\partial(u, v, w)}{\partial(x, y, z)} \] が \(0\) になるときで、そうでないなら \(u,\ v,\ w\) を結ぶ関係は存在しない。
-
\(ax^{2} + 2hxy + by_{2}\) と \(Ax^{2} + 2Hxy + By^{2}\) は \(\dfrac{a}{A} = \dfrac{h}{H} = \dfrac{b}{B}\) でない限り独立となる。
-
\(ax^{2} + by^{2} + cz^{2} + 2fyz + 2gzx + 2hxy\) が \(x,\ y,\ z\) の線形関数二つの積として表せるのは \[ abc + 2fgh - af^{2} - bg^{2} - ch^{2} = 0 \] が成り立つときに限ることを示せ。
[\(px + qy + rz\) と \(p'x + q'y + r'z\) が与えられた関数で結び付くための条件を関数の関係として書く]
-
\(u\) と \(v\) が \(\xi\) と \(\eta\) の関数で、さらに \(\xi\) と \(\eta\) が \(x\) と \(y\) の関数とする。このとき \[ \frac{\partial(u, v)}{\partial(x, y)} = \frac{\partial(u, v)}{\partial(\xi, \eta)}\, \frac{\partial(\xi, \eta)}{\partial(x, y)} \] が成り立つ。この結果を任意個の変数の場合に拡張せよ。
-
導関数が \(1/x\) であり \(x = 1\) で \(0\) となる関数を \(f(x)\) とする。\(u = f(x) + f(y)\) および \(v = xy\) とすれば \(u_{x}v_{y} - u_{y}v_{x} = 0\) であり、したがって \(u\) と \(v\) が何らかの関数の関係で結ばれることを示せ。さらに \(y = 1\) を代入し、この関係が \(f(x) + f(y) = f(xy)\) でなければならないと示せ。同様に \(f(x)\) の導関数が \(1/(1 + x^{2})\) で \(f(0) = 0\) なら、\(f(x)\) は \[ f(x) + f(y) = f\left(\frac{x + y}{1 - xy}\right) \] を満たさなければならないと示せ。
-
\(\displaystyle f(x) = \int_{0}^{x} \frac{dt}{\sqrt{1 - t^{4}}}\) のとき次を示せ: \[ f(x) + f(y) = f\left\{ \frac{x\sqrt{1 - y^{4}} + y\sqrt{1 - x^{4}}}{1 + x^{2}y^{2}} \right\} \]
-
関数の関係が \[ \begin{aligned} u & = f(x) + f(y) + f(z),\\ v & = f(y)f(z) + f(z)f(x) + f(x)f(y),\\ w & = f(x)f(y)f(z) \end{aligned} \] の間に存在するなら、\(f\) は定数だと示せ。 [関数の関係が存在するための条件は \[ f'(x)f'(y)f'(z) \{f(y) - f(z)\} \{f(z) - f(x)\} \{f(x) - f(y)\} = 0 \] となる]
-
\(f(y, z),\ f(z, x),\ f(x, y)\) が関数の関係で結ばれるなら、\(f(x, x)\) は \(x\) と独立である。
(Math. Trip. 1909.)
-
\(u = 0,\ v = 0,\ w = 0\) が三つの円の方程式で、問題 19 の方法で同次になっているとする。このとき \[ \frac{\partial(u, v, w)}{\partial(x, y, z)} = 0 \] は三つの円全てと直行する円を表す。
(Math. Trip. 1900.)
-
\(A,\ B,\ C\) が \(x\) の関数で、 \[ \begin{vmatrix} A & A' & A''\\ B & B' & B''\\ C & C' & C'' \end{vmatrix} \] が恒等的に \(0\) になるとする。このとき \(\lambda A + \mu B + \nu C\) が恒等的に \(0\) になるような定数 \(\lambda,\ \mu,\ \nu\) を見つけられる。逆も成り立つ。 [逆はほぼ自明である。順方向の命題を示すには、\(\alpha = BC' - B'C,\ \ldots\) とすると上の行列式が \(0\) より \(\beta\gamma' - \beta'\gamma = 0,\ \ldots\) となる事実を使う。ここから比 \(\alpha : \beta : \gamma\) が定数と分かるが、一方で \(\alpha A + \beta B + \gamma C = 0\) が成り立つ]
-
三つの変数 \(x,\ y,\ z\) がある関係で結ばれていて、\(z\) が \(x\) と \(y\) の関数で導関数 \(z_{x},\ z_{y}\) を持ち、\(x\) は \(y\) と \(z\) の関数で導関数 \(x_{y},\ x_{z}\) を持つとする。次を示せ: \[ x_{y} = - \frac{z_{y}}{z_{x}},\quad x_{z} = \frac{1}{z_{x}} \]
-
四つの変数 \(x,\ y,\ z,\ u\) が二つの関係で結ばれていて、どの二つも他の二つの関数として表せるとする。このとき \[ y_{z}^{u}z_{x}^{u}x_{y}^{u} = -y_{z}^{x}z_{x}^{y}x_{y}^{z} = 1,\quad x_{z}^{u}z_{x}^{y} + y_{z}^{u}z_{y}^{x} = 1 \] を示せ。\(y_{z}^{u}\) は \(z\) と \(u\) の関数として表した \(y\) の \(z\) に関する導関数を表す。
(Math. Trip. 1897.)
-
次の関数の四次までの導関数が \(x = 0\) で \(0\) になるような \(A,\ B,\ C,\ \lambda\) を求めよ: \[ \int_{a}^{a+x} f(t)\, dt - x[Af(a) + Bf(a + \lambda x) + Cf(a + x)] \] さらに次の関数の六次までの導関数が \(x = 0\) で \(0\) になるような \(A,\ B,\ C,\ D,\ \lambda,\ \mu\) を求めよ: \[ \int_{a}^{a+x} f(t)\, dt - x[Af(a) + Bf(a + \lambda x) + Cf(a + \mu x) + Df(a + x)] \]
-
\(a \gt 0,ac - b^{2} \gt 0\) かつ \(x_{1} \gt x_{0}\) とする。このとき \[ \int_{x_{0}}^{x_{1}} \frac{dx}{ax^{2} + 2bx + c} = \frac{1}{\sqrt{ac - b^{2}}} \arctan\left\{ \frac{(x_{1} - x_{0}) \sqrt{ac - b^{2}}} {ax_{1}x_{0} + b(x_{1} + x_{0}) + c} \right\} \] が成り立つ。タンジェントの逆関数は \(0\) から \(\pi\) の値を取るとする15。
-
積分 \(\displaystyle\int_{-1}^{1} \frac{\sin\alpha\, dx}{1 - 2x\cos\alpha + x^{2}}\) を計算せよ。\(\alpha\) の関数としてのこの積分が不連続となる \(\alpha\) の値は何か?
(Math. Trip. 1904.)
[積分は \(n\) を整数として \(2n\pi \lt \alpha \lt (2n + 1)\pi\) なら \(\frac{1}{2}\pi\)、\((2n - 1)\pi \lt \alpha \lt 2n\pi\) なら \(-\frac{1}{2}\)、\(\alpha\) が \(\pi\) の倍数なら \(0\) となる]
-
\(x_{0} \leq x \leq x_{1}\) で \(ax^{2} + 2bx + c \gt 0\) が成り立つとする。\(f(x) = \sqrt{ax^{2} + 2bx + c}\) および \[ y = f(x),\quad y_{0} = f(x_{0}),\quad y_{1} = f(x_{1}),\quad X = \frac{x_{1} - x_{0}}{y_{1} + y_{0}} \] とすると、\(a\) の正負に応じて \[ \int_{x_{0}}^{x_{1}} \frac{dx}{y} = \frac{1}{\sqrt{a}} \log \frac{1 + X\sqrt{a}}{1 - X\sqrt{a}},\quad \frac{-2}{\sqrt{-a}} \arctan\{X\sqrt{-a}\} \] が成り立つ。後者におけるタンジェントの逆関数の値は \(0\) から \(\frac{1}{2}\pi\) とする。 [置換 \(t = \dfrac{x - x_{0}}{y + y_{0}}\) を使うと積分が \(\displaystyle 2\int_{0}^{X} \frac{dt}{1 - at^{2}}\) の形に簡略化される]
-
\(\displaystyle \int_{0}^{a} \frac{dx}{x + \sqrt{a^{2} - x^{2}}} = \dfrac{1}{4}\pi\) を示せ。
(Math. Trip. 1913.)
-
\(a \gt 1\) なら \(\displaystyle \int_{-1}^{1} \frac{\sqrt{1 - x^{2}}}{a - x}\, dx = \pi\{a - \sqrt{a^{2} - 1}\}\) だと示せ。
-
\(p \gt 1\) かつ \(0 \lt q \lt 1\) なら \[ \int_{0}^{1} \frac{dx}{\sqrt{\{1 + (p^{2} - 1)x\}\{1 - (1 - q^{2}) x\}}} = \frac{2\omega}{(p + q)\sin\omega} \] だと示せ。\(\omega\) はコサインが \(\dfrac{1 + pq}{p + q}\) の正の鋭角とする。
-
\(a \gt b \gt 0\) なら \(\displaystyle \int_{0}^{2\pi} \frac{\sin^{2}\theta\, d\theta}{a - b\cos\theta} = \frac{2\pi}{b^{2}} \{a - \sqrt{a^{2} - b^{2}}\}\) が成り立つ。
(Math. Trip. 1904.)
-
\(a \gt \sqrt{b^{2} + c^{2}}\) なら \[ \int_{0}^{\pi} \frac{d\theta}{a + b\cos\theta + c\sin\theta} = \frac{2}{\sqrt{a^{2} - b^{2} - c^{2}}} \arctan \left\{\frac{\sqrt{a^{2} - b^{2} - c^{2}}}{c}\right\} \] だと示せ。タンジェントの逆関数の値は \(0\) から \(\pi\) とする。
-
\(f(x)\) が連続で負の値を取らないとする。\(\displaystyle\int_{a}^{b} f(x)\, dx = 0\) なら、\(a\) と \(b\) の間の全ての \(x\) に対して \(f(x) = 0\) だと示せ。 [\(f(x)\) が \(x = \xi\) で正の実数 \(k\) に等しいとすると、\(f(x)\) の連続性より区間 \([\xi - \delta, \xi + \delta]\) であって区間全体で \(f(x) \gt \frac{1}{2}k\) が成り立つものが存在する。このとき積分の値は \(\delta k\) より大きくなる]
-
積分に対するシュワルツの不等式: 次を示せ: \[ \left(\int_{a}^{b} \phi\psi\, dx\right)^{2} \leq \int_{a}^{b} \phi^{2}\, dx \int_{a}^{b} \psi^{2}\, dx \]
[§156–§157 の定義および不等式 \[ \left(\sum\phi_{\nu}\psi_{\nu}\, \delta_{\nu}\right)^{2} \leq \sum\phi_{\nu}^{2}\, \delta_{\nu} \sum\psi_{\nu}^{2}\, \delta_{\nu} \] を使う。参考: 第一章に関するその他の例 10]
-
\(P_{n}\) を \[ P_{n}(x) = \frac{1}{(\beta - \alpha)^{n} n!} \left(\frac{d}{dx}\right)^{n} \{(x - \alpha)(\beta - x)\}^{n} \] と定めると、\(P_{n}(x)\) は次数 \(n\) の多項式となる。さらに \(P_{n}\) には次数が \(n\) 未満の任意の多項式 \(\theta(x)\) に対して \[ \int_{\alpha}^{\beta} P_{n}(x)\theta(x)\, dx = 0 \] が成り立つという性質がある。 [\(\theta(x)\) の次数を \(m\) として、部分積分を \(m + 1\) 回行う。さらに \(\theta^{(m+1)}(x) = 0\) を使う]
-
\(m \neq n\) なら \(\displaystyle \int_{\alpha}^{\beta} P_{m}(x) P_{n}(x)\, dx = 0\) だが、\(m = n\) ならこの積分の値は \(\dfrac{\beta - \alpha}{2n + 1}\) だと示せ。
-
次数が \(n\) より小さい任意の多項式 \(\theta(x)\) に対して次の等式が成り立つ \(n\) 次の方程式を \(Q_{n}(x)\) とする: \[ \int_{\alpha}^{\beta} Q_{n}(x)\theta(x)\, dx = 0 \] \(Q_{n}(x)\) が \(P_{n}(x)\) の定数倍だと示せ。
[\(Q_{n} - \kappa P_{n}\) の次数が \(n - 1\) となるように \(\kappa\) を選べる。このとき \[ \int_{\alpha}^{\beta} Q_{n}(Q_{n} - \kappa P_{n})\, dx = 0,\quad \int_{\alpha}^{\beta} P_{n}(Q_{n} - \kappa P_{n})\, dx = 0 \] であり、ここから \[ \int_{\alpha}^{\beta} (Q_{n} - \kappa P_{n})^{2}\, dx = 0 \] が成り立つと分かる。この等式には問題 41 を適用できる]
-
定積分の近似: 積分 \(\displaystyle\int_{a}^{b} \phi(x)\, dx\) の値を \(\dfrac{1}{2}(b - a) \{\phi(a) + \phi(b)\}\) と近似したときの誤差が \(\dfrac{1}{12}M(b - a)^{3}\) より小さいと示せ。\(M\) は区間 \([a, b]\) における \(|\phi''(x)|\) の最大値とする。また \((b - a)\phi\{\dfrac{1}{2}(a + b)\}\) と近似したときの誤差は \(\dfrac{1}{24}M(b - a)^{3}\) より小さいと示せ。 [\(f'(x) = \phi(x)\) として問題 4, 5 を適用する] さらに積分を \[ \dfrac{1}{6}(b - a)\left[\phi(a) + \phi(b) + 4\phi\{\dfrac{1}{2}(a + b)\}\right] \] と近似したときの誤差が \(\dfrac{1}{2880}M(b - a)^{5}\) より小さいと示せ。ここでは \(M\) を \(\phi^{(4)}(x)\) の最大値とする。 [問題 6 を使う。非常に正確な近似を与えるこの公式はシンプソン則 (Simpson's Rule) と呼ばれる。これは一つ目の近似の三分の一と二つ目の近似の三分の二の和となっている]
シンプソン則が計算する近似値が、曲線 \(y = \phi(x)\) 上の \(x\) 座標が \(a,\ \dfrac{1}{2}(a + b),\ b\) である三点を通る軸が \(y\) 軸に平行な放物線と三つの直線 \(x = a,\ x = b,\ y = 0\) で囲まれた部分の面積だと示せ。
\(\phi(x)\) が三次方程式なら \(\phi^{(4)(x)} = 0\) なので、シンプソン則は正確な等式となることが分かる。つまり \(x\) 座標が \(a,\ \dfrac{1}{2}(a + b),\ b\) の三点が与えられたとき、それらを通る曲線 \(y = \alpha + \beta x + \gamma x^{2} + \delta x^{3}\) が無限に存在するが、その全てが同じ面積を与える。そして \(\delta = 0\) である曲線が一つ存在し、これが放物線である。
-
\(\phi(x)\) が五次の多項式なら、\(x^{2} - x + \dfrac{1}{10} = 0\) の根を \(\alpha\) と \(\beta\) として \[ \int_{0}^{1} \phi(x)\, dx = \dfrac{1}{18}\{5\phi(\alpha) + 8\phi(\tfrac{1}{2}) + 5\phi(\beta)\} \] が成り立つ。
(Math. Trip. 1909.)
-
シンプソン則を \(\displaystyle\dfrac{1}{4}\pi = \int_{0}^{1} \frac{dx}{1 + x^{2}}\) に適用し、\(\pi\) を計算せよ。 [積分は \(.7833\ldots\) となる。積分を \(0\) から \(\dfrac{1}{2}\) と \(\dfrac{1}{2}\) から \(1\) に分割してからシンプソン則を使うと \(.7853916\ldots\) を得る。正確な値は \(.7853981\ldots\) である]
-
次を示せ: \[ 8.9 \lt \int_{3}^{5} \sqrt{4 + x^{2}}\, dx \lt 9 \]
(Math. Trip. 1903.)
-
次の積分を小数点以下第二位まで計算せよ: \[ \int_{0}^{1} \frac{dx}{1 + x},\quad \int_{0}^{1} \frac{dx}{\sqrt{1 + x^{4}}},\quad \int_{0}^{\pi} \sqrt{\sin x}\, dx,\quad \int_{0}^{\pi} \frac{\sin x}{x}\, dx \] [最後の積分の被積分関数は \(x = 0\) で定義されないが、\(x = 0\) で \(1\) と定めれば積分区間で連続となる]
-
実は \(f^{(n)}(0)\) の存在だけを仮定すれば十分である。R. H. Fowler, "The elementary differential geometry of plane curves" (Cambridge Tracts in Mathematics, No. 20, p. 104) を参照[return]
-
訳注: 楕円上の二点で引いた接線が直行するとき、中心とそれらの点を結んだ二つの半径を共役 (conjugate) であると言う。[return]
-
複数の変数を考えるときに注意を要する点は二つの変数を考えれば十分説明できる。これから述べる定理はどれも三つ以上の変数へ簡単に一般化できる。[return]
-
もちろん \(\Delta x = \delta x\) が成り立つのはそうなるように \(\Delta r = PP_{2}\) を選んだからに過ぎない。他のどんな値を選んだとしても、\(\Delta x\) と \(\Delta r\) はここで使ったものに比例する値となる。[return]
-
\(|\delta x| + |\delta y|\) や \(\sqrt{\delta x^{2} + \delta y^{2}}\) でも構わない。[return]
-
ここからの議論はグルサ著 Cours d'Analyse (second edition), vol. i, pp. 171 et seq. から取った。ただこの文献では本書よりもずっと一般的にこの問題を扱っている。[return]
-
この \(s\) と \(S\) は一般に同じ分割に対応しない。[return]
-
ここからの等式に登場する関数はもちろん連続とする。定積分は連続関数に対してしか定義されない。[return]
-
問題 9–13 はギブソン教授による Elementary Treatise on the Calculus から取った。[return]
-
この例と次の例では全ての導関数の連続性を仮定する。[return]
-
問題 33–35, 38, 40 に関連する話題については Messenger of Mathematics, vol. xxxv のブロムウィッチ博士による論文を参照。[return]