第八章 無限数列と無限積分の収束
§165 級数の表記
第四章で無限級数の収束・発散・振動の意味を説明した。そのとき定義を確認するために示した例は幾何級数 \[ 1 + x + x^{2} + \cdots \] から派生した級数およびこれに近い級数が中心だった。本章ではこの話題をさらに体系的に掘り下げ、解析学で最もよく登場する種類の級数の収束を判定するのに利用できる定理を証明する。
これからは \[ u_{m} + u_{m+1} + \cdots + u_{n} = \sum_{m}^{n} \phi(\nu) \] と表記し、無限級数 \(u_{0} + u_{1} + u_{2} + \cdots\) を \(\sum\limits_{0}^{\infty} u_{n}\) あるいは単に \(\sum u_{n}\) と書く1。
§166 正項級数
級数の項が全て正の実数だと仮定すると収束の議論が比較的簡単になる2。まずはこの条件を満たす級数を考えるが、その理由は扱いが簡単なためだけではなく、負あるいは複素数の項を含む級数の収束の議論が正の項だけからなる級数の収束の議論に帰着できる場合が多いためでもある。
級数の収束と発散を議論するときには、有限個の項を無視しても構わない。そのため級数に含まれる負あるいは複素数の項が有限個なら、そういった項を除いた残りの部分にこれから説明する正項級数に対する定理を適用できる。
§167 正項級数の収束判定法
§77 で証明した重要な定理をここに繰り返しておいた方がいいだろう。
正項級数は収束するか \(\infty\) に発散するかのどちらかで、振動することはない。
\(\sum u_{n}\) が収束するための必要十分条件は、ある \(K\) が存在して全ての \(n\) で \[ u_{0} + u_{1} + \cdots + u_{n} \lt K \] となることである。
全ての \(n\) に対して \(v_{n} \leq u_{n}\) が成り立ち \(\sum u_{n}\) が収束するなら、\(\sum v_{n}\) は収束して \(\sum v_{n} \leq \sum u_{n}\) が成り立つ。より一般的には、定数 \(K\) に対して \(v_{n} \leq Ku_{n}\) なら \(\sum v_{n}\) は収束して \(\sum v_{n} \leq K \sum u_{n}\) が成り立つ。また \(\sum u_{n}\) が発散して \(v_{n} \geq Ku_{n}\) なら \(\sum v_{n}\) は発散する3。
こういった判定法を使って \(\sum v_{n}\) が発散や収束を調べるときには、十分大きな \(n\) に対してだけ条件が満たされれば十分である。つまりとある有限の値 \(n_{0}\) より大きい \(n\) で満たされればよい。ただしもちろんこの場合は結論の \(\sum v_{n} \leq K \sum u_{n}\) が成り立つとは限らない。
この定理の特に重要な場合を次に示す:
\(\sum u_{n}\) が収束 (発散) して \(u_{n}/v_{n}\) が \(n \to \infty\) で \(0\) でない極限に向かうなら、\(\sum v_{n}\) は収束 (発散) する。
§168 コーシーの判定法とダランベールの判定法
現在の私たちが知っている特別なクラスの級数の収束に関する重要な事実の一つに、\(\sum r^{n}\) は \(r \lt 1\) なら収束し \(r \geq 1\) なら発散するというものがある4。前節の定理 C を \(u_{n} = r^{n}\) に適用するのが自然であり、次の結果が直ちに得られる:
\(r \lt 1\) に対して十分大きな \(n\) で \(v_{n} \leq Kr^{n}\) なら \(\sum v_{n}\) は収束する。
\(K = 1\) とすれば、この条件は \(v_{n}^{1/n} \leq r\) となる。ここから正項級数の収束に関するコーシーの判定法 (Cauchy's test) として知られる命題を得る:
\(r \lt 1\) に対して十分大きな \(n\) で \(v_{n}^{1/n} \leq r\) なら \(\sum v_{n}\) は収束する。
発散についても対応する判定法がある:
無限個の \(n\) で \(v_{n}^{1/n} \geq 1\) なら \(\sum v_{n}\) は発散する。
\(v_{n}^{1/n} \geq 1\) なら \(v_{n} \geq 1\) なので、証明はほとんど必要ない。結果 2 と結果 2a は非常に広い応用を持つが、次の異なる判定法の方が使いやすい場合もある:
\(r \lt 1\) に対して十分大きな全ての \(n\) で \(\dfrac{v_{n+1}}{v_{n}} \leq r\) なら級数 \(\sum v_{n}\) は収束する。
証明には \(n \geq n_{0}\) で \(\dfrac{v_{n+1}}{v_{n}} \leq r\) のとき \[ v_{n} = \frac{v_{n}}{v_{n-1}}\, \frac{v_{n-1}}{v_{n-2}} \cdots \frac{v_{n_{0}+1}}{v_{n_{0}}}\, v_{n_{0}} \leq \frac{v_{n_{0}}}{r^{n_{0}}} r^{n} \] という事実を利用する。収束する級数 \(\sum r^{n}\) と比較すれば結果が得られる。この判定法は ダランベールの判定法 (d'Alembert's test) として知られる。後で見るように、ダランベールの判定法はコーシーの判定法よりも理論的に一般性が劣る。つまりダランベールの判定法が使えるならコーシーの判定法が必ず使えるが、逆は成り立たないことがある。さらにダランベールの判定法から得られる発散の判定法は結果 2a よりずっと一般性が劣る。全ての \(n\) または十分大きな全ての \(n\) で \(v_{n+1}/v_{n} \geq r \geq 1\) なら \(\sum v_{n}\) が発散することは示せるが、無限個の \(n\) で \(v_{n+1}/v_{n} \geq r \geq 1\) なだけでは級数が発散するとは言えない。これに対して結果 2a では条件が無限個の \(n\) で満たされるだけで発散することが分かる。それでもなおダランベールの判定法は実際の問題に対して非常に有用となる。\(v_{n}\) が複雑な関数のときには \(v_{n+1}/v_{n}\) を考えた方がずっと簡単な場合が多いためである。
解析学で登場する非常に単純なケースでは、\(n \to \infty\) で \(v_{n+1}/v_{n}\) や \(v_{n}^{1/n}\) が極限に向かう。この極限が \(1\) より小さいなら上述の結果 2 あるいは結果 3 の条件が満たされるので、次の結果が得られる:
\(n \to \infty\) で \(v_{n}^{1/n}\) または \(\dfrac{v_{n+1}}{v_{n}}\) が \(1\) より小さい極限に向かうなら、級数 \(\sum v_{n}\) は収束する。
二つの関数が \(1\) より大きい極限に収束するなら \(\sum v_{n}\) が発散することはほとんど明らかに分かる。細かな証明は読者への練習問題とする。\(v_{n}^{1/n}\) または \(v_{n+1}/v_{n}\) が \(1\) に収束するときにはこの判定法が使えなくなる。また \(v_{n}^{1/n}\) あるいは \(v_{n+1}/v_{n}\) が常に \(1\) より小さいものの、\(1\) に限りなく近づく値を取りながら振動する場合さえ判定できない。さらに \(v_{n+1}/v_{n}\) があるときには \(1\) より小さくあるときには \(1\) より大きい値を取って振動する場合にも判定できない。\(v_{n}^{1/n}\) がこのように振動する場合には結果 2a から級数の発散が示せるが、これ以外の多くの場合ではより細かな判定法が必要となる。
-
コーシーとダランベールの判定法 (上述の結果 4) を級数 \(\sum n^{k} r^{n}\) に適用せよ。\(k\) は正の有理数とする。
[\(v_{n+1}/v_{n} = \{(n + 1)/n\}^{k} r \to r\) なので、ダランベールの判定法から \(r \lt 1\) のとき収束し \(r \gt 1\) のとき発散すると分かる。\(r = 1\) のときはこの判定法が適用できないが、級数は明らかに発散する。\(\lim n^{1/n} = 1\) (例 27.11) だから、コーシーの判定法を使っても同じ結論が直ちに得られる]
-
級数 \(\sum(An^{k} + Bn^{k-1} + \cdots + K) r^{n}\) を考えよ。 [\(A\) を正とする。\(r^{n}\) の係数を \(P(n)\) とすれば \(P(n)/n^{k} \to A\) となる。§167 の定理 D から、この級数は \(\sum n^{k} r^{n}\) と同じように振る舞うと分かる]
-
次の級数を考えよ: \[ \sum \frac{An^{k} + Bn^{k-1} + \cdots + K} {\alpha n^{l} + \beta n^{l-1} + \cdots + \kappa} r^{n}\quad (A \gt 0,\ \alpha \gt 0) \]
[この級数は \(\sum n^{k-l} r^{n}\) と同じように振る舞う。\(r = 1\) かつ \(k \lt l\) の場合にはさらに議論が必要になる]
-
第四章のその他の例 17 では、級数 \[ \sum \frac{1}{n(n + 1)},\quad \sum \frac{1}{n(n + 1) \cdots (n + p)} \] が収束することを見た。コーシーの判定法とアダマールの判定法ではこの級数の振る舞いを判定できないことを示せ。 [\(\lim u_{n}^{1/n} = \lim (u_{n+1}/u_{n}) = 1\) から分かる]
-
\(2\) 以上の整数 \(p\) に対する \(\sum n^{-p}\) が収束することを示せ。[\(\lim \{n(n + 1)\cdots (n + p - 1)\}/n^{p} = 1\) だから、問題 4 の級数の収束性から従う。§77 の \(\text{(7)}\) では \(p = 1\) のとき発散することを見た。\(p \leq 0\) なら明らかに発散する]
-
級数 \[ \sum \frac{An^{k} + Bn^{k-1} + \cdots + K} {\alpha n^{l} + \beta n^{l-1} + \cdots + \kappa} \] が \(l \gt k + 1\) なら収束し、\(l \leq k + 1\) なら発散することを示せ。
-
\(m_{n}\) が正の整数で \(m_{n+1} \gt m_{n}\) とする。\(\sum r^{m_{n}}\) は \(r \lt 1\) なら収束し、\(r \geq 1\) なら発散する。例えば級数 \(1 + r + r^{4} + r^{9} + \cdots\) は \(r \lt 1\) なら収束し、\(r \geq 1\) なら発散する。
-
\(r = .1\) に対する級数 \(1 + 2r + 2r^{4} + \cdots\) を小数点以下第二十四位まで計算せよ。\(r = .9\) として同じ級数を小数点以下二位まで計算せよ。 [\(r = .1\) なら最初の \(5\) 項までの和が \(1.2002000020000002\) となり、誤差は \[ 2r^{25} + 2r^{36} + \cdots \lt 2r^{25} + 2r^{36} + 2r^{47} + \cdots = \frac{2r^{25}}{1 - r^{11}} \lt \frac{3}{10^{25}} \] となる。\(r = .9\) なら最初の \(8\) 項の和が \(5.458\ldots\) であり、誤差は \(2r^{64}/(1 - r^{17}) \lt .003\) より小さくなる]
-
\(0 \lt a \lt b \lt 1\) なら \(a + b + a^{2} + b^{2} + a^{3} + \cdots\) は収束する。コーシーの判定法はこの級数に適用できるが、アダマールの判定法は適用できないことを示せ。 [等式 \[ v_{2n+1}/v_{2n} = (b/a)^{n+1} \to \infty,\quad v_{2n+2}/v_{2n+1} = b(a/b)^{n+2} \to 0 \] から分かる]
-
級数 \(1 + r + \dfrac{r^{2}}{2!} + \dfrac{r^{3}}{3!} + \cdots\) と \(1 + r + \dfrac{r^{2}}{2^{2}} + \dfrac{r^{3}}{3^{3}} + \cdots\) は全ての正の \(r\) に対して収束する。
-
\(\sum u_{n}\) が収束するなら \(\sum u_{n}^{2}\) と \(\sum \dfrac{u_{n}}{1 + u_{n}}\) も収束する。
-
\(\sum u_{n}^{2}\) が収束するなら \(\sum \dfrac{u_{n}}{n}\) も収束する。 [不等式 \(\dfrac{2u_{n}}{n} \leq u_{n}^{2} + \dfrac{1}{n^{2}}\) と \(\sum \dfrac{1}{n^{2}}\) が収束する事実から分かる]
-
等式 \[ 1 + \frac{1}{3^{2}} + \frac{1}{5^{2}} + \cdots = \frac{3}{4}\left(1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \cdots \right) \] および \[ 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{5^{2}} + \frac{1}{6^{2}} + \frac{1}{7^{2}} + \frac{1}{9^{2}} + \cdots = \frac{15}{16} \left(1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \cdots\right) \] を示せ。
[一つ目の結果を示すには \[ \begin{aligned} 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \cdots & = \left(1 + \frac{1}{2^{2}}\right) + \left(\frac{1}{3^{2}} + \frac{1}{4^{2}}\right) + \cdots\\ & = 1 + \frac{1}{3^{2}} + \frac{1}{5^{2}} + \cdots + \frac{1}{2^{2}} \left(1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \cdots\right) \end{aligned} \] を使う。この等式は §77 の \(\text{(8)}\) と \(\text{(6)}\) から分かる]
-
\(\sum \dfrac{1}{n}\) が発散することを背理法で示せ。 [この級数が収束するなら、問題 13 と同じ議論で \[ 1 + \dfrac{1}{2} + \dfrac{1}{3} + \cdots = (1 + \dfrac{1}{3} + \dfrac{1}{5} + \cdots) + \dfrac{1}{2} (1 + \dfrac{1}{2} + \dfrac{1}{3}+ \cdots) \] が分かるが、ここからは \[ \dfrac{1}{2} + \dfrac{1}{4} + \dfrac{1}{6} + \cdots = 1 + \dfrac{1}{3} + \dfrac{1}{5} + \cdots \] という式が得られる。左辺の級数の全ての項は右辺の級数の対応する項より小さいので、これはあり得ない]
§169 ディリクレの定理
収束と発散の判定法についてさらに議論を進める前に、正項級数に関する一般的で重要な定理を一つ証明する。
正項級数の和は項の順序を変えても変化しない5。
正項級数 \(u_{0} + u_{1} + u_{2} + \cdots\) が収束するなら、同じ項を並べて変えてできる任意の級数 \[ v_{0} + v_{1} + v_{2} + \cdots \] も収束し、和が元の級数と等しいことをこの定理は意味する。もちろん項を取り除いてはいけない: 全ての \(u\) は \(v\) のどこかで現れ、その逆も成り立つ。
証明は非常に容易である。\(u\) の和を \(s\) とする。\(u\) から任意の数の項を取ってくると、それらの和は \(s\) 以下となる。一方で全ての \(v\) は \(u\) だから、\(v\) から任意の数の項を取ってきてもその和は \(s\) 以下となる。よって \(\sum v_{n}\) は収束し、その和 \(t\) は \(s\) 以下と分かる。同様に \(s \leq t\) も示せるから、\(s = t\) が成り立つ。
§170 正項級数の積
ディリクレの定理から次の系が直ちに得られる:
\(u_{0} + u_{1} + u_{2} + \cdots\) と \(v_{0} + v_{1} + v_{2} + \cdots\) が収束する正項級数で和が \(s,\ t\) なら、級数 \[ u_{0} v_{0} + (u_{1} v_{0} + u_{0} v_{1}) + (u_{2} v_{0} + u_{1} v_{1} + u_{0} v_{2}) + \cdots \] は収束し、その和は \(st\) である。
\(u_{m}v_{n}\) の積を全て並べた二次元の無限配列
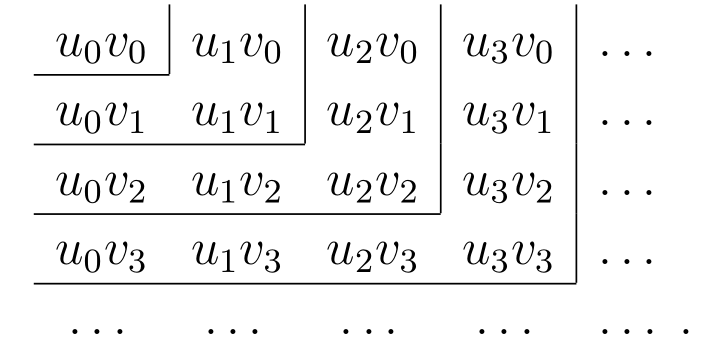
を考える。この配列を並べ替えて得られる通常の無限級数は無数にあるが、それらのうち次の二つに注目する:
-
\(m + n = 0\) となる唯一の項 \(u_{0}v_{0}\) を最初に取り、次に \(m + n = 1\) となる二つの項 \(u_{1}v_{0},\ u_{0}v_{1}\) を取る。次は \(m + n = 2\) となる三つの項 \(u_{2}v_{0},\ u_{1}v_{1},\ u_{0}v_{2}\) と以降同様に取る。こうして得られる級数 \[ u_{0}v_{0} + (u_{1}v_{0} + u_{0}v_{1}) + (u_{2}v_{0} + u_{1}v_{1} + u_{0}v_{2}) + \cdots \] は今考えている級数である。
-
添え字が \(0\) だけからなる \(u_{0}v_{0}\) を最初に取り、次に添え字が \(1\) を含み \(1\) より大きい数字を含まない項 \(u_{1}v_{0},\ u_{1}v_{1},\ u_{0}v_{1}\) を取る。次は添え字が \(2\) を含み \(2\) より大きい数字を含まない項 \(u_{2}v_{0},\ u_{2}v_{1},\ u_{2}v_{2},\ u_{1}v_{2},\ u_{0}v_{2}\) と以降同様に取る。こういったグループの和はそれぞれ \[ \begin{gathered} u_{0}v_{0},\quad (u_{0} + u_{1})(v_{0} + v_{1}) - u_{0}v_{0},\\ (u_{0} + u_{1} + u_{2})(v_{0} + v_{1} + v_{2}) - (u_{0} + u_{1})(v_{0} + v_{1}), \cdots \end{gathered} \] であり、最初の \(n + 1\) グループの和は \[ (u_{0} + u_{1} + \cdots + u_{n})(v_{0} + v_{1} + \cdots + v_{n}) \] となる。よってこの和は \(n \to \infty\) で \(st\) に向かう。なおこうして級数の和を求めると、一つ目・二つ目・三つ目 \(\cdots\) のグループの和は上図の一つ目・二つ目・三つ目 \(\cdots\) の四角形の内側にある項の和に対応する。
このように形成される級数の和は \(st\) である。ここで一つ目の級数は二つ目の級数の順序を入れ替えたものだから、ディリクレの定理より、\(st\) に収束する。よって示すべき事実が証明された。
-
\(r \lt 1\) で次の等式が成り立つことを確認せよ: \[ 1 + r^{2} + r + r^{4} + r^{6} + r^{3} + \cdots = 1 + r + r^{3} + r^{2} + r^{5} + r^{7} + \cdots = \frac{1}{1 - r} \]
-
級数6 \(u_{0} + u_{1} + \cdots\) と \(v_{0} + v_{1} + \cdots\) のどちらかが発散するなら、\(u_{0}v_{0} + (u_{1}v_{0} + u_{0}v_{1}) + (u_{2}v_{0} + u_{1}v_{1} + u_{0}v_{2}) + \cdots\) も発散する。ただし片方の級数が全て \(0\) となる場合は除く。
-
三つの級数 \(u_{0} + u_{1} + \cdots,\ v_{0} + v_{1} + \cdots,\ w_{0} + w_{1} + \cdots\) がそれぞれ \(r,\ s,\ t\) に収束するなら、\(\lambda_{k} = \sum u_{m}v_{n}w_{p}\) としたときの級数 \(\sum \lambda_{k}\) は \(rst\) に収束する。ただし総和は \(m + n + p = k\) となる全ての \(m,\ n,\ p\) に対して取る。
-
\(\sum u_{n}\) と \(\sum v_{n}\) が \(s\) と \(t\) に収束するなら、\(w_{n} = \sum u_{l} v_{m}\) としたときの級数 \(\sum w_{n}\) は \(st\) に収束する。ただし総和は \(lm = n\) となる \(l,\ m\) に対して取る。
§171 収束の速さ
ここまでの例から分かるように、§168 の一般的な判定法では扱えない単純で興味深い正項級数が存在する。\(u_{n+1}/u_{n}\) が \(n \to \infty\) で極限に向かう最も単純な種類の級数を考えると、§168 の判定法はこの極限が \(\bm{1}\) のとき一般に適用できない。例えば 例 67.5 では問題に合わせた個別の方法を使う必要があり、幾何級数ではなく 例 67.4 の級数との比較を使った。
§168 では幾何級数との比較を使って様々な判定法を得たが、実は幾何級数はただ収束するだけではなく非常に速く収束し、この速度は収束に必要な速度よりずっと速い。そのため幾何級数との比較から得られる判定法はかなり大雑把であり、それよりもずっと細かな判定法が必要になる場合も多い。
例 27.7 では \(r \lt 1\) なら \(n \to \infty\) で \(n^{k}r^{n} \to 0\) であり、\(k\) の値は問題にならないことを示した。そして 例 67.1 ではさらに級数 \(\sum n^{k}r^{n}\) が収束することを示した。つまり \(r \lt 1\) なら列 \(r,\ r^{2},\ r^{3},\ \ldots,\ r^{n},\ \ldots\) は \(1^{-k},\ 2^{-k},\ 3^{-k},\ \ldots,\ n^{-k},\ \ldots\) よりも速く \(0\) に近づく。\(r\) が小さくて \(k\) が大きい場合にはこれは想像し難い。例えば一般項が \((2/3)^{n}\) および \(n^{-12}\) と表される二つの列 \[ \begin{alignedat}{4} \dfrac{2}{3}, && \quad \dfrac{4}{9}, && \quad \dfrac{8}{27}, &\quad \cdots; \\ 1, && \quad \dfrac{1}{4096}, && \quad \dfrac{1}{531441}, &\quad \cdots \end{alignedat} \] を考えると、最初は二つ目の列がずっと速く小さくなっているように見えるが、これは全く正しくない: 十分に列が進めば、一つ目の列がはるかに小さくなる。例えば \[ \begin{aligned} (2/3)^{4} & = 16/81 \lt 1/5,\\ (2/3)^{12} & \lt (1/5)^{3} \lt (1/10)^{2},\\ (2/3)^{1000} & \lt (1/10)^{166} \end{aligned} \] だが \(1000^{-12} = 10^{-36}\) に過ぎず、一つ目の列の第 \(1000\) 項は二つ目の列の第 \(1000\) 項の \(10^{130}\) 分の一より小さい。つまり級数 \(\sum n^{-12}\) は \(\sum n^{-2}\) よりはるかに速く収束するが、\(\sum (2/3)^{n}\) は \(\sum n^{-12}\) よりさらに速く収束する7。
§172 その他の収束判定法
正項級数の収束と発散の判定法をさらに二つ紹介する。それぞれマクローリンの (コーシーの) 積分判定法 (Maclaurin's (Cauchy's) Integral Test) およびコーシーの凝集判定法 (Cauchy's Condensation Test) と呼ばれる。どちらも完全に一般的とはとても言えないが、この章で必要となる程度には一般性を持つ。
二つの判定法を使うにあたって関数 \(u_{n}\) に仮定をもう一つ追加する。これまで \(u_{n}\) は正であること以外の仮定をしてこなかったが、これからは \(\bm{u_{n}}\) は \(\bm{n}\) に関して単調減少だとする。つまり \(u_{n+1} \leq u_{n}\) が全ての \(n\) あるいは十分大きな全ての \(n\) で成り立つとする。
この条件は最も重要なケースの全てで満たされる。というのも前述のディリクレの定理から収束と発散の振る舞いを変えることなく項を並び替えられるので、正項級数を扱う限りこの制限は実質ないようなものだと考えても構わない。級数の項を大きさの降順に並べ替えてしまえば、その降順の級数に判定法を適用できる。
この二つの判定法に進むのに先立って、アーベルの定理と呼ばれる単純で重要な定理8を示す。この定理は発散の判定ができるのに対して収束の判定ができず、この意味で一方向の定理となっている。しかし本質的には上述の二つの定理よりも基礎的な性質を持つ。
§173 アーベルの定理
単調減少の正項級数 \(\sum u_{n}\) が収束するなら \(\lim nu_{n} = 0\) が成り立つ。
\(nu_{n}\) が \(0\) に向かわないとする。このときある \(\delta\) があって、無限に多くの \(n\) で \(nu_{n} \geq \delta\) が成り立つ。この条件を満たす最初の \(n\) を \(n_{1}\) とする。さらにこの条件を満たす \(n\) で \(n_{1}\) の二倍より大きいものを \(n_{2}\) として、\(n_{2}\) の二倍より大きいものを \(n_{3}\) として以下同様に定める。すると \(n_{1},\ n_{2},\ n_{3},\ \ldots\) は \(n_{2} \gt 2n_{1},\ n_{3} \gt 2n_{2},\ \ldots\) を満たす。また \(n_{2} - n_{1} \gt \frac{1}{2}n_{2},\ n_{3} - n_{2} \gt \frac{1}{2}n_{3},\ \ldots\) および \(n_{1}u_{n_{1}} \geq \delta,\ n_{2}u_{n_{2}} \geq \delta,\ \ldots\) も成り立つ。一方 \(n\) が増加すると \(u_{n}\) は減少するので、次が分かる: \[ \begin{gathered} u_{0} + u_{1} + \cdots + u_{n_{1} - 1} \geq n_{1}u_{n_{1}} \geq \delta,\\ u_{n_{1}} + \cdots + u_{n_{2} - 1} \geq (n_{2} - n_{1})u_{n_{2}} \gt \dfrac{1}{2} n_{2}u_{n_{2}} \geq \dfrac{1}{2} \delta,\\ u_{n_{2}} + \cdots + u_{n_{3} - 1} \geq (n_{3} - n_{2})u_{n_{3}} \gt \dfrac{1}{2} n_{3}u_{n_{3}} \geq \dfrac{1}{2} \delta, \end{gathered} \] 以下同様だから、級数 \(\sum u_{n}\) の項を括弧でまとめて得られる級数は次の発散級数よりも真に大きい: \[ \delta + \dfrac{1}{2} \delta + \dfrac{1}{2} \delta + \cdots \] よって \(\sum u_{n}\) は発散する。
-
アーベルの定理を使って \(\sum (1/n)\) と \(\sum \{1/(an + b)\}\) が発散することを示せ。 [\(nu_{n} \to 1\) および \(nu_{n} \to 1/a\) となる]
-
\(n\) が増加すると \(u_{n}\) が減少するという仮定を省くとアーベルの定理が正しくないことを示せ。 [\(n\) が平方数のとき \(u_{n} = 1/n\) でそれ以外のとき \(u_{n} = 1/n^{2}\) となる級数 \[ 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{4} + \frac{1}{5^{2}} + \frac{1}{6^{2}} + \frac{1}{7^{2}} + \frac{1}{8^{2}} + \frac{1}{9} + \frac{1}{10^{2}} + \cdots \] は、次の形に並び替えられる: \[ \frac{1}{2^{2}} + \frac{1}{3^{2}} + \frac{1}{5^{2}} + \frac{1}{6^{2}} + \frac{1}{7^{2}} + \frac{1}{8^{2}} + \frac{1}{10^{2}} + \cdots + \left(1 + \frac{1}{4} + \frac{1}{9} + \cdots\right) \] 並び替えて得られる二つの級数は収束するので、並び替える前の級数も収束する。一方で \(n\) が平方数なら \(nu_{1} = 1\) だから、明らかに \(nu_{n} \to 0\) でない]
-
アーベルの定理の逆は正しくない: 言い換えると、\(n\) が増加するとき \(u_{n}\) が減少して \(\lim nu_{n} = 0\) だとしても、\(\sum u_{n}\) が収束するとは限らない。
[級数 \(\sum(1/n)\) の第一項を \(1\) 倍し、第二項を \(\frac{1}{2}\) 倍し、次の二項を \(\frac{1}{3}\) 倍し、次の四項を \(\frac{1}{4}\) 倍し、次の八項を \(\frac{1}{5}\) 倍し、以下同様とする。新しい級数を括弧でまとめると次を得る: \[ 1 + \dfrac{1}{2} · \dfrac{1}{2} + \dfrac{1}{3} \left(\dfrac{1}{3} + \dfrac{1}{4}\right) + \dfrac{1}{4} \left(\dfrac{1}{5} + \dfrac{1}{6} + \dfrac{1}{7} + \dfrac{1}{8}\right) + \cdots \] この級数は次の発散級数より大きい: \[ 1 + \dfrac{1}{2} · \dfrac{1}{2} + \dfrac{1}{3} · \dfrac{1}{2} + \dfrac{1}{4} · \dfrac{1}{2} + \cdots \] よって発散する。一方で \[ 1 + \dfrac{1}{2} · \dfrac{1}{2} + \dfrac{1}{3} · \dfrac{1}{3} + \dfrac{1}{3} · \dfrac{1}{4} + \dfrac{1}{4} · \dfrac{1}{5} + \dfrac{1}{4} · \dfrac{1}{6} + \cdots \] は \(nu_{n} \to 0\) という条件を満たす。実際 \(2^{\nu-2} \lt n \leq 2^{\nu-1}\) なら \(nu_{n} = 1/\nu\) であり、\(n \to \infty\) で \(\nu \to \infty\) となる]
§174 マクローリン・コーシーの積分判定法
\(n\) が増加するとき \(u_{n}\) が単調に減少するなら、\(u_{n} = \phi(n)\) とみなして \(x = n\) で \(\phi(n)\) という値を取る連続単調減少関数 \(\phi(x)\) が存在すると仮定できる。すると任意の正の整数 \(\nu\) に対して \(\nu - 1 \leq x \leq \nu\) で \[ \phi(\nu - 1) \geq \phi(x) \geq \phi(\nu) \] が成り立つ。 \[ v_{\nu} = \phi(\nu - 1) - \int_{\nu-1}^{\nu} \phi(x)\, dx = \int_{\nu-1}^{\nu} \{\phi(\nu - 1) - \phi(x)\}\, dx \] と定めると \[ 0 \leq v_{\nu} \leq \phi(\nu - 1) - \phi(\nu) \] であり、\(\sum v_{\nu}\) は正項級数となる。さらに \[ v_{2} + v_{3} + \cdots + v_{n} \leq \phi(1) - \phi(n) \leq \phi(1) \] だから、\(\sum v_{\nu}\) は収束する。よって \(v_{2} + v_{3} + \cdots + v_{n}\) つまり \[ \sum_{1}^{n-1} \phi(\nu) - \int_{1}^{n} \phi(x)\, dx \] は \(n \to \infty\) で正の極限に向かう。
\(\Phi(\xi)\) を次のように定義する: \[ \Phi(\xi) = \int_{1}^{\xi} \phi(x)\, dx \] このとき \(\Phi(\xi)\) は \(\xi\) に関して連続で単調増加となり、 \[ u_{1} + u_{2} + \cdots + u_{n-1} - \Phi(n) \] は \(n \to \infty\) で \(\phi(1)\) より小さい正の極限に向かう。よって \(n \to \infty\) で \(\Phi(n)\) が極限に向かうなら \(\sum u_{\nu}\) も極限に向かい、\(\Phi(n)\) が無限大に向かうなら \(\sum u_{\nu}\) も無限大に向かう。また \(\Phi(n)\) は単調増加だから、\(\xi \to \infty\) で極限に向かうか無限大に向かうかのどちらかである。以上より次の結果が得られる:
\(1\) より大きい全ての \(x\) に対して \(\phi(x)\) が連続で常に正であり、\(x\) が増加するとき \(\phi(x)\) が単調減少だとする。このとき級数 \(\phi(1) + \phi(2) + \cdots\) は \[ \Phi(\xi) = \int_{1}^{\xi} \phi(x)\, dx \] が \(\xi \to \infty\) で極限 \(l\) に向かうなら極限に向かい、\(\Phi(\xi)\) が無限大に向かうなら無限大に向かう。極限に向かう場合には、級数の和は \(\phi(1) + l\) 以下となる。
正確に言えば級数の和は \(\phi(1) + l\) より小さくなる。§160 の \(\text{(6)}\) と 第七章のその他の例 41 から \(v_{\nu} \lt \phi(\nu - 1) - \phi(\nu)\) とならないのは \(\phi(x) = \phi(\nu)\) のときだと分かるが、区間 \([\nu - 1, \nu]\) 全体で \(\phi(x) = \phi(\nu)\) が成り立たない限りこうはならない。しかしこの条件が全ての \(\nu\) で成り立つことはあり得ない。
-
\(\displaystyle \sum_{1}^{\infty} \frac{1}{n^{2} + 1} \lt \dfrac{1}{2} + \dfrac{1}{4}\pi\) を示せ。
-
\(\displaystyle -\dfrac{1}{2} \pi \lt \sum_{1}^{\infty} \frac{a}{a^{2} + n^{2}} \lt \dfrac{1}{2} \pi\) を示せ。
(Math. Trip. 1909.)
-
\(m \gt 0\) なら \(\displaystyle \frac{1}{m^{2}} + \frac{1}{(m + 1)^{2}} + \frac{1}{(m + 2)^{2}} + \cdots \lt \frac{m + 1}{m}\) だと示せ。
§175 級数 \(∑ n^{-s}\)
マクローリン (コーシー) の積分判定法の応用で圧倒的に一番重要なのは、次の級数に対する応用である: \[ 1^{-s} + 2^{-s} + 3^{-s} + \cdots + n^{-s} + \cdots \] \(s\) は適当な有理数とする。ここまでに §77 と 例 67.14 と 例 69.1 で \(s = 1\) ならこの級数が発散することを見た。
\(s \leq 0\) なら級数は明らかに発散する。\(s \gt 0\) なら \(n\) の増加と共に \(u_{n}\) は単調減少するので、積分判定法を適用できる。ここでは \(s \neq 1\) で \[ \Phi(\xi) = \int_{1}^{\xi} \frac{dx}{x^{s}} = \frac{\xi^{1-s} - 1}{1 - s} \] が成り立つ。\(s \gt 1\) なら \(\xi \to \infty\) で \(\xi^{1-s} \to 0\) だから \[ \Phi(\xi) \to \frac{1}{(s - 1)} = l \] となる。また \(s \lt 1\) なら \(\xi \to \infty\) で \(\xi^{1-s} \to \infty\) となる。以上の結果を次にまとめる:
級数 \(\sum n^{-s}\) は \(s \gt 1\) なら収束し、\(s \leq 1\) なら発散する。収束するなら和は \(s/(s - 1)\) より小さい。
\(s \lt 1\) でこの級数が発散するという結果は、発散することが分かっている級数 \(\sum (1/n)\) との比較を使っても得られる。
しかしそれでも、積分判定法を \(\sum (1/n)\) に適用すると判定に失敗するのを確認しておこう。 \[ \Phi(\xi) = \int_{1}^{\xi} \frac{dx}{x} \] であり、\(\xi \to \infty\) で \(\Phi(\xi) \to \infty\) となるのは簡単に示せる。\(\xi \gt 2^{n}\) なら \[ \Phi(\xi) \gt \int_{1}^{2^{n}} \frac{dx}{x} = \int_{1}^{2} \frac{dx}{x} + \int_{2}^{4} \frac{dx}{x} + \cdots + \int_{2^{n-1}}^{2^{n}} \frac{dx}{x} \] が成り立つ。\(x = 2^{r}u\) とすれば \[ \int_{2^{r}}^{2^{r+1}} \frac{dx}{x} = \int_{1}^{2} \frac{du}{u} \] だから \(\displaystyle\Phi(\xi) \gt n\int_{1}^{2} \frac{du}{u}\) であり、\(\xi \to \infty\) で \(\Phi(\xi) \to \infty\) となる。
-
上述と同様の議論を使って、\(s \lt 1\) なら\(\displaystyle\Phi(\xi) = \int_{1}^{\xi} \frac{dx}{x^{s}}\) が \(\xi\) と共に無限大に向かうことを積分を使わずに示せ。
-
級数 \(\sum n^{-2},\ \sum n^{-3/2},\ \sum n^{-11/10}\) は収束し、その和はそれぞれ \(2,\ 3,\ 11\) 以下となる。級数 \(\sum n^{-1/2},\ \sum n^{-10/11}\) は発散する。
-
\(a \gt 0\) とする。級数 \(\sum \dfrac{n^{s}}{n^{t} + a}\) は \(t \gt 1 + s\) なら収束し、\(1 \leq 1 + s\) なら発散する。 [\(\sum n^{s-t}\) と比較する]
-
次の級数の収束と発散を議論せよ: \[ \sum\frac{a_{1}n^{s_{1}} + a_{2}n^{s_{2}} + \cdots + a_{k}n^{s_{k}}} {b_{1}n^{t_{1}} + b_{2}n^{t_{2}} + \cdots + b_{l}n^{t_{l}}} \] 記号は全て正で、\(s_{i}\) と \(t_{i}\) は降順に並んだ有理数とする。
-
次を示せ: \[ \begin{gathered} 2\sqrt{n} - 2 \lt \frac{1}{\sqrt{1}} + \frac{1}{\sqrt{2}} + \cdots + \frac{1}{\sqrt{n}} \lt 2\sqrt{n} - 1, \\ \dfrac{1}{2} \pi \lt \frac{1}{2\sqrt{1}} + \frac{1}{3\sqrt{2}} + \frac{1}{4\sqrt{3}} + \cdots \lt \dfrac{1}{2}(\pi + 1) \end{gathered} \]
(Math. Trip. 1911.)
-
\(\phi(n) \to l \gt 1\) なら \(\sum n^{-\phi(n)}\) は収束する。\(\phi(n) \to l \lt 1\) なら \(\sum n^{-\phi(n)}\) は発散する。
§176 コーシーの凝集判定法
§172 で触れた判定法の二つ目を次に示す:
\(u_{n} = \phi(n)\) が \(n\) の単調減少関数なら、\(\sum \phi(n)\) は \(\sum 2^{n}\phi(2^{n})\) と同じように収束または発散する。
証明には §77 で \(\sum(1/n)\) に対して使ったのと同じ議論を使う。まず \[ \begin{aligned} \phi(3) + \phi(4) & \geq 2\phi(4), \\ \phi(5) + \phi(6) + \cdots + \phi(8) & \geq 4\phi(8), \\ \cdots \cdots \cdots \\ \phi(2^{n} + 1) + \phi(2^{n} + 2) + \cdots + \phi(2^{n+1}) & \geq 2^{n}\phi(2^{n+1}) \end{aligned} \] が成り立つ。\(\sum 2^{n}\phi(2^{n})\) が発散するなら \(\sum 2^{n+1}\phi(2^{n+1})\) および \(\sum 2^{n}\phi(2^{n+1})\) も発散するので、これらの不等式から \(\sum\phi(n)\) が発散することが分かる。
一方で \[ \begin{aligned} \phi(2) + \phi(3) & \leq 2\phi(2),\\ \phi(4) + \phi(5) + \cdots + \phi(7) & \leq 4\phi(4),\\ \cdots \cdots \cdots \\ \phi(2^{n} + 1) + \phi(2^{n} + 2) + \cdots + \phi(2^{n+1}) & \leq 2^{n}\phi(2^{n}) \end{aligned} \] からは \(\sum 2^{n}\phi(2^{n})\) が収束するなら \(\sum \phi(n)\) も収束すると分かる。示すべき命題はこれで証明された。
今の私たちにとって、この判定法の応用範囲は積分判定法のそれと大差ない。例えば凝集判定法を使えば級数 \(\sum n^{-s}\) を積分判定法を使った場合と同じぐらい簡単に議論できる。つまり \(\sum n^{-s}\) は \(\sum 2^{n}2^{-ns}\) と同じように収束または発散すると分かるので、ここから \(s \gt 1\) なら収束し \(s \leq 1\) なら発散すると結論できる。
-
\(a\) を \(1\) より大きい正の整数とする。\(\sum \phi(n)\) は \(\sum a^{n}\phi(a^{n})\) と同じように収束または発散すると示せ。 [上と同じ議論を使い、項を \(a,\ a^{2},\ a^{3},\ \ldots\) 個ずつまとめる]
-
\(\sum 2^{n}\phi(2^{n})\) が収束するとき当然 \(\lim 2^{n}\phi(2^{n}) = 0\) が成り立つ。これを使って §173 のアーベルの定理を導け。
§177 無限積分
§174 の積分判定法によると、\(\phi(x)\) が常に正で \(x\) に関して単調減少なら、級数 \(\sum \phi(n)\) の収束と発散は積分関数 \(\Phi(x)\) が \(x \to \infty\) で極限に向かうか無限大に向かうかに一致する。\(\Phi(x)\) が極限に向かうとすると、 \[ \lim_{x \to \infty} \int_{1}^{x} \phi(t)\, dt = l \] が成り立つ。このとき積分 \[ \int_{1}^{\infty} \phi(t)\, dt \] が収束して値 \(l\) を持つと言うことにする。この積分を無限積分 (infinite integral) と呼ぶ。
上述の定義では \(\phi(t)\) が正で単調減少だとしたが、そうでない場合にも自然に定義を拡張できる。さらに積分の下端が \(0\) であるべき特別な理由もない。こうして次の定義が導かれる:
\(\phi(t)\) が \(t > a\) で連続で \[ \lim_{x \to \infty} \int_{a}^{x} \phi(t)\, dt = l \] が成り立つなら、無限積分 \[ \int_{a}^{\infty}\phi(t)\, dt \qquad \text{(1)} \] が収束して値が \(l\) になると言う。
無限積分と区別するために、第七章で定義した下端 \(a\) から上端 \(A\) までの通常の積分を有限積分 (finite integral) と呼ぶことがある。
一方で \[ \int_{a}^{x}\phi(t)\, dt \to \infty \] なら、積分は \(\infty\) に発散すると言う。\(-\infty\) についても同様に定義する。さらに以上のどれでもないなら、\(x \to \infty\) で積分は有限または無限に振動すると言う。
この定義に関して注意すべき点を述べる。
-
\(\Phi(x)\) を \[ \int_{a}^{x}\phi(t)\, dt = \Phi(x) \] と定義すれば、左辺の積分が収束・発散・振動するのは \(\Phi(x)\) が \(x \to \infty\) で極限に向かう・\(\infty\) または \(-\infty\) に向かう・振動するときとなる。\(\Phi(x)\) が極限に向かうときその極限を \(\Phi(\infty)\) と表記すれば、積分の値も \(\Phi(\infty)\) となる。より一般的に言えば、無限積分の値は \(\phi(x)\) の不定積分の一つを \(\Phi(x)\) として \(\Phi(\infty) - \Phi(a)\) と表せる。
-
\(\phi(t)\) が常に正となる特別な場合には \(\Phi(x)\) は \(x\) の単調増加関数となり、積分は収束するかそうでなければ \(\infty\) に発散する。
-
積分 \(\text{(1)}\) の値はもちろん \(a\) によって変化するが、\(t\) の値は関係がない。\(t\) を他の文字と入れ替えても意味は変化しない (参考: §157)。
-
\(2\) や \(\frac{1}{2}\pi\) といった有限の値を持つ式を無限積分と呼ぶのは読者を困惑させるに違いない。無限積分と有限積分の違いは無限級数と有限級数の違いと同じようなものと考えるとよい: 無限級数が必ず発散するなどとは誰も思わない。
-
§156–§157 で積分 \(\displaystyle\int_{a}^{x} \phi(t)\, dt\) は一重の極限、つまりとある有限の和の極限として定義された。そのため無限積分は極限の極限であり、こういった値は反復極限 (repeated limit) と呼ばれる。無限積分は有限積分と本質的に異なる概念であり、だからこそここで個別に定義をした。
-
§174 の積分判定法は次のように言い換えられる: \(\phi(x)\) が常に正で \(x\) に関して単調増加なら、無限級数 \(\sum\phi(n)\) の収束と発散は無限積分 \(\displaystyle\int_{1}^{\infty} \phi(x)\, dx\) の収束と発散に一致する。
-
無限積分に対する §77 の \(\text{(1)}\)–\(\text{(6)}\) と同様の結果の証明に難しい部分はないだろう。例えば \(\text{(2)}\) に対応する命題は次のようになる: \(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) が収束するなら \(b \gt a\) に対する \(\displaystyle\int_{b}^{\infty} \phi(x)\, dx\) も収束し \[ \int_{a}^{\infty} \phi(x)\, dx = \int_{a}^{b} \phi(x)\, dx + \int_{b}^{\infty}\phi(x)\, dx \] が成り立つ。
§178 被積分関数が正の無限積分
§177 の式 \(\text{(1)}\) で定義される無限積分の収束と発散に関して、§167 の定理 A–D と同様の関係を考える。定理 A が級数だけでなく積分でも正しいことは §177 の \(\text{(ii)}\) で見た。また定理 B に対応する命題は「無限積分 \(\text{(1)}\) が収束するための必要十分条件は、\(a\) より大きい全ての \(x\) で \[ \int_{a}^{x} \phi(t)\, dt \lt K \] となるよう \(K\) を取れること」となる。
同様に定理 C には「\(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) が収束し、\(a\) より大きい任意の \(x\) で \(\psi(x) \leq K\phi(x)\) なら、\(\displaystyle\int_{a}^{\infty} \psi(x)\, dx\) も収束して \[ \int_{a}^{\infty} \psi(x)\, dx \leq K\int_{a}^{\infty} \phi(x)\, dx \] が成り立つ」という命題が対応する。発散に対応する判定法の定式化は読者に任せる。
一方で §168 のダランベールの判定法に対応する積分に関する命題は存在しない。これは積分には "連続する項" が存在しないことによる。またコーシーの判定法に対応する命題は存在するが、あまり重要でない上に命題の定式化には関数 \(\phi(x) = r^{x}\) に関する詳細な議論 (第九章で行うもの) が必要になる。最も重要な判定法は次の積分との比較によって得られる: \[ \int_{a}^{\infty} \frac{dx}{x^{s}}\quad (a \gt 0) \] §175 で調べたこの積分の収束と発散についての結果を次にまとめる:
\(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) は \(s \gt 1\) に対して \(x \geq a\) で \(\phi(x) \lt Kx^{-s}\) なら収束し、\(s \leq 1\) に対して \(x \geq a\) で \(\phi(x) \gt Kx^{-s}\) なら発散する。特に \(\lim x^{s}\phi(x) = l\) で \(l \gt 0\) なら、積分は \(s \gt 1\) か \(s \leq 1\) かに応じて収束または発散する。
収束する無限級数の重要な性質の中に、対応する性質が無限積分にないものが一つある: \(\sum \phi(n)\) が収束するなら \(\phi(n) \to 0\) だが、\(\phi(x)\) が常に正で \(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) だとしても \(\phi(x) \to 0\) だとは限らない。
例としてグラフが次の図の細い線で表される関数 \(\phi(x)\) を考える。\(x = 1,\ 2,\ 3\) に対応するピークの高さは \(1\) で、幅は \(x = n\) のとき \(2/(n + 1)^{2}\) とする。ピークの面積は \(1/(n + 1)^{2}\) であり、任意の \(\xi\) に対して \[ \int_{0}^{\xi} \phi(x)\, dx \lt \sum_{0}^{\infty} \frac{1}{(n + 1)^{2}} \] が成り立つ。したがって \(\displaystyle\int_{0}^{\infty} \phi(x)\, dx\) は収束する。しかし \(\phi(x) \to 0\) は成り立たない。
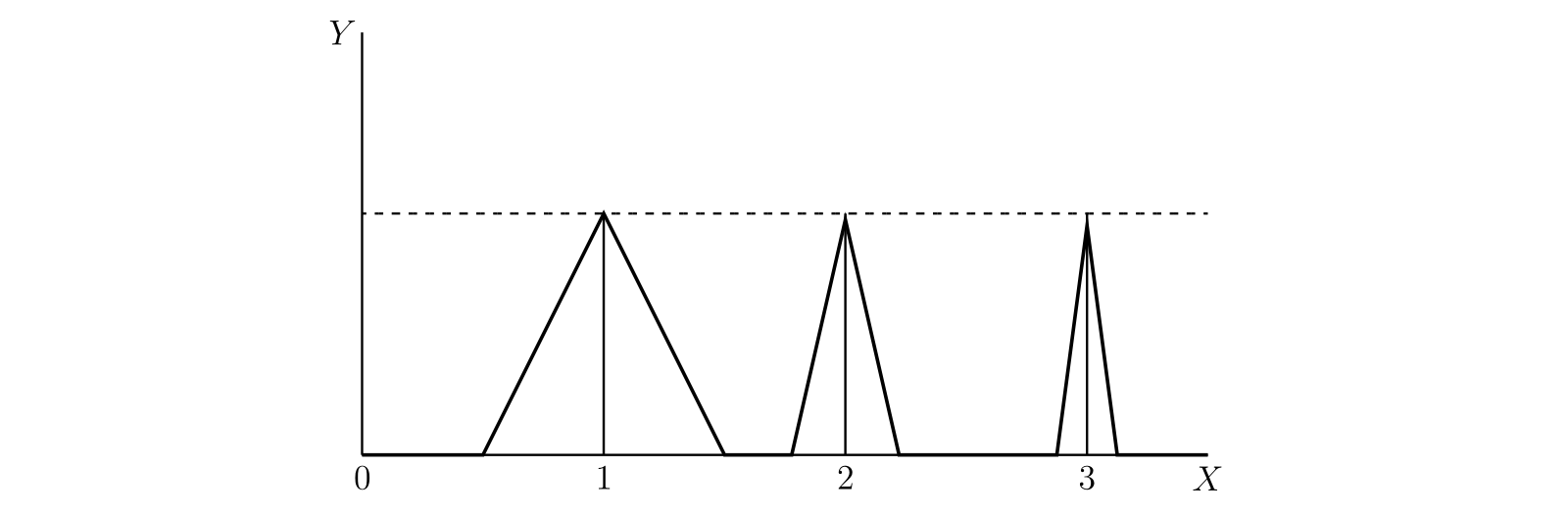
-
積分 \[ \int_{a}^{\infty} \frac{\alpha x^{r} + \beta x^{r-1} + \cdots + \lambda} {Ax^{s} + Bx^{s-1} + \cdots + L}\, dx \] は \(s \gt r + 1\) なら収束し、それ以外のとき発散する。ただし \(\alpha\) と \(A\) は正で、\(a\) は分母の根の最大値より大きいとする。
-
次の積分のうち収束するのはどれか? \[ \displaystyle\int_{a}^{\infty} \frac{dx}{\sqrt{x}},\quad \displaystyle\int_{a}^{\infty} \frac{dx}{x^{4/3}}, \] \[ \int_{a}^{\infty} \frac{dx}{c^{2} + x^{2}},\quad \int_{a}^{\infty} \frac{x\, dx}{c^{2} + x^{2}},\quad \int_{a}^{\infty} \frac{x^{2}\, dx}{c^{2} + x^{2}},\quad \int_{a}^{\infty} \frac{x^{2}\, dx}{\alpha + 2\beta x^{2} + \gamma x^{4}} \] 最初の二つの積分では \(a \gt 0\) で、最後の積分では \(a\) が分母の根の最大値より大きいとする。
-
積分 \[ \int_{a}^{\xi} \cos x\, dx,\quad \int_{a}^{\xi} \sin x\, dx,\quad \int_{a}^{\xi} \cos(\alpha x + \beta)\, dx \] はどれも \(\xi \to \infty\) で有限に振動する。
-
積分 \[ \int_{a}^{\xi} x\cos x\, dx,\quad \int_{a}^{\xi} x^{2}\sin x\, dx\quad \int_{a}^{\xi} x^{n} \cos(\alpha x + \beta)\, dx \] は \(\xi \to \infty\) で無限に振動する。ここで \(n\) は正の整数とする。
-
\(\bm{-\infty}\) への積分: 積分 \(\displaystyle\int_{\xi}^{a} \phi(x)\, dx\) が \(\xi \to -\infty\) で極限 \(l\) に向かうとする。このとき \(\displaystyle\int_{-\infty}^{a} \phi(x)\, dx\) は収束して \(l\) に等しいと言う。この積分は上で議論した無限積分と同様の性質を一つ残らず持つ。定式化は容易だろう。
-
\(\bm{-\infty}\) から \(\bm{+\infty}\) への積分: 積分 \[ \int_{-\infty}^{a} \phi(x)\, dx,\quad \int_{a}^{\infty} \phi(x)\, dx \] がどちらも収束して、その値が \(k,\ l\) だとする。このとき \[ \int_{-\infty}^{\infty} \phi(x)\, dx \] は収束し、その値は \(k + l\) であると言う。
-
次を示せ: \[ \int_{-\infty}^{0} \frac{dx}{1 + x^{2}} = \int_{0}^{\infty} \frac{dx}{1 + x^{2}} = \dfrac{1}{2} \int_{-\infty}^{\infty} \frac{dx}{1 + x^{2}} = \dfrac{1}{2}\pi \]
-
一般に \[ \int_{-\infty}^{\infty} \phi(x^{2})\, dx = 2\int_{0}^{\infty} \phi(x^{2})\, dx \] だと示せ。積分 \(\displaystyle\int_{0}^{\infty} \phi(x^{2})\, dx\) の収束を仮定してよい。
-
\(\displaystyle\int_{0}^{\infty} x\phi(x^{2})\, dx\) が収束するなら \(\displaystyle\int_{-\infty}^{\infty} x\phi(x^{2})\, dx = 0\) だと示せ。
-
§173 で触れたアーベルの定理の拡張: \(\phi(x)\) が常に正で単調減少なら、\(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) が収束するとき \(x\phi(x) \to 0\) が成り立つ。(a) アーベルの定理と積分判定法および (b) §173 と同様の直接的な議論の二つの方法で示せ。
-
\(a = x_{0} \lt x_{1} \lt x_{2} \lt \cdots\) かつ \(x_{n} \to \infty\) として、\(\displaystyle u_{n}= \int_{x_{n}}^{x_{n+1}} \phi(x)\, dx\) と定める。このとき \(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) は \(\sum u_{n}\) と同様に収束または発散する。\(\phi(x)\) が常に正なら逆も正しい。 [逆が一般に正しくないことは \(\phi(x) = \cos x,\ x_{n} = n\pi\) を考えれば分かる]
§179 置換積分と部分積分の無限積分への応用
§161 で議論した定積分の変形公式は無限積分へ拡張できる。
置換積分: 無限積分 \[ \int_{a}^{\infty} \phi(x)\, dx \qquad \text{(1)} \] が収束すると仮定する。さらに \(a\) より大きい任意の \(\xi\) に対して、§161 と同様に \[ \int_{a}^{\xi} \phi(x)\, dx = \int_{b}^{\tau} \phi\{f(t)\}f'(t)\, dt \qquad \text{(2)} \] が成り立ち、\(a = f(b),\ \xi = f(\tau)\) だとする。さらに関係 \(x = f(t)\) が \(x \to \infty\) で \(t \to \infty\) を満たすなら、\(\text{(2)}\) で \(\tau\) (および \(\xi\)) を \(\infty\) に向かせることで積分 \[ \int_{b}^{\infty} \phi\{f(t)\}f'(t)\, dt \qquad \text{(3)} \] が収束し、積分 \(\text{(1)}\) と等しい値を取ると分かる。
一方で \(\tau \to -\infty\) や \(\tau \to c\) で \(\xi \to \infty\) となる可能性もある。前者の場合には \[ \begin{alignedat}{2} \int_{a}^{\infty} \phi(x)\, dx & = & & \lim_{\tau\to-\infty} \int_{b}^{\tau} \phi\{f(t)\}f'(t)\, dt\\ & = -& & \lim_{\tau\to-\infty} \int_{\tau}^{b} \phi\{f(t)\}f'(t)\, dt = -\int_{-\infty}^{b} \phi\{f(t)\}f'(t)\, dt \end{alignedat} \] が成り立ち、後者の場合には \[ \int_{a}^{\infty} \phi(x)\, dx = \lim_{\tau\to c} \int_{b}^{\tau} \phi\{f(t)\}f'(t)\, dt \qquad \text{(4)} \] が成り立つ。この等式は §181 でもう一度考える。
もちろん \[ \int_{-\infty}^{a} \phi(x)\, dx,\quad \int_{-\infty}^{\infty} \phi(x)\, dx \] といった積分にも対応する結果が得られるが、ここに細かく書く意味はない。読者は自分で定式化できるだろう。
-
置換 \(x = t^{\alpha}\) を使って、\(s \gt 1\) かつ \(\alpha \gt 0\) なら \[ \int_{1}^{\infty} x^{-s}\, dx = \alpha\int_{1}^{\infty} t^{\alpha(1-s) - 1}\, dt \] だと示せ。直接求めた積分の値と比較して結果が正しいことを確かめよ。
-
\(\displaystyle\int_{a}^{\infty} \phi(x)\, dx\) が収束するなら、その値は次のどちらかに等しい: \[ \alpha\int_{(a-\beta)/\alpha}^{\infty} \phi(\alpha t + \beta)\, dt,\quad -\alpha\int_{-\infty}^{(a-\beta)/\alpha} \phi(\alpha t + \beta)\, dt \] \(\alpha\) が正なら前者で、負なら後者となる。
-
\(\phi(x)\) は常に正で \(x\) に関して単調減少な関数で、\(\alpha,\ \beta\) は任意の実数とする。級数 \(\sum \phi(n)\) が収束するなら \(\sum \phi(\alpha n + \beta)\) も収束し、この逆も成り立つことを示せ。
[置換 \(x = \alpha t + \beta\) を使えば、二つの積分 \[ \int_{a}^{\infty} \phi(x)\, dx,\quad \int_{(a-\beta)/\alpha}^{\infty} \phi(\alpha t + \beta)\, dt \] の収束または発散が一致すると容易に分かる。それから積分判定法を使う]
-
\(\displaystyle \int_{1}^{\infty} \frac{dx}{(1 + x)\sqrt{x}} = \dfrac{1}{2} \pi\) を示せ。 [\(x = t^{2}\) と置換する]
-
\(\displaystyle \int_{0}^{\infty} \frac{\sqrt{x}}{(1 + x)^{2}}\, dx = \dfrac{1}{2}\pi\) を示せ。 [\(x = t^{2}\) と置換して部分積分を使う]
-
\(x \to \infty\) で \(\phi(x) \to h\) かつ \(x \to -\infty\) で \(\phi(x) \to k\) なら \[ \int_{-\infty}^{\infty} \{\phi(x - a) - \phi(x - b)\}\, dx = -(a - b)(h - k) \] が成り立つ。
[等式 \[ \begin{alignedat}{2} \int_{-\xi'}^{\xi} \{\phi(x - a) - \phi(x - b)\}\, dx & = \int_{-\xi'}^{\xi} \phi(x - a)\, dx & & - \int_{-\xi'}^{\xi} \phi(x - b)\, dx\\ & = \int_{-\xi'-a}^{\xi-a} \phi(t)\, dt & & - \int_{-\xi'-b}^{\xi-b} \phi(t)\, dt\\ & = \int_{-\xi'-a}^{-\xi'-b} \phi(t)\, dt & & - \int_{\xi-a}^{\xi-b} \phi(t)\, dt \end{alignedat} \] から分かる。一つ目の積分は \[ (a - b) k + \int_{-\xi'-a}^{-\xi'-b} \rho\, dt \] という形で表せる。ここで \(\rho\) は \(\xi' \to \infty\) のとき \(\rho \to 0\) を満たす。\([-\xi' - a, -\xi' - b]\) における \(\rho\) の絶対値の最大値を \(\kappa\) とすると最後の積分は \(|a - b| \kappa\) 以下である。よって \[ \int_{-\xi'-a}^{-\xi'-b} \phi(t)\, dt \to (a - b) k \] が成り立つ。二つ目の積分も同様に議論できる]
部分積分: §161 で示した部分積分の公式は \[ \int_{a}^{\xi} f(x)\phi'(x)\, dx = f(\xi)\phi(\xi) - f(a)\phi(a) - \int_{a}^{\xi} f'(x)\phi(x)\, dx \] だった。
\(\xi \to \infty\) のときを考えると、もし上記の式の \(\xi\) が含まれる三つの項のうち二つが収束するなら、残りの一つの項も収束する。ここから次の結果が得られる: \[ \int_{a}^{\infty} f(x)\phi'(x)\, dx = \lim_{\xi\to\infty} f(\xi)\phi(\xi) - f(a)\phi(a) - \int_{a}^{\infty} f'(x)\phi(x)\, dx \] もちろん \(-\infty\) からの積分および \(-\infty\) から \(+\infty\) への積分に関しても同様の結果がある。
-
\(\displaystyle \int_{0}^{\infty} \frac{x}{(1 + x)^{3}}\, dx = \dfrac{1}{2} \int_{0}^{\infty} \frac{dx}{(1 + x)^{2}} = \dfrac{1}{2}\) を示せ。
-
\(\displaystyle\int_{0}^{\infty} \frac{x^{2}}{(1 + x)^{4}}\, dx = \dfrac{2}{3} \int_{0}^{\infty} \frac{x}{(1 + x)^{3}}\, dx = \dfrac{1}{3}\) が成り立つ。
-
\(m\) と \(n\) を正の整数として \[ I_{m, n} = \int_{0}^{\infty} \frac{x^{m}\, dx}{(1 + x)^{m+n}} \] と定める。このとき \[ I_{m, n} = \frac{m}{m + n - 1} I_{m-1, n} \] が成り立つ。これを使って \(I_{m, n} = \dfrac{m!\, (n - 2)!}{(m + n - 1)!}\) を示せ。
-
同様に \[ I_{m, n} = \int_{0}^{\infty} \frac{x^{2m+1}\, dx}{(1 + x^{2})^{m+n}} \] なら \[ I_{m, n} = \frac{m}{m + n - 1} I_{m-1, n},\quad 2I_{m, n} = \frac{m!\, (n - 2)!}{(m + n - 1)!} \] が成り立つ。問題 3 に対して置換 \(x = t^{2}\) を適用することでこの結果を確かめよ。
§180 その他の無限積分
第七章で与えた有限積分 ("通常の" 積分) の定義では、(1) 積分区間が有限なことおよび (2) 被積分関数が連続なことが仮定されていた。
しかし「定積分」の意味はこういった仮定が成り立たない場合にも拡張できる。例えばここまで議論してきた "無限" 積分は積分区間が無限であるという点で第七章の積分と異なっている。次は満たされないのが (1) ではなく (2) の場合を考えて、そのときにも何らかの意味を持つ定義を考えよう。ここではそのような定義を一つだけ与える。\(\phi(x)\) が有限個の点 \(x = \xi_{1},\ \xi_{2},\ \ldots,\) を除いて区間 \([a, A]\) で連続であり、例外的な点では \(x\) をどちら側から近づけても \(\phi(x) \to \infty\) または \(\phi(x) \to -\infty\) だとする。
ここで考える必要があるのは \([a, A]\) に含まれる例外的な点が一つだけの場合だけだと分かる: もし例外的な点が複数あるなら、一つ以下になるように \([a, A]\) を有限個の小区間に分割でき、そして例外的な点が一つ含まれる区間に対する積分が定義されていれば、分割された小区間の積分の和として元々の区間の積分を定義できる。さらに \([a, A]\) が持つ唯一の例外的な点 \(\xi\) が区間の端 \(a,\ A\) のいずれかだとも仮定できる。この場合に対する定義が存在すれば、\(a\) と \(A\) の間に \(\xi\) があるときの \(\displaystyle\int_{a}^{A} \phi(x)\, dx\) を \[ \int_{a}^{\xi} \phi(x)\, dx + \int_{\xi}^{A} \phi(x)\, dx \] と定義できる。以降では \(\xi = a\) とする。こうして導かれる定義をほんの少し変更すれば \(\xi = A\) のときの定義が得られる。
\(\phi(x)\) が \(x = a\) を除いた区間 \([a, A]\) の全ての点で連続で、\(a\) より大きい側から \(x\) が \(a\) に近づくとき \(\phi(x) \to \infty\) だとする。例えば \(s \gt 0\) に対する \[ \phi(x) = (x - a)^{-s} \] はこの条件を満たし、特に \(a = 0\) とすれば \(\phi(x) = x^{-s}\) となる。そこで \(s \gt 0\) に対する \[ \int_{0}^{A} \frac{dx}{x^{s}} \qquad \text{(1)} \] をどう定義すべきか考える。
積分 \(\displaystyle\int_{1/A}^{\infty} y^{s-2}\, dy\) は \(s \lt 1\) なら収束する (§175)。この積分は \(\lim\limits_{\eta\to\infty} \displaystyle\int_{1/A}^{\eta} y^{s-2}\, dy\) を意味するが、\(y = 1/x\) と置換すれば \[ \int_{1/A}^{\eta} y^{s-2}\, dy = \int_{1/\eta}^{A} x^{-s}\, dx \] が得られる。積分 \(\lim\limits_{\eta\to\infty} \displaystyle\int_{1/\eta}^{A} x^{-s}\, dx\) つまりは \[ \lim_{\varepsilon\to +0} \int_{\varepsilon}^{A} x^{-s}\, dx \] は \(s \lt 1\) なら存在するので、積分 \(\text{(1)}\) の値をこの極限として定義するのが自然である。同じ議論により、次の等式を使った \(\displaystyle\int_{a}^{A} (x - a)^{-s}\, dx\) の定義を導ける: \[ \int_{a}^{A} (x - a)^{-s}\, dx = \lim_{\varepsilon\to +0} \int_{a+\varepsilon}^{A} (x - a)^{-s}\, dx \]
以上より一般的な定義が導かれる:
積分 \[ \int_{a+\varepsilon}^{A} \phi(x)\, dx \] が \(\varepsilon \to +0\) で極限 \(l\) を持つなら、積分 \[ \int_{a}^{A} \phi(x)\, dx \] が存在して値 \(l\) を持つと言う。
同様に \(x\) が積分の上端 \(A\) に向かうとき \(\phi(x) \to \infty\) なら、\(\displaystyle\int_{a}^{A} \phi(x)\, dx\) を \[ \lim_{\varepsilon \to +0} \int_{a}^{A-\varepsilon} \phi(x)\, dx \] と定義できる。上述の通り、この定義は \(\phi(x)\) の無限点を有限個だけ含む区間 \([a, A]\) まで拡張できる。
\(x\) が積分区間内のとある値に向かうとき被積分関数が \(\infty\) または \(-\infty\) に向かう積分を第二種無限積分 (infinite integral of the second kind) と呼ぶ。第一種無限積分とは §177 から考えた無限積分を言う。§177 の最後に示した命題のほとんど全ては第一種無限積分だけではなく第二種無限積分に対しても成り立つ。
§181 無限積分の例
§179 の式 \(\text{(4)}\) を変形すると \[ \int_{a}^{\infty} \phi(x)\, dx = \int_{b}^{c} \phi\{f(t)\}f'(t)\, dt \qquad \text{(1)} \] を得る。右辺の積分は区間 \([b, \tau]\) に対する積分の \(\tau \to c\) における極限、つまり第二種無限積分として定義される。もし \(\phi\{f(t)\}f'(t)\) が \(t = c\) を無限点として持つなら、この積分は本当に無限積分となる。例として \(1\ \lt m \lt 2\) に対する \(\phi(x) = (1 + x)^{-m}\) を考えると、\(a = 0\) および \(f(t) = 1/(1 - t)\) とすれば \(b = 0,\ c = 1\) だから、\(\text{(1)}\) は \[ \int_{0}^{\infty} \frac{dx}{(1 + x)^{m}} = \int_{0}^{1} (1 - t)^{m-2}\, dt \qquad \text{(2)} \] となる。右辺の積分は確かに第二種無限積分である。
一方で \(\phi\{f(t)\}f'(t)\) が \(t = c\) で連続になる可能性もある。このとき \[ \int_{b}^{c} \phi\{f(t)\}f'(t)\, dt \] は有限積分であり、 \[ \lim_{\tau \to c} \int_{b}^{\tau} \phi\{f(t)\}f'(t)\, dt = \int_{b}^{c} \phi\{f(t)\}f'(t)\, dt \] が §160 の \(\text{(10)}\) から分かる。つまりこの場合には置換 \(x = f(t)\) が無限積分を有限積分に変形する。先ほどの例で \(m \geq 2\) だとこの状況になる。
-
\(\phi(x)\) が \(x = a\) を除いた点で連続で、\(x \to a\) のとき \(\phi(x) \to \infty\) とする。\(\displaystyle\int_{a}^{A} \phi(x)\, dx\) が収束するための必要十分条件は、任意の正の \(\varepsilon\) に対して \[ \int_{a+\varepsilon}^{A} \phi(x)\, dx \lt K \] を満たす定数 \(K\) が存在することである (参考: §178)。
明らかに、\(a\) と \(A\) の間の点 \(A'\) を選んで \((a, A']\) で \(\phi(x)\) が正であるようにできる。もし \(\phi(x)\) が \([a, A]\) 全体で正なら \(A\) を \(A'\) とする。このとき \[ \int_{a+\varepsilon}^{A} \phi(x)\, dx = \int_{a+\varepsilon}^{A'} \phi(x)\, dx + \int_{A'}^{A} \phi(x)\, dx \] が成り立つ。右辺の最初の積分は \(\varepsilon\) を小さくすると大きくなるので、極限または \(\infty\) に向かう。こうすると上記の結果が分かりやすくなる。
条件が満たされないなら \(\displaystyle\int_{a+\varepsilon}^{A} \phi(x)\, dx \to \infty\) となる。このとき積分 \(\displaystyle\int_{a}^{A} \phi(x)\, dx\) は \(+\infty\) に発散すると言う。\(x \to a + 0\) で \(\phi(x) \to \infty\) なら積分は収束するか \(\infty\) に発散するかのどちらかなのは明らかであり、\(\phi(x) \to -\infty\) でも同様のことが言える。
-
\(s \lt 1\) なら \[ \int_{a}^{A} (x - a)^{-s}\, dx = \frac{(A - a)^{1-s}}{1 - s} \] だと示せ。\(s \geq 1\) なら積分は発散する。
-
\(x \to a + 0\) で \(\phi(x) \to \infty\) とする。\(s \lt 1\) に対して \(\phi(x) \lt K(x - a)^{-s}\) なら \(\displaystyle\int_{a}^{A} \phi(x)\, dx\) は収束し、\(s \geq 1\) に対して \(\phi(x) \gt K(x - a)^{-s}\) なら発散する。 [これは §178 で述べた一般的な比較定理に対応する命題を特殊化したものに過ぎない]
-
積分 \[ \begin{gathered} \int_{a}^{A} \frac{dx}{\sqrt{(x - a)(A - x)}},\quad \int_{a}^{A} \frac{dx}{(A - x)\sqrt[3]{x - a}},\quad \int_{a}^{A} \frac{dx}{(A - x)\sqrt[3]{A - x}},\\ \int_{a}^{A} \frac{dx}{\sqrt{x^{2} - a^{2}}},\quad \int_{a}^{A} \frac{dx}{\sqrt[3]{A^{3} - x^{3}}},\quad \int_{a}^{A} \frac{dx}{x^{2} - a^{2}},\quad \int_{a}^{A} \frac{dx}{A^{3} - x^{3}} \end{gathered} \] は収束するか、それとも発散するか?
-
積分 \(\displaystyle \int_{-1}^{1}\frac{dx}{\sqrt[3]{x}},\quad \int_{a-1}^{a+1} \frac{dx}{\sqrt[3]{x - a}}\) は収束し、その値は \(0\) である。
-
積分 \(\displaystyle \int_{0}^{\pi} \frac{dx}{\sqrt{\sin x}}\) は収束する。 [被積分関数は \(x\) が上端および下端に向かうとき \(\infty\) に向かう]
-
積分 \(\displaystyle \int_{0}^{\pi} \frac{dx}{(\sin x)^{s}} \) は \(s \lt 1\) のときに限って収束する。
-
\(t \lt s + 1\) なら積分 \(\displaystyle \int_{0}^{\frac{1}{2}\pi} \frac{x^{s}}{(\sin x)^{t}}\, dx \) は収束する。
-
\(h \gt 0\) に対する \(\displaystyle \int_{0}^{h} \frac{\sin x}{x^{p}}\, dx\) は \(p \lt 2\) なら収束することを示せ。さらに \(0 \lt p \lt 2\) なら \(\displaystyle \int_{0}^{\pi} \frac{\sin x}{x^{p}} dx,\ \) \(\displaystyle \int_{\pi}^{2\pi} \frac{\sin x}{x^{p}}\, dx,\ \) \(\displaystyle \int_{2\pi}^{3\pi} \frac{\sin x}{x^{p}}\, dx,\ \ldots\) は符号を反転させながら絶対値が減少する列となることを示せ。 [\([k\pi, (k + 1)\pi]\) に対する積分を置換 \(x = k\pi + y\) で変形する]
-
\(0 \lt p \lt 2\) に対する積分 \[ \int_{0}^{h} \frac{\sin x}{x^{p}}\, dx \] が \(h = \pi\) で最大値を取ることを示せ。
(Math. Trip. 1911.)
-
積分 \(\displaystyle \int_{0}^{\frac{1}{2} \pi}(\cos x)^{l}(\sin x)^{m}\, dx\) は \(l \gt -1\) かつ \(m \gt -1\) のときに限って収束する。
-
\(s \lt 1\) に対する \[ \int_{0}^{\infty} \frac{x^{s-1}\, dx}{1 + x} \] のような積分は、これまでの定義のどれにも当てはまらない。積分区間が無限でかつ被積分関数が \(x \to +0\) で \(\infty\) となるためである。この積分の自然な定義は \[ \int_{0}^{1} \frac{x^{s-1}\, dx}{1 + x} + \int_{1}^{\infty} \frac{x^{s-1}\, dx}{1 + x} \] となる。ただし二つの積分の収束を仮定する。
一つ目の積分は \(0 \lt s \lt 1\) で収束する第二種無限積分で、二つ目の積分は \(s \lt 1\) で収束する第一種無限積分である。\(s \gt 1\) なら一つ目の積分は通常の有限積分となるが、二つ目の積分が発散する。よって \(0\) から \(\infty\) までの積分が収束するのは \(0 \lt s \lt 1\) のときに限る。
-
\(\displaystyle \int_{0}^{\infty} \frac{x^{s-1}}{1 + x^{t}}\, dx\) が収束するのは \(0 \lt s \lt t\) のときに限ると示せ。
-
積分 \(\displaystyle \int_{0}^{\infty} \frac{x^{s-1} - x^{t-1}}{1 - x}\, dx\) は \(0 \lt s \lt 1\) かつ \(0 \lt t \lt 1\) のときに限って収束する。 [被積分関数は \(x = 1\) で定義されないが、\(x \to 1\) のとき \(x\) がどちらの側から \(1\) に近づいても \((x^{s-1} - x^{t-1})/(1 - x) \to t - s\) が成り立つ。つまり \(x = 1\) の値を \(t - s\) とすれば被積分関数は連続となる。
被積分関数が積分区間内の特定の点で定義されず不連続となるものの、その点で上手く値を定めれば不連続性を取り除ける場合がある。このときには被積分関数の定義がそうなっていると仮定することが多い。例えば積分 \[ \int_{0}^{\frac{1}{2} \pi} \frac{\sin mx}{x}\, dx,\quad \int_{0}^{\frac{1}{2} \pi} \frac{\sin mx}{\sin x}\, dx \] は、\(x = 0\) で被積分関数が \(m\) という値を取るとすれば通常の有限積分となる]
-
置換積分と部分積分: 置換積分と部分積分の公式が第一種だけではなく第二種の無限積分にも拡張できるのは明らかである。§179 と同じように一般的な定理を自分で書いてみるとよい。
-
部分積分を使って、\(s \gt 0,\ t \gt 1\) なら \[ \int_{0}^{1} x^{s-1}(1 - x)^{t-1}\, dx = \frac{t - 1}{s} \int_{0}^{1} x^{s} (1 - x)^{t-2}\, dx \] だと示せ。
-
\(s \gt 0\) なら \(\displaystyle \int_{0}^{1} \frac{x^{s-1}\, dx}{1 + x} = \int_{1}^{\infty} \frac{t^{-s}\, dt}{1 + t}\) が成り立つ。 [\(x = \dfrac{1}{t}\) と置換する]
-
\(0 \lt s \lt 1\) なら \(\displaystyle \int_{0}^{1} \frac{x^{s-1} + x^{-s}}{1 + x}\, dx = \int_{0}^{\infty} \frac{t^{-s}\, dt}{1 + t} = \int_{0}^{\infty} \frac{t^{s-1}\, dt}{1 + t}\) が成り立つ。
-
\(a + b \gt 0\) なら \(\displaystyle \int_{b}^{\infty} \frac{dx}{(x + a)\sqrt{x - b}} = \frac{\pi}{\sqrt{a + b}}\) が成り立つ。
(Math. Trip. 1909.)
-
置換 \(x = \dfrac{t}{1 - t}\) を使って、\(l\) と \(m\) がどちらも正なら \[ \int_{0}^{\infty} \frac{x^{l-1}}{(1 + x)^{l+m}}\, dx = \int_{0}^{1} t^{l-1} (1 - t)^{m-1}\, dt \] だと示せ。
-
置換 \(x = \dfrac{pt}{p + 1 - t}\) を使って、\(l,\ m,\ p\) が全て正なら \[ \int_{0}^{1} x^{l-1} (1 - x)^{m-1}\, \frac{dx}{(x + p)^{l + m}} = \frac{1}{(1 + p)^{l} p^{m}} \int_{0}^{1} t^{l-1} (1 - t)^{m-1}\, dt \] だと示せ。
-
等式 \(\displaystyle \int_{a}^{b} \frac{dx}{\sqrt{(x - a)(b - x)}} = \pi\) および \(\displaystyle \int_{a}^{b} \frac{x\, dx}{\sqrt{(x - a)(b - x)}} = \dfrac{1}{2} \pi (a + b)\) を、(i) \(x = a + (b - a)t^{2},\ \) (ii) \(\dfrac{b - x}{x - a} = t,\ \) (iii) \(x = a\cos^{2} t + b\sin^{2} t\) という三つの置換を使ってそれぞれ示せ。
-
\(s \gt -1\) なら \[ \int_{0}^{\frac{1}{2} \pi} (\sin\theta)^{s}\, d\theta = \int_{0}^{1} \frac{x^{s}\, dx}{\sqrt{1 - x^{2}}} = \dfrac{1}{2} \int_{0}^{1} \frac{x^{\frac{1}{2}(s-1)}\, dx}{\sqrt{1 - x}} = \dfrac{1}{2} \int_{0}^{1} (1 - x)^{\frac{1}{2}(s-1)} \frac{dx}{\sqrt{x}} \] が成り立つ。
-
等式 \[ \begin{aligned} & \int_{0}^{1} \frac{f(x)\, dx}{\sqrt{1 - x^{2}}} = \int_{0}^{\frac{1}{2}\pi} f(\sin\theta)\, d\theta,\\ & \int_{a}^{b} \frac{f(x)\, dx}{\sqrt{(x - a)(b - x)}} = 2\int_{0}^{\frac{1}{2}\pi} f(a\cos^{2}\theta + b\sin^{2}\theta)\, d\theta,\\ & \int_{-a}^{a} f\left\{\sqrt{\frac{a - x}{a + x}}\right\} dx = 4a\int_{0}^{\frac{1}{2}\pi} f(\tan\theta) \cos\theta \sin\theta\, d\theta \end{aligned} \] を示せ。
-
次を示せ: \[ \int_{0}^{1} \frac{dx}{(1 + x)(2 + x) \sqrt{x(1 - x)}} = \pi\left(\frac{1}{\sqrt{2}} - \frac{1}{\sqrt{6}}\right) \]
§182 置換積分の注意点
置換を使った積分の変形で注意が必要な点がいくつかある。例を使ってこれを説明する。
\(J\) を \[ J = \int_{1}^{7} (x^{2} - 6x + 13)\, dx \] とすれば、\(J = 48\) は直接計算できる。置換 \[ y = x^{2} - 6x + 13 \] を考えると \(x = 3 ± \sqrt{y - 4}\) であり、\(x = 1\) で \(y = 8\) および \(x = 7\) で \(y = 20\) となる。ここから \[ J = \int_{8}^{20} y\frac{dx}{dy}\, dy = ±\dfrac{1}{2}\int_{8}^{20} \frac{y\, dy}{\sqrt{y - 4}} \] が得られるように思える。すると不定積分 \[ \dfrac{1}{3}(y - 4)^{3/2} + 4(y - 4)^{1/2} \] から積分が \(±\dfrac{80}{3}\) と計算されるが、どちらの符号を選ぼうとこれは間違っている。
この原因は \(x\) と \(y\) の関係を詳しく見ると明らかになる。関数 \(x^{2} - 6x + 13\) は \(x = 3\) で最小値 \(y = 4\) を持つ。\(x\) が \(1\) から \(3\) に増加するとき \(y\) は \(8\) から \(4\) に減少する。そのため \(dx/dy\) は負で \[ \frac{dx}{dy} = -\frac{1}{2\sqrt{y - 4}} \] が成り立つ。\(x\) が \(3\) から \(7\) に増加するとき \(y\) は \(4\) から \(20\) に増加するので、もう一方の符号を選ぶ必要がある。よって \[ J = \int_{1}^{7} y\, dx = \int_{8}^{4} \left\{-\frac{y}{2\sqrt{y - 4}}\right\} dy + \int_{4}^{20} \frac{y}{2\sqrt{y - 4}}\, dy \] が得られ、この等式を使えば正しい結果が計算できる。
同様に積分 \(\displaystyle\int_{0}^{\pi} dx = \pi\) を置換 \(x = \arcsin y\) で変形するときには、\(0 \leq x \lt \frac{1}{2}\pi\) と \(\frac{1}{2}\pi \lt x \leq \pi\) で \(dx/dy = 1/\sqrt{1 - y^{2}}\) と \(dx/dy = -1/\sqrt{1 - y^{2}}\) が切り替わる点に注意が必要となる。
置換 \(4x^{2} - x + \frac{1}{16} = y\) および \(x = \arcsin y\) を使って、積分 \[ \int_{0}^{1} (4x^{2} - x + \dfrac{1}{16})\, dx,\quad \int_{0}^{\pi} \cos^{2}x\, dx \] を変形せよ。
§183 項に正負が混じる級数
無限級数と第一種および第二種の無限積分は、級数の項や被積分関数の値が正でも負でも定義される。しかし本章で示した収束と発散の特別な判定法とそれを説明するための例では、値が正である場合だけを考えてきた。もちろん項や関数が常に負なら本質な違いはなく、\(u_{n}\) を \(-u_{n}\) に、\(\phi(x)\) を \(-\phi(x)\) に変えれば正の場合に帰着できる。
これまで級数を考えるときには、\(u_{n}\) に対する条件は有限個の項に対して成り立たなくてもよいと明示的にあるいは暗に仮定してきた。つまり条件 (例えば「全ての項が正」) は有限個の項よりも後ろの全ての項で成り立てば十分だった。同様に積分では条件がある定数より後ろの全ての \(\bm{x}\) で満たされる、あるいは \(a\) の近くで被積分関数が無限大に向かうなら有限区間 \((a, a + \delta)\) 内の全ての \(x\) で満たされることが仮定された。そのため例えば \[ \sum \frac{n^{2} - 10}{n^{4}} \] に対しては、\(n \geq 4\) で \(n^{2} - 10 \gt 0\) だから、前に触れた判定法を適用できる。同様に積分 \[ \int_{1}^{\infty} \frac{3x - 7}{(x + 1)^{3}}\, dx,\quad \int_{0}^{1} \frac{1 - 2x}{\sqrt{x}}\, dx \] に対しても、\(x \gt \frac{7}{3}\) なら \(3x - 7 \gt 0\) および \(0 \lt x \lt \frac{1}{2}\) なら \(1 - 2x \gt 0\) だから、正の関数に対する判定法を適用できる。
しかし \(u_{n}\) の値が級数全体で変化する、つまり負の項と正の項がどちらも無限に存在するなら、話は違ってくる。例えば級数 \(1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots\) や、 \[ \int_{1}^{\infty} \frac{\sin x}{x^{s}}\, dx \] のような \(x \to \infty\) で無限に符号が変わる関数の積分、あるいは被積分関数の不連続点 \(a\) に \(x\) を近づけると符号が無限に変わる \[ \int_{a}^{A} \sin\left(\frac{1}{x - a}\right) \frac{dx}{x - a} \] のような積分では、発散と収束に関する議論がより難しくなる。この場合には収束と発散に加えて振動の可能性も考慮しなければならない。
本書ではこういった積分に関するより一般的な問題を考えることはしない。ただ次章では、正の項と負の項をどちらも無限に含むとある簡単な級数を考える必要が生じる。
§184 級数の絶対収束
任意の項が正でも負でもあり得る級数 \(\sum u_{n}\) を考える。 \[ |u_{n}| = \alpha_{n} \] とすると、\(u_{n}\) が正なら \(\alpha_{n} = u_{n}\) で \(u_{n}\) が負なら \(\alpha_{n} = -u_{n}\) となる。さらに新しい数列 \(v_{n}, w_{n}\) を、\(u_{n}\) が正なら \(v_{n} = u_{n},\ w_{n} = 0\) で、\(u_{n}\) が負なら \(v_{n} = 0,\ w_{n} = -u_{n}\) と定義する。同じことを言い換えると、\(u_{n}\) の正負に応じて \(v_{n}\) と \(w_{n}\) のどちらかが \(\alpha_{n}\) と等しくなり、もう一方が \(0\) となる。\(v_{n}\) と \(w_{n}\) は常に正であり、 \[ u_{n} = v_{n} - w_{n},\quad \alpha_{n} = v_{n} + w_{n} \] を満たす。
例えば級数 \(1 - (1/2)^{2} + (1/3)^{2} - \cdots\) を考えているなら \(u_{n} = (-1)^{n-1}/n^{2}\) および \(\alpha_{n} = 1/n^{2}\) であり、\(n\) の偶奇に応じて \(v_{n} = 0\) または \(v_{n} = 1/n^{2}\) および \(w_{n} = 1/n^{2}\) または \(w_{n} = 0\) となる。
こうすると二つのケースを分けて議論できる:
A: \(\sum \alpha_{n}\) が収束すると仮定する。例えば上述の例では \(\sum \alpha_{n}\) つまり \[ 1 + \frac{1}{2^{2}} + \frac{1}{3^{2}} + \cdots \] が収束するのでこのケースとなる。このとき \(\sum v_{n}\) と \(\sum w_{n}\) も収束する: 収束する正項級数の項を取ってできる級数は収束することは 例 30.18 で見た。よって §77 の定理 \(\text{(6)}\) から \(\sum(v_{n} - w_{n})\) つまり \(u_{n}\) も収束し、その値は \(\sum v_{n} - \sum w_{n}\) に等しいと分かる。
ここから次の定義が導かれる:
\(\sum \alpha_{n}\) つまり \(\sum |u_{n}|\) が収束するなら、級数 \(\sum u_{n}\) は絶対収束する (converge absolutely) と言う。
この定義を使えば、先ほど示した命題は「絶対収束する級数 \(\sum u_{n}\) は収束する」となる。さらに正の項と負の項を集めてできる級数も収束し、\(\sum u_{n}\) はその二つの級数の和に等しい。
「絶対収束する級数は収束する」という命題はトートロジーではないか、などと思わないようよく注意しなければならない。\(\sum u_{n}\) が "絶対収束" すると言ったとしても、それは \(\sum u_{n}\) が収束することを直接は意味しない。こう言ったとき私たちが主張しているのは \(\sum |u_{n}|\) という全く別の級数の収束であり、\(\sum u_{n}\) が振動する可能性は決して除かれていない。
-
§84 の "収束の一般原則" を使って絶対収束する級数が収束することを示せ。 [級数 \(\sum |u_{n}|\) が収束するので、与えられた任意の正の \(\varepsilon\) に対して、\(n_{2} \gt n_{1} \geq n_{0}\) で \[ |u_{n_{1}+1}| + |u_{n_{1}+2}| + \cdots + |u_{n_{2}}| \lt \varepsilon \] が成り立つような \(n_{0}\) が存在する。したがって \[ |u_{n_{1}+1} + u_{n_{1}+2} + \cdots + u_{n_{2}}| \lt \varepsilon \] であり、\(\sum u_{n}\) は収束する]
-
\(\sum a_{n}\) を収束する正項級数とする。\(|b_{n}|\leq Ka_{n}\) なら \(\sum b_{n}\) は絶対収束する。
-
\(\sum a_{n}\) を収束する正項級数とする。\(-1 \leq x \leq 1\) に対して級数 \(\sum a_{n}x^{n}\) は絶対収束する。
-
\(\sum a_{n}\) を収束する正項級数とする。\(\sum a_{n} \cos n\theta\) と \(\sum a_{n}\sin n\theta\) は \(\theta\) の値に関わらず絶対収束する。 [§88 で触れた級数 \(\sum r^{n}\cos n\theta\) と \(\sum r^{n}\sin n\theta\) がこの例となる]
-
絶対収束する級数の一部を取ってできる任意の級数は絶対収束する。 [新しい級数の絶対値の級数は、元の級数の絶対値の級数の一部を取ってできる級数となる]
-
\(\sum |u_{n}|\) が収束するなら \[ \left|\sum u_{n} \right| \leq \sum |u_{n}| \] であり、等号の成立は全ての項が同じ符号を持つ場合に限ると示せ。
§185 絶対収束する級数に対するディリクレの定理
§169 のディリクレの定理によると、正項級数の項を並べ替えても和は変わらない。絶対収束する級数もこの性質を持つことは簡単に示せる。\(\sum u_{n}\) を並び替えた級数を \(\sum u'_{n}\) として、\(u_{n}\) から \(\alpha_{n},\ v_{n},\ w_{n}\) を作ったように \(u'_{n}\) から \(\alpha'_{n},\ v'_{n},\ w'_{n}\) を作る。すると \(\sum \alpha'_{n}\) は \(\sum \alpha_{n}\) を並べ替えた級数なので収束し、\(\sum v'_{n}\) と \(\sum w'_{n}\) もそれぞれ \(\sum v_{n}\) と \(\sum w_{n}\) を並べ替えた級数だから収束する。さらにディリクレの定理から \(\sum v'_{n} = \sum v_{n}\) と \(\sum w'_{n} = \sum w_{n}\) が分かる。したがって \[ \sum u'_{n} = \sum v'_{n} - \sum w'_{n} = \sum v_{n} - \sum w_{n} = \sum u_{n} \] が成り立つ。
§186 級数の条件収束
B: 次に二つ目の場合、つまり絶対値の級数 \(\sum \alpha_{n}\) が発散する場合を考える。
\(\sum u_{n}\) が収束して \(\sum |u_{n}|\) が発散するなら、級数 \(\sum u_{n}\) は条件収束する (converge conditionally) と言う。
\(\sum u_{n}\) が条件収束なら、§184 の \(\sum v_{n}\) と \(\sum w_{n}\) は両方とも \(\infty\) に発散する。もし両方とも収束するなら \(\sum(v_{n} + w_{n})\) つまり \(\sum \alpha_{n}\) が収束してしまう。またどちらか (例えば \(\sum w_{n}\)) が収束してもう一方 (\(\sum v_{n}\)) が発散するなら、 \[ \sum_{0}^{N} u_{n} = \sum_{0}^{N} v_{n} - \sum_{0}^{N} w_{n} \qquad \text{(1)} \] は \(N\) と共に \(\infty\) へ向かうが、これは \(\sum u_{n}\) が収束するという仮定に反する。
よって \(\sum v_{n}\) と \(\sum w_{n}\) はどちらも発散する。\(\text{(1)}\) から分かることとして、条件収束する級数の和は \(n\) と共に \(\infty\) に向かう二つの関数の差の極限となる。また収束する正項級数 (例 30.18) や絶対収束する級数 (例 77.5) とは異なり、条件収束する級数の一部を取ってできる級数が収束するとは限らない。さらに条件収束する級数がディリクレの定理が示す性質を持つことはまずなさそうに見える: §185 の証明は \(\sum v_{n}\) と \(\sum w_{n}\) の収束性を使っており、条件収束する場合には証明が最初から上手く行かない。この予想が確かに正しく、今考えている種類の級数ではこの定理が成り立たないことをこれから示そう。
§187 条件収束する級数に対する判定法
条件収束の判定法が §167 などで見た判定法と同じぐらい簡単で一般的になるとは考えにくい。前節 の \(\text{(1)}\) が表すように正の項と負の項が打ち消し合って収束する級数の収束判定は、正項級数の判定法より難しくなると考えるのが自然である。まず、条件収束する級数には比較判定法が使えない。
\(\sum u_{n}\) の収束性から \(\sum v_{n}\) の収束性を示したいとして、 \[ v_{0} + v_{1} + \cdots + v_{n},\quad u_{0} + u_{1} + \cdots + u_{n} \] を考える。もし任意の添え字 \(i\) に対して \(u_{i}\) と \(v_{i}\) が正で \(v_{i}\) が \(u_{i}\) より小さいなら \[ v_{0} + v_{1} + \cdots + v_{n} \lt u_{0} + \cdots + u_{n} \] が成り立ち、\(\sum v_{n}\) は収束する。そうでなく \(u_{i}\) だけが正で、\(v_{i}\) が \(u_{i}\) の絶対値より小さいなら \[ |v_{0}| + |v_{1}| + \cdots + |v_{n}| \lt u_{0} + \cdots + u_{n} \] であり、\(\sum v_{n}\) は絶対収束する。しかし \(u_{i}\) と \(v_{i}\) の符号に制限がない一般的な場合には \[ |v_{0}| + |v_{1}| + \cdots + |v_{n}| \lt |u_{0}| + \cdots + |u_{n}| \] しか得られない。この不等式からは \(\sum u_{n}\) が絶対収束するなら \(\sum v_{n}\) も絶対収束すると分かるが、もし \(\sum u_{n}\) が条件収束しかしないなら、\(\sum v_{n}\) の収束性については何も分からない。
級数 \(1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots\) が収束することをすぐ後で示す。一方で級数 \(\frac{1}{2} + \frac{1}{3} + \frac{1}{4} + \frac{1}{5} + \cdots\) は、各項の絶対値が収束するこの級数より小さいにもかかわらず、発散する。
以上の議論から、条件収束する級数に対する判定法がこの章の前半部分で見た判定法よりずっと特殊な性質を持つのが全く当然だと分かる。
§188 交代級数
最も簡単で最もよく表れる条件収束級数は、正の項と負の項が交互に並んだ交代級数 (alternating series) である。この種の最も重要な級数の収束は、次の命題を使うと判定できる:
\(n\) の正関数 \(\phi(n)\) が \(n \to \infty\) で単調に \(0\) に向かうとする。このとき級数 \[ \phi(0) - \phi(1) + \phi(2) - \cdots \] は収束し、和は \(\phi(0)\) と \(\phi(0) - \phi(1)\) の間にある。
\(\phi(0),\ \phi(1),\ \ldots\) を \(\phi_{0},\ \phi_{1},\ \ldots\) と書くことにして \[ s_{n} = \phi_{0} - \phi_{1} + \phi_{2} - \cdots + (-1)^{n}\phi_{n} \] と定めると \[ s_{2n+1} - s_{2n-1} = \phi_{2n} - \phi_{2n+1}\geq 0,\quad s_{2n} - s_{2n-2} = -(\phi_{2n-1} - \phi_{2n}) \leq 0 \] が成り立つ。よって \(s_{0},\ s_{2},\ s_{4},\ \ldots,\ s_{2n},\ \ldots\) は減少列であり、極限または \(-\infty\) に向かう。同様に \(s_{1},\ s_{3},\ s_{5},\ \ldots,\ s_{2n+1},\ \ldots\) は増加列であり、極限または \(\infty\) に向かう。一方で \(\lim (s_{2n+1} - s_{2n}) = \lim (-1)^{2n+1} \phi_{2n+1} = 0\) が成り立つから、二つの列の極限は同じでなければならない。つまり \(s_{0},\ s_{1},\ \ldots,\ s_{n},\ \ldots\) は極限に向かう。\(s_{0} = \phi_{0}\) および \(s_{1} = \phi_{0} - \phi_{1}\) だから、この極限は明らかに \(\phi_{0}\) と \(\phi_{0} - \phi_{1}\) の間にある。
-
級数 \[ \begin{gathered} 1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots,\quad 1 - \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{3}} - \frac{1}{\sqrt{4}} + \cdots,\\ \sum \frac{(-1)^{n}}{(n + a)},\quad \sum \frac{(-1)^{n}}{\sqrt{n + a}},\quad \sum \frac{(-1)^{n}}{(\sqrt{n} + \sqrt{a})},\quad \sum \frac{(-1)^{n}}{(\sqrt{n} + \sqrt{a})^{2}} \end{gathered} \] はどれも条件収束する。ここで \(a \gt 0\) とする。
-
\(a \gt 0\) に対する級数 \(\sum(-1)^{n}(n + a)^{-s}\) は \(s \gt 1\) なら絶対収束し、\(0 \lt s \leq 1\) なら条件収束し、\(s \leq 0\) なら振動する。
-
§188 で示した級数の和は常に \(s_{n}\) と \(s_{n+1}\) の間にある。級数全体ではなく最初の \(n\) 項だけを取ったときの和の誤差は第 \(n + 1\) 項の絶対値以下である。
-
級数 \[ \sum \frac{(-1)^{n}}{\sqrt{n} + (-1)^{n}} \] を考える。ただし最初のいくつかの項の定義を複雑にしないために \(n = 2\) から級数を始めるとする。この級数を変形すると \[ \sum \left[\left\{ \frac{(-1)^{n}}{\sqrt{n} + (-1)^{n}} - \frac{(-1)^{n}}{\sqrt{n}}\right\} + \frac{(-1)^{n}}{\sqrt{n}}\right] \] つまり \[ \sum \left\{\frac{(-1)^{n}}{\sqrt{n}} - \frac{1}{n + (-1)^{n}\sqrt{n}}\right\} = \sum (\psi_{n} - \chi_{n}) \] とできる。\(\sum \psi_{n}\) は収束するが、\(\chi_{n}\) は常に正で \(\lim n\chi_{n} = 1\) なので \(\sum \chi_{n}\) は発散する。よって最初の級数は、\(\phi_{2} - \phi_{3} + \phi_{4} - \cdots\) という形をしていて \(\phi_{n} \to 0\) にもかかわらず発散する。この例は「\(\phi_{n}\) が単調に \(0\) へ向かう」という条件が上述の結果に不可欠なことを示している。\(\sqrt{2n + 1} - 1 \lt \sqrt{2n} + 1\) だから、いま考えた級数はこの条件を満たさない。
-
§188 の結果における条件が満たされず、\(\phi_{n}\) が単調に極限 \(l\) へ向かうなら、級数 \(\sum (-1)^{n}\phi_{n}\) は有限に振動する。
-
条件収束の級数を並べ替えると和が変化する: \(s\) を級数 \(1 - \frac{1}{2} + \frac{1}{3} - \frac{1}{4} + \cdots\) の和として、最初の \(2n\) 個の項の和を \(s_{2n}\) とする。このとき \(\lim s_{2n} = s\) が成り立つ。
二つの正の項と一つの負の項を交互に並べた級数 \[ 1 + \dfrac{1}{3} - \dfrac{1}{2} + \dfrac{1}{5} + \dfrac{1}{7} - \dfrac{1}{4} + \cdots \qquad \text{(1)} \] を考える。この級数の最初の \(3n\) 個の項の和を \(t_{3n}\) とすると、 \[ \begin{aligned} t_{3n} & = 1 + \frac{1}{3} + \cdots + \frac{1}{4n-1} - \frac{1}{2} - \frac{1}{4} - \cdots - \frac{1}{2n}\\ & = s_{2n} + \frac{1}{2n + 1} + \frac{1}{2n + 3} + \cdots + \frac{1}{4n - 1} \end{aligned} \] が成り立つ。
ここで \[ \lim \left[\frac{1}{2n + 1} - \frac{1}{2n + 2} + \frac{1}{2n + 3} - \cdots + \frac{1}{4n - 1} - \frac{1}{4n}\right] = 0 \] が成り立つ。括弧に含まれる項の和が明らかに \(n/(2n + 1)(2n + 2)\) より小さいためである。そして §156 と §158 からは \[ \lim \left(\frac{1}{2n + 2} + \frac{1}{2n + 4} + \cdots + \frac{1}{4n}\right) = \dfrac{1}{2} \lim \frac{1}{n} \sum_{r=1}^{n} \frac{1}{1 + (r/n)} = \dfrac{1}{2} \int_{1}^{2} \frac{dx}{x} \] が分かる。よって \[ \lim t_{3n} = s + \dfrac{1}{2} \int_{1}^{2} \frac{dx}{x} \] であり、級数 \(\text{(1)}\) の和は \(s\) でないことが判明する。この二つの級数の値を定義する方法を後で示す: §213 と 第九章に関するその他の例 19 を参照。
実は条件収束する級数を並べ替えると、任意の値に収束する級数および \(\infty\) や \(-\infty\) に発散する級数を作れる。その証明はブロムウィッチ著 Infinite Series, p. 68 に譲る。
-
級数 \[ 1 + \frac{1}{\sqrt{3}} - \frac{1}{\sqrt{2}} + \frac{1}{\sqrt{5}} + \frac{1}{\sqrt{7}} - \frac{1}{\sqrt{4}} + \cdots \] は \(\infty\) に発散する。 [ここでは \(s_{2n} = 1 - \dfrac{1}{\sqrt{2}} + \cdots - \dfrac{1}{\sqrt{2n}}\) とすれば \[ t_{3n} = s_{2n} + \frac{1}{\sqrt{2n + 1}} + \frac{1}{\sqrt{2n + 3}} + \cdots + \frac{1}{\sqrt{4n - 1}} \gt s_{2n} + \frac{n}{\sqrt{4n - 1}} \] が成り立つが、\(s_{2n}\) は \(n \to \infty\) で極限に向かう]
§189 アーベルとディリクレの収束判定法
§188 の判定法を含むより一般的な判定法を次に示す:
ディリクレの判定法: \(\phi(n)\) が §188 と同じ仮定を満たし、\(\sum a_{n}\) が収束するか有限に振動するなら、級数 \[ a_{0}\phi_{0} + a_{1}\phi_{1} + a_{2}\phi_{2} + \cdots \] は収束する。
次の等式は簡単に確認できる: \[ \begin{aligned} a_{0}\phi_{0} + a_{1}\phi_{1} + \cdots + a_{n}\phi_{n} = s_{0}(\phi_{0} - \phi_{1}) &+ s_{1}(\phi_{1} - \phi_{2}) + \cdots \\ \cdots &+ s_{n-1}(\phi_{n-1} - \phi_{n}) + s_{n}\phi_{n} \end{aligned} \] ここで \(s_{n} = a_{0} + a_{1} + \cdots + a_{n}\) である。級数 \((\phi_{0} - \phi_{1}) + (\phi_{1} - \phi_{2}) + \cdots\) を考えると、この級数の第 \(n\) 項までの和は \(\phi_{0} - \phi_{n}\) で仮定より \(\lim \phi_{n} = 0\) なので、この級数は収束する。またこの級数の全ての項は正である。さらに \(\sum a_{n}\) は収束しない場合でも有限に振動しかしないので、全ての \(\nu\) で \(|s_{\nu}| \lt K\) が成り立つ定数 \(K\) を見つけられる。よって級数 \[ \sum s_{\nu}(\phi_{\nu} - \phi_{\nu+1}) \] は絶対収束し、 \[ s_{0}(\phi_{0} - \phi_{1}) + s_{1}(\phi_{1} - \phi_{2}) + \cdots + s_{n-1}(\phi_{n-1} - \phi_{n}) \] は \(n \to \infty\) で極限に向かう。加えて \(\phi_{n}\) したがって \(s_{n}\phi_{n}\) は \(0\) に向かうので、 \[ a_{0}\phi_{0} + a_{1}\phi_{1} + \cdots + a_{n}\phi_{n} \] も極限に向かう。すなわち級数 \(\sum a_{\nu}\phi_{\nu}\) は収束する。
アーベルの判定法: もう一つアーベルの名前が付いた判定法がある。ディリクレの判定法よりは応用範囲が狭いが、便利なこともある。
ディリクレの判定法と同様に \(\phi_{n}\) が常に正で単調減少の関数とする。ただし \(n \to \infty\) における \(\phi_{n}\) の極限は \(0\) でなくてもよい。このため \(\phi_{n}\) に関しては仮定が弱いということになる。ただその代わり、\(\sum a_{n}\) に対しては収束するという強い仮定を置く。このとき次が成り立つ:
\(\phi_{n}\) が単調減少の \(n\) の正関数で \(\sum a_{n}\) が収束するなら、\(\sum a_{n} \phi_{n}\) は収束する。
仮定より \(\phi_{n}\) が \(n \to \infty\) で極限に向かうから、極限を \(l\) とすれば \(\lim (\phi_{n} - l) = 0\) が成り立つ。よってディリクレの判定法より、\(\sum a_{n}(\phi_{n} - l)\) は収束する。これと \(\sum a_{n}\) が収束する仮定から \(\sum a_{n}\phi_{n}\) も収束すると分かる。
この結果は次のようにも表せる:
収束する級数の各項に正の減少列を乗じたものは収束する。
-
ディリクレの判定法とアーベルの判定法は収束の基本原理 (§84) を使っても示せる。例えばアーベルの判定法の条件が成り立つとすると、 \[ \begin{aligned} a_{m}\phi_{m} + a_{m+1}\phi_{m+1} + \cdots & + a_{n}\phi_{n} = s_{m, m}(\phi_{m} - \phi_{m+1}) + s_{m, m+1}(\phi_{m+1} - \phi_{m+2})\\ & \quad + \cdots + s_{m, n-1}(\phi_{n-1} - \phi_{n}) + s_{m, n}\phi_{n} \end{aligned} \qquad \text{(1)} \] となる。ここで \[ s_{m, \nu} = a_{m} + a_{m+1} + \cdots + a_{\nu} \] である。
\(s_{m, m},\ s_{m, m+1},\ \ldots,\ s_{m, n}\) の絶対値の最小値と最大値を \(h,\ H\) とすると、\(\text{(1)}\) の左辺は \(h\phi_{m}\) と \(H\phi_{m}\) の間にある。一方で任意の正の実数 \(\varepsilon\) に対して \(m \geq m_{0}\) で \(|s_{m, \nu}| \lt \varepsilon\) となるように \(m_{0}\) を選ぶことができ、よって \(n \gt m \geq m_{0}\) なら \[ |a_{m}\phi_{m} + a_{m+1}\phi_{m+1} + \cdots + a_{n}\phi_{n}| \lt \varepsilon \phi_{m} \leq \varepsilon \phi_{1} \] が成り立つ。よって \(\sum a_{n}\phi_{n}\) は収束する。
-
級数 \(\sum \cos n\theta\) と \(\sum \sin n\theta\) は \(\theta\) が \(\pi\) の倍数でない限り有限に振動する: 二つの級数の第 \(n\) 項までの和を \(s_{n},\ t_{n}\) として \(z = \operatorname{Cis}\theta\) とすると、\(|z| = 1\) および \(z \neq 1\) が成り立つ。よって \[ |s_{n} + it_{n}| = \left|\frac{1 - z^{n}}{1 - z}\right| \leq \frac{1 + |z^{n}|}{|1 - z|} \leq \frac{2}{|1 - z|} \] であり、\(|s_{n}|\) と \(|t_{n}|\) は \(2/|1 - z|\) 以下となる。二つの級数が収束しないことは第 \(n\) 項が \(0\) に向かわないことから分かる (例 24.7, 8)
\(\theta\) が \(\pi\) の倍数ならサインの級数は \(0\) に収束する。\(\theta\) が \(\pi\) の奇数倍ならコサインの級数は有限に振動し、偶数倍なら発散する。
ディリクレの判定法を使うと「\(\phi_{n}\) が \(n\) の正関数で \(n \to \infty\) のとき単調に \(0\) に向かうなら、級数 \[ \sum \phi_{n} \cos n\theta,\quad \sum \phi_{n} \sin n\theta \] は収束する」ことが分かる。ただし \(\theta\) が \(2\pi\) の倍数のときは例外で、この場合には最初の級数が \(\sum \phi_{n}\) となり、収束しないこともあり得る。また \(\sum \phi_{n}\) が収束するなら二つの級数はどちらも全ての \(\theta\) に対して絶対収束するが、この結果の興味深い点は \(\sum \phi_{n}\) が発散する場合への応用にある: このとき問題 6 で示すように、二つの級数は条件収束するが絶対収束しない。またコサインの級数で \(\theta = \pi\) とすると \(\cos n\pi = (-1)^{n}\) なので、前に示した §188 の結果が得られる。
-
\(s \gt 0\) なら \(\sum n^{-s} \cos n\theta\) と \(\sum n^{-s} \sin n\theta\) は収束する。ただし一つ目の級数で \(0 \lt s \leq 1\) かつ \(\theta\) が \(2\pi\)の倍数である場合は除く。
-
問題 3 の級数は \(s \gt 1\) なら絶対収束し、\(0 \lt s \leq 1\) なら条件収束し、\(s \leq 0\) なら振動する (振動は \(s = 0\) なら無限で、\(s \lt 0\) なら有限となる)。例外的な場合を全て見つけよ。
-
\(\sum a_{n}n^{-s}\) が収束または有限に振動するなら、\(t \gt s\) に対する \(\sum a_{n}n^{-t}\) は収束する。
-
\(n\) の正関数 \(\phi_{n}\) が \(n \to \infty\) で単調に \(0\) に向かい、\(\sum \phi_{n}\) が発散すると仮定する。このとき級数 \(\sum \phi_{n} \cos n\theta\) と \(\sum \phi_{n} \sin n\theta\) は絶対収束しない。ただし \(\theta\) が \(\pi\) の倍数のときのサインの級数は除く。 [例えば \(\sum \phi_{n} |\cos n\theta|\) の収束を仮定すると、\(\cos^{2} n\theta \leq |\cos n\theta|\) より \[ \dfrac{1}{2} \sum \phi_{n} (1 + \cos 2n\theta) \] も収束する。しかしディリクレの判定法より \(\sum \phi_{n} \cos 2n\theta\) は収束し、仮定より \(\sum \phi_{n}\) は発散するのでこれはあり得ない。サインの級数についても、\(\theta\) が \(\pi\) の倍数の場合に注意すれば同様に証明できる]
§190 複素級数
ここまでは全ての項が実数の級数だけを考えてきた。続いて \[ \sum u_{n} = \sum (v_{n} + iw_{n}) \] という形の級数を考える。ここで \(u_{n}\) と \(w_{n}\) は実数とする。もちろんこういった級数を考えても、何か全く新しい概念が必要になるわけではない。例えば級数が収束するための必要十分条件は、二つの級数 \[ \sum v_{n},\quad \sum w_{n} \] が両方とも収束することである。しかし重要な複素級数のクラスが一つあるので、それについては紙面を割いて説明する。§184 な自然な拡張として、次のように定義する:
級数 \(\sum u_{n} = \sum (v_{n} + iw_{n})\) が絶対収束する (converge absolutely) とは、級数 \(\sum v_{n}\) と \(\sum w_{n}\) が両方とも絶対収束することを言う。
\(\sum u_{n}\) が絶対収束するための必要十分条件は、\(\sum |u_{n}| = \sum \sqrt{v_{n}^{2} + w_{n}^{2}}\) が収束することである。
証明は次の通り。\(\sum u_{n}\) が絶対収束するなら \(\sum |v_{n}|\) と \(\sum |w_{n}|\) はどちらも収束し、したがって \(\sum \{|v_{n}| + |w_{n}|\}\) も収束する。よって \[ |u_{n}| = \sqrt{v_{n}^{2} + w_{n}^{2}} \leq |v_{n}| + |w_{n}| \] より \(\sum |u_{n}|\) も収束する。一方で \[ |v_{n}| \leq \sqrt{v_{n}^{2} + w_{n}^{2}},\quad |w_{n}| \leq \sqrt{v_{n}^{2} + w_{n}^{2}} \] だから、\(\sum |u_{n}|\) が収束するなら必ず \(\sum |v_{n}|\) と \(\sum |w_{n}|\) も収束する。
絶対収束する複素級数は収束することは、実部と虚部が別々に収束する事実から容易に分かる。さらにディリクレの定理 (§169) は簡単に複素数へ拡張でき、\(\sum v_{n}\) と \(\sum w_{n}\) という級数を別々に考えれば証明できる。
絶対収束する級数の収束性は収束の基本原則を使って直接示すこともできる (参考: 例 77.1)。これは読者への練習問題とする。
§191 べき級数 (その 1)
初等解析学 (サインとコサインおよび次章で触れる対数関数と指数関数) の理論で最も重要な概念の一つが、\(\sum a_{n}x^{n}\) という形の級数への関数の展開である。この級数を \(x\) の べき級数 (power series) と呼ぶ。これまでに登場したべき級数としてはテイラー級数とマクローリン級数 (§148) があるが、そこで考えたのは実変数 \(x\) のべき級数だった。ここからは複素変数 \(z\) のべき級数の一般的な性質をいくつか紹介する。
べき級数 \(\sum a_{n}z^{n}\) は全ての \(z\) で収束するか、特定の範囲の値で収束するか、\(z = 0\) でだけ収束する。
それぞれの例を示せば十分である。
-
級数 \(\bm{\sum \dfrac{z^{n}}{n!}}\) は全ての \(\bm{z}\) で収束する。\(u_{n} = \dfrac{z^{n}}{n!}\) なら \(n \to \infty\) で \[ \frac{|u_{n+1}|}{|u_{n}|} = \dfrac{|z|}{n + 1} \to 0 \] となり、これは \(z\) の値によらない。よってダランベールの判定法より \(\sum |u_{n}|\) は全ての \(z\) で収束し、級数 \(\sum \dfrac{z^{n}}{n!}\) は全ての \(z\) で絶対収束する。べき級数が収束するなら一般に絶対収束することを後で示す。
-
級数 \(\bm{\sum n!\, z^{n}}\) は \(\bm{z = 0}\) 以外で収束しない。\(u_{n} = n!\, z^{n}\) なら \(|u_{n+1}|/|u_{n}| = (n + 1)|z|\) であり、\(u_{n}\) は \(z = 0\) でない限り \(n\) と共に \(\infty\) に向かう。よって (例 27.1, 2, 5 から) 級数の第 \(n\) 項の大きさは \(n\) と共に \(\infty\) に向かうと分かるので、級数は \(z = 0\) でない限り収束しない。\(z = 0\) のとき収束するのは明らかに分かる。
-
\(\bm{\sum z^{n}}\) は \(\bm{|z| \lt 1}\) なら収束し、\(\bm{|z| \geq 1}\) なら収束しない。これは §88 で示した。
これで三つの可能性が全て示せた。
§192 べき級数 (その 2)
べき級数 \(\sum a_{n}z^{n}\) が特定の \(z\) の値 \(z_{1} = r_{1}(\cos\theta_{1} + i\sin\theta_{1})\) で収束するなら、級数は \(|z| \lt r_{1}\) を満たす全ての \(z\) で絶対収束する。
証明は次の通り。\(\sum a_{n}z_{1}^{n}\) の収束より \(\lim a_{n}z_{1}^{n} = 0\) であり、全ての \(n\) で \(|a_{n}z_{1}^{n}| \lt K\) となる定数 \(K\) が存在する。 一方でもし \(|z| = r \lt r_{1}\) なら \[ |a_{n}z^{n}| = |a_{n}z_{1}^{n}| \left(\frac{r}{r_{1}}\right)^{n} \lt K \left(\frac{r}{r_{1}}\right)^{n} \] だから、示すべき命題は幾何級数 \(\sum (r/r_{1})^{n}\) との比較からすぐに示せる。
この命題を言い換えると「もし級数が \(P\) で収束するなら、その級数は \(\bm{P}\) より原点に近い任意の点で絶対収束する」となる。
\(z = z_{1}\) で級数が有限に振動するときにも同じ結果が得られることを示せ。 [部分和を \(s_{n} = a_{0} + a_{1}z_{1} + \cdots + a_{n}z_{1}^{n}\) とすれば、全ての \(n\) で \(|s_{n}| \lt K\) となる定数 \(K\) を見つけられる。一方 \(|a_{n}z_{1}^{n}| = |s_{n} - s_{n-1}| \leq |s_{n-1}| + |s_{n}| \lt 2K\) だから、議論は前と同じように進む]
§193 べき級数の収束領域 (収束円)
\(z = r\) を正の実軸上の任意の点とする。べき級数が \(z = r\) で収束するなら、その級数は円 \(|z| = r\) 内部の全ての点で絶対収束する。特に \(r\) より小さい全ての実数の \(z\) で収束する。
正の軸軸上の点 \(r\) を次のようにして二つのクラスに分ける。一つのクラスには級数が収束する点を入れ、もう一つには収束しない点を入れる。一つ目のクラスは少なくとも一つの点 \(z = 0\) を含むが、級数が全ての \(z\) で収束することもあるので、二つ目のクラスは存在しない可能性がある。ただここでは二つ目のクラスが存在し、さらに一つ目のクラスには \(z = 0\) 以外の点が含まれると仮定する。すると一つ目のクラスに属する全ての点は二つ目のクラスに含まれる点の左側にある。よって二つのクラスを分ける点が存在し、その点は二つのクラスのどちらかに属する。この点を \(z = R\) とすれば、級数は円 \(\bm{|z| = R}\) 内部の全ての点で絶対収束する。
証明は次の通り。円 \(|z| = R\) と正の実軸の交点を \(A\) とする。円 \(|z| = R\) 内部の任意の点を \(P\) とすると、中心が \(O\) で半径が \(R\) より小さく \(P\) を含む円が描ける。この円と \(OA\) が交わる点を \(Q\) とすると級数は \(Q\) で収束し、結果 B から \(P\) で絶対収束すると分かる。
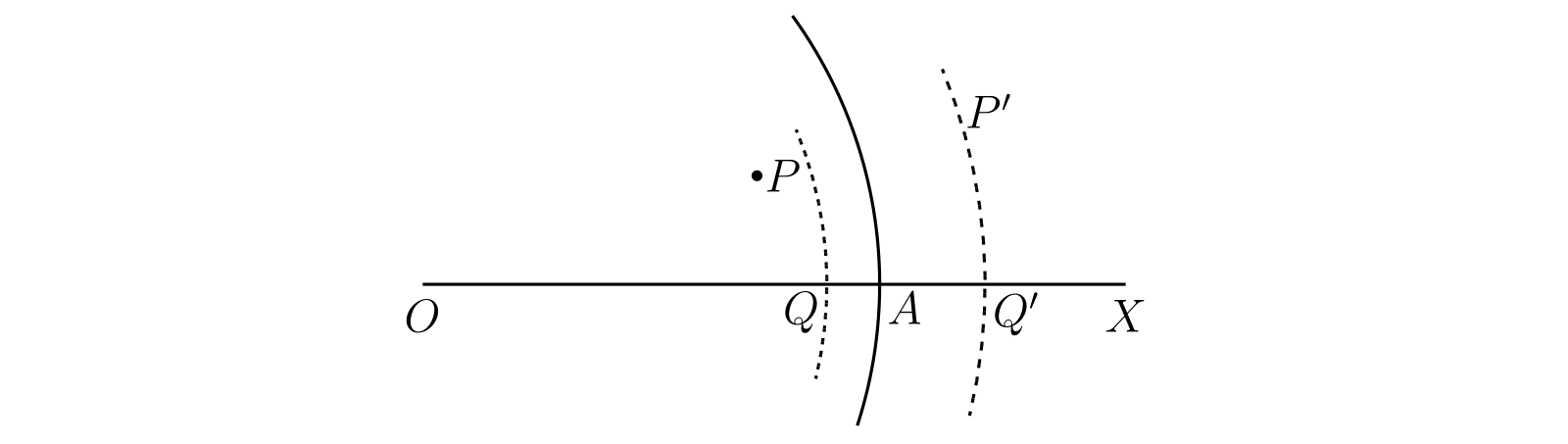
一方で円 \(|z| = R\) の外側にある任意の \(P'\) で級数は収束しない。もし \(P'\) で収束するなら \(P'\) よりも原点に近い全ての点で絶対収束するが、仮定より \(A\) と \(Q'\) の間の点では収束しないのでこれはあり得ない (図 51)。
今までに考えたべき級数の振る舞いには他に二つある: (1) 正の実軸上では \(z = 0\) を除いて任意の点で収束しない (2) 実軸上の全ての点で収束する。容易に分かるように (1) の場合には \(z = 0\) 以外で収束せず、(2) の場合には全ての場所で収束する。以上より次の結果が得られる:
任意のべき級数に対して、次のいずれかが成り立つ:
- \(z = 0\) でのみ収束する。
- 全ての \(z\) で絶対収束する。
- 原点が中心で半径 \(R\) の円の内側にある全ての \(z\) で絶対収束し、その外側にある全ての \(z\) で収束しない。
(3) の円を級数の収束円 (circle of convergence) と呼び、収束円の半径を収束半径 (radius of convergence) と呼ぶ。
ここで注意すべきなのが、この結果からは収束円上の点における級数の振る舞いについては何も分からない点である。次の例で様々な可能性があり得ることを示す。
-
\(a \gt 0\) に対する級数 \(1 + az + a^{2}z^{2} + \cdots\) は \(1/a\) の収束半径を持つ。収束円上では収束せず、\(z = 1/a\) では発散し、収束円上の他の点では有限に振動する。
-
級数 \(\dfrac{z}{1^{2}} + \dfrac{z^{2}}{2^{2}} + \dfrac{z^{3}}{3^{2}} + \cdots\) の収束半径は \(1\) であり、収束円上の全ての点で絶対収束する。
-
より一般に言うと、\(n \to \infty\) で \(|a_{n+1}|/|a_{n}| \to \lambda\) または \(|a_{n}|^{1/n} \to \lambda\) なら、級数 \(a_{0} + a_{1}z + a_{2}z^{2} + \cdots\) の収束半径は \(1/\lambda\) となる。一つ目の場合には \(|z|\) が \(1/\lambda\) より小さいなら \[ \lim \frac{|a_{n+1}z^{n+1}|}{|a_{n}z^{n}|} = \lambda |z| \] が \(1\) より小さくなり、そうでなければ \(1\) よりも大きくなる。後はダランベールの判定法 (§168 の結果 3) を使えば収束が示せる。二つ目の場合にはコーシーの判定法 (§168 の結果 2) を使って同様に議論できる。
-
対数級数: 級数 \[ z - \dfrac{1}{2} z^{2} + \dfrac{1}{3} z^{3} - \cdots \] は "対数" 級数 (logarithmic series) と呼ばれる (こう呼ばれる理由は後述する)。問題 3 を使うとこの級数の収束半径が \(1\) だと分かる。
\(z\) が収束円上にあるときを考える。\(z = \cos\theta + i\sin\theta\) とすれば、対数級数は \[ \cos\theta - \dfrac{1}{2} \cos 2\theta + \dfrac{1}{3} \cos 3\theta - \cdots + i(\sin\theta - \dfrac{1}{2} \sin 2\theta + \dfrac{1}{3} \sin 3\theta - \cdots) \] となる。
よって \(\theta\) が \(\pi\) の奇数倍でないとき実部と虚部は収束するが、絶対収束はしない (例 79.3)。\(\theta\) が \(\pi\) の奇数倍なら \(z = -1\) であり、このときの対数級数 \(-1 - \frac{1}{2} - \frac{1}{3} - \cdots\) は \(-\infty\) に発散する。よって対数級数は収束円上の \(z = -1\) 以外の全ての点で収束すると結論できる。
-
二項級数: 次の級数を考える: \[ 1 + mz + \frac{m(m - 1)}{2!} z^{2} + \frac{m(m - 1)(m - 2)}{3!} z^{3} + \cdots \] \(m\) が正の整数なら、この級数は有限項で打ち切られる。一般には \[ \frac{|a_{n+1}|}{|a_{n}|} = \frac{|m - n|}{n + 1} \to 1 \] なので、収束半径は \(1\) となる。収束円上における収束性は少し難しいのでここでは議論しない9。
§194 べき級数の唯一性
べき級数 \(\sum a_{n} z^{n}\) が \(z = 0\) 以外のとある \(z\) で収束するなら、その和 \(f(z)\) が次の形で表せることは容易に分かる: \[ a_{0} + a_{1}z + a_{2}z^{2} + \cdots + (a_{n} + \varepsilon_{z})z^{n} \] ここで \(\varepsilon_{z}\) は \(|z| \to 0\) のとき \(\varepsilon_{z} \to 0\) を満たす。 証明は次の通り。\(\mu\) を収束半径より小さくかつ \(|z| \lt \mu\) を満たす実数とすれば、\(z\) によらない定数 \(K\) に対して \(|a_{n}| \mu^{n} \lt K\) が成り立つ (参考: §192)。ここから \[ \begin{aligned} \left|f(z) - \sum_{0}^{n} a_{\nu}z^{\nu}\right| & \leq |a_{n+1}| |z^{n+1}| + |a_{n+2}| |z^{n+2}| + \cdots\\ & \lt K \left(\frac{|z|}{\mu}\right)^{n+1} \left(1 + \frac{|z|}{\mu} + \frac{|z|^{2}}{\mu^{2}} + \cdots\right) = \frac{K |z|^{n+1}}{\mu^{n} (\mu - |z|)} \end{aligned} \] が分かる。例 55.15 からは、絶対値がとある実数 \(\mu\) より小さい任意の \(z\) に対して \(\sum a_{n}z^{n} = \sum b_{n}z^{n}\) なら、全ての \(n\) に対して \(a_{n} = b_{n}\) だと分かる。今は詳しく説明できないが、この結果は非常に広く一般化でき、一般化した結果から関数 \(\bm{f(z)}\) はただ一つのべき級数で表されることが分かる。
§195 級数の積
§170 では、二つの正項級数 \(\sum u_{n}\) と \(\sum v_{n}\) が収束するなら次の \(w_{n}\) に対して \(\sum u_{n} × \sum v_{n} = \sum w_{n}\) だと示した: \[ w_{n} = u_{0}v_{n} + u_{1}v_{n-1} + \cdots + u_{n}v_{0} \] この結果は \(\sum u_{n}\) と \(\sum v_{n}\) が絶対収束である場合に拡張できる: 正項級数に対するこの結果の証明はディリクレの定理の簡単な応用であり、絶対収束に対するディリクレの定理は既に証明している。
-
\(|z|\) が級数 \(\sum a_{n}z^{n}\) の収束半径と \(\sum b_{n}z^{n}\) の収束半径の両方より小さいなら、二つの級数の積は \(\sum c_{n}z^{n}\) であり、\(c_{n} = a_{0}b_{n} + a_{1}b_{n-1} + \cdots + a_{n}b_{0}\) となる。
-
\(\sum a_{n}z^{n}\) の収束半径が \(R\) で、\(|z| \lt R\) のときの級数の和が \(f(z)\) で、\(|z|\) が \(R\) と \(1\) の両方より小さいなら、\(f(z)/(1 - z) = \sum s_{n}z^{n}\) が成り立つ。ここで \(s_{n} = a_{0} + a_{1} + \cdots + a_{n}\) とする。
-
\(1/(1 - z)\) の級数を二乗し、\(|z| \lt 1\) なら \(1/(1 - z)^{2} = 1 + 2z + 3z^{2} + \cdots\) だと示せ。
-
同様に \(1/(1 - z)^{3} = 1 + 3z + 6z^{2} + \cdots\) を示せ。一般項は \(\frac{1}{2}(n + 1)(n + 2)z^{n}\) となる。
-
指数が負の整数のときの二項定理: \(|z| \lt 1\) で \(m\) が正の整数なら \[ \frac{1}{(1 - z)^{m}} = 1 + mz + \frac{m(m + 1)}{1·2} z^{2} + \cdots + \frac{m(m + 1) \cdots (m + n - 1)}{1·2 \cdots n} z^{n} + \cdots \] が成り立つ。
[\(m\) より小さい全ての \(m\) でこの定理が成り立つと仮定する。このとき問題 2 から次に示す \(s_{n}\) に対して \(1/(1 - z)^{m+1} = \sum s_{n}z^{n}\) が分かる: \[ \begin{aligned} s_{n} & = 1 + m + \frac{m(m + 1)}{1·2} + \cdots + \frac{m(m + 1) \cdots (m + n - 1)}{1·2 \cdots n} \\ & = \frac{(m + 1)(m + 2) \cdots (m + n)}{1·2 \cdots n} \end{aligned} \] この変形は帰納法の仮定から簡単に示せる]
-
級数の積の計算を使って、 \[ f(m, z) = 1 + \binom{m}{1} z + \binom{m}{2} z^{2} + \cdots \] に対して \(|z| \lt 1\) なら \(f(m, z)f(m', z) = f(m + m', z)\) が成り立つと示せ。 [この等式はオイラーによる二項定理の証明の根幹をなす。右辺の積における \(z^{n}\) の係数は \[ \binom{m'}{n} + \binom{m}{1} \binom{m'}{n - 1} + \binom{m}{2} \binom{m'}{n - 2} + \cdots + \binom{m}{n - 1} \binom{m'}{1} + \binom{m}{n} \] となる。
これは \(m\) と \(m'\) に関する多項式であり、\(m\) と \(m'\) が正の整数なら \(\dbinom{m + m'}{k}\) に等しいことが指数が正の整数の場合の二項定理から分かる。そして \(m\) と \(m'\) に関する二つの多項式が全ての正整数 \(m\) と \(m'\) に対して等しいなら、それらは恒等的に等しい]
-
\(f(z) = 1 + z + \dfrac{z^{2}}{2!} + \cdots\) なら \(f(z)f(z') = f(z + z')\) が成り立つ。 [\(f(z)\) の級数は全ての \(z\) で絶対収束する。\(u_{n} = \dfrac{z^{n}}{n!},\ v_{n} = \dfrac{{z'}^{n}}{n!}\) なら \(w_{n} = \dfrac{(z + z')^{n}}{n!}\) となることは容易に分かる]
-
もし \[ C(z) = 1 - \frac{z^{2}}{2!} + \frac{z^{4}}{4!} - \cdots,\quad S(z) = z - \frac{z^{3}}{3!} + \frac{z^{5}}{5!} - \cdots \] なら \[ C(z + z') = C(z)C(z') - S(z)S(z'),\quad S(z + z') = S(z)C(z') + C(z)S(z') \] かつ \[ \{C(z)\}^{2} + \{S(z)\}^{2} = 1 \] が成り立つ。
-
級数の積が計算できない場合: \(\sum u_{n}\) と \(\sum v_{n}\) が絶対収束しない場合には級数の積の計算に関する結果が成り立たないことは、次の例を見ればわかる: \[ u_{n} = v_{n} = \frac{(-1)^{n}}{\sqrt{n + 1}} \] このとき \[ w_{n} = (-1)^{n} \sum_{r=0}^{n} \frac{1}{\sqrt{(r + 1)(n + 1 - r)}} \] だが、\(\sqrt{(r + 1)(n + 1 - r)} \leq \frac{1}{2}(n + 2)\) より \(|w_{n}| \gt (2n + 2)/(n + 2) \to 2\) となる。つまり \(\sum w_{n}\) は収束しない。
第八章に関するその他の例
-
\(\sum n^{k}\{\sqrt{n + 1} - 2\sqrt{n} + \sqrt{n - 1}\}\) の収束性を議論せよ。\(k\) は実数とする。
(Math. Trip. 1890.)
-
次の級数を考える: \[ \sum n^{r} \Delta^{k}(n^{s}) \] ここで \[ \Delta u_{n} = u_{n} - u_{n+1},\quad \Delta^{2} u_{n} = \Delta(\Delta u_{n}) \] などとする。この級数が収束するのは \(k \gt r + s + 1\) のときに限ると示せ。ただし \(s\) が \(k\) より小さい正の整数のときは級数が \(0\) となるので、この場合は除く。
[第七章に関するその他の例 11 の結果から、\(\Delta^{k}(n^{s})\) が一般に \(n^{s-k}\) と同じオーダーにあることが分かる]
-
次を示せ: \[ \sum_{1}^{\infty} \frac{n^{2} + 9n + 5}{(n + 1)(2n + 3)(2n + 5)(n + 4)} = \frac{5}{36} \]
(Math. Trip. 1912.)
[一般項を部分分数で表す]
-
任意の \(n\) の有理関数 \(R(n)\) に対して、とある多項式 \(P(n)\) と定数 \(A\) に対する \(\sum \{R(n) - P(n) - (A/n)\}\) が収束すると示せ。特殊ケースとして \(R(n)\) が \(1/(an + b)\) および \((an^{2} + 2bn + c)/(\alpha n^{2} + 2\beta n + \gamma)\) である場合を考えよ。
-
級数 \[ 1 - \frac{1}{1 + z} + \frac{1}{2} - \frac{1}{2 + z} + \frac{1}{3} - \frac{1}{3 + z} + \cdots \] が収束すると示せ。ただし \(z\) が負の整数である場合は除く。
-
次の級数の収束と発散を調べよ: \[ \begin{gathered} \sum \sin\frac{a}{n},\quad \sum \frac{1}{n} \sin\frac{a}{n},\quad \sum (-1)^{n} \sin\frac{a}{n},\\ \sum \left(1 - \cos\frac{a}{n}\right),\quad \sum (-1)^{n} n\left(1 - \cos\frac{a}{n}\right) \end{gathered} \] \(a\) は実数とする。
-
次の級数の収束性を議論せよ: \[ \sum_{1}^{\infty} \left(1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n}\right) \frac{\sin(n\theta + \alpha)}{n} \] \(\theta\) と \(\alpha\) は実数とする。
(Math. Trip. 1989.)
-
級数 \[ 1 - \dfrac{1}{2} - \dfrac{1}{3} + \dfrac{1}{4} + \dfrac{1}{5} + \dfrac{1}{6} - \dfrac{1}{7} - \dfrac{1}{8} - \dfrac{1}{9} - \dfrac{1}{10} + \cdots \] が収束すると示せ。符号は \(1,\ 2,\ 3,\ 4,\ \ldots\) 項ずつ変化する。符号が \(1,\ 2,\ 4,\ 8,\ \ldots\) 項ずつ変化する級数は有限に振動することを示せ。
(Math. Trip. 1908.)
-
\(u_{1},\ u_{2},\ u_{3},\ \ldots\) が単調減少の正項列で極限が \(0\) のとき、 \[ \begin{gathered} u_{1} - \dfrac{1}{2}(u_{1} + u_{2}) + \dfrac{1}{3}(u_{1} + u_{2} + u_{3}) - \cdots, \\ u_{1} - \dfrac{1}{3}(u_{1} + u_{3}) + \dfrac{1}{5}(u_{1} + u_{3} + u_{5}) - \cdots \phantom{,} \end{gathered} \] は収束する。 [\((u_{1} + u_{2} + \cdots + u_{n})/n = v_{n}\) とすれば \(v_{1},\ v_{2},\ v_{3},\ \ldots\) も単調減少の正項列であり、極限は \(0\) となる (第四章のその他の例 8, 27)。ここから一つ目の級数が収束すると分かる。二つ目の級数については読者に任せる。特に級数 \[ \begin{gathered} 1 - \dfrac{1}{2}\left(1 + \dfrac{1}{2}\right) + \dfrac{1}{3}\left(1 + \dfrac{1}{2} + \dfrac{1}{3}\right) - \cdots,\\ 1 - \dfrac{1}{3}\left(1 + \dfrac{1}{3}\right) + \dfrac{1}{5}\left(1 + \dfrac{1}{3} + \dfrac{1}{5}\right) - \cdots\phantom{,} \end{gathered} \] は収束する]
-
各項が単調減少の正項級数 \(u_{0} + u_{1} + u_{2} + \cdots\) が発散するなら \[ \frac{u_{0} + u_{2} + \cdots + u_{2n}}{u_{1} + u_{3} + \cdots + u_{2n+1}} \to 1 \] が成り立つ。
-
\(\alpha \gt 0\) なら \(\lim\limits_{p\to\infty} \sum\limits_{n=0}^{\infty} (p + n)^{-1-\alpha} = 0\) だと示せ。
-
\(\lim\limits_{\alpha\to 0+} \alpha \sum\limits_{1}^{\infty} n^{-1-\alpha} = 1\) を示せ。 [§174 から \[ 0 \lt 1^{-1-\alpha} + 2^{-1-\alpha} + \cdots + (n - 1)^{-1-\alpha} - \int_{1}^{n} x^{-1-\alpha}\, dx \leq 1 \] が分かる。ここから \(\sum n^{-1-\alpha}\) が \(\dfrac{1}{\alpha}\) と \(\dfrac{1}{\alpha} + 1\) の間にあると示せる]
-
級数 \(\sum\limits_{1}^{\infty} u_{n}\) の和を求めよ。ここで \[ u_{n} = \frac{x^{n} - x^{-n-1}}{(x^{n} + x^{-n})(x^{n+1} + x^{-n-1}) } = \frac{1}{x - 1} \left(\frac{1}{x^{n} + x^{-n}} - \frac{1}{x^{n+1} + x^{-n-1}}\right) \] であり、級数は収束する \(x\) に対して定義されるとする。
(Math. Trip. 1901.)
[\(|x|\) が \(1\) より小さいとき級数の和は \(x/\{(x - 1)(x^{2} + 1)\}\) となる。\(x = 1\) なら \(u_{n} = 0\) だから和は \(0\) で、\(x = -1\) なら \(u_{n} = \frac{1}{2}(-1)^{n+1}\) だから級数は有限に振動する]
-
次の級数が収束するときの和を求めよ: \[ \frac{z}{1 + z} + \frac{2z^{2}}{1 + z^{2}} + \frac{4z^{4}}{1 + z^{4}} + \cdots,\quad \frac{z}{1 - z^{2}} + \frac{z^{2}}{1 - z^{4}} + \frac{z^{4}}{1 - z^{8}} + \cdots \] 指数は \(2\) のべきとする。
[一つ目の級数は \(|z| \lt 1\) のときに限って収束し、和は \(z/(1 - z)\) となる。二つ目の収束は \(|z| \lt 1\) なら \(z/(1 - z)\) に収束し、\(|z| \gt 1\) なら \(1/(1 - z)\) に収束する]
-
全ての \(n\) に対して \(|a_{n}| \leq 1\) なら、方程式 \[ 0 = 1 + a_{1}z + a_{2}z^{2} + \cdots \] は絶対値が \(\frac{1}{2}\) より小さい根を持たない。唯一 \(a_{n} = -\operatorname{Cis}(n\theta)\) のときに限って根の絶対値が \(\frac{1}{2}\) となり、\(z = \frac{1}{2} \operatorname{Cis}(-\theta)\) が成り立つ。
-
再帰級数: べき級数 \(\sum a_{n}z^{n}\) が 再帰級数 (recurring series) であるとは、係数が次の関係を満たすことを言う: \[ a_{n} + p_{1}a_{n-1} + p_{2}a_{n-2} + \cdots + p_{k}a_{n-k} = 0 \qquad \text{(1)} \] ここで \(n \geq k\) であり、\(p_{1},\ p_{2},\ \ldots,\ p_{k}\) は \(n\) と独立とする。再帰級数は \(z\) の有理関数に展開できる。これを示すために、まず絶対値の十分小さい \(z\) に対して級数が収束することを見る。\(G\) を次の二つの実数の大きい方とする: \[ 1,\quad |p_{1}| + |p_{2}| + \cdots + |p_{k}| \] すると \(\text{(1)}\) から、\(n\) までの係数 \(a_{1},\ a_{2},\ \ldots a_{n}\) の絶対値の最大値を \(\alpha_{n}\) として \(|a_{n}| \leq G\alpha_{n}\) が分かる。よって \(n\) と無関係な \(K\) に対して \(|a_{n}| \lt KG^{n}\) が成り立つ。したがって考えている再帰級数は絶対値が \(1/G\) より小さい \(z\) で収束する。
一方で級数 \(f(z) = \sum a_{n}z^{n}\) に \(p_{1}z,\ p_{2}z^{2},\ \ldots,\ p_{k}z^{k}\) を乗じて足すと、関係 \(\text{(1)}\) より第 \((k - 1)\) 項より後ろの項が全て消え、次の等式が得られる: \[ (1 + p_{1}z + p_{2}z^{2} + \cdots + p_{k}z^{k})f(z) = P_{0} + P_{1}z + \cdots + P_{k-1}z^{k-1} \] \(P_{0},\ P_{1},\ \ldots,\ P_{k-1}\) は定数である。多項式 \(1 + p_{1}z + p_{2}z^{2} + \cdots + p_{k}z^{k}\) を再帰級数の関係尺度 (scale of relation) と呼ぶ。
有理関数は多項式と \(A/(z - a)^{p}\) という形の部分分数の和として表せるので、指数が負の整数のときの二項定理から、分母が \(z\) で割り切れない任意の有理関数は \(z\) の絶対値が小さいときに収束するべき級数に展開できると分かる。具体的には分母の根の絶対値の最小値 \(\rho\) に対して \(|z| \lt \rho\) なら収束する (参考: 第四章に関するその他の例 14など)。さらに一つ前の段落までの議論を逆回しにすれば、この条件を満たす級数が再帰級数であることも分かる。よってべき級数が再帰級数となる必要十分条件は、その級数が上述の条件を満たす \(\bm{z}\) の有理関数の展開となることである。
-
差分方程式の解: 問題 16 の \(\text{(1)}\) のような関係式を \(\bm{a_{n}}\) に関する定数係数の線形差分方程式 (linear difference-equation in \(a_{n}\) with constant coefficients) と呼ぶ。この方程式の解法は例を示せば十分に説明できる。方程式 \[ a_{n} - a_{n-1} - 8a_{n-2} + 12a_{n-3} = 0 \] を考える。再帰べき級数 \(\sum a_{n}z^{n}\) を考えると、問題 16 と同様の方法でこの和が \[ \frac{a_{0} + (a_{1} - a_{0}) z + (a_{2} - a_{1} - 8a_{0}) z^{2}} {1 - z - 8z^{2} + 12z^{3}} = \frac{A_{1}}{1 - 2z} + \frac{A_{2}}{(1 - 2z)^{2}} + \frac{B}{1 + 3z} \] だと分かる。ここで \(A_{1},\ A_{2},\ B\) の \(a_{0},\ a_{1},\ a_{2}\) を使った表現は簡単に求まる。分数をそれぞれ個別に展開すれば、\(z^{n}\) の係数を得る: \[ a_{n} = 2^{n}\{A_{1} + (n + 1) A_{2}\} + (-3)^{n} B \] \(A_{1},\ A_{2},\ B\) の値は最初の三つの係数 \(a_{0},\ a_{1},\ a_{2}\) に依存しており、もちろん \(a_{0},\ a_{1},\ a_{2}\) の値に制限はない。
-
差分方程式 \(u_{n} - 2\cos\theta u_{n-1} + u_{n-2} = 0\) の解は \(u_{n} = A\cos n\theta + B\sin n\theta\) である。\(A\) と \(B\) は任意定数を表す。
-
\(u_{n}\) が \(n\) の \(k\) 次多項式なら \(\sum u_{n} z^{n}\) は再帰級数であり、関係尺度は \((1 - z)^{k+1}\) である。
(Math. Trip. 1904.)
-
\(\dfrac{9}{(z - 1)(z + 2)^{2}}\) を \(z\) の昇べきに展開せよ。
(Math. Trip. 1913.)
-
\(\dfrac{z}{1 + z + z^{2}}\) を \(z\) のべき級数に展開したときの \(z^{n}\) の係数を \(f(n)\) とする。このとき \[ \text{(1)}\ f(n) + f(n - 1) + f(n - 2) = 0,\quad \text{(2)}\ f(n) = \frac{\omega_{3}^{n} - \omega_{3}^{2n}}{\omega_{3} - \omega_{3}^{2}} \] を示せ。\(\omega_{3}\) は \(1\) の複素三重根とする。\(n\) が \(3k,\ 3k + 1,\ 3k + 2\) のとき \(f(n)\) が \(0,\ 1,\ -1\) だと示し、この等式から \(z/(1 + z + z^{2}) = z(1 - z)/(1 - z^{3})\) を導け。
-
プレイヤーがコインを投げ、表が出たら二点、裏が出たら一点を獲得する。点数が \(n\) 以上になるまでコインを投げ続けるとき、総得点がちょうど \(n\) になる確率が \(\frac{1}{3}\{2 + (-\frac{1}{2})^{n}\}\) だと示せ。
(Math. Trip. 1898.)
[確率を \(p_{n}\) とすれば \(p_{n} = \frac{1}{2} (p_{n-1} + p_{n-2})\) が成り立つ。また \(p_{0} = 1,\ p_{1} = \frac{1}{2}\) である]
-
次を示せ: \[ \frac{1}{a + 1} + \frac{1}{a + 2} + \cdots + \frac{1}{a + n} = \binom{n}{1}\frac{1}{a + 1} - \binom{n}{2}\frac{1!}{(a + 1)(a + 2)} + \cdots \] \(n\) は正の整数で、\(a\) は \(-1,\ -2,\ \ldots,\ -n\) のいずれでもないとする。
[右辺の項を部分分数に展開すれば示せる。\(a \gt -1\) なら、この結果は次の等式から簡単に得られる: \[ \int_{0}^{1} x^{a}\frac{1 - x^{n}}{1 - x}\, dx = \int_{0}^{1} (1 - x)^{a}\{1 - (1 - x)^{n}\}\frac{dx}{x} \] 証明するには \((1 - x^{n})/(1 - x)\) と \(1 - (1 - x)^{n}\) を \(x\) のべき級数で表し、各項を個別に積分する。この結果は代数的な恒等式であり、\(-1,\ -2,\ \ldots,\ -n\) を除いた全ての \(a\) で成り立つ]
-
級数の乗算を使って次を示せ: \[ \sum_{0}^{\infty} \frac{z^{n}}{n!} \sum_{1}^{\infty} \frac{(-1)^{n-1}z^{n}}{n·n!} = \sum_{1}^{\infty} \left(1 + \frac{1}{2} + \frac{1}{3} + \cdots + \frac{1}{n}\right) \frac{z^{n}}{n!} \]
[\(z^{n}\) の係数は \[ \frac{1}{n!}\left\{ \binom{n}{1} - \frac{1}{2}\binom{n}{2} + \frac{1}{3}\binom{n}{3} - \cdots \right\} \] となるので、問題 23 で \(a = 0\) としたものを使う]
-
\(n \to \infty\) で \(A_{n} \to A\) および \(B_{n} \to B\) なら \[ \frac{A_{1}B_{n} + A_{2}B_{n-1} + \cdots + A_{n}B_{1}}{n} \to AB \] が成り立つ。
[\(A_{n} = A + \varepsilon_{n}\) とすると、この式は \[ A \frac{B_{1} + B_{2} + \cdots + B_{n}}{n} + \frac{\varepsilon_{1}B_{n} + \varepsilon_{2}B_{n-1} + \cdots + \varepsilon_{n}B_{1}}{n} \] に等しい。
一つ目の項は \(AB\) に向かう (第四章に関するその他の例 27)。\(|B_{\nu}|\) の最大値より大きい適当な実数を \(\beta\) とすると、二つ目の項の絶対値は \(\beta\{|\varepsilon_{1}| + |\varepsilon_{2}| + \cdots + |\varepsilon_{n}|\}/n\) より小さい。よって二つ目の項は \(0\) に向かう]
-
\(c_{n} = a_{1}b_{n} + a_{2}b_{n-1} + \cdots + a_{n}b_{1}\) で \[ \begin{gathered} A_{n} = a_{1} + a_{2} + \cdots + a_{n},\\ B_{n} = b_{1} + b_{2} + \cdots + b_{n},\\ C_{n} = c_{1} + c_{2} + \cdots + c_{n}\hphantom{,} \end{gathered} \] なら \[ C_{n} = a_{1}B_{n} + a_{2}B_{n-1} + \cdots + a_{n}B_{1} = b_{1}A_{n} + b_{2}A_{n-1} + \cdots + b_{n}A_{1} \] および \[ C_{1} + C_{2} + \cdots + C_{n} = A_{1}B_{n} + A_{2}B_{n-1} + \cdots + A_{n}B_{1} \] だと示せ。
この結果を使って、\(\sum a_{n}\) と \(\sum b_{n}\) が収束して和が \(A\) と \(B\) のとき、つまり \(A_{n} \to A,\ \) \(B_{n} \to B\) のとき \[ \frac{C_{1} + C_{2} + \cdots + C_{n}}{n} \to AB \] だと示せ。さらに \(\bm{c_{n}}\) が収束するなら和は \(\bm{AB}\) であることを導け。この結果は級数の積に関するアーベルの定理として知られる。級数 \(\sum a_{n}\) と \(\sum b_{n}\) が絶対収束するならこの方法で積が計算できることは前に見たが、アーベルの定理によると一方あるいは両方が絶対収束せずとも、積の級数が収束することさえ分かれば、この方法で積が計算できる。
-
次を示せ: \[ \begin{aligned} \dfrac{1}{2} \left(1 - \dfrac{1}{2} + \dfrac{1}{3} - \cdots\right)^{2} & = \dfrac{1}{2} - \dfrac{1}{3} \left(1 + \dfrac{1}{2}\right) + \dfrac{1}{4} \left(1 + \dfrac{1}{2} + \dfrac{1}{3}\right) - \cdots,\\ \dfrac{1}{2} \left(1 - \dfrac{1}{3} + \dfrac{1}{5} - \cdots\right)^{2} & = \dfrac{1}{2} - \dfrac{1}{4} \left(1 + \dfrac{1}{3}\right) + \dfrac{1}{6} \left(1 + \dfrac{1}{3} + \dfrac{1}{5}\right) - \cdots \end{aligned} \]
[級数の収束性を示すには問題 9 を使う]
-
積分 \(\displaystyle\int_{0}^{\pi} \sin^{m} x (1 - \cos x)^{n}\, dx\) が収束するのは \(m\) と \(n\) がどんな値のときか? [\(m + 1\) と \(m + 2n + 1\) が正のとき]
-
\(a \gt 1\) で次の等式が成り立つと示せ: \[ \int_{-1}^{1} \frac{dx}{(a - x) \sqrt{1 - x^{2}}} = \frac{\pi}{\sqrt{a^{2} - 1}} \]
-
次の等式を示せ: \[ \begin{alignedat}{2} \int_{0}^{\infty} F\{\sqrt{x^{2} + 1} + x\}\, dx & = \dfrac{1}{2}\int_{1}^{\infty} & & \left(1 + \frac{1}{y^{2}}\right) F(y) \, dy,\\ \int_{0}^{\infty} F\{\sqrt{x^{2} + 1} - x\}\, dx & = \dfrac{1}{2}\int_{0}^{1} & & \left(1 + \frac{1}{y^{2}}\right) F(y)\, dy \end{alignedat} \] 特に \(n \gt 1\) なら次の等式が成り立つと示せ: \[ \int_{0}^{\infty} \frac{dx}{\{\sqrt{x^{2} + 1} + x\}^{n}} = \int_{0}^{\infty} \{\sqrt{x^{2} + 1} - x\}^{n}\, dx = \frac{n}{n^{2} - 1} \]
[この例およびこれからの例では、積分が §177 からの議論で考えた意味を持つような関数だけが積分記号の中に生じるとする]
-
\(a\) と \(b\) が正の実数で \(2y = ax - (b/x)\) なら、\(x\) が \(0\) から \(\infty\) まで増加するとき \(y\) が \(-\infty\) から \(\infty\) に増加すると示せ。これを使って \[ \begin{aligned} \int_{0}^{\infty} f\left\{\dfrac{1}{2}\left(ax + \frac{b}{x}\right)\right\} dx & = \frac{1}{a} \int_{-\infty}^{\infty} f\{\sqrt{y^{2} + ab}\} \left\{1 + \frac{y}{\sqrt{y^{2} + ab}}\right\} dy\\ & = \frac{2}{a} \int_{0}^{\infty} f\{\sqrt{y^{2} + ab}\}\, dy \end{aligned} \] を示せ。
-
\(a\) と \(b\) が正の実数で \(2y = ax + (b/x)\) なら、\(\sqrt{ab}\) より大きい任意の \(y\) には二つの \(x\) が対応すると示せ。二つの \(x\) の大きい方を \(x_{1}\) として小さい方を \(x_{2}\) とすると、\(y\) が \(\sqrt{ab}\) から \(\infty\) に増加するとき \(x_{1}\) は \(\sqrt{b/a}\) から \(\infty\) に増加し、\(x_{2}\) は \(\sqrt{b/a}\) から \(0\) に減少すると示せ。さらに \[ \begin{aligned} \int_{\sqrt{b/a}}^{\infty} f(y)\, dx_{1} & = \frac{1}{a} \int_{\sqrt{ab}}^{\infty} f(y) \left\{\frac{y}{\sqrt{y^{2} - ab}} + 1\right\} dy,\\ \int_{0}^{\sqrt{b/a}} f(y)\, dx_{2} & = \frac{1}{a} \int_{\sqrt{ab}}^{\infty} f(y) \left\{\frac{y}{\sqrt{y^{2} - ab}} - 1\right\} dy \end{aligned} \] および \[ \int_{0}^{\infty} f\left\{\dfrac{1}{2}\left(ax + \frac{b}{x}\right)\right\} dx = \frac{2}{a} \int_{\sqrt{ab}}^{\infty} \frac{yf(y)}{\sqrt{y^{2} - ab}}\, dy = \frac{2}{a} \int_{0}^{\infty} f\{\sqrt{z^{2} + ab}\}\, dz \] を導け。
-
次の等式を示せ: \[ \int_{0}^{\pi} f(\sec\dfrac{1}{2}x + \tan\dfrac{1}{2}x)\frac{dx}{\sqrt{\sin x}} = \int_{0}^{\pi} f(\cosec x)\frac{dx}{\sqrt{\sin x}} \]
-
\(a\) と \(b\) が正なら \[ \int_{0}^{\infty} \frac{dx}{(x^{2} + a^{2})(x^{2} + b^{2})} = \frac{\pi}{2ab(a + b)},\quad \int_{0}^{\infty} \frac{x^{2}\, dx}{(x^{2} + a^{2})(x^{2} + b^{2})} = \frac{\pi}{2(a + b)} \] が成り立つ。これを使って、\(\alpha,\ \beta,\ \gamma\) が正で \(\beta^{2} \geq \alpha\gamma\) なら \[ \int_{0}^{\infty} \frac{dx}{\alpha x^{4} + 2\beta x^{2} + \gamma} = \frac{\pi}{2\sqrt{2\gamma A}}, \quad \int_{0}^{\infty} \frac{x^{2}\, dx}{\alpha x^{4} + 2\beta x^{2} + \gamma} = \frac{\pi}{2\sqrt{2\alpha A}} \] で \(A = \beta + \sqrt{\alpha\gamma}\) だと示せ。さらに \(f(y) = 1/(c^{2} + y^{2})\) として問題 31 の結果を導け。最後の二つの結果は \(\beta^{2} \lt \alpha\gamma\) でも正しいが、その場合の証明は難しい。
-
\(b\) が正なら \[ \int_{0}^{\infty} \frac{x^{2}\, dx}{(x^{2} - a^{2})^{2} + b^{2}x^{2}} = \frac{\pi}{2b},\quad \int_{0}^{\infty} \frac{x^{4}\, dx}{\{(x^{2} - a^{2})^{2} + b^{2}x^{2}\}^{2}} = \frac{\pi}{4b^{3}} \] だと示せ。
-
シュワルツの不等式 (第七章に関するその他の例 42) を第一種および第二種の無限積分に拡張せよ。
-
§178 の終わりで考えた関数を \(\phi(x)\) とする。このとき \[ \int_{0}^{\infty} \phi(x)\, dx = \sum_{0}^{\infty} \frac{1}{(n + 1)^{2}} \] を示せ。
-
次を示せ: \[ \begin{alignedat}{2} \int_{1}^{\infty} dx \left(\int_{1}^{\infty} \frac{x - y}{(x + y)^{3}}\, dy\right) & = -1, \quad & \int_{1}^{\infty} dy \left(\int_{1}^{\infty} \frac{x - y}{(x + y)^{3}}\, dx\right) & = 1;\\ \int_{1}^{\infty} dx \left(\int_{1}^{\infty} \frac{x^{2} - y^{2}}{(x^{2} + y^{2})^{2}}\, dy\right) & = -\dfrac{1}{4}\pi, \quad & \int_{1}^{\infty} dy \left(\int_{1}^{\infty} \frac{x^{2} - y^{2}}{(x^{2} + y^{2})^{2}}\, dx\right) & = \dfrac{1}{4}\pi \end{alignedat} \]
積分区間が \(0\) から \(1\) のときに対する同様の結果を示せ。
(Math. Trip. 1913.)
-
級数の表記を (第四章のように) \(u_{1} + u_{2} + \cdots\) としようと (ここでしたように) \(u_{0} + u_{1} + \cdots\) としようと、本質的にはもちろん何も変わらない。ただ本章の後半で扱う \(a_{0} + a_{1}x + a_{2}x^{2} + \cdots\) という形の級数では後者の方が分かりやすい。そのため \(u_{0} + u_{1} + \cdots\) を標準的な記法として採用する。しかしこの表記に固執するわけではなく、初項を \(u_{1}\) にした方が考えやすいならそうすることもある。例えば級数 \(1 + \frac{1}{2} + \frac{1}{3} + \cdots\) を扱うときには、\(u_{n} = 1/n\) として級数が \(u_{1}\) から始まるとした方が、\(u_{n} = 1/(n + 1)\) として級数が \(u_{0}\) から始まるとするよりも考えやすい。この指摘は他に 例 68.4 にも当てはまる。[return]
-
これ以降 "正" には \(0\) を含める。[return]
-
この章では \(r\) は常に正または \(0\) とする。[return]
-
この定理はディリクレによって 1837 年に初めてはっきりと述べられたようだが、それ以前の学者 (特にコーシー) に知られていたのは間違いない。[return]
-
問題 2–4 ではこれまでと同じように正項級数を考える。[return]
-
最初の五項を取ると \(\sum n^{-12}\) は小数点以下第七位まで正しくなるが、\(\sum n^{-2}\) をこれと同じ精度で近似するにはおよそ \(10,000,000\) 個の項が必要になる。本章の数値的な結果の多くは拙著 "Orders of Infinity" (Cambridge Math. Tracts, No. 12) の (J・ジャクソン氏によってまとめられた) Appendix III にある。[return]
-
この定理はアーベルによって発見されたがその後忘れられ、プリングスハイムによって再発見された。[return]
-
Bromwich, Infinite Series, pp. 225 et seq. および Plane Trigonometry, (3rd edition), pp. 268 et seq. を参照。[return]