§197 対数関数の定義

\(x\) の対数 \(\log x\) は次の等式で定義される: \[ \log x = \int_{1}^{x} \frac{dt}{t} \] 例 76.2 からは積分範囲が \(x = 0\) を含むときこの積分が意味を持たないと分かるので、\(x\) は正である必要がある。積分の下端は \(1\) でなくても構わないが、\(1\) とすれば \(\log 1 = 0\) となるので都合がいい。

では \(x\) が \(0\) から \(\infty\) まで変化するときの \(\log x\) の振る舞いを考えよう。\(\log x\) が \(x\) の連続関数であり、\(x\) に関して単調増加であり、次の導関数を持つことが定義から直ちに従う: \[ D_{x} \log x = \frac{1}{x} \] さらに §175 から \(x \to \infty\) のとき \(\log x\) が \(\infty\) に向かうと分かる。

\(x\) が \(1\) より小さい正の実数のとき \(\log x\) は負となる。これは \[ \log x = \int_{1}^{x} \frac{dt}{t} = -\int_{x}^{1} \frac{dt}{t} \lt 0 \] から従う。さらにこの積分で \(t = 1/u\) と置換すると \[ \log x = \int_{1}^{x} \frac{dt}{t} = -\int_{1}^{1/x} \frac{du}{u} = -\log \dfrac{1}{x} \] を得る。つまり \(x\) が \(1\) から \(0\) へ減少するとき \(\log x\) は単調に \(-\infty\) へ向かう。

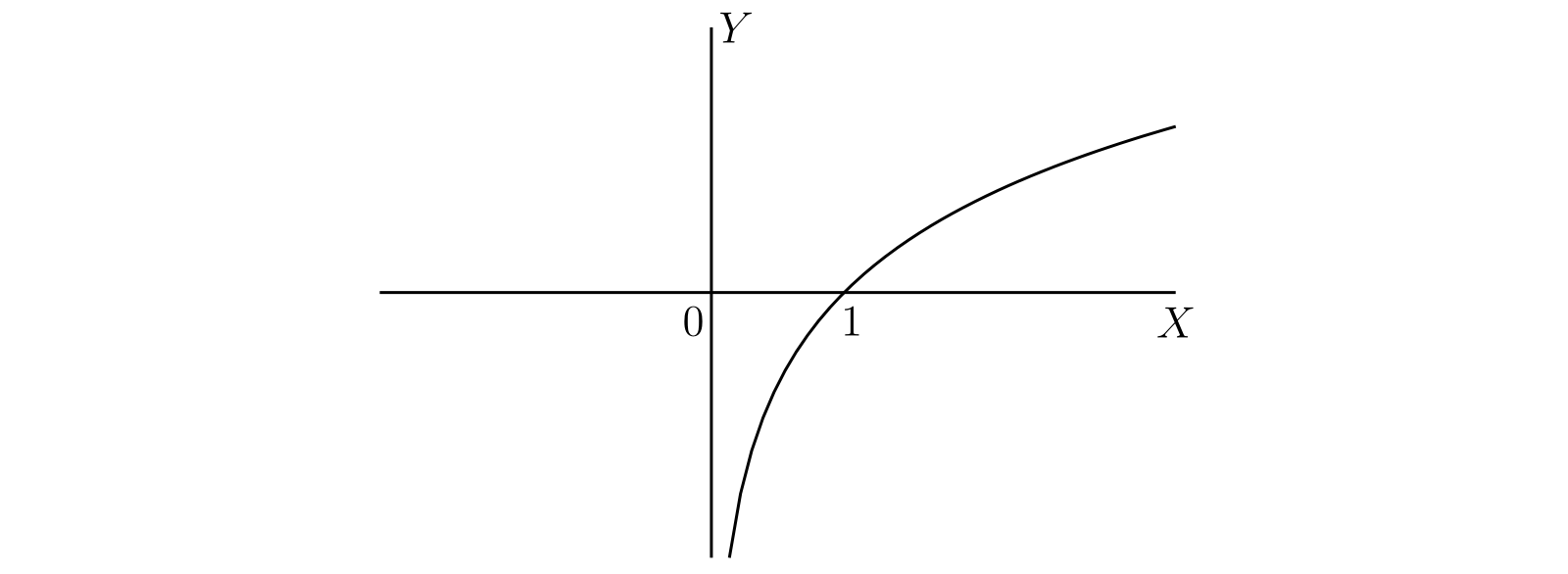
対数関数のグラフの概形を 図 52 に示す。\(\log x\) の導関数は \(1/x\) だから、曲線の傾きは \(x\) が大きいとき非常になだらかで、\(x\) が小さいとき非常に急になる。