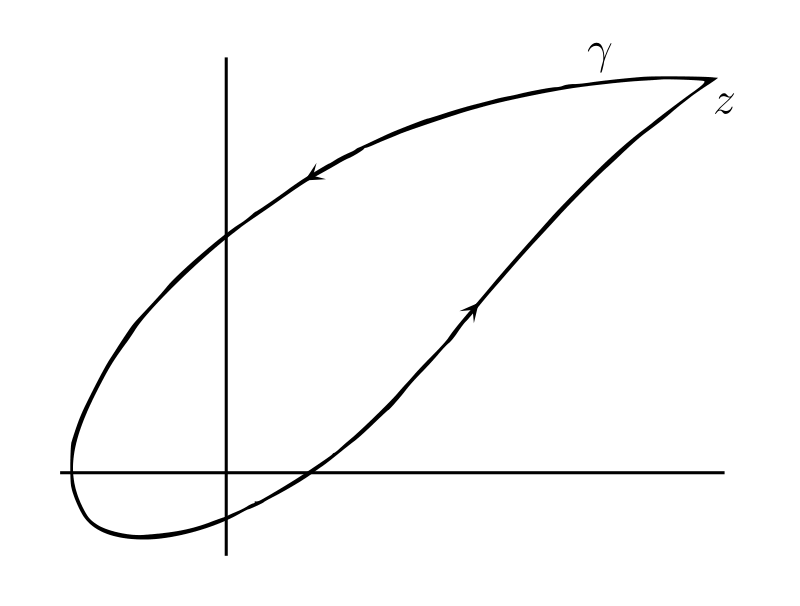補遺一 全ての多項式が根を持つことの証明

実数または複素数を係数とする \(z\) の多項式 \[ Z = P(z) = \alpha_{0} z^{n} + \alpha_{1} z^{n-1} + \cdots + \alpha_{n} \] を考える。\(z\) および \(Z\) の値はそれぞれ平面上に表せるから、二つの平面をそれぞれ \(z\) 平面および \(Z\) 平面と呼ぶ。\(z\) が \(z\) 平面における閉曲線 \(\gamma\) をたどるとき、\(Z\) は \(Z\) 平面における閉曲線 \(\Gamma\) をたどることが分かる。まずは \(\Gamma\) が原点を通らないと仮定する。

任意の \(Z\) は無限個の \(\arg Z\) を持ち、それらは \(2\pi\) の倍数だけ離れている。さらに \(Z\) が \(\Gamma\) 上を動くとき、全ての \(\arg Z\) は連続的に変化する¹。よって最初の \(Z\) に対応する偏角を一つ選び、\(Z\) が \(\Gamma\) に沿って動くときに連続的に変化する偏角の値を追うことで、\(\Gamma\) 上の全ての点に対する特定の \(\arg Z\) を選択できる。ここからの議論では "\(Z\) の偏角" という言葉および記号 \(\arg Z\) をこうして選択した \(Z\) の偏角に対して使うことにする。つまり \(\arg Z\) は \(Z\) の実部 \(X\) と虚部 \(Y\) の連続な一価関数を表す。

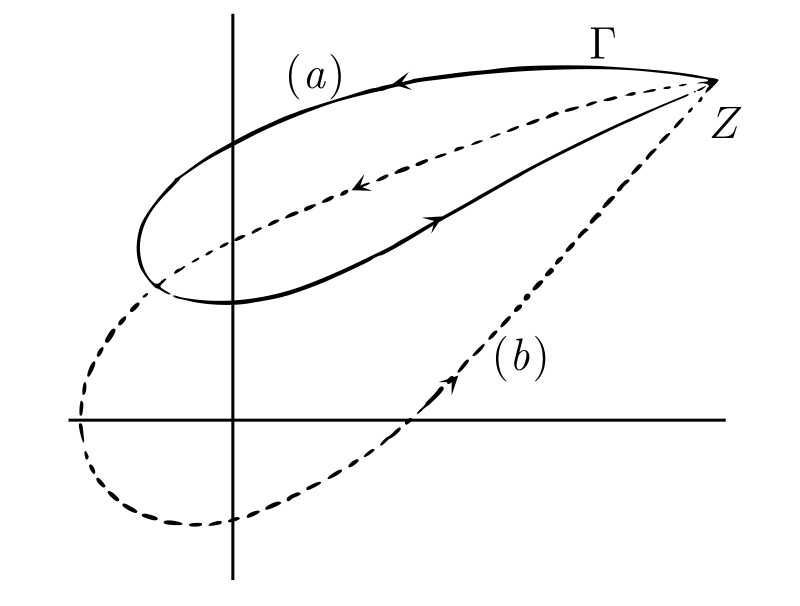
\(Z\) が \(\Gamma\) を通って最初の点に戻ってくるときの偏角を考える。\(\Gamma\) の中に原点を含まない 図 B の (a) のような場合には最後の \(Z\) の偏角が最初と同じになるが、その他の場合には最後の \(Z\) の偏角が最初の偏角より \(2\pi\) の倍数だけ大きくなる。例えば \(\Gamma\) が原点を正方向に一度回る 図 B の (b) のような場合には最後の偏角が \(2\pi\) だけ大きくなる。この関係は \(\Gamma\) だけではなく \(Z\) 平面上の原点を通らない任意の閉曲線で成り立つ。つまりこれらの閉曲線には「\(Z\) が曲線をたどるときの \(\arg Z\) の増分」とでも呼ぶべき数が存在する。この数は \(Z\) の初期位置や初期位置における偏角の値の選択によって変化しない。

これから \(\bm{Z}\) が最初の点に戻ってきたときに \(\bm{Z}\) の偏角が変わっているなら、\(\bm{\gamma}\) 上または \(\bm{\gamma}\) の内部の点で \(\bm{Z = 0}\) となることを示す。

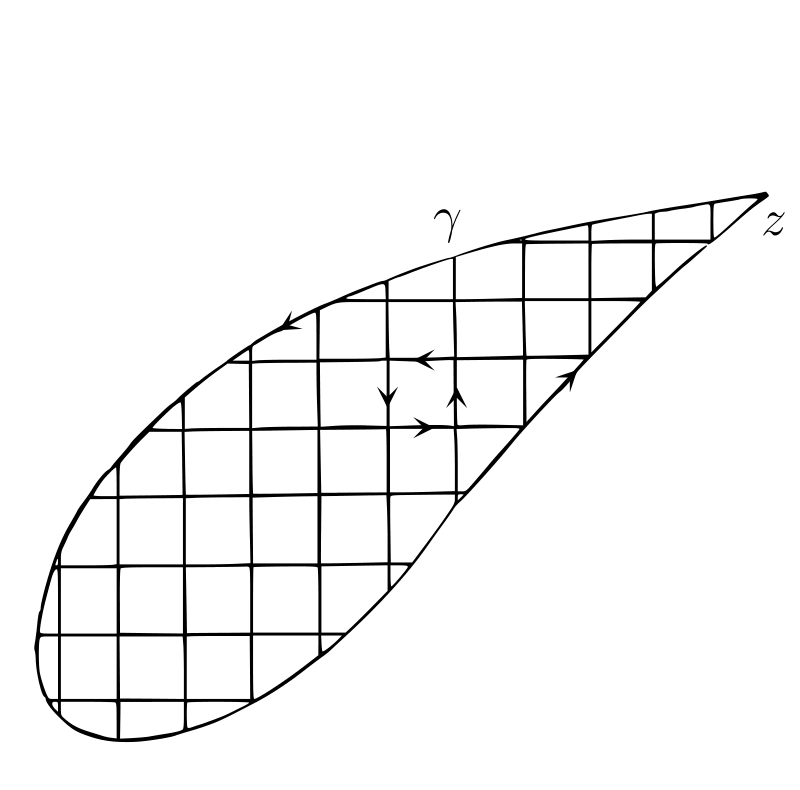
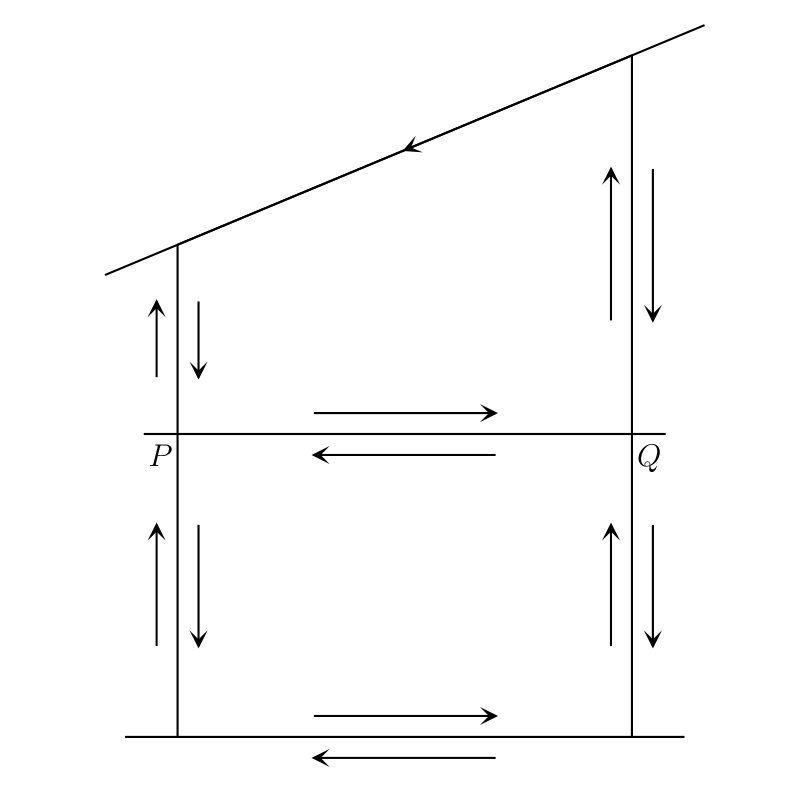
図 C のように、軸に平行で \(\delta_{1}\) だけ離れた直線を使って \(\gamma\) をたくさんの小さな閉曲線に分割する²。もしこれらの小閉曲線上で \(Z = 0\) となるなら証明したい条件が成り立つので、そうならないと仮定する。このとき \(z\) が \(\gamma\) をたどるときの \(\arg Z\) の増分は、\(z\) が全ての小閉曲線を別々にたどるときの増分の和に等しい。証明は次の通り。\(z\) が全ての小閉曲線を同じ方向にたどるとき、最終的に \(z\) は閉曲線 \(\gamma\) を一度だけたどり、その他の軸に平行な直線は逆方向に一度ずつたどる。つまり \(z\) は図中の \(PQ\) を \(P\) から \(Q\) へ一度、\(Q\) から \(P\) へ一度通過する。\(z\) が \(P\) から \(Q\) へ動くとき、仮定より \(Z\) は原点を通らないので、\(\arg Z\) は連続的に変化する。このときの \(\arg Z\) の増分を \(\theta\) とすれば、\(z\) が \(Q\) から \(P\) へ動くときの増分は \(-\theta\) となる。よって \(\arg Z\) の増分を全て足せば、小閉曲線からの寄与は全て打ち消され、\(\gamma\) からの寄与だけが残る。

したがって、もし \(z\) が \(\gamma\) をたどるときに \(\arg Z\) が変化するなら、小閉曲線 \(\gamma_{1}\) であって \(z\) が \(\gamma_{1}\) をたどるときに \(\arg Z\) が変化するものが少なくとも一つ存在する。この小閉曲線 \(\gamma_{1}\) は追加で引いた軸に平行な直線からなる正方形の可能性もあるし、そういった直線と \(\gamma\) の一部からなる閉曲線の可能性もある。いずれの場合でも閉曲線 \(\gamma_{1}\) の境界上または内部の任意の点は、辺の長さが \(\delta_{1}\) で軸に平行な正方形 \(\Delta_{1}\) の中に収まる。

続いて軸に平行で幅が \(\delta_{2} \lt \delta_{1}\) である直線で \(\gamma_{1}\) をさらに分割すれば、分割された閉曲線 \(\gamma_{2}\) であって \(z\) が \(\gamma_{2}\) をたどるとき \(\arg Z\) が変化するものが存在する。このとき \(\gamma_{2}\) は一辺の長さが \(\delta_{2}\) の正方形 \(\Delta_{2}\) に完全に含まれ、\(\Delta_{2}\) は \(\Delta_{1}\) に含まれる。

さて \(\delta_{1},\ \delta_{2},\ \ldots,\ \delta_{m},\ \ldots\) という極限が \(0\) の無限減少列を取る³。上の議論を繰り返すことで、正方形の列 \(\Delta_{1},\ \Delta_{2},\ \ldots,\ \Delta_{m},\ \ldots\) および閉曲線の列 \(\gamma_{1},\ \gamma_{2},\ \ldots,\ \gamma_{m},\ \ldots\) であって (i) \(\Delta_{m+1}\) は \(\Delta_{m}\) の内部に完全に含まれ、(ii) \(\gamma_{m}\) は \(\Delta_{m}\) の内部に完全に含まれ、(iii) \(z\) が \(\gamma_{m}\) をたどるとき \(\arg Z\) が変化するものが存在すると示せる。

\(\Delta_{m}\) の左下と右上の座標を \((x_{m}, y_{m})\) および \((x_{m} + \delta_{m}, y_{m} + \delta_{m})\) とすると、明らかに \(x_{1},\ x_{2},\ \ldots,\ x_{m},\ \ldots\) は増加列そして \(x_{1} + \delta_{1},\ x_{2} + \delta_{2},\ \ldots,\ x_{m} + \delta_{m},\ \ldots\) は減少列となり、共通の極限 \(x_{0}\) が存在する。同様に \(y_{m}\) と \(y_{m} + \delta_{m}\) は共通の極限 \(y_{0}\) を持ち、\((x_{0}, y_{0})\) は全ての正方形 \(\Delta_{m}\) に含まれる唯一の点である。つまりどれだけ小さい \(\delta\) を考えても、\((x_{0}, y_{0})\) を含む辺が軸に平行で長さが \(\delta\) の正方形であって、その中のある閉曲線の上を \(z\) がたどるとき \(\arg Z\) が変化するものが存在する。

ここまでくれば \[ P(x_{0} + iy_{0}) = 0 \] を背理法で示せる。\(P(x_{0} + iy_{0}) = a\) で \(|a| = \rho \gt 0\) と仮定する。\(P(x + iy)\) は \(x\) と \(y\) の連続関数だから、\((x_{0}, y_{0})\) を中心とした辺が軸に平行な正方形であって \[ |P(x + iy) - P(x_{0} + iy_{0})| \lt \dfrac{1}{2}\rho \] が \(x + iy\) の内部および境界で成り立つものを取れる。この全ての点で \[ P(x + iy) = a + \phi \] とすれば \(|\phi| \lt \frac{1}{2}\rho\) である。この正方形の中に収まる任意の閉曲線を考えると、\(z\) がこの閉曲線をたどるとき \(Z = a + \phi\) も閉曲線をたどる。しかしこのとき \(Z\) は中心が \(a\) で半径が \(\frac{1}{2}\rho\) の円の内部に常にあり、この円は原点を含まない。よって \(Z\) の偏角は変化しない。

しかしこれは上で示した結果、つまり全ての正方形 \(\Delta_{m}\) の中には \(z\) がたどると \(\arg Z\) が変化する閉曲線が存在するという結果と矛盾する。したがって \(P(x_{0} + iy_{0}) = 0\) が成り立つ。

よって後は \(z\) 平面上の閉曲線 \(\gamma\) であって \(z\) が \(\gamma\) をたどるときに \(\arg Z\) が変化するものが常に一つ見つけられることを示せばよい。さて \[ Z = a_{0} z^{n} \left(1 + \frac{a_{1}}{a_{0}z} + \frac{a_{2}}{a_{0} z^{2}} + \cdots + \frac{a_{n}}{a_{0} z^{n}}\right) \] であり、次の条件を満たす \(R\) を見つけられる: \[ \frac{|a_{1}|}{|a_{0}| R} + \frac{|a_{2}|}{|a_{0}| R^{2}} + \cdots + \frac{|a_{n}|}{|a_{0}| R^{n}} \lt \delta \] ここで \(\delta\) は正の実数であり、どれだけ小さくても構わない。もし \(\gamma\) が原点中心で半径 \(R\) の円なら、\(\gamma\) 上の任意の点で \[ Z = a_{0} z^{n} (1 + \rho) \] が成り立つ。ここで \(|\rho| \lt \delta\) である。このとき上と同じ議論で、\(z\) が \(\gamma\) を正方向にたどるとき \(\arg(1 + \rho)\) が変化しないことを証明でき、その一方で \(\arg z^{n}\) は \(2n\pi\) だけ増える。よって \(\arg Z\) は \(2n\pi\) だけ変化するので、\(Z = 0\) が根を持つことの証明が完了する。

ここまでは \(\Gamma\) および \(\Gamma\) を分割して得られる小閉曲線がどれも原点を通らないと仮定してきた。この仮定に問題はないのは明らかである。もし議論のいずれかの段階で仮定が満たされないなら、定理の正しさを認めることになる。

ここまでの議論と §43 の議論を組み合わせれば任意の閉曲線 \(\bm{\gamma}\) について、\(\bm{\gamma}\) 内部の \(\bm{Z = 0}\) の根の数 (重根は別に数える) を \(\bm{k}\) とすれば、\(\bm{z}\) が \(\bm{\gamma}\) とたどるときの \(\bm{\arg Z}\) の増分は \(\bm{2k\pi}\) となることが示せる。これは読者への練習問題とする。

異なる方法を使った証明もあり、こちらが説明される場合も多い。ただしこの証明には §102 などの結果を二つ以上の変数の関数に拡張したものが必要となる。

§102 と同じように、\((x, y)\) 平面の任意の領域に含まれる任意の点に対応する \(x\) と \(y\) を考えたときの関数 \(f(x, y)\) の上限と下限を定義する。このとき §102 と同様に、連続関数 \(f(x, y)\) は任意の閉領域において上限と下限を取ることが示せる。

関数 \[ |Z| = |P(x + iy)| \] は常に正な \(x\) と \(y\) に関する連続関数である。\(\gamma\) の上および内部における下限を \(m\) とすると、ある \(z_{0}\) で \(|Z| = m\) となり、この値が \(|Z|\) の最小値となる。このときもし \(m = 0\) なら \(P(z_{0}) = 0\) となって証明すべきことが示される。よって \(m \gt 0\) と仮定する。

点 \(z_{0}\) は \(\gamma\) の内部または境界上にある。しかしもし \(\gamma\) が原点を中心とする半径 \(R\) の円で \(R\) が十分大きいなら、\(|z| \to \infty\) のとき \(|P(z)| \to \infty\) より後者の可能性は排除される。よって \(z_{0}\) は \(\gamma\) の内部にあると仮定できる。

\(z = z_{0} + \zeta\) として \(P(z)\) を \(\zeta\) のべきで整理して得られる式を \[ P(z) = P(z_{0}) + A_{1}\zeta + A_{2}\zeta^{2} + \cdots + A_{n}\zeta^{n} \] とする。\(A_{k}\) を \(0\) でない最初の係数として \(|A_{k}| = \mu\) および \(|\zeta| = \rho\) とする。\(\rho\) を十分小さく取れば \[ |A_{k+1}|\rho + |A_{k+2}|\rho^{2} + \cdots + |A_{n}|\rho^{n-k} \lt \dfrac{1}{2}\mu \] となる。このとき \[ |P(z) - P(z_{0}) - A_{k}\zeta^{k}| \lt \dfrac{1}{2}\mu\rho^{k} \] すなわち \[ |P(z)| \lt |P(z_{0}) + A_{k}\zeta^{k}| + \dfrac{1}{2}\mu\rho^{k} \] が成り立つ。

\(z\) が \(z_{0}\) を中心とする半径 \(\rho\) の円周上を動くとする。このとき \[ P(z_{0}) + A_{k}\zeta^{k} \] は中心が \(P(z_{0})\) で半径 \(|A_{k}\zeta^{k}| = \mu\rho^{k}\) の円周上を \(k\) 回周回し、原点と \(P(z_{0})\) を結ぶ直線とこの円の交点を \(k\) 回横切る。よって \(z\) が動く円周上には \(|P(z_{0}) + A_{k}\zeta^{k}| = |P(z_{0})| - \mu\rho^{k}\) を満たす点が \(k\) 個存在する。つまりこの点で \[ |P(z)| \lt |P(z_{0})| - \mu\rho^{k} + \dfrac{1}{2}\mu\rho^{k} = m - \dfrac{1}{2}\mu\rho^{k} \lt m \] が成り立つ。しかしこれは \(m\) が \(|P(z)|\) の下限であるという仮定と矛盾する。

したがって \(m\) は \(0\) であり、\(P(z_{0}) = 0\) が成り立つ。

1. ここで \(\Gamma\) が原点を通らない仮定を使っている。^[return]

2. 分割に使う平行な直線の構築方法を具体的に決めるのは難しくない。一番簡単なのは正および負の整数 \(k\) に対して \(x = k\delta_{1}\) と \(y = k\delta_{1}\) という直線を引くものである。^[return]

3. 例えば \(\delta_{m} = \delta_{1}/2^{m-1}\) とする。^[return]